26.1.2 反比例函数的图象和性质(第1课时) 课件(22张ppt)
文档属性
| 名称 | 26.1.2 反比例函数的图象和性质(第1课时) 课件(22张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-23 07:24:45 | ||
图片预览






文档简介
人教版数学九年级下册
第26.1.2 反比例函数的图象和性质(第1课时)
学习目标
1.经历画反比例函数的图象、归纳得到反比例函数的图象特征和性质的过程.
2.会画反比例函数图象,了解和掌握反比例函数的图象和性质.
3.能够初步应用反比例函数的图象和性质解题.
1.什么是反比例函数?
一般地,形如 (k 为常数,k≠0)的函数叫做反比例函数,其中x 是自变量,y是函数.自变量x的取值范围是不等于0的一切实数.
复习引入
2.反比例函数三种表达方式
y=kx-1
xy=k
复习引入
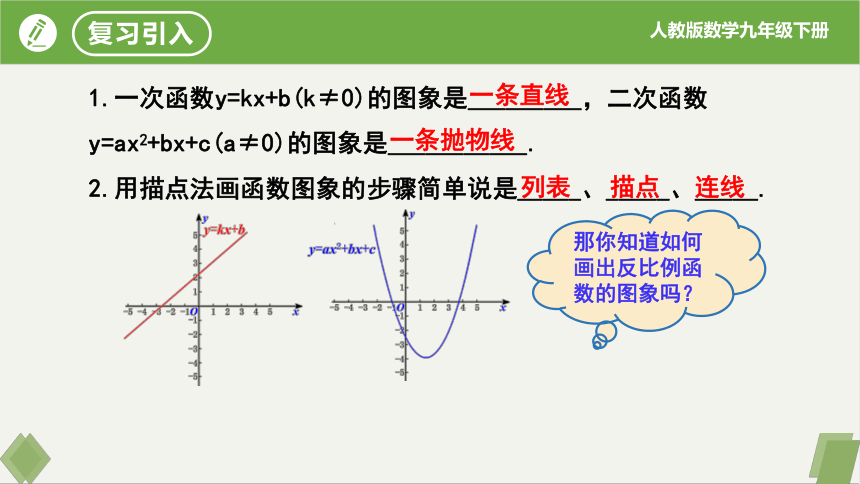
1.一次函数y=kx+b(k≠0)的图象是_________,二次函数y=ax2+bx+c(a≠0)的图象是___________.
2.用描点法画函数图象的步骤简单说是_____、_____、_____.
一条直线
一条抛物线
列表
描点
连线
那你知道如何画出反比例函数的图象吗?
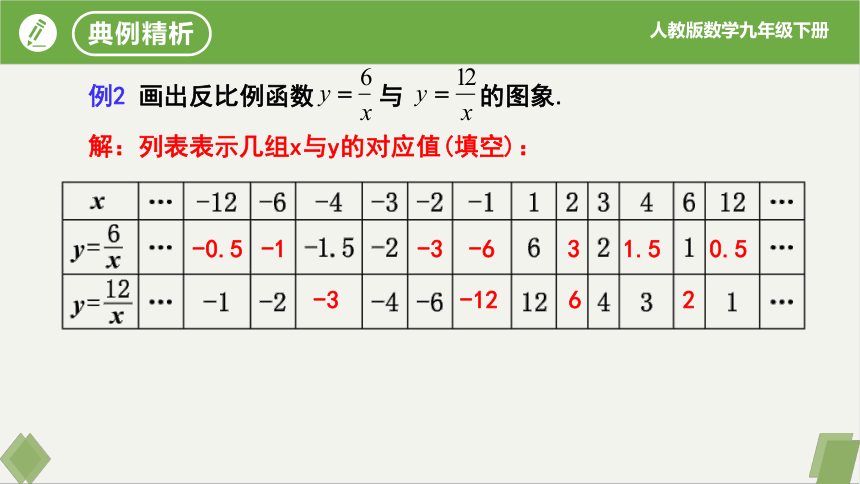
例2 画出反比例函数 与 的图象.
解:列表表示几组x与y的对应值(填空):
-0.5
-1
-3
-3
-6
-12
3
6
1.5
2
0.5
典例精析
-6
-5
-6
O
-2
5
6
x
y
4
3
2
1
1
2
3
4
5
6
-3
-4
-1
-5
-6
-1
-2
-3
-4
-5
-6
O
-2
5
6
x
y
4
3
2
1
1
2
3
4
5
6
-3
-4
-1
-1
-2
-3
-4
-5
典例精析
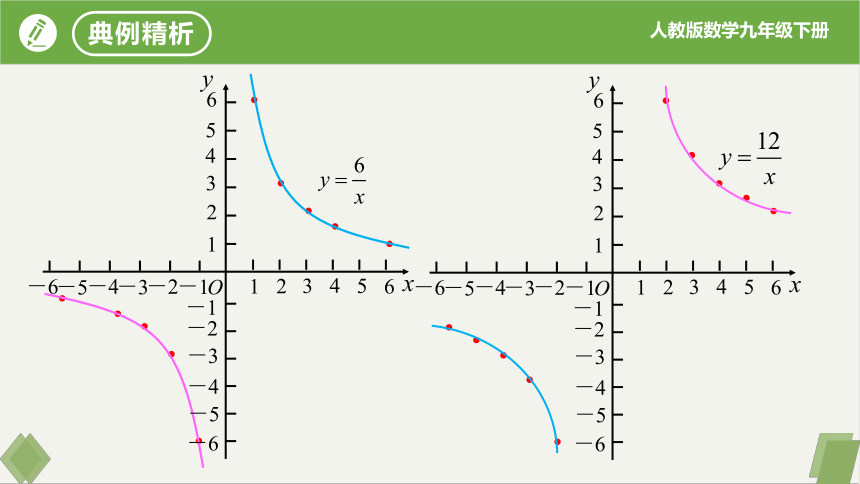
思考 观察这两个函数图象,回答问题:
(1)每个函数图象分别位于哪些象限?
(2)在每一个象限内,随着x的增大,y如何变化?你能由它们的解析式说明理由吗?
互动新授
函数图象分别位于第一、第三象限.
在每一个象限内,y随x的增大而减小.
互动新授
思考 观察这两个函数图象,回答问题:
(3)对于反比例函数 (k>0),考虑问题(1)(2),你能得出同样的结论吗?
一般地,当k>0时,对于反比例函数 ,由函数图象,并结合解析式,我们可以发现:
(1)函数图象分别位于第一、第三象限;
(2)在每一个象限内,y随x的增大而减小.
互动新授
探究 回顾前面我们利用函数图象,从特殊到一般研究反比例函数 (k>0)的性质的过程,你能用类似的方法研究反比例函数 (k<0)的图象和性质吗?
(1)函数图象分别位于第二、第四象限; ?
(2)在每一个象限内,y随x的增大而增大.
一般地,当k<0时,对于反比例函数 ,由函数图象,并结合解析式,我们可以发现:
互动新授
反比例函数的图象是由两条曲线组成,它是双曲线.
总结归纳
一般地,反比例函数的图象是双曲线,它具有以下性质:
(1)当k>0时,双曲线的两支分别位于第一、第三象限,在每一个象限内,y随x的增大而减小;
(2)当k<0时,双曲线的两支分别位于第二、第四象限,在每一个象限内,y随x的增大而增大.
1.若?????????
B
小试牛刀
2.已知点????????,????在反比例函数????=????????的图象上,其中a,k为常数,且????>????﹐则点M一定在(????)
A.第一象限 B.第二象限
C.第三象限 D.第四象限
?
A
小试牛刀
1.已知反比例函数y=4?kx
(1)若函数的图象位于第一、三象限,则k______;
(2)若在每一象限内,y随x增大而增大,则k______.
?
<4
>4
课堂检测
2.(1)已知点A(-2,y1),B(-1,y2),C(3,y3)都在反比例函数的图象上,比较y1、 y2 、y3的大小关系?
(2)如果点A(-2,y1),B(-1,y2)和C(3,y3)都在反比例函数的图象上,那么y1、 y2 、y3的大小关系又如何呢?
解:(1)∵k=4>0,
∴图象在第一、三象限内,每一象限内y随x的增大而减小
∵x10,
∴点A(-2,y1),点B(-1,y2)在第三象限,点C(3,y3)在第一象限.
∴y3>0, y2 (2)需分情况讨论k的正负:
①当k>0时, y2< y1< y3
②当k<0时, y3< y1< y2
课堂检测
1.如图26. 1-4,它是反比例函数 图象的一支.根据图象,回答下列问题:
(1)图象的另一支位于哪个象限?常数m 的取值范围是什么?
(2)在这个函数图象的某一支上任取点A (x1,y1)和点B (x2,y2).如果x1>x2,那么y1和y2有怎样的大小关系?
拓展训练
解:(1)反比例函数的图象只有两种可能:位于第一、第三象限,或者位于第二、第四象限.因为这个函数 的图象的一支位于第一象限,所以另一支必位于 第三象限.因为这个函数的图象位于第一、第三象限,所以m-5>0,解得 m>5.
(2)因为m-5>0。所以在这个函数图象的任一支上,y 都随x 的增大而减小,因此当x1>x2时,y1<y2.
拓展训练
2.已知 点 (a-1,y1),(a+1,y2)在反比例函数 (k>0)的图象上,若y1<y2,求a的取值范围.
解:由题意知,在图象的每一支上,y随x的增大而减小.
①当这两点在图象的同一支上时,
∵y1<y2,∴a-1>a+1, 无解;
②当这两点分别位于图象的两支上时,
∵y1<y2,∴必有y1<0<y2.
∴a-1<0,a+1>0, 解得:-1<a<1.
故a的取值范围为:-1<a<1.
拓展训练
{5940675A-B579-460E-94D1-54222C63F5DA}
比例系数
图象
图象形状
经过象限
增减性
y=
k>0
k<0
双曲线
第一、三象限
第二、四象限
y随x的增大而减小
y随x的增大而增大
课堂小结
1.关于反比例函数 下列说法正确的是( )
A.图象过点(2,-8)
B.图象在第一、三象限
C.当x>0时,y 随x 的增大而减小
D.当x<0时,y 随x 的增大而增大
2.点A (1,y1),B (3,y2)是反比例函数 图象上的两点,则y1,y2的大小关系是( )
A.y1>y2 B.y1=y2
C.y1<y2 D.不能确定
D
A
课后作业
3.若直线y=k1x(k1≠0)和双曲线y=????????????(k2≠0)在同一直X角坐标系内无交点,则k1与k2的关系是_________.
4.已知点A(a, y1),B(a+1, y2)在反比例函数y=????????+????????(m是常数)的图象上,且y1?
k1k2<0
-1课后作业
谢谢聆听
第26.1.2 反比例函数的图象和性质(第1课时)
学习目标
1.经历画反比例函数的图象、归纳得到反比例函数的图象特征和性质的过程.
2.会画反比例函数图象,了解和掌握反比例函数的图象和性质.
3.能够初步应用反比例函数的图象和性质解题.
1.什么是反比例函数?
一般地,形如 (k 为常数,k≠0)的函数叫做反比例函数,其中x 是自变量,y是函数.自变量x的取值范围是不等于0的一切实数.
复习引入
2.反比例函数三种表达方式
y=kx-1
xy=k
复习引入
1.一次函数y=kx+b(k≠0)的图象是_________,二次函数y=ax2+bx+c(a≠0)的图象是___________.
2.用描点法画函数图象的步骤简单说是_____、_____、_____.
一条直线
一条抛物线
列表
描点
连线
那你知道如何画出反比例函数的图象吗?
例2 画出反比例函数 与 的图象.
解:列表表示几组x与y的对应值(填空):
-0.5
-1
-3
-3
-6
-12
3
6
1.5
2
0.5
典例精析
-6
-5
-6
O
-2
5
6
x
y
4
3
2
1
1
2
3
4
5
6
-3
-4
-1
-5
-6
-1
-2
-3
-4
-5
-6
O
-2
5
6
x
y
4
3
2
1
1
2
3
4
5
6
-3
-4
-1
-1
-2
-3
-4
-5
典例精析
思考 观察这两个函数图象,回答问题:
(1)每个函数图象分别位于哪些象限?
(2)在每一个象限内,随着x的增大,y如何变化?你能由它们的解析式说明理由吗?
互动新授
函数图象分别位于第一、第三象限.
在每一个象限内,y随x的增大而减小.
互动新授
思考 观察这两个函数图象,回答问题:
(3)对于反比例函数 (k>0),考虑问题(1)(2),你能得出同样的结论吗?
一般地,当k>0时,对于反比例函数 ,由函数图象,并结合解析式,我们可以发现:
(1)函数图象分别位于第一、第三象限;
(2)在每一个象限内,y随x的增大而减小.
互动新授
探究 回顾前面我们利用函数图象,从特殊到一般研究反比例函数 (k>0)的性质的过程,你能用类似的方法研究反比例函数 (k<0)的图象和性质吗?
(1)函数图象分别位于第二、第四象限; ?
(2)在每一个象限内,y随x的增大而增大.
一般地,当k<0时,对于反比例函数 ,由函数图象,并结合解析式,我们可以发现:
互动新授
反比例函数的图象是由两条曲线组成,它是双曲线.
总结归纳
一般地,反比例函数的图象是双曲线,它具有以下性质:
(1)当k>0时,双曲线的两支分别位于第一、第三象限,在每一个象限内,y随x的增大而减小;
(2)当k<0时,双曲线的两支分别位于第二、第四象限,在每一个象限内,y随x的增大而增大.
1.若?????????
B
小试牛刀
2.已知点????????,????在反比例函数????=????????的图象上,其中a,k为常数,且????>????﹐则点M一定在(????)
A.第一象限 B.第二象限
C.第三象限 D.第四象限
?
A
小试牛刀
1.已知反比例函数y=4?kx
(1)若函数的图象位于第一、三象限,则k______;
(2)若在每一象限内,y随x增大而增大,则k______.
?
<4
>4
课堂检测
2.(1)已知点A(-2,y1),B(-1,y2),C(3,y3)都在反比例函数的图象上,比较y1、 y2 、y3的大小关系?
(2)如果点A(-2,y1),B(-1,y2)和C(3,y3)都在反比例函数的图象上,那么y1、 y2 、y3的大小关系又如何呢?
解:(1)∵k=4>0,
∴图象在第一、三象限内,每一象限内y随x的增大而减小
∵x1
∴点A(-2,y1),点B(-1,y2)在第三象限,点C(3,y3)在第一象限.
∴y3>0, y2
①当k>0时, y2< y1< y3
②当k<0时, y3< y1< y2
课堂检测
1.如图26. 1-4,它是反比例函数 图象的一支.根据图象,回答下列问题:
(1)图象的另一支位于哪个象限?常数m 的取值范围是什么?
(2)在这个函数图象的某一支上任取点A (x1,y1)和点B (x2,y2).如果x1>x2,那么y1和y2有怎样的大小关系?
拓展训练
解:(1)反比例函数的图象只有两种可能:位于第一、第三象限,或者位于第二、第四象限.因为这个函数 的图象的一支位于第一象限,所以另一支必位于 第三象限.因为这个函数的图象位于第一、第三象限,所以m-5>0,解得 m>5.
(2)因为m-5>0。所以在这个函数图象的任一支上,y 都随x 的增大而减小,因此当x1>x2时,y1<y2.
拓展训练
2.已知 点 (a-1,y1),(a+1,y2)在反比例函数 (k>0)的图象上,若y1<y2,求a的取值范围.
解:由题意知,在图象的每一支上,y随x的增大而减小.
①当这两点在图象的同一支上时,
∵y1<y2,∴a-1>a+1, 无解;
②当这两点分别位于图象的两支上时,
∵y1<y2,∴必有y1<0<y2.
∴a-1<0,a+1>0, 解得:-1<a<1.
故a的取值范围为:-1<a<1.
拓展训练
{5940675A-B579-460E-94D1-54222C63F5DA}
比例系数
图象
图象形状
经过象限
增减性
y=
k>0
k<0
双曲线
第一、三象限
第二、四象限
y随x的增大而减小
y随x的增大而增大
课堂小结
1.关于反比例函数 下列说法正确的是( )
A.图象过点(2,-8)
B.图象在第一、三象限
C.当x>0时,y 随x 的增大而减小
D.当x<0时,y 随x 的增大而增大
2.点A (1,y1),B (3,y2)是反比例函数 图象上的两点,则y1,y2的大小关系是( )
A.y1>y2 B.y1=y2
C.y1<y2 D.不能确定
D
A
课后作业
3.若直线y=k1x(k1≠0)和双曲线y=????????????(k2≠0)在同一直X角坐标系内无交点,则k1与k2的关系是_________.
4.已知点A(a, y1),B(a+1, y2)在反比例函数y=????????+????????(m是常数)的图象上,且y1
k1k2<0
-1
谢谢聆听
