九年级专题复习----《圆》(含答案)
文档属性
| 名称 | 九年级专题复习----《圆》(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 215.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-11 06:43:13 | ||
图片预览


文档简介
九年级专题复习----《圆》
一.选择题(共14小题)
1.(2014 毕节市)如图,已知⊙O的半径为13,弦AB长为24,则点O到AB的距离是( )
( http: / / www.21cnjy.com )
A. 6 B. 5 C. 4 D. 3
2.(2014 牡丹江)如图,⊙O的直径AB=2,弦AC=1,点D在⊙O上,则∠D的度数是( )
( http: / / www.21cnjy.com )
A. 30° B. 45° C. 60° D. 75°
3.(2014 益阳)如图,在平面直角坐 ( http: / / www.21cnjy.com )标系xOy中,半径为2的⊙P的圆心P的坐标为(﹣3,0),将⊙P沿x轴正方向平移,使⊙P与y轴相切,则平移的距离为( )
( http: / / www.21cnjy.com )
A. 1 B. 1或5 C. 3 D. 5
4.(2015 宝山区一模)已知⊙O半径为3,M为直线AB上一点,若MO=3,则直线AB与⊙O的位置关系为( )
A. 相切 B. 相交 C. 相切或相离 D. 相切或相交
5.(2014 贵港)如图,AB是⊙O的直径,==,∠COD=34°,则∠AEO的度数是( )
( http: / / www.21cnjy.com )
A. 51° B. 56° C. 68° D. 78°
6.(2014 凉山州)已知⊙O的直径CD=10cm,AB是⊙O的弦,AB=8cm,且AB⊥CD,垂足为M,则AC的长为( )
A. cm B. cm C. cm或cm D. cm或cm
7.(2014 济南)如图,⊙O的半径为1,△ABC是⊙O的内接等边三角形,点D、E在圆上,四边形BCDE为矩形,这个矩形的面积是( )
( http: / / www.21cnjy.com )
A. 2 B. C. D.
8.(2014 珠海)如图,线段AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠AOD等于( )
( http: / / www.21cnjy.com )
A. 160° B. 150° C. 140° D. 120°
9.(2014 无锡)如图,AB是⊙O的直 ( http: / / www.21cnjy.com )径,CD是⊙O的切线,切点为D,CD与AB的延长线交于点C,∠A=30°,给出下面3个结论:①AD=CD;②BD=BC;③AB=2BC,其中正确结论的个数是( )
( http: / / www.21cnjy.com )
A. 3 B. 2 C. 1 D. 0
10.(2014 义乌市)一张圆心角为45 ( http: / / www.21cnjy.com )°的扇形纸板和圆形纸板按如图方式分别剪成一个正方形,边长都为1,则扇形和圆形纸板的面积比是( )
( http: / / www.21cnjy.com )
A. 5:4 B. 5:2 C. :2 D. :
11.(2014 莱芜)如图,在正五边形ABCDE中,连接AC、AD、CE,CE交AD于点F,连接BF,下列说法不正确的是( )
( http: / / www.21cnjy.com )
A. △CDF的周长等于AD+CD B. FC平分∠BFD
C. AC2+BF2=4CD2 D. DE2=EF CE
12.(2014 海南)一个圆锥的侧面展开图形是半径为8cm,圆心角为120°的扇形,则此圆锥的底面半径为( )
A. cm B. cm C. 3cm D. cm
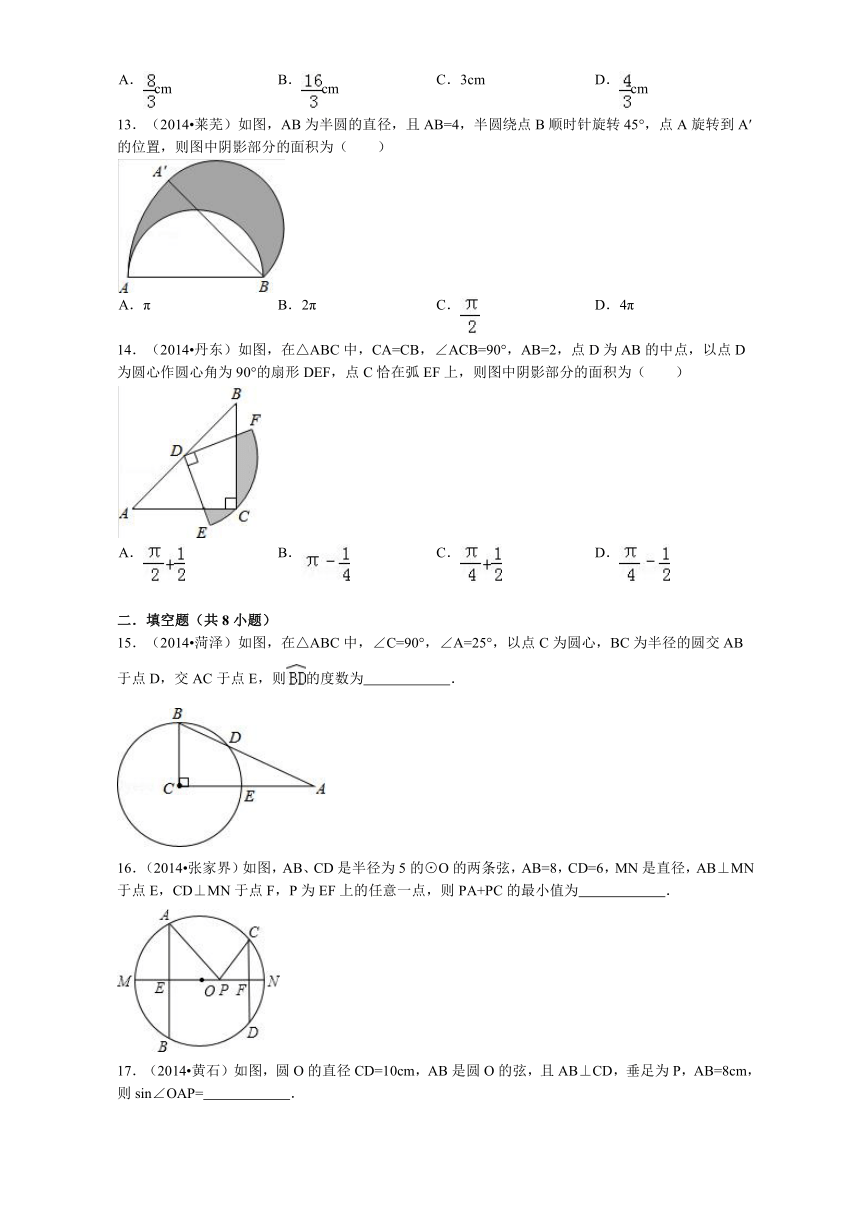
13.(2014 莱芜)如 ( http: / / www.21cnjy.com )图,AB为半圆的直径,且AB=4,半圆绕点B顺时针旋转45°,点A旋转到A′的位置,则图中阴影部分的面积为( )
( http: / / www.21cnjy.com )
A. π B. 2π C. D. 4π
14.(2014 丹东)如图,在△AB ( http: / / www.21cnjy.com )C中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为( )
( http: / / www.21cnjy.com )
A. B. C. D.
二.填空题(共8小题)
15.(2014 菏泽)如图,在△ABC中,∠C=90°,∠A=25°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,则的度数为 .
( http: / / www.21cnjy.com )
16.(2014 张家界)如图,A ( http: / / www.21cnjy.com )B、CD是半径为5的⊙O的两条弦,AB=8,CD=6,MN是直径,AB⊥MN于点E,CD⊥MN于点F,P为EF上的任意一点,则PA+PC的最小值为 .
( http: / / www.21cnjy.com )
17.(2014 黄石)如图,圆O ( http: / / www.21cnjy.com )的直径CD=10cm,AB是圆O的弦,且AB⊥CD,垂足为P,AB=8cm,则sin∠OAP= .
( http: / / www.21cnjy.com )
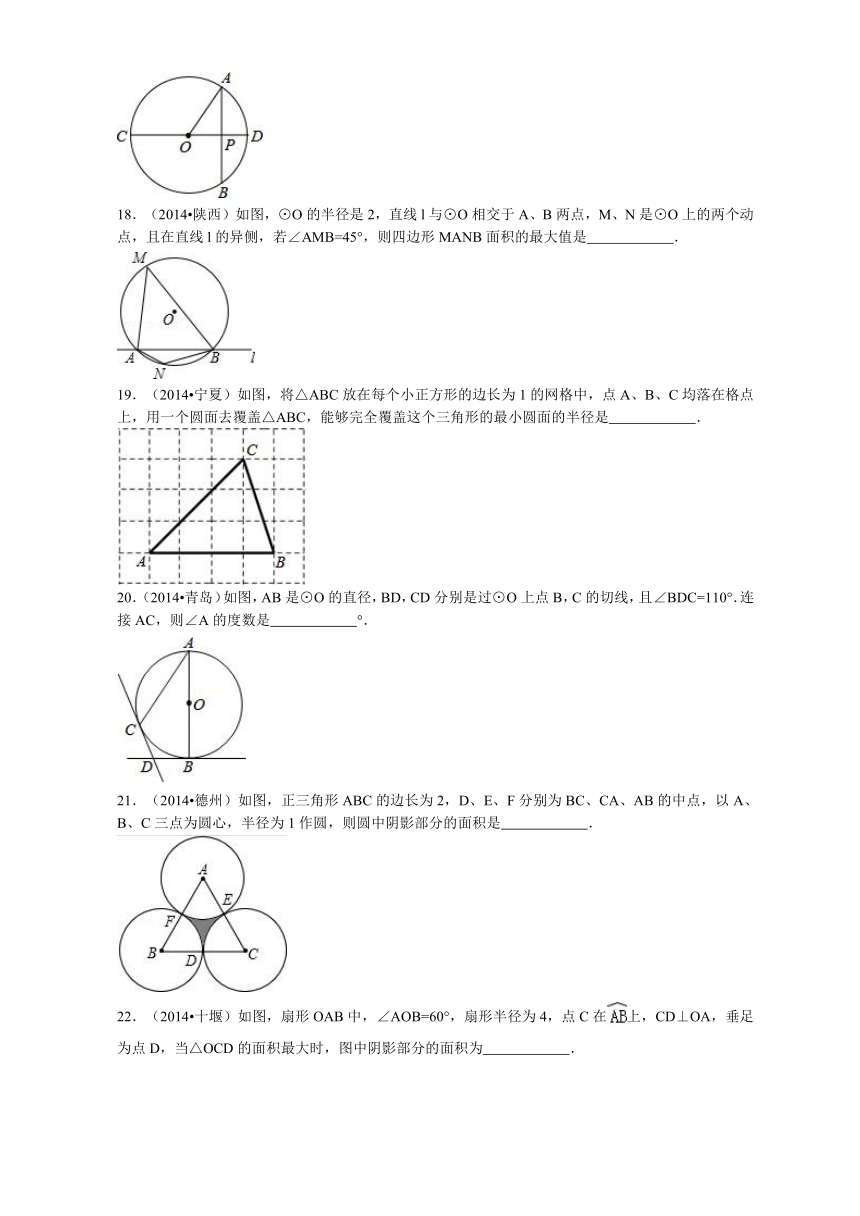
18.(2014 陕西)如图,⊙O的半径是2 ( http: / / www.21cnjy.com ),直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是 .
( http: / / www.21cnjy.com )
19.(2014 宁夏)如 ( http: / / www.21cnjy.com )图,将△ABC放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上,用一个圆面去覆盖△ABC,能够完全覆盖这个三角形的最小圆面的半径是 .
( http: / / www.21cnjy.com )
20.(2014 青岛) ( http: / / www.21cnjy.com )如图,AB是⊙O的直径,BD,CD分别是过⊙O上点B,C的切线,且∠BDC=110°.连接AC,则∠A的度数是 °.
( http: / / www.21cnjy.com )
21.(2014 德州)如图,正三角形 ( http: / / www.21cnjy.com )ABC的边长为2,D、E、F分别为BC、CA、AB的中点,以A、B、C三点为圆心,半径为1作圆,则圆中阴影部分的面积是 .
( http: / / www.21cnjy.com )
22.(2014 十堰)如图,扇形OAB中,∠AOB=60°,扇形半径为4,点C在上,CD⊥OA,垂足为点D,当△OCD的面积最大时,图中阴影部分的面积为 .
( http: / / www.21cnjy.com )
三.解答题(共6小题)
23.(2014 滨州)如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.
( http: / / www.21cnjy.com )
24.(2014 南通)如图,AB是⊙O的直径,弦CD⊥AB于点E,点M在⊙O上,MD恰好经过圆心O,连接MB.
(1)若CD=16,BE=4,求⊙O的直径;
(2)若∠M=∠D,求∠D的度数.
( http: / / www.21cnjy.com )
25.(2014 大庆)如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,PB与CD交于点F,∠PBC=∠C.
(1)求证:CB∥PD;
(2)若∠PBC=22.5°,⊙O的半径R=2,求劣弧AC的长度.
( http: / / www.21cnjy.com )
26.(2014 呼和浩特)如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线CM.
(1)求证:∠ACM=∠ABC;
(2)延长BC到D,使BC=CD,连接AD与CM交于点E,若⊙O的半径为3,ED=2,求△ACE的外接圆的半径.
( http: / / www.21cnjy.com )
27.(2014 咸宁)如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AD⊥CD于点D.
(1)求证:AC平分∠DAB;
(2)若点E为的中点,AD=,AC=8,求AB和CE的长.
( http: / / www.21cnjy.com )
28.(2014 黔东南州)已知:AB是⊙O的直径,直线CP切⊙O于点C,过点B作BD⊥CP于D.
(1)求证:△ACB∽△CDB;
(2)若⊙O的半径为1,∠BCP=30°,求图中阴影部分的面积.
( http: / / www.21cnjy.com )
参考答案与试题解析
一.选择题(共14小题)
1. B.2. C.3. B.4. D.5. A.6. C.7. B.8. C.9. A.10. A.11. B.
12. A.13. B.14.D
二.填空题(共8小题)
15. 50°. 16. 17. . 18. 4. 19. . 20. 35.
21. ﹣. 22. 2π﹣4.
三.解答题(共6小题)
23.(1)证明:连接OC.
∵AC=CD,∠ACD=120°,∴∠A=∠D=30°.
∵OA=OC,∴∠2=∠A=30°.
∴∠OCD=180°﹣∠A﹣∠D﹣∠2=90°.∴CD是⊙O的切线.
(2)解:∵∠A=30°,∴∠1=2∠A=60°.∴S扇形BOC=.
在Rt△OCD中,
∵,∴.∴.∴图中阴影部分的面积为:.
( http: / / www.21cnjy.com )
24.解:(1)∵AB⊥CD,CD=16,∴CE=DE=8,
设OB=x,
又∵BE=4,∴x2=(x﹣4)2+82,解得:x=10,∴⊙O的直径是20.
(2)∵∠M=∠BOD,∠M=∠D,∴∠D=∠BOD,
∵AB⊥CD,∴∠D=30°.
25.解:(1)∵∠PBC=∠D,∠PBC=∠C,∴∠C=∠D,∴CB∥PD;
(2)连结OC,OD.
∵AB是⊙O的直径,弦CD⊥AB于点E,∴=,
∵∠PBC=∠DCB=22.5°,∴∠BOC=∠BOD=2∠C=45°,∴∠AOC=180°﹣∠BOC=135°,∴劣弧AC的长为:=.
( http: / / www.21cnjy.com )
26.(1)证明:如图,连接OC,
( http: / / www.21cnjy.com )
∵AB为⊙O的直径,∴∠ACB=90°,∴∠ABC+∠BAC=90°,
又∵CM是⊙O的切线,∴OC⊥CM,∴∠ACM+∠ACO=90°,
∵CO=AO,∴∠BAC=∠ACO,∴∠ACM=∠ABC;
(2)解:∵BC=CD,∠ACB=90°,∴∠OAC=∠CAD,
∵OA=OC,∴∠OAC=∠OCA,∴∠OCA=∠CAD,∴OC∥AD,
又∵OC⊥CE,∴AD⊥CE,∴△AEC是直角三角形,∴△AEC的外接圆的直径是AC,
又∵∠ABC+∠BAC=90°,∠ACM+∠ECD=90°,∴△ABC∽△CDE,∴=,
⊙O的半径为3,∴AB=6,∴=,∴BC2=12,∴BC=2,∴AC==2,∴△AEC的外接圆的半径为.
27.(1)证明:连接OC,
∵直线CD与⊙O相切于点C,∴OC⊥CD,
∵AD⊥CD,∴OC∥AD,∴∠DAC=∠OCA,
∵OA=OC,∴∠OCA=∠OAC,∴∠OAC=∠DAC,即AC平分∠DAB;
(2)连接BC,OE,过点A作AF⊥EC于点F,
∵AB是⊙O的直径,∴∠ACB=90°,∴∠ACB=∠ADC,
∵∠DAC=∠BAC,∴△ADC∽△ACB,∴,即,解得:AB=10,∴BC==6,
∵点E为的中点,∴∠AOE=90°,∴OE=OA=AB=5,∴AE==5,
∵∠AEF=∠B(同弧所对圆周角相等),∠AFE=∠ACB=90°,∴△ACB∽△AFE,
∴,∴,∴AF=4,EF=3,
∵∠ACF=∠AOE=45°,∴△ACF是等腰直角三角形,∴CF=AF=4,∴CE=CF+EF=7.
( http: / / www.21cnjy.com )
28.(1)证明:如图,连接OC,
( http: / / www.21cnjy.com )
∵直线CP是⊙O的切线,∴∠BCD+∠OCB=90°,
∵AB是直径,∴∠ACB=90°,∴∠ACO+∠OCB=90°∴∠BCD=∠ACO,
又∵∠BAC=∠ACO,∴∠BCD=∠BAC,
又∵BD⊥CP∴∠CDB=90°,∴∠ACB=∠CDB=90°∴△ACB∽△CDB;
(2)解:如图,连接OC,
( http: / / www.21cnjy.com )
∵直线CP是⊙O的切线,∠BCP=30°,∴∠COB=2∠BCP=60°,∴△OCB是正三角形,
∵⊙O的半径为1,∴S△OCB=,S扇形OCB==π,
故阴影部分的面积=S扇形OCB﹣S△OCB=π﹣.
一.选择题(共14小题)
1.(2014 毕节市)如图,已知⊙O的半径为13,弦AB长为24,则点O到AB的距离是( )
( http: / / www.21cnjy.com )
A. 6 B. 5 C. 4 D. 3
2.(2014 牡丹江)如图,⊙O的直径AB=2,弦AC=1,点D在⊙O上,则∠D的度数是( )
( http: / / www.21cnjy.com )
A. 30° B. 45° C. 60° D. 75°
3.(2014 益阳)如图,在平面直角坐 ( http: / / www.21cnjy.com )标系xOy中,半径为2的⊙P的圆心P的坐标为(﹣3,0),将⊙P沿x轴正方向平移,使⊙P与y轴相切,则平移的距离为( )
( http: / / www.21cnjy.com )
A. 1 B. 1或5 C. 3 D. 5
4.(2015 宝山区一模)已知⊙O半径为3,M为直线AB上一点,若MO=3,则直线AB与⊙O的位置关系为( )
A. 相切 B. 相交 C. 相切或相离 D. 相切或相交
5.(2014 贵港)如图,AB是⊙O的直径,==,∠COD=34°,则∠AEO的度数是( )
( http: / / www.21cnjy.com )
A. 51° B. 56° C. 68° D. 78°
6.(2014 凉山州)已知⊙O的直径CD=10cm,AB是⊙O的弦,AB=8cm,且AB⊥CD,垂足为M,则AC的长为( )
A. cm B. cm C. cm或cm D. cm或cm
7.(2014 济南)如图,⊙O的半径为1,△ABC是⊙O的内接等边三角形,点D、E在圆上,四边形BCDE为矩形,这个矩形的面积是( )
( http: / / www.21cnjy.com )
A. 2 B. C. D.
8.(2014 珠海)如图,线段AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠AOD等于( )
( http: / / www.21cnjy.com )
A. 160° B. 150° C. 140° D. 120°
9.(2014 无锡)如图,AB是⊙O的直 ( http: / / www.21cnjy.com )径,CD是⊙O的切线,切点为D,CD与AB的延长线交于点C,∠A=30°,给出下面3个结论:①AD=CD;②BD=BC;③AB=2BC,其中正确结论的个数是( )
( http: / / www.21cnjy.com )
A. 3 B. 2 C. 1 D. 0
10.(2014 义乌市)一张圆心角为45 ( http: / / www.21cnjy.com )°的扇形纸板和圆形纸板按如图方式分别剪成一个正方形,边长都为1,则扇形和圆形纸板的面积比是( )
( http: / / www.21cnjy.com )
A. 5:4 B. 5:2 C. :2 D. :
11.(2014 莱芜)如图,在正五边形ABCDE中,连接AC、AD、CE,CE交AD于点F,连接BF,下列说法不正确的是( )
( http: / / www.21cnjy.com )
A. △CDF的周长等于AD+CD B. FC平分∠BFD
C. AC2+BF2=4CD2 D. DE2=EF CE
12.(2014 海南)一个圆锥的侧面展开图形是半径为8cm,圆心角为120°的扇形,则此圆锥的底面半径为( )
A. cm B. cm C. 3cm D. cm
13.(2014 莱芜)如 ( http: / / www.21cnjy.com )图,AB为半圆的直径,且AB=4,半圆绕点B顺时针旋转45°,点A旋转到A′的位置,则图中阴影部分的面积为( )
( http: / / www.21cnjy.com )
A. π B. 2π C. D. 4π
14.(2014 丹东)如图,在△AB ( http: / / www.21cnjy.com )C中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为( )
( http: / / www.21cnjy.com )
A. B. C. D.
二.填空题(共8小题)
15.(2014 菏泽)如图,在△ABC中,∠C=90°,∠A=25°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,则的度数为 .
( http: / / www.21cnjy.com )
16.(2014 张家界)如图,A ( http: / / www.21cnjy.com )B、CD是半径为5的⊙O的两条弦,AB=8,CD=6,MN是直径,AB⊥MN于点E,CD⊥MN于点F,P为EF上的任意一点,则PA+PC的最小值为 .
( http: / / www.21cnjy.com )
17.(2014 黄石)如图,圆O ( http: / / www.21cnjy.com )的直径CD=10cm,AB是圆O的弦,且AB⊥CD,垂足为P,AB=8cm,则sin∠OAP= .
( http: / / www.21cnjy.com )
18.(2014 陕西)如图,⊙O的半径是2 ( http: / / www.21cnjy.com ),直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是 .
( http: / / www.21cnjy.com )
19.(2014 宁夏)如 ( http: / / www.21cnjy.com )图,将△ABC放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上,用一个圆面去覆盖△ABC,能够完全覆盖这个三角形的最小圆面的半径是 .
( http: / / www.21cnjy.com )
20.(2014 青岛) ( http: / / www.21cnjy.com )如图,AB是⊙O的直径,BD,CD分别是过⊙O上点B,C的切线,且∠BDC=110°.连接AC,则∠A的度数是 °.
( http: / / www.21cnjy.com )
21.(2014 德州)如图,正三角形 ( http: / / www.21cnjy.com )ABC的边长为2,D、E、F分别为BC、CA、AB的中点,以A、B、C三点为圆心,半径为1作圆,则圆中阴影部分的面积是 .
( http: / / www.21cnjy.com )
22.(2014 十堰)如图,扇形OAB中,∠AOB=60°,扇形半径为4,点C在上,CD⊥OA,垂足为点D,当△OCD的面积最大时,图中阴影部分的面积为 .
( http: / / www.21cnjy.com )
三.解答题(共6小题)
23.(2014 滨州)如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.
( http: / / www.21cnjy.com )
24.(2014 南通)如图,AB是⊙O的直径,弦CD⊥AB于点E,点M在⊙O上,MD恰好经过圆心O,连接MB.
(1)若CD=16,BE=4,求⊙O的直径;
(2)若∠M=∠D,求∠D的度数.
( http: / / www.21cnjy.com )
25.(2014 大庆)如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,PB与CD交于点F,∠PBC=∠C.
(1)求证:CB∥PD;
(2)若∠PBC=22.5°,⊙O的半径R=2,求劣弧AC的长度.
( http: / / www.21cnjy.com )
26.(2014 呼和浩特)如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线CM.
(1)求证:∠ACM=∠ABC;
(2)延长BC到D,使BC=CD,连接AD与CM交于点E,若⊙O的半径为3,ED=2,求△ACE的外接圆的半径.
( http: / / www.21cnjy.com )
27.(2014 咸宁)如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AD⊥CD于点D.
(1)求证:AC平分∠DAB;
(2)若点E为的中点,AD=,AC=8,求AB和CE的长.
( http: / / www.21cnjy.com )
28.(2014 黔东南州)已知:AB是⊙O的直径,直线CP切⊙O于点C,过点B作BD⊥CP于D.
(1)求证:△ACB∽△CDB;
(2)若⊙O的半径为1,∠BCP=30°,求图中阴影部分的面积.
( http: / / www.21cnjy.com )
参考答案与试题解析
一.选择题(共14小题)
1. B.2. C.3. B.4. D.5. A.6. C.7. B.8. C.9. A.10. A.11. B.
12. A.13. B.14.D
二.填空题(共8小题)
15. 50°. 16. 17. . 18. 4. 19. . 20. 35.
21. ﹣. 22. 2π﹣4.
三.解答题(共6小题)
23.(1)证明:连接OC.
∵AC=CD,∠ACD=120°,∴∠A=∠D=30°.
∵OA=OC,∴∠2=∠A=30°.
∴∠OCD=180°﹣∠A﹣∠D﹣∠2=90°.∴CD是⊙O的切线.
(2)解:∵∠A=30°,∴∠1=2∠A=60°.∴S扇形BOC=.
在Rt△OCD中,
∵,∴.∴.∴图中阴影部分的面积为:.
( http: / / www.21cnjy.com )
24.解:(1)∵AB⊥CD,CD=16,∴CE=DE=8,
设OB=x,
又∵BE=4,∴x2=(x﹣4)2+82,解得:x=10,∴⊙O的直径是20.
(2)∵∠M=∠BOD,∠M=∠D,∴∠D=∠BOD,
∵AB⊥CD,∴∠D=30°.
25.解:(1)∵∠PBC=∠D,∠PBC=∠C,∴∠C=∠D,∴CB∥PD;
(2)连结OC,OD.
∵AB是⊙O的直径,弦CD⊥AB于点E,∴=,
∵∠PBC=∠DCB=22.5°,∴∠BOC=∠BOD=2∠C=45°,∴∠AOC=180°﹣∠BOC=135°,∴劣弧AC的长为:=.
( http: / / www.21cnjy.com )
26.(1)证明:如图,连接OC,
( http: / / www.21cnjy.com )
∵AB为⊙O的直径,∴∠ACB=90°,∴∠ABC+∠BAC=90°,
又∵CM是⊙O的切线,∴OC⊥CM,∴∠ACM+∠ACO=90°,
∵CO=AO,∴∠BAC=∠ACO,∴∠ACM=∠ABC;
(2)解:∵BC=CD,∠ACB=90°,∴∠OAC=∠CAD,
∵OA=OC,∴∠OAC=∠OCA,∴∠OCA=∠CAD,∴OC∥AD,
又∵OC⊥CE,∴AD⊥CE,∴△AEC是直角三角形,∴△AEC的外接圆的直径是AC,
又∵∠ABC+∠BAC=90°,∠ACM+∠ECD=90°,∴△ABC∽△CDE,∴=,
⊙O的半径为3,∴AB=6,∴=,∴BC2=12,∴BC=2,∴AC==2,∴△AEC的外接圆的半径为.
27.(1)证明:连接OC,
∵直线CD与⊙O相切于点C,∴OC⊥CD,
∵AD⊥CD,∴OC∥AD,∴∠DAC=∠OCA,
∵OA=OC,∴∠OCA=∠OAC,∴∠OAC=∠DAC,即AC平分∠DAB;
(2)连接BC,OE,过点A作AF⊥EC于点F,
∵AB是⊙O的直径,∴∠ACB=90°,∴∠ACB=∠ADC,
∵∠DAC=∠BAC,∴△ADC∽△ACB,∴,即,解得:AB=10,∴BC==6,
∵点E为的中点,∴∠AOE=90°,∴OE=OA=AB=5,∴AE==5,
∵∠AEF=∠B(同弧所对圆周角相等),∠AFE=∠ACB=90°,∴△ACB∽△AFE,
∴,∴,∴AF=4,EF=3,
∵∠ACF=∠AOE=45°,∴△ACF是等腰直角三角形,∴CF=AF=4,∴CE=CF+EF=7.
( http: / / www.21cnjy.com )
28.(1)证明:如图,连接OC,
( http: / / www.21cnjy.com )
∵直线CP是⊙O的切线,∴∠BCD+∠OCB=90°,
∵AB是直径,∴∠ACB=90°,∴∠ACO+∠OCB=90°∴∠BCD=∠ACO,
又∵∠BAC=∠ACO,∴∠BCD=∠BAC,
又∵BD⊥CP∴∠CDB=90°,∴∠ACB=∠CDB=90°∴△ACB∽△CDB;
(2)解:如图,连接OC,
( http: / / www.21cnjy.com )
∵直线CP是⊙O的切线,∠BCP=30°,∴∠COB=2∠BCP=60°,∴△OCB是正三角形,
∵⊙O的半径为1,∴S△OCB=,S扇形OCB==π,
故阴影部分的面积=S扇形OCB﹣S△OCB=π﹣.
