七年级上册人教版数学第二章《整式的加减》能力提升检测卷(含解析)
文档属性
| 名称 | 七年级上册人教版数学第二章《整式的加减》能力提升检测卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 312.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-24 00:00:00 | ||
图片预览



文档简介
第二章整式的加减
能力提升检测卷
时间:90分钟满分:100分
一、选择题(共10小题,每小题3分,计30分.每小题只有一个选项是符合题意的)
1.下列各式:① a-b2,② y2,③ π-,④ ,⑤ 0,⑥ -x2+y-2z3.其中整式有()
A.3个 B.4个 C.5个 D.6个
2.某种型号的电脑的标价为m元,为促进销售,商场推出促销活动.若小明的爸爸购买这款电脑的付款金额为(90%m-200)元,则下列说法中,能正确表示促销活动的是( )
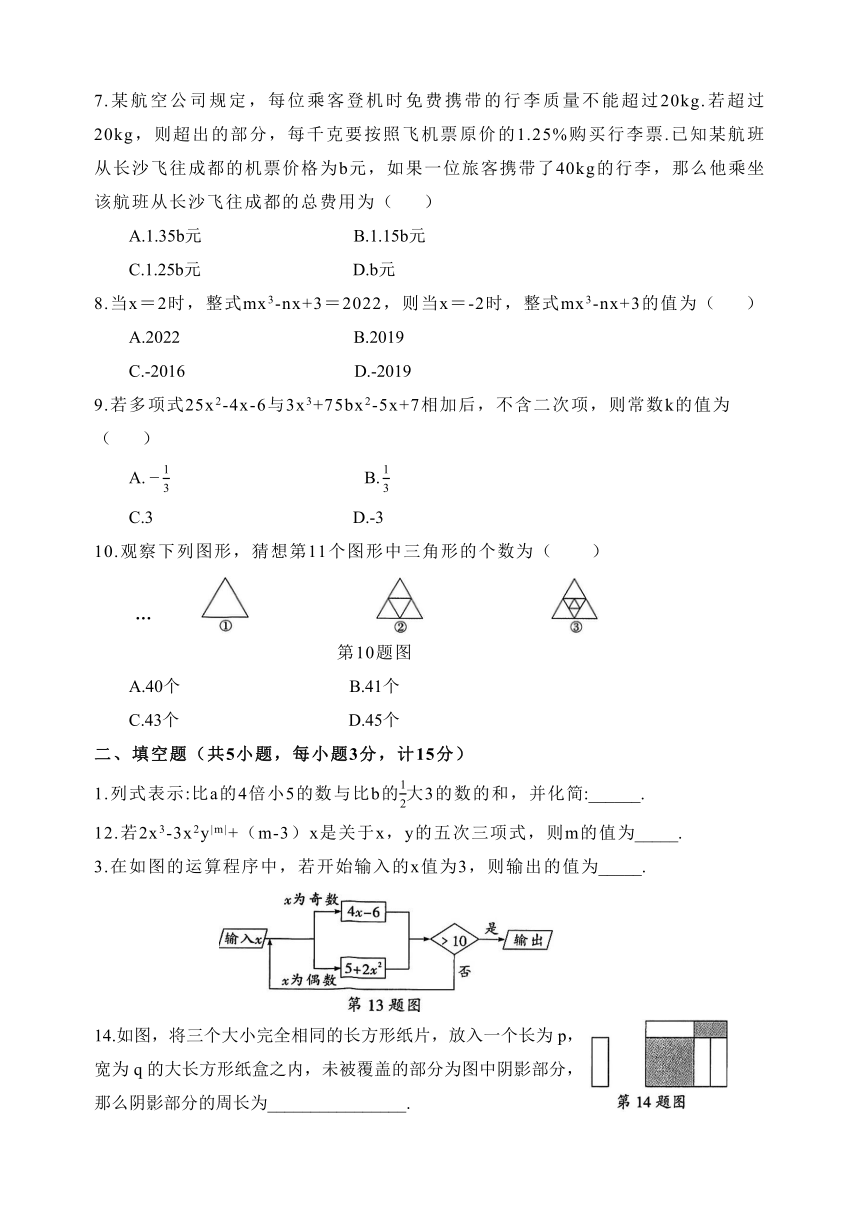
A.先在标价基础上打九折,再减200元
B.先在标价基础上减200元,再整体打九折
C.先在标价基础上打一折,再减200元
D.先在标价基础上减200元,再整体打一折
3.下列说法错误的是( )
的系数是 B.数字是单项式
C. -2m2n3与3n3m2是同类项 D.32x3y的次数是5
4.下列式子中,去括号正确的是( )
A.3a-(2a-b)=3a-2a-b
B.2a+2(-2a-3b)=2a-4a-6b
C.-3(a+6)=-3a-6
D.1-(a2+b2-1)=-a2-b2
5.若整式-(3x3ym-1)+3(xny+1)经过化简后的结果等于4,则m-n的值为( )
A.2 B.-2 C.4 D.-4
6.若M=2x2-6x+11,N=3x2-6x+12,则M和N的大小关系是( )
A. M>N B.M=N
C. M<N D无法确定
7.某航空公司规定,每位乘客登机时免费携带的行李质量不能超过20kg.若超过20kg,则超出的部分,每千克要按照飞机票原价的1.25%购买行李票.已知某航班从长沙飞往成都的机票价格为b元,如果一位旅客携带了40kg的行李,那么他乘坐该航班从长沙飞往成都的总费用为( )
A.1.35b元 B.1.15b元
C.1.25b元 D.b元
8.当x=2时,整式mx3-nx+3=2022,则当x=-2时,整式mx3-nx+3的值为( )
A.2022 B.2019
C.-2016 D.-2019
9.若多项式25x2-4x-6与3x3+75bx2-5x+7相加后,不含二次项,则常数k的值为( )
C.3 D.-3
10.观察下列图形,猜想第11个图形中三角形的个数为( )
…
第10题图
A.40个 B.41个
C.43个 D.45个
二、填空题(共5小题,每小题3分,计15分)
1.列式表示:比a的4倍小5的数与比b的大3的数的和,并化简:______.
12.若2x3-3x2y|m|+(m-3)x是关于x,y的五次三项式,则m的值为_____.
3.在如图的运算程序中,若开始输入的x值为3,则输出的值为_____.
14.如图,将三个大小完全相同的长方形纸片,放入一个长为 p,宽为 q 的大长方形纸盒之内,未被覆盖的部分为图中阴影部分,那么阴影部分的周长为________________.
15.用“&”定义一种新运算:a&b=3a-4b,例如:4&6=3×4-4× 6=-12;(-2)&(-5)=3×(-2)-4×(-5)=14,则当a=-2,b=3时,式子(a+2ab+3b)&(3a-ab+2b)]-3ab的值为______________________.
三、解答题(共8小题,计55分.解答应写出过程)
16.(6分)化简下列各式:
(1)-2(2x-3y2)-3(y2+2x-2);
(2)3x2-[x2+2(x2-3x-1)].
17.(6分)先化简,再求值:
(1)(-15x+3xy)(2xy-8x)-xy,其中x=2,y=-1;
(2)2(3a2a+2b-ab)-3(2a2),其中, ab=-2.
18.(6分)有理数a,b,c在数轴上的位置如图所示,化简:|-1-a|-|b-c|-|c-a|+|c-1|.
19.(7分)李老师在课堂上出了这样一道题:
小华抄题时由于粗心大意,把“”写成了“”,但他求出来的结果却是正确的,你知道为什么吗?
20.(7分)小明准备了A,B,C三张写有代数式的卡片,并且告诉同桌小华规则为:其中两张卡片上多项式的差等于第三张卡片上的多项式,但C卡片上的一部分看不清楚了.
(1)小华经过思考,对小明说:“一定不是A-B=C”,请你判断小华的说法是否正确?
(2)小明回忆起最终的结果为“C-A=B”,请你帮助小明将C卡片上的多项式补充完整.
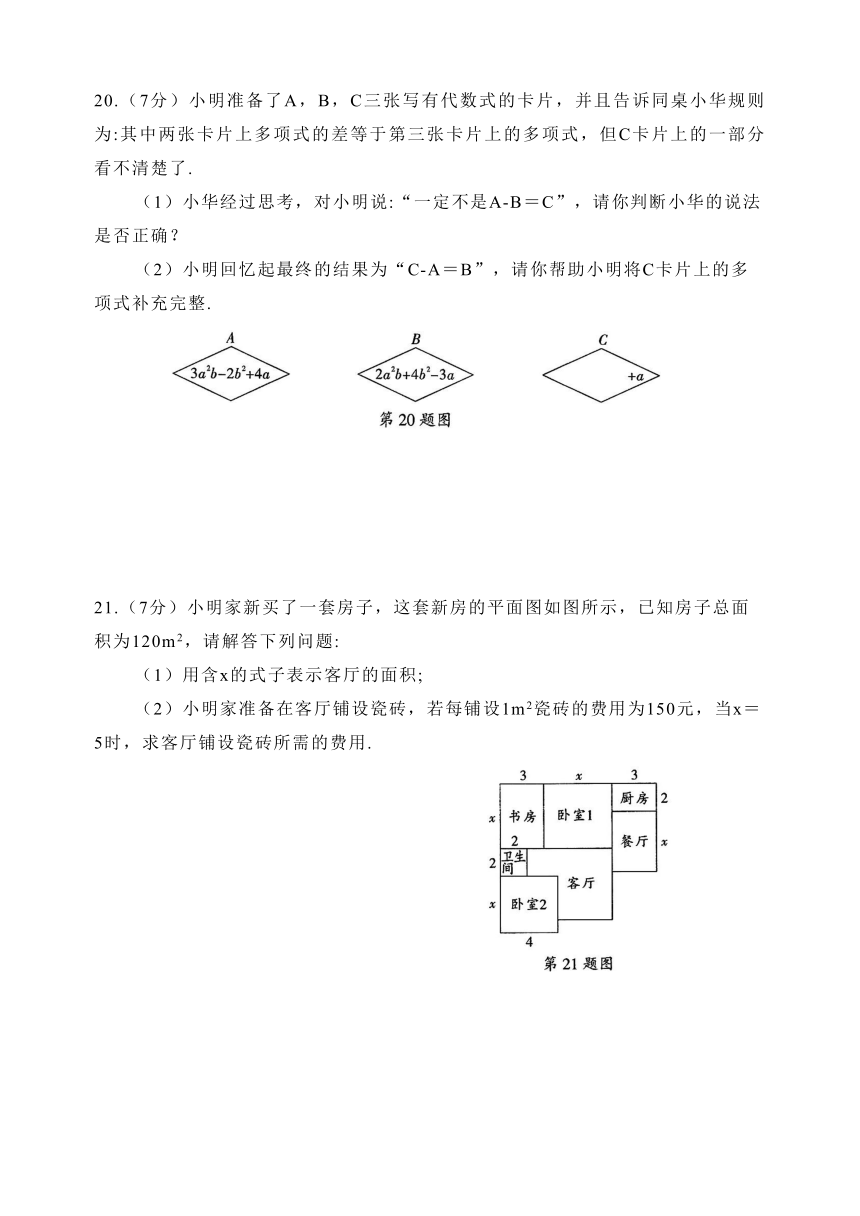
21.(7分)小明家新买了一套房子,这套新房的平面图如图所示,已知房子总面积为120m2,请解答下列问题:
(1)用含x的式子表示客厅的面积;
(2)小明家准备在客厅铺设瓷砖,若每铺设1m2瓷砖的费用为150元,当x=5时,求客厅铺设瓷砖所需的费用.
22.(7分)2022年北京冬奥会在国家体育场鸟巢举行开幕式,吉祥物“冰墩墩”成为2022开年“顶流”.某商家销售的一款“冰墩墩“毛绒玩具,每个定价200元,钥匙扣每个定价50元,并推出两种优惠方案:
方案一:购买2个毛绒玩具,赠送1个钥匙扣;
方案二:购买毛绒玩具和钥匙扣一律按9折优惠.
某公司要购买毛绒玩具和钥匙扣作为员工礼物,想要购买毛绒玩具20个,钥匙扣x个(不少于10个).
(1)若该公司采购员按方案一购买,需付款_____________________元(用含x的式子表示);若该公司采购员按方案二购买,需付款_______________________元(用含x的式子表示);
(2)当购买钥匙扣25个时,通过计算说明按照哪种方案购买较合算?
(3)当购买钥匙扣25个时,请给出一种更省钱的购买方案,并计算需要的钱数.
23.(9分)(2022版课标精神·综合与实践)数学课外活动小组的同学们利用课外活动时间举行用火柴棒拼图的实践活动.他们按照如图所示的方法拼图,探究不同图形中共拼出的三角形个数,正方形的个数及所用火柴棒的根数与所拼图序号之间的关系,请你参与进去进行数学探究活动.
(1)观察发现:观察图中正方形的个数及所用火柴棒根数,并填写下表中的空格:
(2)拓展探究:按如图所示的方法拼成的第n个图中,三角形和正方形的个数各是多少?所用的火柴棒总根数是多少?(用含n的代数式表示)
(3)当一位同学有84根火柴棒时,他拼成的图形有多少个三角形?有多少个正方形?
(4)迁移应用:按这种拼图方法拼出的第150个图中,三角形和正方形各有多少个?共需要火柴棒多少根?
答案与解析
1.C[解析]因为单项式是数或字母的积,几个单项式的和叫做多项式,所以② ⑤ 是单项式,① ③ ⑥ 是多项式,整式包含单项式与多项式,则① ② ③ ⑤ ⑥ 是整式,所以整式共有5个.
2. A
3.D[解析]的系数是,A说法正确,不符合题意;数字是单项式,B说法正确,不符合题意;根据同类项的定义,-2m2n3与3n3m2所含字母相同,并且相同字母的指数也相同,所以-2m2n3与3n3m2是同类项,C说法正确,不符合题意;32x3y的次数是4,D说法错误,符合题意.
4.B[解析]A.3a-(2a-b)=3a-2a+b,故此选项不合题意; B.2a+2(-2a-3b)=2a-4a-6b,故此选项符合题意; C.-3(a+6)=-3a-18,故此选项不合题意; D.1-(a2+b2-1)=2-a2-b2,故此选项不合题意.
5.B[解析]-(3x3ym-1)+3(xny+1)=-3x3ym+ 1+3xny+3=-3x3ym+3xny+4,因为经过化简后的结果等于4,所以-3x3ym+3xny=0,所以m=1,n= 3,所以m-n=1-3=-2.
6.C[解析]因为M=2x2-6x+11,N=3x2-6x+12,所以M-N=(2x2-6x+11)-(3x2-6x+12)=2x2-6x+11-3x2+6x-12=-x2-1=-(x2+1)<0,所以M<N.
7.C[解析]根据题意可知,这位乘客携带的行李超过20kg,且超出的部分为20kg,此部分需要购买行李票,行李票的费用为20×1.25%×b= 0.25b(元),加上他的机票钱,他乘坐该航班从长沙飞往成都的总费用为1.25b元.
8.C[解析]当x=2时,整式mx3-nx+3=2022,即8m-2n+3=2022,即8m-2n=2019,当x=-2时, mx3-nx+3=-8m+2n+3=-(8m-2n)+3= -2019+3=-2016.
9.A[解析]25x2-4x-6+3x3+75kx2-5x+7= 3x3+(25+75k)x2-9x+1,因为该式不含二次项,所以25+75k=0,解得
10.B[解析]根据题中图形可得,第1个图形中共有1个三角形,第2个图形中共有5个三角形,第3个图形中共有9个三角形,发现每个图形都比前一个图形多4个三角形,所以第n个图形中共有1+4×(n-1)=(4n-3)个三角形,那么第11个图形中共有4×11-3=41个三角形.
解析]用代数式表示比a的4倍小5的数为4a-5,用代数式表示比b的大3
的数为,两数的和为4a-5+(),去括号化简为
12.-3[解析]因为2x3-3x2y(1m+1)+(m-3)x是关于x,y的五次三项式,所以2+|m|=5,m-3≠0,所以m=-3.
13.77[解析]当x=3时,4×3-6=6,因为6<10,所以将x=6代入5+2x2中,得5+2×62=77,因为77>10,所以输出的值为77.
14.2(p+q)[解析]设小长方形的长为a,宽为b,那么阴影部分的周长为4a+6b,由题图知a+ 2b=p,a+b=q,则4a+6b=2(p+q),故阴影部分的周长为2(p+q).
15.-9[解析]原式=3(a+2ab+3b)(3a- ab+2b)]-3ab=3a+6ab+9b﹣2(3a-ab+ 2b)-3ab=3a+6ab+9b-6a+2ab-4b-3ab= -3a+5ab+5b,当a=-2,b=3时,原式=-3× (-2)+5×(-2)×3+5×3=-9.
16.解:(1)原式=-4x+6y2-3y2-6x+6
=-10x+3y2+6;
(2)原式=3x2-(x2+2x2-6x-2)
=3x2-3x2+6x+2
=6x+2.
17.解:(1)原式
,
当x=2,y=-1时,
原式(-1)=21;
(2)原式=6a2-a+4b-2ab-6a2+9a+4b-3ab
=8a+8b-5ab,
当,ab=-2时,原式=8(a+b)-5ab
(-2)
=6+10
=16.
18.解:由数轴可得b<a<-1<0<c<1,
所以-1-a>0,b-c<0,c-a>0,c-1<0,
所以原式=-1-a+(b-c)-(c-a)-(c-1)
=-1-a+b-c-c+a-c+1
=b-3c.
19.解:原式=2x3-3x2y-2xy2-x3+2xy2-y3-x3+3x2y-y3
=-2y3,
因为结果中不含x,
所以与x的取值无关.
所以小华把“”错写成“”,计算结果仍正确.
20.解:(1)A-B=3a2b-2b2+4a-(2a2b+4b2-3a)
=3a2b-2b2+4a-2a2b-4b2+3a =a2b-6b2+7a.
因为 C 卡片上的多项式中 a 的系数为1,多项式A-B中a的系数为7,
所以一定不是A-B=C,即小华的说法正确;
(2)因为C-A=B,
所以C=A+B
=3a2b-2b2+4a+2a2b+4b2-3a
=5a2b+2b2+a.
所以C卡片上的多项式为5a2b+2b2+a.
21.解:(1)客厅的面积=总面积-其余部分的面积,即
120-3x-x2-3(x+2)-4-4x
=120-3x-x2-3x-6-4-4x
=110-10x-x2;
(2)当x=5时,原式=110-10×5-52=35.
因为每铺设1m2瓷砖的费用为150元,
所以客厅铺设瓷砖所需的费用为35×150= 5250(元)
解:(1)(50x+3500);(45x+3600); [解法提示]方案一:200×20+50()=50x+ 3500,方案二:200×0.9×20+50×0.9x=45x+3600.
(2)当x=25时,方案一需付款50×25+3500= 4750(元),
方案二需付款45×25+3600=4725(元),因为4750>4725,
所以按照方案二购买比较合算;
(3)20个毛绒玩具和10个钥匙扣按照方案一购买,剩余15个钥匙扣按照方案二购买。此时需要20×200+(25-10)×50×0.9=4675(元).
23.解:(1)填空如下:
(2)第n个图中,三角形有n个,正方形有(2n+1)个,所用的火柴棒有(8n+4)根;
(3)当有84根火柴棒时,8n+4=84,所以n=10,2n+1=21,所以有10个三角形,21个正方形;
(4)第150个图形中三角形有150个,正方形有2×150+1=301(个),共需要火柴棒8×150+4=1204(根).
能力提升检测卷
时间:90分钟满分:100分
一、选择题(共10小题,每小题3分,计30分.每小题只有一个选项是符合题意的)
1.下列各式:① a-b2,② y2,③ π-,④ ,⑤ 0,⑥ -x2+y-2z3.其中整式有()
A.3个 B.4个 C.5个 D.6个
2.某种型号的电脑的标价为m元,为促进销售,商场推出促销活动.若小明的爸爸购买这款电脑的付款金额为(90%m-200)元,则下列说法中,能正确表示促销活动的是( )
A.先在标价基础上打九折,再减200元
B.先在标价基础上减200元,再整体打九折
C.先在标价基础上打一折,再减200元
D.先在标价基础上减200元,再整体打一折
3.下列说法错误的是( )
的系数是 B.数字是单项式
C. -2m2n3与3n3m2是同类项 D.32x3y的次数是5
4.下列式子中,去括号正确的是( )
A.3a-(2a-b)=3a-2a-b
B.2a+2(-2a-3b)=2a-4a-6b
C.-3(a+6)=-3a-6
D.1-(a2+b2-1)=-a2-b2
5.若整式-(3x3ym-1)+3(xny+1)经过化简后的结果等于4,则m-n的值为( )
A.2 B.-2 C.4 D.-4
6.若M=2x2-6x+11,N=3x2-6x+12,则M和N的大小关系是( )
A. M>N B.M=N
C. M<N D无法确定
7.某航空公司规定,每位乘客登机时免费携带的行李质量不能超过20kg.若超过20kg,则超出的部分,每千克要按照飞机票原价的1.25%购买行李票.已知某航班从长沙飞往成都的机票价格为b元,如果一位旅客携带了40kg的行李,那么他乘坐该航班从长沙飞往成都的总费用为( )
A.1.35b元 B.1.15b元
C.1.25b元 D.b元
8.当x=2时,整式mx3-nx+3=2022,则当x=-2时,整式mx3-nx+3的值为( )
A.2022 B.2019
C.-2016 D.-2019
9.若多项式25x2-4x-6与3x3+75bx2-5x+7相加后,不含二次项,则常数k的值为( )
C.3 D.-3
10.观察下列图形,猜想第11个图形中三角形的个数为( )
…
第10题图
A.40个 B.41个
C.43个 D.45个
二、填空题(共5小题,每小题3分,计15分)
1.列式表示:比a的4倍小5的数与比b的大3的数的和,并化简:______.
12.若2x3-3x2y|m|+(m-3)x是关于x,y的五次三项式,则m的值为_____.
3.在如图的运算程序中,若开始输入的x值为3,则输出的值为_____.
14.如图,将三个大小完全相同的长方形纸片,放入一个长为 p,宽为 q 的大长方形纸盒之内,未被覆盖的部分为图中阴影部分,那么阴影部分的周长为________________.
15.用“&”定义一种新运算:a&b=3a-4b,例如:4&6=3×4-4× 6=-12;(-2)&(-5)=3×(-2)-4×(-5)=14,则当a=-2,b=3时,式子(a+2ab+3b)&(3a-ab+2b)]-3ab的值为______________________.
三、解答题(共8小题,计55分.解答应写出过程)
16.(6分)化简下列各式:
(1)-2(2x-3y2)-3(y2+2x-2);
(2)3x2-[x2+2(x2-3x-1)].
17.(6分)先化简,再求值:
(1)(-15x+3xy)(2xy-8x)-xy,其中x=2,y=-1;
(2)2(3a2a+2b-ab)-3(2a2),其中, ab=-2.
18.(6分)有理数a,b,c在数轴上的位置如图所示,化简:|-1-a|-|b-c|-|c-a|+|c-1|.
19.(7分)李老师在课堂上出了这样一道题:
小华抄题时由于粗心大意,把“”写成了“”,但他求出来的结果却是正确的,你知道为什么吗?
20.(7分)小明准备了A,B,C三张写有代数式的卡片,并且告诉同桌小华规则为:其中两张卡片上多项式的差等于第三张卡片上的多项式,但C卡片上的一部分看不清楚了.
(1)小华经过思考,对小明说:“一定不是A-B=C”,请你判断小华的说法是否正确?
(2)小明回忆起最终的结果为“C-A=B”,请你帮助小明将C卡片上的多项式补充完整.
21.(7分)小明家新买了一套房子,这套新房的平面图如图所示,已知房子总面积为120m2,请解答下列问题:
(1)用含x的式子表示客厅的面积;
(2)小明家准备在客厅铺设瓷砖,若每铺设1m2瓷砖的费用为150元,当x=5时,求客厅铺设瓷砖所需的费用.
22.(7分)2022年北京冬奥会在国家体育场鸟巢举行开幕式,吉祥物“冰墩墩”成为2022开年“顶流”.某商家销售的一款“冰墩墩“毛绒玩具,每个定价200元,钥匙扣每个定价50元,并推出两种优惠方案:
方案一:购买2个毛绒玩具,赠送1个钥匙扣;
方案二:购买毛绒玩具和钥匙扣一律按9折优惠.
某公司要购买毛绒玩具和钥匙扣作为员工礼物,想要购买毛绒玩具20个,钥匙扣x个(不少于10个).
(1)若该公司采购员按方案一购买,需付款_____________________元(用含x的式子表示);若该公司采购员按方案二购买,需付款_______________________元(用含x的式子表示);
(2)当购买钥匙扣25个时,通过计算说明按照哪种方案购买较合算?
(3)当购买钥匙扣25个时,请给出一种更省钱的购买方案,并计算需要的钱数.
23.(9分)(2022版课标精神·综合与实践)数学课外活动小组的同学们利用课外活动时间举行用火柴棒拼图的实践活动.他们按照如图所示的方法拼图,探究不同图形中共拼出的三角形个数,正方形的个数及所用火柴棒的根数与所拼图序号之间的关系,请你参与进去进行数学探究活动.
(1)观察发现:观察图中正方形的个数及所用火柴棒根数,并填写下表中的空格:
(2)拓展探究:按如图所示的方法拼成的第n个图中,三角形和正方形的个数各是多少?所用的火柴棒总根数是多少?(用含n的代数式表示)
(3)当一位同学有84根火柴棒时,他拼成的图形有多少个三角形?有多少个正方形?
(4)迁移应用:按这种拼图方法拼出的第150个图中,三角形和正方形各有多少个?共需要火柴棒多少根?
答案与解析
1.C[解析]因为单项式是数或字母的积,几个单项式的和叫做多项式,所以② ⑤ 是单项式,① ③ ⑥ 是多项式,整式包含单项式与多项式,则① ② ③ ⑤ ⑥ 是整式,所以整式共有5个.
2. A
3.D[解析]的系数是,A说法正确,不符合题意;数字是单项式,B说法正确,不符合题意;根据同类项的定义,-2m2n3与3n3m2所含字母相同,并且相同字母的指数也相同,所以-2m2n3与3n3m2是同类项,C说法正确,不符合题意;32x3y的次数是4,D说法错误,符合题意.
4.B[解析]A.3a-(2a-b)=3a-2a+b,故此选项不合题意; B.2a+2(-2a-3b)=2a-4a-6b,故此选项符合题意; C.-3(a+6)=-3a-18,故此选项不合题意; D.1-(a2+b2-1)=2-a2-b2,故此选项不合题意.
5.B[解析]-(3x3ym-1)+3(xny+1)=-3x3ym+ 1+3xny+3=-3x3ym+3xny+4,因为经过化简后的结果等于4,所以-3x3ym+3xny=0,所以m=1,n= 3,所以m-n=1-3=-2.
6.C[解析]因为M=2x2-6x+11,N=3x2-6x+12,所以M-N=(2x2-6x+11)-(3x2-6x+12)=2x2-6x+11-3x2+6x-12=-x2-1=-(x2+1)<0,所以M<N.
7.C[解析]根据题意可知,这位乘客携带的行李超过20kg,且超出的部分为20kg,此部分需要购买行李票,行李票的费用为20×1.25%×b= 0.25b(元),加上他的机票钱,他乘坐该航班从长沙飞往成都的总费用为1.25b元.
8.C[解析]当x=2时,整式mx3-nx+3=2022,即8m-2n+3=2022,即8m-2n=2019,当x=-2时, mx3-nx+3=-8m+2n+3=-(8m-2n)+3= -2019+3=-2016.
9.A[解析]25x2-4x-6+3x3+75kx2-5x+7= 3x3+(25+75k)x2-9x+1,因为该式不含二次项,所以25+75k=0,解得
10.B[解析]根据题中图形可得,第1个图形中共有1个三角形,第2个图形中共有5个三角形,第3个图形中共有9个三角形,发现每个图形都比前一个图形多4个三角形,所以第n个图形中共有1+4×(n-1)=(4n-3)个三角形,那么第11个图形中共有4×11-3=41个三角形.
解析]用代数式表示比a的4倍小5的数为4a-5,用代数式表示比b的大3
的数为,两数的和为4a-5+(),去括号化简为
12.-3[解析]因为2x3-3x2y(1m+1)+(m-3)x是关于x,y的五次三项式,所以2+|m|=5,m-3≠0,所以m=-3.
13.77[解析]当x=3时,4×3-6=6,因为6<10,所以将x=6代入5+2x2中,得5+2×62=77,因为77>10,所以输出的值为77.
14.2(p+q)[解析]设小长方形的长为a,宽为b,那么阴影部分的周长为4a+6b,由题图知a+ 2b=p,a+b=q,则4a+6b=2(p+q),故阴影部分的周长为2(p+q).
15.-9[解析]原式=3(a+2ab+3b)(3a- ab+2b)]-3ab=3a+6ab+9b﹣2(3a-ab+ 2b)-3ab=3a+6ab+9b-6a+2ab-4b-3ab= -3a+5ab+5b,当a=-2,b=3时,原式=-3× (-2)+5×(-2)×3+5×3=-9.
16.解:(1)原式=-4x+6y2-3y2-6x+6
=-10x+3y2+6;
(2)原式=3x2-(x2+2x2-6x-2)
=3x2-3x2+6x+2
=6x+2.
17.解:(1)原式
,
当x=2,y=-1时,
原式(-1)=21;
(2)原式=6a2-a+4b-2ab-6a2+9a+4b-3ab
=8a+8b-5ab,
当,ab=-2时,原式=8(a+b)-5ab
(-2)
=6+10
=16.
18.解:由数轴可得b<a<-1<0<c<1,
所以-1-a>0,b-c<0,c-a>0,c-1<0,
所以原式=-1-a+(b-c)-(c-a)-(c-1)
=-1-a+b-c-c+a-c+1
=b-3c.
19.解:原式=2x3-3x2y-2xy2-x3+2xy2-y3-x3+3x2y-y3
=-2y3,
因为结果中不含x,
所以与x的取值无关.
所以小华把“”错写成“”,计算结果仍正确.
20.解:(1)A-B=3a2b-2b2+4a-(2a2b+4b2-3a)
=3a2b-2b2+4a-2a2b-4b2+3a =a2b-6b2+7a.
因为 C 卡片上的多项式中 a 的系数为1,多项式A-B中a的系数为7,
所以一定不是A-B=C,即小华的说法正确;
(2)因为C-A=B,
所以C=A+B
=3a2b-2b2+4a+2a2b+4b2-3a
=5a2b+2b2+a.
所以C卡片上的多项式为5a2b+2b2+a.
21.解:(1)客厅的面积=总面积-其余部分的面积,即
120-3x-x2-3(x+2)-4-4x
=120-3x-x2-3x-6-4-4x
=110-10x-x2;
(2)当x=5时,原式=110-10×5-52=35.
因为每铺设1m2瓷砖的费用为150元,
所以客厅铺设瓷砖所需的费用为35×150= 5250(元)
解:(1)(50x+3500);(45x+3600); [解法提示]方案一:200×20+50()=50x+ 3500,方案二:200×0.9×20+50×0.9x=45x+3600.
(2)当x=25时,方案一需付款50×25+3500= 4750(元),
方案二需付款45×25+3600=4725(元),因为4750>4725,
所以按照方案二购买比较合算;
(3)20个毛绒玩具和10个钥匙扣按照方案一购买,剩余15个钥匙扣按照方案二购买。此时需要20×200+(25-10)×50×0.9=4675(元).
23.解:(1)填空如下:
(2)第n个图中,三角形有n个,正方形有(2n+1)个,所用的火柴棒有(8n+4)根;
(3)当有84根火柴棒时,8n+4=84,所以n=10,2n+1=21,所以有10个三角形,21个正方形;
(4)第150个图形中三角形有150个,正方形有2×150+1=301(个),共需要火柴棒8×150+4=1204(根).
