平方差公式课件

课件23张PPT。计算下列多项式的积： (x+1)(x-1) =
(m+2)(m-2) =
(2x+1)(2x-1) =x2 - 1m2 - 44x2 - 1观察算式及结果，你发现有什么规律？
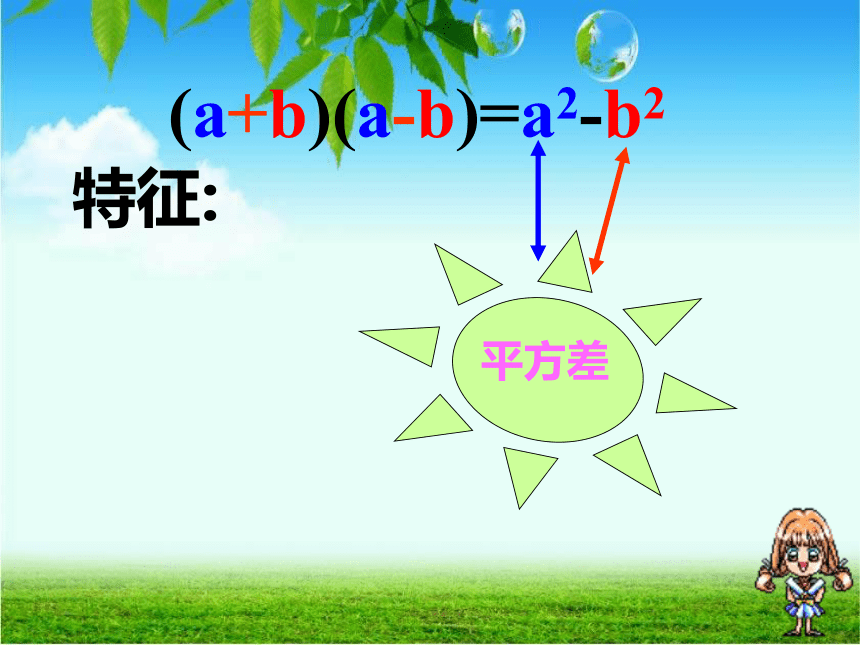
第六章 整式乘除(a+b)(a-b)=a2-b2
两个数的和 与这两个数的差的积，
等于这两个数的平方差。 (a+b)(a-b)=a2-b2
特征:(a+b)(a-b)=a2-b2
特征:(a+b)(a-b)=a2-b2
特征:(a+b)(a-b)=a2-b2
特征:(a+b)(a-b)=a2-b2
特征:(a+b)(a-b)=a2-b2
特征:(a+b)(a-b)=a2-b2
说明: 公式中的a,b可以表示
一个单项式也可以表示一个多项式.选择下列各式中,能用平方差公式运算的是( )
A.(a+b)(-a-b) B.(a-b)(b+a)
C.(2a-3b)(3a+2b) D.(a-b+c)(b-a-c)
2.下列多项式相乘,不能用平方差公式计算的是( )
A.(x-2y)(2y+x) B.(-x+2y)(-x-2y)
C.(-2y-x)(x+2y) D.(-2b-5)(2b-5)BC例1 运用平方差公式计算： ⑴ (3x+2)(3x-2) ;⑵ (b+2a)(2a-b); (3) (-x+2y)(-x-2y).分析: ⑴ (3x+2)(3x-2) 3x3xaa22bb= a2 - b2=(3x)2-22用公式关键是识别两数
完全相同项 — a
互为相反数项— b解: ⑴ (3x+2)(3x-2) =(3x)23x3x-2222= 9x2 - 4⑵ (b+2a)(2a-b);b-b+2a2a=(2a+b)(2a-b)2a2a=(2a)2 =4a2 – b2bb-b2 积的乘方要加括号 (3) (-x+2y)(-x-2y) = (-x)2-(2y)2= x2-4y2
自学例2
同桌交流并总结注意事项
完成课本习题第一题符号相同项，要连同符号添加括号。所有字母添加括号。大胆试一试：运用平方差公式计算：
1.(an+b)(an-b)
2. . (x+2) (x-2) (x2+4) 平方差公式重复运用： 计算二次应用一次应用
1、平方差公式是特殊的多项式乘法，要理解并掌握公式的结构特征.
??? 2、计算中注意公式的重复使用，确保结果最简。 2) 右边是相同项的平方减互为相反数的 项的平方.1) 左边是两个二项式相乘，其中一 项完全相同，另一项互为相反数.谈谈你的学习心得应用时注意：
1）要先确定平方差公式中的“a”和“b”.
2）把系数和所有字母一起用括号括起来再平方
课堂达标1.(-a+b)(-a-b)=--- 2.(a+b)(b-a)=----
3.(-a+b)(a+b) =--- 4.(a-b)(b+a) =- -- a2-b2 b2-a2b2-a2a2-b2 二.下列计算对不对？如果不对，说出理由并改正？
2)错1) 分析：最后结果应是两项的平方差错 3) 分析：应是相同项的平方减互为相反数的项的平方 错 4) 分析：不满足平方差公式的特点，没有相同项 错 分析：应将 当作一个整体，用括号括起来再平方 三.运用平方差公式计算：1、(m+n)(-n+m) =
2、(-x-y) (x-y) =
3、(2a+b)(2a-b) =
4、(x2+y2)(x2-y2)=
5. (x+1) (x-1) (x2+1) =
m2-n2y2-x24a2-b2x4-y4(a+b)(a-b)=a2-b2
x4-1www.czsx.com.cn