11.3 多边形及其内角和同步练习(含答案)
文档属性
| 名称 | 11.3 多边形及其内角和同步练习(含答案) | 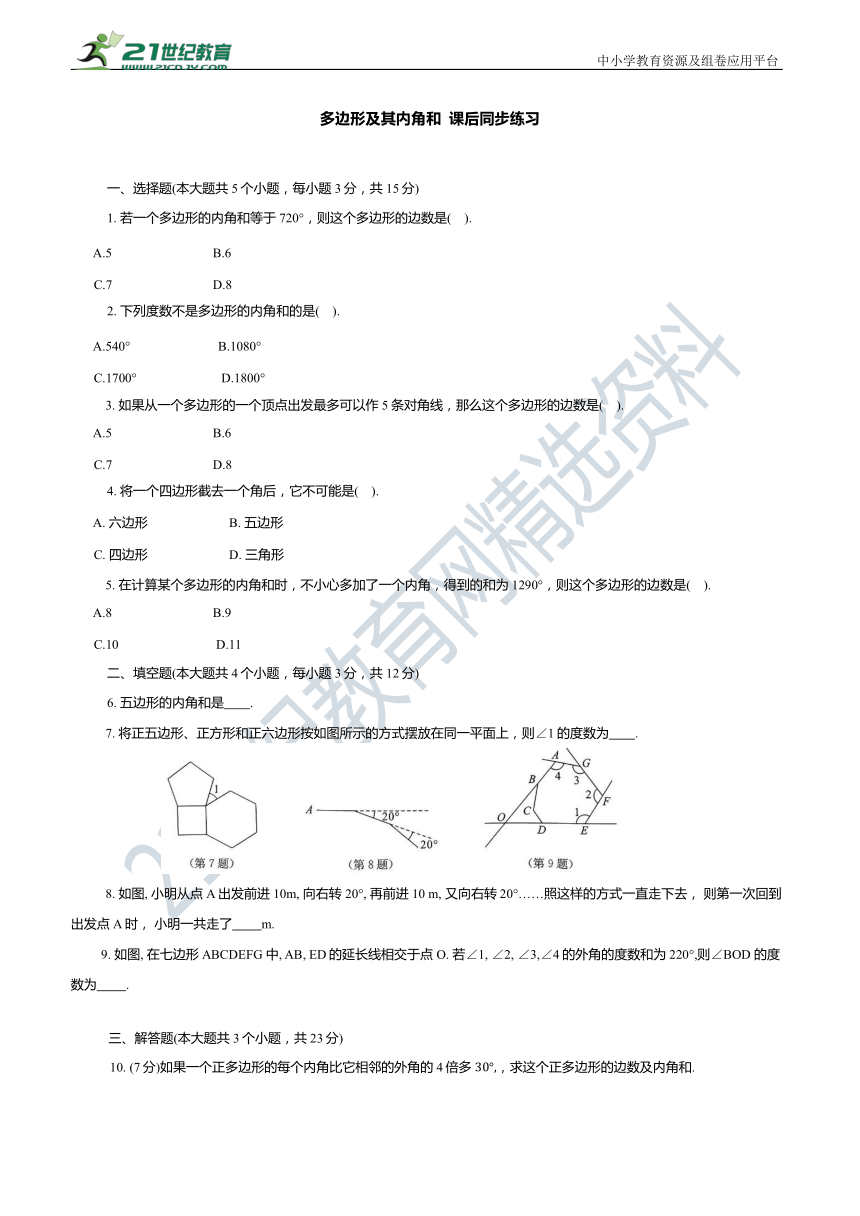 | |
| 格式 | docx | ||
| 文件大小 | 482.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-25 10:47:26 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
多边形及其内角和 课后同步练习
一、选择题(本大题共5个小题,每小题3分,共15分)
1. 若一个多边形的内角和等于720°,则这个多边形的边数是( ).
A.5 B.6
C.7 D.8
2. 下列度数不是多边形的内角和的是( ).
A.540° B.1080°
C.1700° D.1800°
3. 如果从一个多边形的一个顶点出发最多可以作5条对角线,那么这个多边形的边数是( ).
A.5 B.6
C.7 D.8
4. 将一个四边形截去一个角后,它不可能是( ).
A. 六边形 B. 五边形
C. 四边形 D. 三角形
5. 在计算某个多边形的内角和时,不小心多加了一个内角,得到的和为1290°,则这个多边形的边数是( ).
A.8 B.9
C.10 D.11
二、填空题(本大题共4个小题,每小题3分,共12分)
6. 五边形的内角和是 .
7. 将正五边形、正方形和正六边形按如图所示的方式摆放在同一平面上,则∠1的度数为 .
8. 如图, 小明从点A 出发前进10m, 向右转20°, 再前进10 m, 又向右转20°……照这样的方式一直走下去, 则第一次回到出发点A时, 小明一共走了 m.
9. 如图, 在七边形ABCDEFG 中, AB, ED的延长线相交于点O. 若∠1, ∠2, ∠3,∠4的外角的度数和为220°,则∠BOD 的度数为 .
三、解答题(本大题共3个小题,共23分)
10. (7分)如果一个正多边形的每个内角比它相邻的外角的4倍多 ,求这个正多边形的边数及内角和.
11. (8分)如图,P 是四边形 ABCD 的外角∠CDE 和外角. 的平分线的交点.若∠A=149°, ∠B=91°, 求∠P 的度数.
12. (8分)如图①所示的图形称为“对顶三角形”,其中 . 请利用这个结论解答下列各题.
(1)如图②,求 的和;
(2)如图③,求 的和;
(3)如图④,求. 的和,并说明理由;
(4)如图⑤,求 的和,并说明理由.
1. B 2. C 3. D 4. A 5. B
6.540° 7.42° 8.180 9.40°
10. 设这个正多边形的一个外角为x°,则与它相邻的内角为(4x+30)°.
由题意得x+4x+30=180,解得 x=30,
故这个多边形的边数为. 内角和为(
11.∵四边形的内角和为360°, ∴∠BCD+∠ADC=360°-∠A-∠B=120°,
∴∠CDE+∠DCF=240°.
∵P 是四边形ABCD 的外角∠CDE 和外角∠DCF 的平分线的交点,
12. (1)180° (2)180°
(3)360°. 理由如下: 如图①,连接AB.
∵∠1+∠2=∠7+∠8,
∴∠1+∠2+∠3+∠4+∠5+∠6
=∠3+∠4+∠5+∠6+∠7+∠8
=360°.
(4)540°. 理由如下: 如图②, 连接AB.
∵∠6+∠7=∠8+∠9,
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7
=∠1+∠2+∠3+∠4+∠5+∠8+∠9
多边形及其内角和 课后同步练习
一、选择题(本大题共5个小题,每小题3分,共15分)
1. 若一个多边形的内角和等于720°,则这个多边形的边数是( ).
A.5 B.6
C.7 D.8
2. 下列度数不是多边形的内角和的是( ).
A.540° B.1080°
C.1700° D.1800°
3. 如果从一个多边形的一个顶点出发最多可以作5条对角线,那么这个多边形的边数是( ).
A.5 B.6
C.7 D.8
4. 将一个四边形截去一个角后,它不可能是( ).
A. 六边形 B. 五边形
C. 四边形 D. 三角形
5. 在计算某个多边形的内角和时,不小心多加了一个内角,得到的和为1290°,则这个多边形的边数是( ).
A.8 B.9
C.10 D.11
二、填空题(本大题共4个小题,每小题3分,共12分)
6. 五边形的内角和是 .
7. 将正五边形、正方形和正六边形按如图所示的方式摆放在同一平面上,则∠1的度数为 .
8. 如图, 小明从点A 出发前进10m, 向右转20°, 再前进10 m, 又向右转20°……照这样的方式一直走下去, 则第一次回到出发点A时, 小明一共走了 m.
9. 如图, 在七边形ABCDEFG 中, AB, ED的延长线相交于点O. 若∠1, ∠2, ∠3,∠4的外角的度数和为220°,则∠BOD 的度数为 .
三、解答题(本大题共3个小题,共23分)
10. (7分)如果一个正多边形的每个内角比它相邻的外角的4倍多 ,求这个正多边形的边数及内角和.
11. (8分)如图,P 是四边形 ABCD 的外角∠CDE 和外角. 的平分线的交点.若∠A=149°, ∠B=91°, 求∠P 的度数.
12. (8分)如图①所示的图形称为“对顶三角形”,其中 . 请利用这个结论解答下列各题.
(1)如图②,求 的和;
(2)如图③,求 的和;
(3)如图④,求. 的和,并说明理由;
(4)如图⑤,求 的和,并说明理由.
1. B 2. C 3. D 4. A 5. B
6.540° 7.42° 8.180 9.40°
10. 设这个正多边形的一个外角为x°,则与它相邻的内角为(4x+30)°.
由题意得x+4x+30=180,解得 x=30,
故这个多边形的边数为. 内角和为(
11.∵四边形的内角和为360°, ∴∠BCD+∠ADC=360°-∠A-∠B=120°,
∴∠CDE+∠DCF=240°.
∵P 是四边形ABCD 的外角∠CDE 和外角∠DCF 的平分线的交点,
12. (1)180° (2)180°
(3)360°. 理由如下: 如图①,连接AB.
∵∠1+∠2=∠7+∠8,
∴∠1+∠2+∠3+∠4+∠5+∠6
=∠3+∠4+∠5+∠6+∠7+∠8
=360°.
(4)540°. 理由如下: 如图②, 连接AB.
∵∠6+∠7=∠8+∠9,
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7
=∠1+∠2+∠3+∠4+∠5+∠8+∠9
