13.3 等腰三角形的性质与判定同步练习(含答案)
文档属性
| 名称 | 13.3 等腰三角形的性质与判定同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 793.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-25 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
等腰三角形的性质与判定 课后同步练习
一、选择题(本大题共4个小题,每小题3分,共12分)
1. 如图, 在△ABC中, AB=AC, AD为∠BAC 的平分线. 若 AD=5, BC=4, 则图中阴影部分的面积是( ).
A.5 B.6 C.7 D.10
2. 如果一个等腰三角形的两条边长分别是9cm和5cm,那么这个等腰三角形的周长是( ).
A.14 cm B.19 cm C.23 cm D.19 cm或23 cm
3. 如图, 在Rt△ABC 中, ∠C=90°, ∠A =30°, 在直线 BC 上任取一点 P, 使得△PAB是等腰三角形,则符合条件的点 P 有( ).
A.2个 B.4个 C.6个 D.8个
4. 如图, 在△ABC 中, AD 平分∠BAC, AD⊥BD 于点 D. 已知S△ABC =12,则S△ADc=( ).
A.10 B.8 C.6 D.4
二、填空题(本大题共4个小题,每小题3分,共12分)
5. 如图, 在△ABC中, AB=BC, 过点A作DE∥BC. 若∠1=42°, 则∠2的度数为 .
6. 如图,在△ABC中,AB, AC 的垂直平分线分别交边BC 于点E, F. 若∠BAC=126°, 则∠EAF 的度数是 .
7. 如图, 在△ABC中, 点 D 在边BC上, E 为CD 的中点, 且BD=AD=AC. 若∠CAE=18°, 则∠B 的度数为 .
8. 如图, D 为△ABC 的边 BC 上一点, AB =CB, AC =AD, ∠BAD =24°, 则∠C的度数为 .
三、解答题(本大题共 3个小题,共 26分)
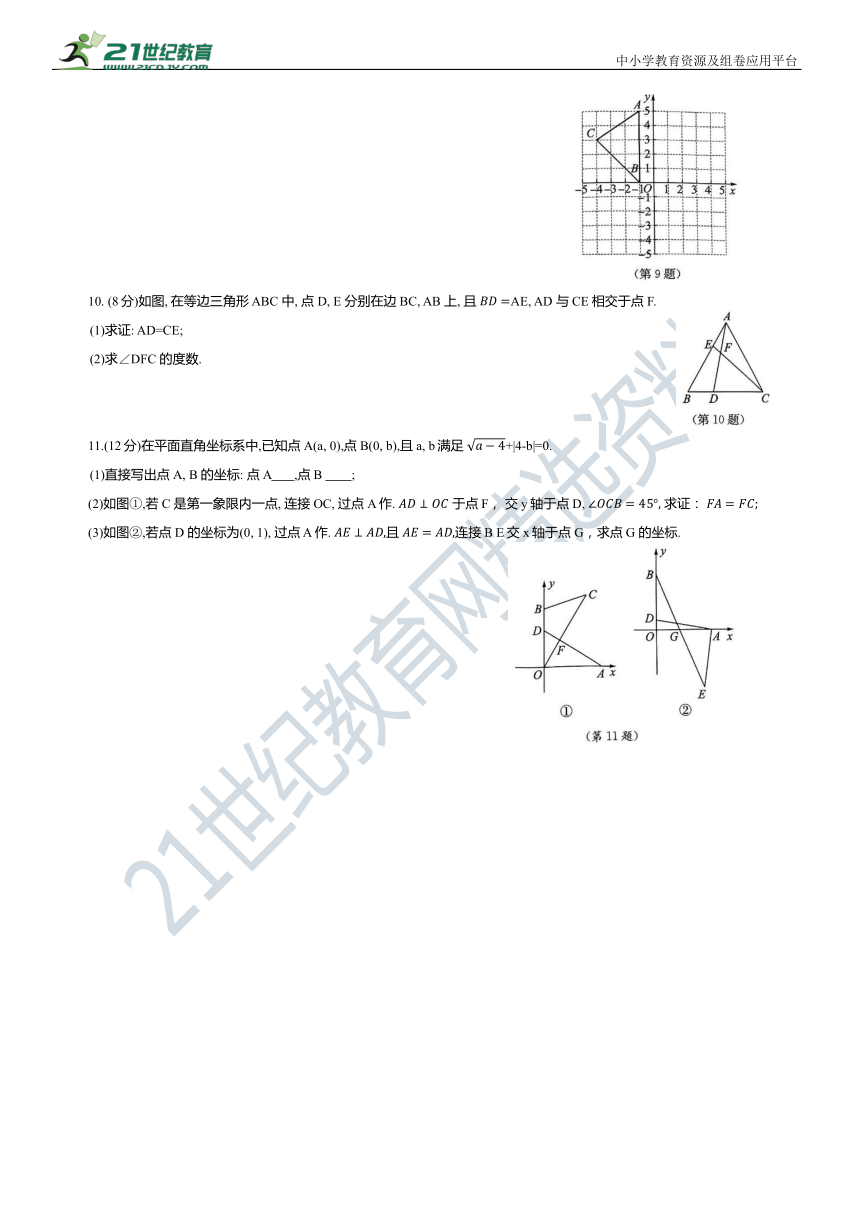
9. (6分)如图, 在平面直角坐标系中, 已知 的顶点坐标分别为 B(-1, 0), C(-4, 3).
(1)求△ABC 的面积;
(2)在平面直角坐标系中作出 关于y轴的对称图形 (点A, B, C 的对应点分别为 并写出点. 的坐标;
(3)是否存在一点 P 到AC,AB 的距离相等,并且到点A,B 的距离也相等 若存在,标出点 P 的位置(保留作图痕迹);若不存在,请说明理由.
10. (8分)如图, 在等边三角形 ABC 中, 点 D, E 分别在边BC, AB 上, 且 AE, AD 与CE 相交于点F.
(1)求证: AD=CE;
(2)求∠DFC 的度数.
11.(12分)在平面直角坐标系中,已知点A(a, 0),点B(0, b),且a, b满足 +|4-b|=0.
(1)直接写出点A, B 的坐标: 点A ,点B ;
(2)如图①,若C 是第一象限内一点, 连接OC, 过点A 作. 于点F, 交y轴于点 D, 求证:
(3)如图②,若点 D 的坐标为(0, 1), 过点 A 作. 且 连接B E交x轴于点G,求点G 的坐标.
1. A 2. D 3. A 4. C
5.69° 6.72° 7.36° 8.68°
(2)如图,△A B C 即为所求,
(3)如图,点 P 即为所求, 点 P 为∠CAB 的平分线与线段AB 的垂直平分线的交点.
10. (1)∵△ABC是等边三角形, ∴∠BAC=∠B=60°, AB=AC.
又∵AE=BD, ∴△AEC≌△BDA. ∴AD=CE.
(2)由(1)知△AEC≌△BDA, ∴∠ACE=∠BAD,
∴∠DFC=∠FAC+∠ACE=∠FAC+∠BAD=∠BAC=60°.
11. (1)由题意得a=4, b=4, ∴ 点A, B的坐标分别是A(4, 0), B(0, 4).
(2)如图①,作 BE⊥CO于点E, .
由(1)知OA=OB=4.
∵AD⊥OC,
∴∠AOF+∠OAF=90°.
∵∠BOE+∠AOE=90°,
∴∠BOE=∠OAF, ∴ △BEO≌△OFA, ∴BE=OF, OE=AF.
∵∠OCB=45°, ∴ BE=CE,
∴OF=CE, ∴OE=CF, ∴AF=CF.
(3)如图②, 作 EF⊥x轴于点F, ∴∠EFA=∠EFG=90°, ∠FEA+∠FAE=90°.
∵AE⊥AD, ∴∠DAE=90°, ∴∠DAO=∠AEF.
∴△AOD≌△EFA, ∴ AO=EF, OD=FA, ∴BO=EF.
又∵∠BOG=∠EFG, ∠BGO=∠EGF,
∴△BOG≌△EFG, ∴OG=FG.
∵OD=1, ∴ AF=1, ∴OF=3, ∴OG=1.5, ∴G(1.5, 0).
等腰三角形的性质与判定 课后同步练习
一、选择题(本大题共4个小题,每小题3分,共12分)
1. 如图, 在△ABC中, AB=AC, AD为∠BAC 的平分线. 若 AD=5, BC=4, 则图中阴影部分的面积是( ).
A.5 B.6 C.7 D.10
2. 如果一个等腰三角形的两条边长分别是9cm和5cm,那么这个等腰三角形的周长是( ).
A.14 cm B.19 cm C.23 cm D.19 cm或23 cm
3. 如图, 在Rt△ABC 中, ∠C=90°, ∠A =30°, 在直线 BC 上任取一点 P, 使得△PAB是等腰三角形,则符合条件的点 P 有( ).
A.2个 B.4个 C.6个 D.8个
4. 如图, 在△ABC 中, AD 平分∠BAC, AD⊥BD 于点 D. 已知S△ABC =12,则S△ADc=( ).
A.10 B.8 C.6 D.4
二、填空题(本大题共4个小题,每小题3分,共12分)
5. 如图, 在△ABC中, AB=BC, 过点A作DE∥BC. 若∠1=42°, 则∠2的度数为 .
6. 如图,在△ABC中,AB, AC 的垂直平分线分别交边BC 于点E, F. 若∠BAC=126°, 则∠EAF 的度数是 .
7. 如图, 在△ABC中, 点 D 在边BC上, E 为CD 的中点, 且BD=AD=AC. 若∠CAE=18°, 则∠B 的度数为 .
8. 如图, D 为△ABC 的边 BC 上一点, AB =CB, AC =AD, ∠BAD =24°, 则∠C的度数为 .
三、解答题(本大题共 3个小题,共 26分)
9. (6分)如图, 在平面直角坐标系中, 已知 的顶点坐标分别为 B(-1, 0), C(-4, 3).
(1)求△ABC 的面积;
(2)在平面直角坐标系中作出 关于y轴的对称图形 (点A, B, C 的对应点分别为 并写出点. 的坐标;
(3)是否存在一点 P 到AC,AB 的距离相等,并且到点A,B 的距离也相等 若存在,标出点 P 的位置(保留作图痕迹);若不存在,请说明理由.
10. (8分)如图, 在等边三角形 ABC 中, 点 D, E 分别在边BC, AB 上, 且 AE, AD 与CE 相交于点F.
(1)求证: AD=CE;
(2)求∠DFC 的度数.
11.(12分)在平面直角坐标系中,已知点A(a, 0),点B(0, b),且a, b满足 +|4-b|=0.
(1)直接写出点A, B 的坐标: 点A ,点B ;
(2)如图①,若C 是第一象限内一点, 连接OC, 过点A 作. 于点F, 交y轴于点 D, 求证:
(3)如图②,若点 D 的坐标为(0, 1), 过点 A 作. 且 连接B E交x轴于点G,求点G 的坐标.
1. A 2. D 3. A 4. C
5.69° 6.72° 7.36° 8.68°
(2)如图,△A B C 即为所求,
(3)如图,点 P 即为所求, 点 P 为∠CAB 的平分线与线段AB 的垂直平分线的交点.
10. (1)∵△ABC是等边三角形, ∴∠BAC=∠B=60°, AB=AC.
又∵AE=BD, ∴△AEC≌△BDA. ∴AD=CE.
(2)由(1)知△AEC≌△BDA, ∴∠ACE=∠BAD,
∴∠DFC=∠FAC+∠ACE=∠FAC+∠BAD=∠BAC=60°.
11. (1)由题意得a=4, b=4, ∴ 点A, B的坐标分别是A(4, 0), B(0, 4).
(2)如图①,作 BE⊥CO于点E, .
由(1)知OA=OB=4.
∵AD⊥OC,
∴∠AOF+∠OAF=90°.
∵∠BOE+∠AOE=90°,
∴∠BOE=∠OAF, ∴ △BEO≌△OFA, ∴BE=OF, OE=AF.
∵∠OCB=45°, ∴ BE=CE,
∴OF=CE, ∴OE=CF, ∴AF=CF.
(3)如图②, 作 EF⊥x轴于点F, ∴∠EFA=∠EFG=90°, ∠FEA+∠FAE=90°.
∵AE⊥AD, ∴∠DAE=90°, ∴∠DAO=∠AEF.
∴△AOD≌△EFA, ∴ AO=EF, OD=FA, ∴BO=EF.
又∵∠BOG=∠EFG, ∠BGO=∠EGF,
∴△BOG≌△EFG, ∴OG=FG.
∵OD=1, ∴ AF=1, ∴OF=3, ∴OG=1.5, ∴G(1.5, 0).
