8.2.1代入消元法解二元一次方程组课件
文档属性
| 名称 | 8.2.1代入消元法解二元一次方程组课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 333.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-12 08:43:57 | ||
图片预览








文档简介
课件34张PPT。 8.2.1 消元
——用代入法解二元一次方程组 “一切问题都可以转化为数学问题,一切数学问题都可以转化为代数问题,而一切代数问题又都可以转化为方程问题,因此,一旦解决了方程问题,一切问题将迎刃而解!”
——法国数学家 笛卡儿[Descartes, 1596-1650 ]名人语录
1、会用代入法解二元一次方程组。
2、体会解二元一次方程组的基本思想—“消元”。
确立目标 问题1:什么是二元一次方程?含有两个未知数,并且所含未知数的项的次数都是1的方程叫做二元一次方程。问题4:什么是二元一次方程组的解?问题2:什么是二元一次方程组?把具有相同未知数的两个二元一次方程合在一起,
就组成了一个二元一次方程组。 二元一次方程组的两个方程的公共解,叫做二元
一次方程组的解。
回顾与思考 问题3:什么是二元一次方程的解?使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解.1. 把下列方程写成用含x的式子表示y的形式.(2)课前热身 2.你能把上面两个方程写成用含y的式子表示x的形式?
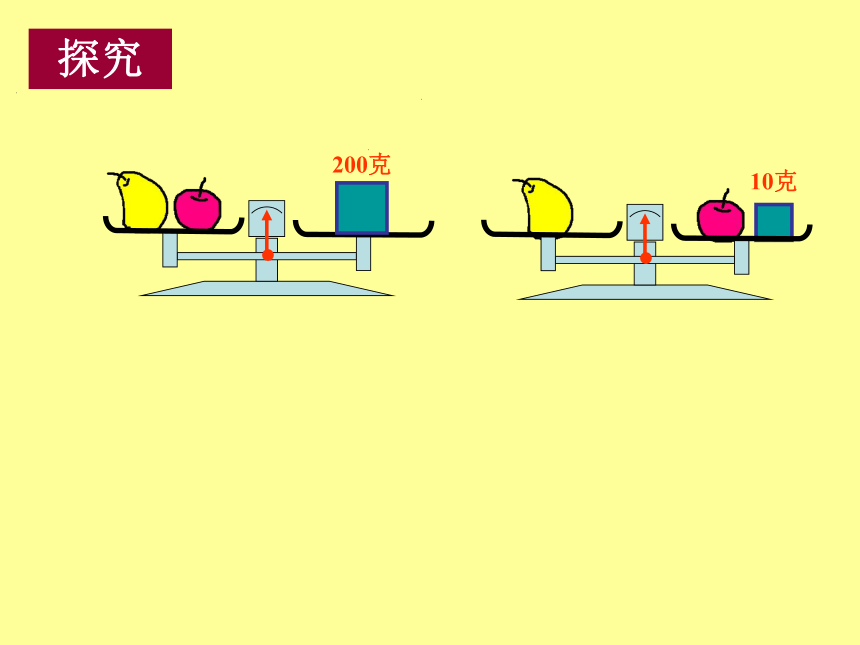
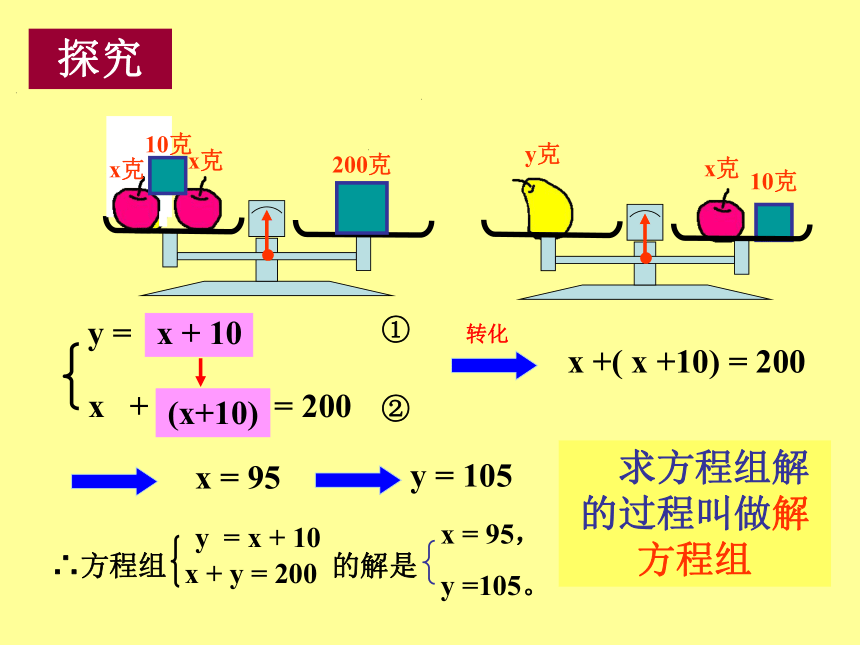
(1)(1)(2)3.如何解这样的方程组探究 x + y = 200y = x + 10x克10克(x+10)x +( x +10) = 200①②x = 95y = 105 求方程组解的过程叫做解方程组转化探究 解二元一次方程组一元一次方程二元一次方程组消 元用代入法转化将未知数的个数由多化少,逐一解决的想法,
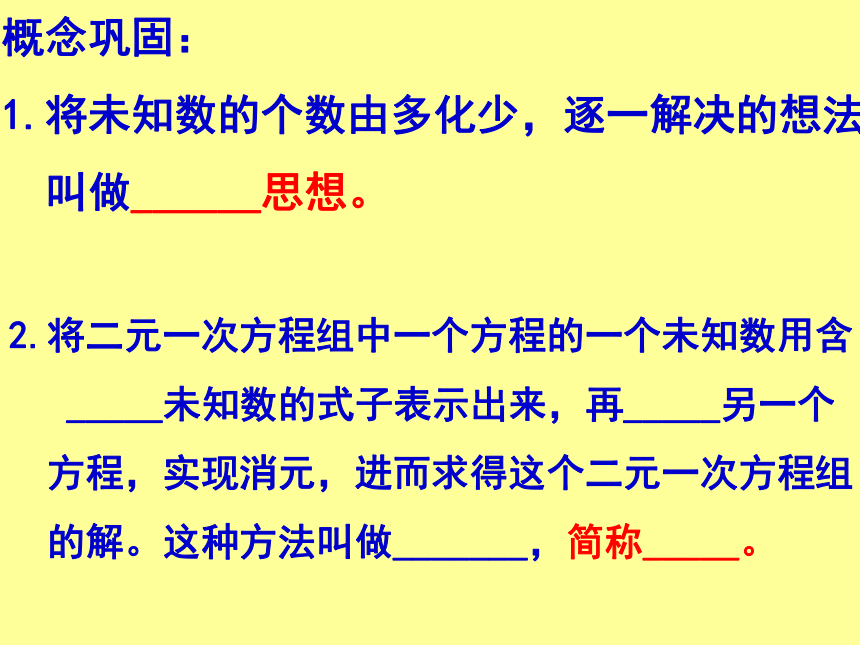
叫做消元思想。将二元一次方程组中一个方程的一个未知数用含另一未知数的式子表示出来,再代入另一个方程,实现消元,进而求得这个二元一次方程组的解。这种方法叫做代入消元法,简称代入法。概念巩固:
1.将未知数的个数由多化少,逐一解决的想法,
叫做______思想。2.将二元一次方程组中一个方程的一个未知数用含
_____未知数的式子表示出来,再_____另一个
方程,实现消元,进而求得这个二元一次方程组
的解。这种方法叫做_______,简称_____。解:①②把②代入①得:2y – 3(y – 1)= 1 y = 2把y = 2代入②,得x = y – 1 = 2 – 1 = 12 y – 3 x = 1x = y - 1(y-1)谈谈思路 例2 解方程组解:由①得:x = 3+y③把③代入②得:3(3+y)–8y= 141、将方程组里的一个方程变 形,用含有一个未知数的式子表示另一个未知数;2、用这个式子代替另一个方程中相应的未知数,得到一个一元一次方程。4、把这个未知数的值代入上面的式子,求得另一个未知数的值;5、写出方程组的解。变形代入求解写解解这个方程,得y= – 1把y= – 1代入③,得x = 3+(-1)=2回代3.解这个一元一次方程,
求得一个未知数的值;
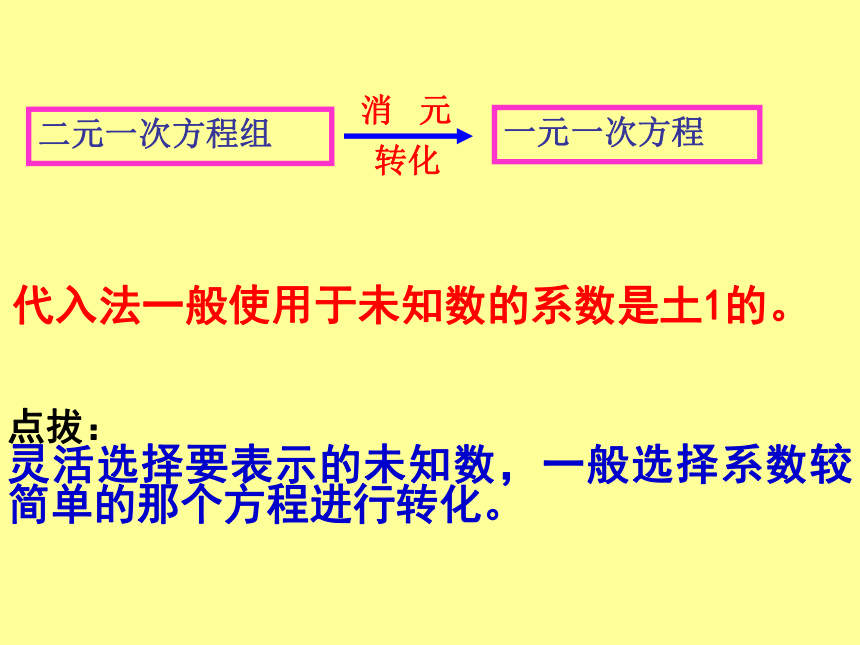
一元一次方程二元一次方程组消 元转化代入法一般使用于未知数的系数是土1的。点拔:
灵活选择要表示的未知数,一般选择系数较简单的那个方程进行转化。
1.把下列方程写成用含x的式子表示y的形式。
①2x-y=3 ②3x+y-1=0 ③3x+2y=10
2.用代入法解二元一次方程组.
(1) (2) (3)练一练
(4)2a=1-b (5) + =
5a+3b=4 2(x-5)+(y+5)=-23.用代入法解二元一次方程组 3x+4y=2 ①时,最
2x-y=5 ②
好的变式是( )
A.由①得x= B.由①得y=
C.由②得x= D.由②得y=2x-5
4.解方程组 3m-4n=7 ① 的最佳方法是( )
9m-10n+25=0②
A.由①得m= ,再代入②
B.由②得m= ,再代入①
C.由①得3m=7+4n,再代入②
D.由②得9m=10n-25,再代入①5.以方程组 y=x+1 的解为坐标的点(x,y)在
y=-x+2
第_____象限。
6.已知代数式 4xa-1与-3x-by2a+b是同类项,那
么a、b的值分别是( )。
A. a=2 B. a=-2 C. a=-2 D. a=2
b=-1 b=1 b=-1 b=1
7.已知方程组 x+2y=5 的解使等式2x+y=1成立,
4x-3y=4+a
求a的值。
8.已知二元一次方程组 x-2y=3的解x、y互为相
4x+3y=m-1
反数,求m的值。
9.已知 +(4x+3y-8)2=0,求xy的值。
10.如果∣y + 3x - 2∣+∣5x + 2y -2∣=0,
求 x 、y的 值.例2
根据市场调查,某种消毒液的大瓶装(500g)和小瓶装(250g)两种产品的销售数量(按瓶计算)的比为 .某厂每天生产这种消毒液 22.5吨,这些消毒液应该分装大、小瓶两种产品各多少瓶?
分析:
问题中包含两个等量关系式:
大瓶数:小瓶数=2:5
大瓶所装消毒液+小瓶所装消毒液=总生产量解:设这些消毒液应该分装x大瓶、y小瓶.由题意得③解得 x=20000把x=20000代入③,得 y=50000答:这些消毒液应该分装20000大瓶和50000小瓶.把③代入②,得由①,得小结:
①代入法可以解未知数系数为土1的,
②可解缺常数项的二元一次方程组,
③任意的二元一次方程组都可以用代入法解。练习:
1.有48支队520名运动员参加篮球、排球比赛,其
中每支篮球队10人,每支排球队12人,每名运动
员只能参加一项比赛,篮球、排球队各有多少支
参赛?
2.张翔从学校出发骑自行车去县城,中途因道路施
工步行一段路,1.5h后到达县城。他骑车的平均
速度是15km/h,步行的平均速度是5km/h,路程全
长20km.他骑车与步行各用多少时间?拓展:用整体代入法解二元一次方程组
例 用代入法解方程组 5x+6y=13 ①
7x+18y=-1②
练习:
用代入法解方程组。
(1)3x+2y=-2 (2)3x+2y-2=0
7x+4y=-2 -2x=-
例 用代入法解方程组解:由①,得 5(x-2)=3(y+4)5x-10=3y+125x-3y=22③②① ① 例 用代入法解方程组 ②解:令 = k,则x=3k+2,③y=5k-4,④把③、④代入②,得2(3k+2)-7(5k-4)=90解得 k=-2把k=-2代入③、④,得 X=-4,y=-14∴原方程组的解是5x-2y=-1练习:1.2.甲、乙两人同时解方程组 mx+y=5,甲看错了m,
2x-ny=13
解出的结果是 x=3.5,乙看错了n,解出的结果
y=-2
是 x=3,假设他们不再有其他错误,你能求出原
y=-7
方程组的解吗?3.甲、乙两人同求方程ax-by=7的整数解,甲求出
的一组解为 x=3,而乙把ax-by=7中的7错看成1,
y=4
求得一组解为 x=1,试求a、b的值。
y=2
4.一种蔬菜加工后出售,单价可提高20%,但质量
减少10%。现有未加工的这种蔬菜30千克,加工
后可以比不加工多卖12元,则这种蔬菜加工前和
加工后每千克各卖多少元?设这种蔬菜加工前每
千克x元,加工后每千克卖y元,跟具题意,所列
方程组正确的是( )
A. y=(1+20%)x B. y=(1+20%)x
30(1+10%)y-30x=12 30(1-10%)y-30x=12
C. y=(1-20%)x D.y=(1-20%)x
30(1-10%)y-30x=12 30(1+10%)y-30x=12
5.如图所示,将长方形ABCD的一个角折叠,折
痕为AE,∠BAD比∠BAE大48°.设∠BAE和∠BAD
的度数分别为x ,y度,那么x,y所适合的一个方程
组是( ) ABCD6.为了研究吸烟是否对肺癌有影响,某肿瘤研究所
随机地调查了10000人,并进行统计分析,结果
显示:在吸烟者中患肺癌的比例是2.5%,在不吸
烟者中患肺癌的比例是0.5%,吸烟者患肿瘤的人
数比不吸烟者患肺癌的人数多22人,那么这
10000人中,吸烟者与不吸烟者的患肺癌的人数
各是多少?7.将一摞笔记本分给若干同学,每个同学6本,则
剩下9本;每个同学8本,又差了3本,问共有多
少本笔记本?多少个同学?
8.一辆汽车从A地驶往B地,前路段为普通公路,其
余路段为高速公路,已知汽车在普通公路上行驶
的速度为60km/h,在高速公路上行驶的速度为
100km/h,汽车从A地到B地一共行驶2.2h。请你
根据以上信息,就该汽车行驶的“路程”或“时
间”,提出一个用二元一次方程组解决的问题,
并写出解答过程。9.某同学在A、B两家超市发现他看中的英语学习机
的单价相同,书包单价也相同,英语学习机和书
包单价之和是452元,且英语学习机的单价比书
包单价的4倍少8元。
(1)求该同学看中的英语学习机和书包单价各是
多少元?
(2)某一天该同学上街,恰好赶上商家促销,超
市A所有商品打7.5折销售,超市B全场购物满
100元返购物券30元销售(不足100元不返券,
购物券全场通用)。但他只带了400元钱,如
果他只在一家超市购买看中的英语学习机与
书包,那么在哪一家购买更省钱?谢谢指导!
——用代入法解二元一次方程组 “一切问题都可以转化为数学问题,一切数学问题都可以转化为代数问题,而一切代数问题又都可以转化为方程问题,因此,一旦解决了方程问题,一切问题将迎刃而解!”
——法国数学家 笛卡儿[Descartes, 1596-1650 ]名人语录
1、会用代入法解二元一次方程组。
2、体会解二元一次方程组的基本思想—“消元”。
确立目标 问题1:什么是二元一次方程?含有两个未知数,并且所含未知数的项的次数都是1的方程叫做二元一次方程。问题4:什么是二元一次方程组的解?问题2:什么是二元一次方程组?把具有相同未知数的两个二元一次方程合在一起,
就组成了一个二元一次方程组。 二元一次方程组的两个方程的公共解,叫做二元
一次方程组的解。
回顾与思考 问题3:什么是二元一次方程的解?使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解.1. 把下列方程写成用含x的式子表示y的形式.(2)课前热身 2.你能把上面两个方程写成用含y的式子表示x的形式?
(1)(1)(2)3.如何解这样的方程组探究 x + y = 200y = x + 10x克10克(x+10)x +( x +10) = 200①②x = 95y = 105 求方程组解的过程叫做解方程组转化探究 解二元一次方程组一元一次方程二元一次方程组消 元用代入法转化将未知数的个数由多化少,逐一解决的想法,
叫做消元思想。将二元一次方程组中一个方程的一个未知数用含另一未知数的式子表示出来,再代入另一个方程,实现消元,进而求得这个二元一次方程组的解。这种方法叫做代入消元法,简称代入法。概念巩固:
1.将未知数的个数由多化少,逐一解决的想法,
叫做______思想。2.将二元一次方程组中一个方程的一个未知数用含
_____未知数的式子表示出来,再_____另一个
方程,实现消元,进而求得这个二元一次方程组
的解。这种方法叫做_______,简称_____。解:①②把②代入①得:2y – 3(y – 1)= 1 y = 2把y = 2代入②,得x = y – 1 = 2 – 1 = 12 y – 3 x = 1x = y - 1(y-1)谈谈思路 例2 解方程组解:由①得:x = 3+y③把③代入②得:3(3+y)–8y= 141、将方程组里的一个方程变 形,用含有一个未知数的式子表示另一个未知数;2、用这个式子代替另一个方程中相应的未知数,得到一个一元一次方程。4、把这个未知数的值代入上面的式子,求得另一个未知数的值;5、写出方程组的解。变形代入求解写解解这个方程,得y= – 1把y= – 1代入③,得x = 3+(-1)=2回代3.解这个一元一次方程,
求得一个未知数的值;
一元一次方程二元一次方程组消 元转化代入法一般使用于未知数的系数是土1的。点拔:
灵活选择要表示的未知数,一般选择系数较简单的那个方程进行转化。
1.把下列方程写成用含x的式子表示y的形式。
①2x-y=3 ②3x+y-1=0 ③3x+2y=10
2.用代入法解二元一次方程组.
(1) (2) (3)练一练
(4)2a=1-b (5) + =
5a+3b=4 2(x-5)+(y+5)=-23.用代入法解二元一次方程组 3x+4y=2 ①时,最
2x-y=5 ②
好的变式是( )
A.由①得x= B.由①得y=
C.由②得x= D.由②得y=2x-5
4.解方程组 3m-4n=7 ① 的最佳方法是( )
9m-10n+25=0②
A.由①得m= ,再代入②
B.由②得m= ,再代入①
C.由①得3m=7+4n,再代入②
D.由②得9m=10n-25,再代入①5.以方程组 y=x+1 的解为坐标的点(x,y)在
y=-x+2
第_____象限。
6.已知代数式 4xa-1与-3x-by2a+b是同类项,那
么a、b的值分别是( )。
A. a=2 B. a=-2 C. a=-2 D. a=2
b=-1 b=1 b=-1 b=1
7.已知方程组 x+2y=5 的解使等式2x+y=1成立,
4x-3y=4+a
求a的值。
8.已知二元一次方程组 x-2y=3的解x、y互为相
4x+3y=m-1
反数,求m的值。
9.已知 +(4x+3y-8)2=0,求xy的值。
10.如果∣y + 3x - 2∣+∣5x + 2y -2∣=0,
求 x 、y的 值.例2
根据市场调查,某种消毒液的大瓶装(500g)和小瓶装(250g)两种产品的销售数量(按瓶计算)的比为 .某厂每天生产这种消毒液 22.5吨,这些消毒液应该分装大、小瓶两种产品各多少瓶?
分析:
问题中包含两个等量关系式:
大瓶数:小瓶数=2:5
大瓶所装消毒液+小瓶所装消毒液=总生产量解:设这些消毒液应该分装x大瓶、y小瓶.由题意得③解得 x=20000把x=20000代入③,得 y=50000答:这些消毒液应该分装20000大瓶和50000小瓶.把③代入②,得由①,得小结:
①代入法可以解未知数系数为土1的,
②可解缺常数项的二元一次方程组,
③任意的二元一次方程组都可以用代入法解。练习:
1.有48支队520名运动员参加篮球、排球比赛,其
中每支篮球队10人,每支排球队12人,每名运动
员只能参加一项比赛,篮球、排球队各有多少支
参赛?
2.张翔从学校出发骑自行车去县城,中途因道路施
工步行一段路,1.5h后到达县城。他骑车的平均
速度是15km/h,步行的平均速度是5km/h,路程全
长20km.他骑车与步行各用多少时间?拓展:用整体代入法解二元一次方程组
例 用代入法解方程组 5x+6y=13 ①
7x+18y=-1②
练习:
用代入法解方程组。
(1)3x+2y=-2 (2)3x+2y-2=0
7x+4y=-2 -2x=-
例 用代入法解方程组解:由①,得 5(x-2)=3(y+4)5x-10=3y+125x-3y=22③②① ① 例 用代入法解方程组 ②解:令 = k,则x=3k+2,③y=5k-4,④把③、④代入②,得2(3k+2)-7(5k-4)=90解得 k=-2把k=-2代入③、④,得 X=-4,y=-14∴原方程组的解是5x-2y=-1练习:1.2.甲、乙两人同时解方程组 mx+y=5,甲看错了m,
2x-ny=13
解出的结果是 x=3.5,乙看错了n,解出的结果
y=-2
是 x=3,假设他们不再有其他错误,你能求出原
y=-7
方程组的解吗?3.甲、乙两人同求方程ax-by=7的整数解,甲求出
的一组解为 x=3,而乙把ax-by=7中的7错看成1,
y=4
求得一组解为 x=1,试求a、b的值。
y=2
4.一种蔬菜加工后出售,单价可提高20%,但质量
减少10%。现有未加工的这种蔬菜30千克,加工
后可以比不加工多卖12元,则这种蔬菜加工前和
加工后每千克各卖多少元?设这种蔬菜加工前每
千克x元,加工后每千克卖y元,跟具题意,所列
方程组正确的是( )
A. y=(1+20%)x B. y=(1+20%)x
30(1+10%)y-30x=12 30(1-10%)y-30x=12
C. y=(1-20%)x D.y=(1-20%)x
30(1-10%)y-30x=12 30(1+10%)y-30x=12
5.如图所示,将长方形ABCD的一个角折叠,折
痕为AE,∠BAD比∠BAE大48°.设∠BAE和∠BAD
的度数分别为x ,y度,那么x,y所适合的一个方程
组是( ) ABCD6.为了研究吸烟是否对肺癌有影响,某肿瘤研究所
随机地调查了10000人,并进行统计分析,结果
显示:在吸烟者中患肺癌的比例是2.5%,在不吸
烟者中患肺癌的比例是0.5%,吸烟者患肿瘤的人
数比不吸烟者患肺癌的人数多22人,那么这
10000人中,吸烟者与不吸烟者的患肺癌的人数
各是多少?7.将一摞笔记本分给若干同学,每个同学6本,则
剩下9本;每个同学8本,又差了3本,问共有多
少本笔记本?多少个同学?
8.一辆汽车从A地驶往B地,前路段为普通公路,其
余路段为高速公路,已知汽车在普通公路上行驶
的速度为60km/h,在高速公路上行驶的速度为
100km/h,汽车从A地到B地一共行驶2.2h。请你
根据以上信息,就该汽车行驶的“路程”或“时
间”,提出一个用二元一次方程组解决的问题,
并写出解答过程。9.某同学在A、B两家超市发现他看中的英语学习机
的单价相同,书包单价也相同,英语学习机和书
包单价之和是452元,且英语学习机的单价比书
包单价的4倍少8元。
(1)求该同学看中的英语学习机和书包单价各是
多少元?
(2)某一天该同学上街,恰好赶上商家促销,超
市A所有商品打7.5折销售,超市B全场购物满
100元返购物券30元销售(不足100元不返券,
购物券全场通用)。但他只带了400元钱,如
果他只在一家超市购买看中的英语学习机与
书包,那么在哪一家购买更省钱?谢谢指导!
