苏教版(2019)选择性必修第一册《3.3 抛物线》2023年同步练习卷(含解析)
文档属性
| 名称 | 苏教版(2019)选择性必修第一册《3.3 抛物线》2023年同步练习卷(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 303.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-23 16:39:43 | ||
图片预览




文档简介
苏教版(2019)选择性必修第一册《3.3 抛物线》2023年同步练习卷
一、选择题
1.若抛物线y2=2px(p>0)上的点到其焦点的距离是点A到y轴距离的3倍,则p等于( )
A.2 B.4 C.6 D.8
2.已知抛物线C:y2=4x的焦点为F,过点F的直线与C交于M,N两点,若|MN|=10,则线段MN的中点到y轴的距离为( )
A.8 B.6 C.4 D.2
3.已知抛物线C:y2=8x的焦点为F,P为抛物线的准线上的一点,且P的纵坐标为正数,Q是直线PF与抛物线C的一个交点,若,则直线PF的方程为( )
A.x﹣y﹣2=0 B.x+y﹣2=0 C.x±y﹣2=0 D.不确定
4.如图,圆F:(x﹣1)2+y2=1和抛物线y2=4x,过F的直线与抛物线和圆依次交于A、B、C、D四点,求|AB| |CD|的值是( )
A.3 B.2 C.1 D.无法确定
5.已知:M={(x,y)|y≥x2},N{(x,y)|x2+(y﹣a)2≤1},则使M∩N=N成立的充要条件是( )
A.a≥ B. C.a≥1 D.0<a<1
二、多选题
(多选)6.已知抛物线C:y2=4x,O为坐标原点,点P为直线x=﹣2上一点,过点P作抛物线C的两条切线,切点分别为A,B,则( )
A.抛物线的焦点坐标为(0,1)
B.抛物线的准线方程为x=﹣1
C.直线AB一定过抛物线的焦点
D.OP⊥AB
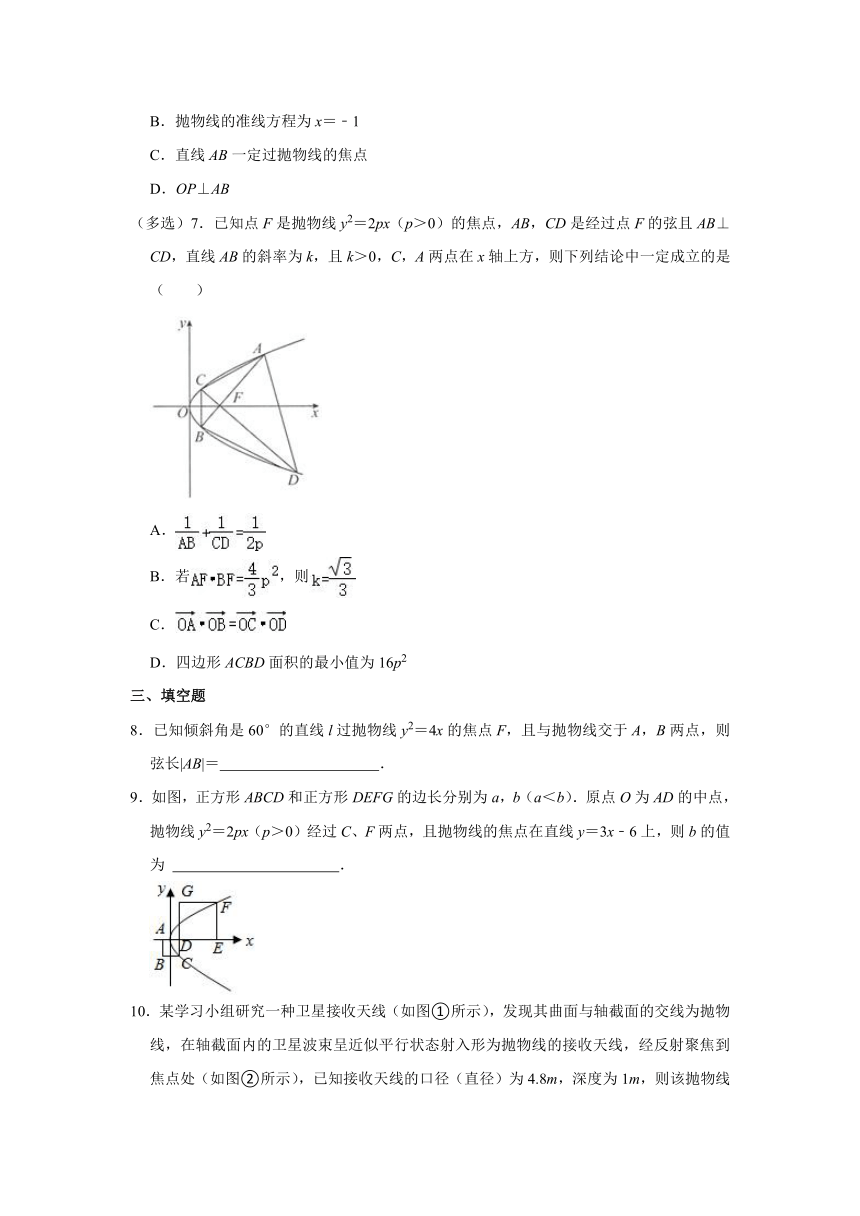
(多选)7.已知点F是抛物线y2=2px(p>0)的焦点,AB,CD是经过点F的弦且AB⊥CD,直线AB的斜率为k,且k>0,C,A两点在x轴上方,则下列结论中一定成立的是( )
A.
B.若,则
C.
D.四边形ACBD面积的最小值为16p2
三、填空题
8.已知倾斜角是60°的直线l过抛物线y2=4x的焦点F,且与抛物线交于A,B两点,则弦长|AB|= .
9.如图,正方形ABCD和正方形DEFG的边长分别为a,b(a<b).原点O为AD的中点,抛物线y2=2px(p>0)经过C、F两点,且抛物线的焦点在直线y=3x﹣6上,则b的值为 .
10.某学习小组研究一种卫星接收天线(如图①所示),发现其曲面与轴截面的交线为抛物线,在轴截面内的卫星波束呈近似平行状态射入形为抛物线的接收天线,经反射聚焦到焦点处(如图②所示),已知接收天线的口径(直径)为4.8m,深度为1m,则该抛物线的焦点到顶点的距离为 m.
11.已知F是抛物线C:y2=4x的焦点,P是抛物线在x轴上方一点,以P为圆心,|PF|为半径的圆被y轴截得的弦长为2,则圆P的方程为 .
四、解答题
12.已知抛物线y2=6x的弦AB过点P(4,2)且OA⊥OB(O为坐标原点),求弦AB的长.
13.已知过点A(4,4)的抛物线y2=2px的焦点为F,直线AF与抛物线的另一交点为B,点A关于x轴的对称点为A′.
(Ⅰ)求p的值;
(Ⅱ)求直线A′B与x轴交点的坐标.
14.已知抛物线E:y2=2px(p>0)恰好经过等腰梯形ABCD的四个顶点,AB∥CD,AD的延长线与抛物线E的准线的交点.
(1)求抛物线E的方程;
(2)证明:BD经过抛物线E的焦点.
15.已知过抛物线C:y2=2px(p>0)的焦点,斜率为的直线交抛物线于
(1)求该抛物线的方程;
(2)在抛物线C上求一点D,使得点D直线y=x+3的距离最短.
16.圆x2+y2=4上一点(x0,y0)处的切线交抛物线y2=8x于A,B两点,且满足∠AOB=90°,其中O为坐标原点,求x0.
苏教版(2019)选择性必修第一册《3.3 抛物线》2023年同步练习卷
参考答案与试题解析
一、选择题
1.【分析】根据抛物线的定义及题意可知3x0=x0+,得出x0求得p,可得答案.
【解答】解:由题意,3x0=x0+,∴x0=,
∴=32,
∵p>0,
∴p=8,
故选:D.
2.【分析】先根据抛物线方程求出p的值,再由抛物线的性质可得到答案.
【解答】解:∵抛物线y2=4x,∴p=2,
设经过点F的直线与抛物线相交于M,N两点,
其横坐标分别为x1,x2,利用抛物线定义,
MN中点横坐标为x0=(x1+x2)=(|MN|﹣p)=4,
则AB中点到y轴的距离是:4.
故选:C.
3.【分析】利用抛物线的定义,结合,P的纵坐标为正数求出直线的斜率,即可求出直线PF的方程.
【解答】解:抛物线y2=8x的焦点F(2,0),设Q到准线l的距离为d,则|QF|=d
∵,
∴||=d,
∵P的纵坐标为正数,
∴直线的倾斜角为135°,
∴直线的斜率为﹣1,
∴直线的方程为x+y﹣2=0.
故选:B.
4.【分析】可分两类讨论,若直线的斜率不存在,则直线方程为x=1,代入抛物线方程和圆的方程,可直接得到ABCD四个点的坐标,从而|AB||CD|=1.若直线的斜率存在,设为直线方程为y=k(x﹣1),不妨设A(x1,y1),D(x2,y2),过AB分别作抛物线准线的垂线,由抛物线的定义,|AF|=x1+1,|DF|=x2+1,把直线方程与抛物线方程联立,消去y可得k2x2﹣(2k2+4)x+k2=0,利用韦达定理及|AB|=|AF|﹣|BF|=x1,|CD|=|DF|﹣|CF|=x2,可求|AB||CD|的值.
【解答】解:若直线的斜率不存在,则直线方程为x=1,代入抛物线方程和圆的方程,可直接得到ABCD四个点的坐标为(1,2)(1,1)(1,﹣1)(1,﹣2),所以|AB|=1,|CD|=1,从而|AB||CD|=1.
若直线的斜率存在,设为k,因为直线过抛物线的焦点(1,0),则直线方程为y=k(x﹣1),
不妨设A(x1,y1),D(x2,y2),过AB分别作抛物线准线的垂线,由抛物线的定义,|AF|=x1+1,|DF|=x2+1,
把直线方程与抛物线方程联立,消去y可得k2x2﹣(2k2+4)x+k2=0,由韦达定理有 x1x2=1
而抛物线的焦点F同时是已知圆的圆心,所以|BF|=|CF|=R=1
从而有|AB|=|AF|﹣|BF|=x1,|CD|=|DF|﹣|CF|=x2.
所以|AB||CD|=x1x2=1
故选:C.
5.【分析】由题意确定E,F所表示的图形,及其几何意义:是a为何值时,动圆进入区域E,并被E所覆盖.然后根据已知条件解答即可.
【解答】解:∵E为抛物线y=x2的内部(包括周界),F为动圆x2+(y﹣a)2=1的内部(包括周界).该题的几何意义是a为何值时,动圆进入区域E,并被E所覆盖.
∵a是动圆圆心的纵坐标,显然结论应是a≥c(c∈R+),故可排除(B),(D),而当a=1时,E∩F≠F,(可验证点(0,1)到抛物线上点的最小距离为).
故选:A.
二、多选题
6.【分析】根据抛物线的焦点坐标和准线方程,结合一元二次方程根的判别式进行判断即可.
【解答】解:由题意可得F(1,0),抛物线的准线方程为x=﹣1,A错误,B正确;
设P(﹣2,m),显然直线PA存在斜率且不为零,设为k1,方程为y﹣m=k1(x+2),
与抛物线方程联立,得k1y2﹣4y+8k1+4m=0,
因为PA是该抛物线的切线,所以Δ=(﹣4)2﹣4k1(8k1+4m)=0,∴2+k1m﹣1=0,
且A的纵坐标为:﹣=,代入抛物线方程中可得A的横坐标为:,
设直线PB存在斜率且不为零,设为k2,
同理可得:2+k2m﹣1=0,且B的纵坐标为:﹣=,横坐标为,
k1、k2是方程2k2+km﹣1=0的两个不等实根,所以k1+k2=﹣,k1 k2=﹣,
因为kAB kOP= = = =﹣1,所以OP⊥AB,因此选项D正确:
由上可知:AB的斜率为,
直线AB的方程为:y﹣=(x﹣),∴y﹣2mk1=2x﹣2,由于2+k1m﹣1=0,∴k1m=1﹣2,
所以有(k1﹣2)y﹣2(1﹣2)=2x﹣2,∴(1﹣2)y=2k1(x﹣2),
所以直线AB一定过(2,0),显然该点不是抛物线的焦点,因此选项C不正确,
故选:BD.
7.【分析】由题意设直线AB的斜率,可得CD的斜率,设直线AB的方程,与抛物线联立求出两根之和,再由抛物线的性质到焦点的距离等于到准线的距离可得弦长|AB|的值,同理可得|CD|的值,进而可得+的值为定值,判断出A正确,
由抛物线的性质可得AF BF的表达式,将两根之和及两根之积代入,可得k的值为,判断出B不正确;
求出的数量积与斜率无关,可得的数量积与之相等,判断出C正确;
求出四边形ABCD的面积,由均值不等式可得面积的最小值,判断出D不正确.
【解答】解:由题意显然直线AB,CD的斜率存在且不为0
设直线AB的斜率为k,因为AB⊥CD,所以直线CD的斜率为﹣,
设A(x1,y1),B(x2,y2),由抛物线的方程可得焦点F(,0),
则直线AB的方程为y=k(x﹣),k>0,
联立,整理可得:k2x2﹣p(k2+2)+k2p2=0,
则x1+x2=p ,x1x2=p2,
所以弦长|AB|=x1+x2+p=p +p=;
同理可得:|CD|=2p(1+k2),
则有+=,故A正确;
B中,若,则(x1+)(x2+)=x1x2+(x1+x2)+=p2,
所以+ +=,解得k=,所以B不正确;
C中,=x1x2+y1y2=x1x2﹣2p=﹣2p =﹣p2,与斜率k无关,
同理可得=﹣p2,
故=,所以C正确;
S四边形ABCD=|AB| |CD|= 2p(1+k2)=2p2(k2++2)≥2p2(2+2)=8p2,
当且仅当k2=,即k=±1时取等号,所以D不正确;
故选:AC.
三、填空题
8.【分析】设A(x1,y1),B(x2,y2),利用抛物线的性质,求出|AB|=|AF|+|BF|=x1+x2+2,再结合韦达定理求出即可.
【解答】解:设A(x1,y1),B(x2,y2),A,B到准线的距离分别为dA,dB,
由抛物线的定义可知|AF|=dA=x1+1,|BF|=dB=x2+1,于是|AB|=|AF|+|BF|=x1+x2+2,
由已知得抛物线的焦点为F(1,0),斜率k=tan60°=,所以直线AB方程为y=(x﹣1),
将y=(x﹣1)代入方程y2=4x,化简得3x2﹣10x+3=0.
由求根公式得x1+x2=,于是|AB|=|AF|+|BF|=x1+x2+2=+2=,
故答案为:.
9.【分析】可先由图中的点与抛物线的位置关系,写出C,F两点的坐标,再将坐标代入抛物线方程中,消去参数p后,得到a,b的关系式,再根据抛物线的抛物线的焦点在直线y=3x﹣6上值求出p的值,问题得以解决.
【解答】解:由题可得C(,﹣a),F(+b,b),
则,
解得,
由抛物线的焦点在直线y=3x﹣6上,
∵焦点坐标为(,0),
∴0=﹣6,
解得p=4,
∴a=4,
∴b==4(+1)
故答案为:4(+1)
10.【分析】先设出抛物线的标准方程y2=2px(p>0),将点(1,2.4)代入抛物线方程求得p,进而求得抛物线的焦点到顶点的距离.
【解答】解:设抛物线方程为y2=2px(p>0),点(1,2.4)在抛物线y2=2px上,
∴2.42=2p×1.∴p=2.88,∴=1.44.
∴该抛物线的焦点到顶点的距离为1.44m.
故答案为:1.44.
11.【分析】推导出F(1,0),准线x=﹣1,设圆P与y轴交于M,N,且MN=2,圆P与准线x=﹣1相切于点A,连结AP,交MN于O,则AP=MP=r(r是圆P的半径),OA=1,OM=,由MP2=OP2+OM2,求出r=3,P(2,2),由上能求出圆P的方程.
【解答】解:∵F是抛物线C:y2=4x的焦点,P是抛物线在x轴上方一点,
∴F(1,0),准线x=﹣1,
P是抛物线在x轴上方一点,以P为圆心,|PF|为半径的圆被y轴截得的弦长为2,
则圆P与y轴交于M,N,且MN=2,圆P与准线x=﹣1相切于点A,
连结AP,交MN于O,则AP=MP=r(r是圆P的半径),
OA=1,OM=,
∵MP2=OP2+OM2,∴r2=(r﹣1)2+5,
解得r=3,∴P(2,2),
∴圆P的方程为(x﹣2)2+(y﹣2)2=9.
故答案为:(x﹣2)2+(y﹣2)2=9.
四、解答题
12.【分析】设出直线方程,与抛物线方程联立化为一元二次方程,利用根与系数的关系结合OA⊥OB,得到x1x2+y1y2=0从而求得k值,确定直线方程,求弦长.
【解答】解:直线AB的斜率一定存在,设为k(k≠0)
则AB方程为y﹣2=k(x﹣4),
y﹣2=k(x﹣4)与y2=6x联立消去x
整理得 ky2﹣6y+12﹣24k=0
设A(x1,y1),B(x2,y2)
∴y1y2=,
∵OA⊥OB
∴=0,即x1x2+y1y2=0
∴y1y2+()÷36=0
∵y1y2≠0
∴y1y2=﹣36
∴=﹣36,解得k=﹣1,
∴AB所在直线的方程为 y﹣2=﹣(x﹣4),即x+y﹣6=0,
所以弦AB的长==6.
13.【分析】(Ⅰ)由A的坐标满足抛物线的方程,解得p;
(Ⅱ)联立抛物线的方程和直线AF的方程,求得B的坐标,再求得A关于x轴的对称点A',可得直线A'B的方程,令y=0,可得所求交点的坐标.
【解答】解:(Ⅰ)把A(4,4)代入抛物线方程y2=2px,
可得16=8p,
解得p=2;
(Ⅱ)由(Ⅰ)知抛物线方程为y2=4x,且焦点F(1,0),
∴直线AF的方程为,即4x﹣3y﹣4=0,
与y2=4x联立,消去x得y2﹣3y﹣4=0,
解得y=4或﹣1,
∴B点的纵坐标为﹣1,代入y2=4x,得,
∴B(,﹣1),
而A(4,4)关于x轴的对称点A'(4,﹣4),
∴A'B的方程为,
当y=0时,x=﹣1,
所以直线A'B与x轴交点的坐标为(﹣1,0).
14.【分析】(1)由已知可得M为抛物线E的准线与对称轴的交点,从而求得p,则抛物线方程可求;
(2)分别设出A,B,D的坐标,再设出AD的方程,由抛物线方程联立,利用根与系数的关系可得A,D横坐标的乘积,设BD的方程,与抛物线方程联立,再由根与系数的关系可得BD与x轴的交点的横坐标,则结论得证.
【解答】(1)解:根据题意,为抛物线E的准线与对称轴的交点,
∴,则p=1,
∴抛物线E的方程为y2=2x;
(2)证明:设A(x1,y1),B(x1,﹣y1),D(x2,y2),
设直线AD的方程为y=k(x+),
联立方程组,得,
∴且0<x1<x2,∴x1<<x2.
设BD与x轴的交点坐标为(n,0)(n>0),直线BD的方程为y=,
与方程y2=2x联立,得.
解得,∴,即n=.
故BD经过抛物线E的焦点.
15.【分析】(1)设出直线AB的方程与y2=2px联立,结合:|AB|=x1+x2+p=,可求抛物线的方程;
(2)设D(x,y),求出点D直线y=x+3的距离,利用配方法求最值,即可得到结论.
【解答】解:(1)直线AB的方程是y=2(x﹣),与y2=2px联立,有4x2﹣5px+p2=0,
∴x1+x2=.
由抛物线定义得:|AB|=x1+x2+p=
∴p=2,∴抛物线方程是y2=4x.
(2)设D(x,y),则点D直线y=x+3的距离为==,
∴y=2时,点D直线y=x+3的距离最短为,此时D(1,2).
16.【分析】由圆上一点处的切线方程可得AB的方程,联立抛物线的方程,运用韦达定理和向量垂直的条件,化简整理解方程可得所求值.
【解答】解:圆x2+y2=4上一点(x0,y0)处的切线方程为x0x+y0y=4,
设A(x1,y1),B(x2,y2),联立可得+y0y﹣4=0,
可得y1y2=﹣,由∠AOB=90°,可得 =0,则x1x2+y1y2=0,
即 +y1y2= (﹣)2﹣=0,
解得x0=
一、选择题
1.若抛物线y2=2px(p>0)上的点到其焦点的距离是点A到y轴距离的3倍,则p等于( )
A.2 B.4 C.6 D.8
2.已知抛物线C:y2=4x的焦点为F,过点F的直线与C交于M,N两点,若|MN|=10,则线段MN的中点到y轴的距离为( )
A.8 B.6 C.4 D.2
3.已知抛物线C:y2=8x的焦点为F,P为抛物线的准线上的一点,且P的纵坐标为正数,Q是直线PF与抛物线C的一个交点,若,则直线PF的方程为( )
A.x﹣y﹣2=0 B.x+y﹣2=0 C.x±y﹣2=0 D.不确定
4.如图,圆F:(x﹣1)2+y2=1和抛物线y2=4x,过F的直线与抛物线和圆依次交于A、B、C、D四点,求|AB| |CD|的值是( )
A.3 B.2 C.1 D.无法确定
5.已知:M={(x,y)|y≥x2},N{(x,y)|x2+(y﹣a)2≤1},则使M∩N=N成立的充要条件是( )
A.a≥ B. C.a≥1 D.0<a<1
二、多选题
(多选)6.已知抛物线C:y2=4x,O为坐标原点,点P为直线x=﹣2上一点,过点P作抛物线C的两条切线,切点分别为A,B,则( )
A.抛物线的焦点坐标为(0,1)
B.抛物线的准线方程为x=﹣1
C.直线AB一定过抛物线的焦点
D.OP⊥AB
(多选)7.已知点F是抛物线y2=2px(p>0)的焦点,AB,CD是经过点F的弦且AB⊥CD,直线AB的斜率为k,且k>0,C,A两点在x轴上方,则下列结论中一定成立的是( )
A.
B.若,则
C.
D.四边形ACBD面积的最小值为16p2
三、填空题
8.已知倾斜角是60°的直线l过抛物线y2=4x的焦点F,且与抛物线交于A,B两点,则弦长|AB|= .
9.如图,正方形ABCD和正方形DEFG的边长分别为a,b(a<b).原点O为AD的中点,抛物线y2=2px(p>0)经过C、F两点,且抛物线的焦点在直线y=3x﹣6上,则b的值为 .
10.某学习小组研究一种卫星接收天线(如图①所示),发现其曲面与轴截面的交线为抛物线,在轴截面内的卫星波束呈近似平行状态射入形为抛物线的接收天线,经反射聚焦到焦点处(如图②所示),已知接收天线的口径(直径)为4.8m,深度为1m,则该抛物线的焦点到顶点的距离为 m.
11.已知F是抛物线C:y2=4x的焦点,P是抛物线在x轴上方一点,以P为圆心,|PF|为半径的圆被y轴截得的弦长为2,则圆P的方程为 .
四、解答题
12.已知抛物线y2=6x的弦AB过点P(4,2)且OA⊥OB(O为坐标原点),求弦AB的长.
13.已知过点A(4,4)的抛物线y2=2px的焦点为F,直线AF与抛物线的另一交点为B,点A关于x轴的对称点为A′.
(Ⅰ)求p的值;
(Ⅱ)求直线A′B与x轴交点的坐标.
14.已知抛物线E:y2=2px(p>0)恰好经过等腰梯形ABCD的四个顶点,AB∥CD,AD的延长线与抛物线E的准线的交点.
(1)求抛物线E的方程;
(2)证明:BD经过抛物线E的焦点.
15.已知过抛物线C:y2=2px(p>0)的焦点,斜率为的直线交抛物线于
(1)求该抛物线的方程;
(2)在抛物线C上求一点D,使得点D直线y=x+3的距离最短.
16.圆x2+y2=4上一点(x0,y0)处的切线交抛物线y2=8x于A,B两点,且满足∠AOB=90°,其中O为坐标原点,求x0.
苏教版(2019)选择性必修第一册《3.3 抛物线》2023年同步练习卷
参考答案与试题解析
一、选择题
1.【分析】根据抛物线的定义及题意可知3x0=x0+,得出x0求得p,可得答案.
【解答】解:由题意,3x0=x0+,∴x0=,
∴=32,
∵p>0,
∴p=8,
故选:D.
2.【分析】先根据抛物线方程求出p的值,再由抛物线的性质可得到答案.
【解答】解:∵抛物线y2=4x,∴p=2,
设经过点F的直线与抛物线相交于M,N两点,
其横坐标分别为x1,x2,利用抛物线定义,
MN中点横坐标为x0=(x1+x2)=(|MN|﹣p)=4,
则AB中点到y轴的距离是:4.
故选:C.
3.【分析】利用抛物线的定义,结合,P的纵坐标为正数求出直线的斜率,即可求出直线PF的方程.
【解答】解:抛物线y2=8x的焦点F(2,0),设Q到准线l的距离为d,则|QF|=d
∵,
∴||=d,
∵P的纵坐标为正数,
∴直线的倾斜角为135°,
∴直线的斜率为﹣1,
∴直线的方程为x+y﹣2=0.
故选:B.
4.【分析】可分两类讨论,若直线的斜率不存在,则直线方程为x=1,代入抛物线方程和圆的方程,可直接得到ABCD四个点的坐标,从而|AB||CD|=1.若直线的斜率存在,设为直线方程为y=k(x﹣1),不妨设A(x1,y1),D(x2,y2),过AB分别作抛物线准线的垂线,由抛物线的定义,|AF|=x1+1,|DF|=x2+1,把直线方程与抛物线方程联立,消去y可得k2x2﹣(2k2+4)x+k2=0,利用韦达定理及|AB|=|AF|﹣|BF|=x1,|CD|=|DF|﹣|CF|=x2,可求|AB||CD|的值.
【解答】解:若直线的斜率不存在,则直线方程为x=1,代入抛物线方程和圆的方程,可直接得到ABCD四个点的坐标为(1,2)(1,1)(1,﹣1)(1,﹣2),所以|AB|=1,|CD|=1,从而|AB||CD|=1.
若直线的斜率存在,设为k,因为直线过抛物线的焦点(1,0),则直线方程为y=k(x﹣1),
不妨设A(x1,y1),D(x2,y2),过AB分别作抛物线准线的垂线,由抛物线的定义,|AF|=x1+1,|DF|=x2+1,
把直线方程与抛物线方程联立,消去y可得k2x2﹣(2k2+4)x+k2=0,由韦达定理有 x1x2=1
而抛物线的焦点F同时是已知圆的圆心,所以|BF|=|CF|=R=1
从而有|AB|=|AF|﹣|BF|=x1,|CD|=|DF|﹣|CF|=x2.
所以|AB||CD|=x1x2=1
故选:C.
5.【分析】由题意确定E,F所表示的图形,及其几何意义:是a为何值时,动圆进入区域E,并被E所覆盖.然后根据已知条件解答即可.
【解答】解:∵E为抛物线y=x2的内部(包括周界),F为动圆x2+(y﹣a)2=1的内部(包括周界).该题的几何意义是a为何值时,动圆进入区域E,并被E所覆盖.
∵a是动圆圆心的纵坐标,显然结论应是a≥c(c∈R+),故可排除(B),(D),而当a=1时,E∩F≠F,(可验证点(0,1)到抛物线上点的最小距离为).
故选:A.
二、多选题
6.【分析】根据抛物线的焦点坐标和准线方程,结合一元二次方程根的判别式进行判断即可.
【解答】解:由题意可得F(1,0),抛物线的准线方程为x=﹣1,A错误,B正确;
设P(﹣2,m),显然直线PA存在斜率且不为零,设为k1,方程为y﹣m=k1(x+2),
与抛物线方程联立,得k1y2﹣4y+8k1+4m=0,
因为PA是该抛物线的切线,所以Δ=(﹣4)2﹣4k1(8k1+4m)=0,∴2+k1m﹣1=0,
且A的纵坐标为:﹣=,代入抛物线方程中可得A的横坐标为:,
设直线PB存在斜率且不为零,设为k2,
同理可得:2+k2m﹣1=0,且B的纵坐标为:﹣=,横坐标为,
k1、k2是方程2k2+km﹣1=0的两个不等实根,所以k1+k2=﹣,k1 k2=﹣,
因为kAB kOP= = = =﹣1,所以OP⊥AB,因此选项D正确:
由上可知:AB的斜率为,
直线AB的方程为:y﹣=(x﹣),∴y﹣2mk1=2x﹣2,由于2+k1m﹣1=0,∴k1m=1﹣2,
所以有(k1﹣2)y﹣2(1﹣2)=2x﹣2,∴(1﹣2)y=2k1(x﹣2),
所以直线AB一定过(2,0),显然该点不是抛物线的焦点,因此选项C不正确,
故选:BD.
7.【分析】由题意设直线AB的斜率,可得CD的斜率,设直线AB的方程,与抛物线联立求出两根之和,再由抛物线的性质到焦点的距离等于到准线的距离可得弦长|AB|的值,同理可得|CD|的值,进而可得+的值为定值,判断出A正确,
由抛物线的性质可得AF BF的表达式,将两根之和及两根之积代入,可得k的值为,判断出B不正确;
求出的数量积与斜率无关,可得的数量积与之相等,判断出C正确;
求出四边形ABCD的面积,由均值不等式可得面积的最小值,判断出D不正确.
【解答】解:由题意显然直线AB,CD的斜率存在且不为0
设直线AB的斜率为k,因为AB⊥CD,所以直线CD的斜率为﹣,
设A(x1,y1),B(x2,y2),由抛物线的方程可得焦点F(,0),
则直线AB的方程为y=k(x﹣),k>0,
联立,整理可得:k2x2﹣p(k2+2)+k2p2=0,
则x1+x2=p ,x1x2=p2,
所以弦长|AB|=x1+x2+p=p +p=;
同理可得:|CD|=2p(1+k2),
则有+=,故A正确;
B中,若,则(x1+)(x2+)=x1x2+(x1+x2)+=p2,
所以+ +=,解得k=,所以B不正确;
C中,=x1x2+y1y2=x1x2﹣2p=﹣2p =﹣p2,与斜率k无关,
同理可得=﹣p2,
故=,所以C正确;
S四边形ABCD=|AB| |CD|= 2p(1+k2)=2p2(k2++2)≥2p2(2+2)=8p2,
当且仅当k2=,即k=±1时取等号,所以D不正确;
故选:AC.
三、填空题
8.【分析】设A(x1,y1),B(x2,y2),利用抛物线的性质,求出|AB|=|AF|+|BF|=x1+x2+2,再结合韦达定理求出即可.
【解答】解:设A(x1,y1),B(x2,y2),A,B到准线的距离分别为dA,dB,
由抛物线的定义可知|AF|=dA=x1+1,|BF|=dB=x2+1,于是|AB|=|AF|+|BF|=x1+x2+2,
由已知得抛物线的焦点为F(1,0),斜率k=tan60°=,所以直线AB方程为y=(x﹣1),
将y=(x﹣1)代入方程y2=4x,化简得3x2﹣10x+3=0.
由求根公式得x1+x2=,于是|AB|=|AF|+|BF|=x1+x2+2=+2=,
故答案为:.
9.【分析】可先由图中的点与抛物线的位置关系,写出C,F两点的坐标,再将坐标代入抛物线方程中,消去参数p后,得到a,b的关系式,再根据抛物线的抛物线的焦点在直线y=3x﹣6上值求出p的值,问题得以解决.
【解答】解:由题可得C(,﹣a),F(+b,b),
则,
解得,
由抛物线的焦点在直线y=3x﹣6上,
∵焦点坐标为(,0),
∴0=﹣6,
解得p=4,
∴a=4,
∴b==4(+1)
故答案为:4(+1)
10.【分析】先设出抛物线的标准方程y2=2px(p>0),将点(1,2.4)代入抛物线方程求得p,进而求得抛物线的焦点到顶点的距离.
【解答】解:设抛物线方程为y2=2px(p>0),点(1,2.4)在抛物线y2=2px上,
∴2.42=2p×1.∴p=2.88,∴=1.44.
∴该抛物线的焦点到顶点的距离为1.44m.
故答案为:1.44.
11.【分析】推导出F(1,0),准线x=﹣1,设圆P与y轴交于M,N,且MN=2,圆P与准线x=﹣1相切于点A,连结AP,交MN于O,则AP=MP=r(r是圆P的半径),OA=1,OM=,由MP2=OP2+OM2,求出r=3,P(2,2),由上能求出圆P的方程.
【解答】解:∵F是抛物线C:y2=4x的焦点,P是抛物线在x轴上方一点,
∴F(1,0),准线x=﹣1,
P是抛物线在x轴上方一点,以P为圆心,|PF|为半径的圆被y轴截得的弦长为2,
则圆P与y轴交于M,N,且MN=2,圆P与准线x=﹣1相切于点A,
连结AP,交MN于O,则AP=MP=r(r是圆P的半径),
OA=1,OM=,
∵MP2=OP2+OM2,∴r2=(r﹣1)2+5,
解得r=3,∴P(2,2),
∴圆P的方程为(x﹣2)2+(y﹣2)2=9.
故答案为:(x﹣2)2+(y﹣2)2=9.
四、解答题
12.【分析】设出直线方程,与抛物线方程联立化为一元二次方程,利用根与系数的关系结合OA⊥OB,得到x1x2+y1y2=0从而求得k值,确定直线方程,求弦长.
【解答】解:直线AB的斜率一定存在,设为k(k≠0)
则AB方程为y﹣2=k(x﹣4),
y﹣2=k(x﹣4)与y2=6x联立消去x
整理得 ky2﹣6y+12﹣24k=0
设A(x1,y1),B(x2,y2)
∴y1y2=,
∵OA⊥OB
∴=0,即x1x2+y1y2=0
∴y1y2+()÷36=0
∵y1y2≠0
∴y1y2=﹣36
∴=﹣36,解得k=﹣1,
∴AB所在直线的方程为 y﹣2=﹣(x﹣4),即x+y﹣6=0,
所以弦AB的长==6.
13.【分析】(Ⅰ)由A的坐标满足抛物线的方程,解得p;
(Ⅱ)联立抛物线的方程和直线AF的方程,求得B的坐标,再求得A关于x轴的对称点A',可得直线A'B的方程,令y=0,可得所求交点的坐标.
【解答】解:(Ⅰ)把A(4,4)代入抛物线方程y2=2px,
可得16=8p,
解得p=2;
(Ⅱ)由(Ⅰ)知抛物线方程为y2=4x,且焦点F(1,0),
∴直线AF的方程为,即4x﹣3y﹣4=0,
与y2=4x联立,消去x得y2﹣3y﹣4=0,
解得y=4或﹣1,
∴B点的纵坐标为﹣1,代入y2=4x,得,
∴B(,﹣1),
而A(4,4)关于x轴的对称点A'(4,﹣4),
∴A'B的方程为,
当y=0时,x=﹣1,
所以直线A'B与x轴交点的坐标为(﹣1,0).
14.【分析】(1)由已知可得M为抛物线E的准线与对称轴的交点,从而求得p,则抛物线方程可求;
(2)分别设出A,B,D的坐标,再设出AD的方程,由抛物线方程联立,利用根与系数的关系可得A,D横坐标的乘积,设BD的方程,与抛物线方程联立,再由根与系数的关系可得BD与x轴的交点的横坐标,则结论得证.
【解答】(1)解:根据题意,为抛物线E的准线与对称轴的交点,
∴,则p=1,
∴抛物线E的方程为y2=2x;
(2)证明:设A(x1,y1),B(x1,﹣y1),D(x2,y2),
设直线AD的方程为y=k(x+),
联立方程组,得,
∴且0<x1<x2,∴x1<<x2.
设BD与x轴的交点坐标为(n,0)(n>0),直线BD的方程为y=,
与方程y2=2x联立,得.
解得,∴,即n=.
故BD经过抛物线E的焦点.
15.【分析】(1)设出直线AB的方程与y2=2px联立,结合:|AB|=x1+x2+p=,可求抛物线的方程;
(2)设D(x,y),求出点D直线y=x+3的距离,利用配方法求最值,即可得到结论.
【解答】解:(1)直线AB的方程是y=2(x﹣),与y2=2px联立,有4x2﹣5px+p2=0,
∴x1+x2=.
由抛物线定义得:|AB|=x1+x2+p=
∴p=2,∴抛物线方程是y2=4x.
(2)设D(x,y),则点D直线y=x+3的距离为==,
∴y=2时,点D直线y=x+3的距离最短为,此时D(1,2).
16.【分析】由圆上一点处的切线方程可得AB的方程,联立抛物线的方程,运用韦达定理和向量垂直的条件,化简整理解方程可得所求值.
【解答】解:圆x2+y2=4上一点(x0,y0)处的切线方程为x0x+y0y=4,
设A(x1,y1),B(x2,y2),联立可得+y0y﹣4=0,
可得y1y2=﹣,由∠AOB=90°,可得 =0,则x1x2+y1y2=0,
即 +y1y2= (﹣)2﹣=0,
解得x0=
