人教a版(2019)必修第一册《3.4 函数的应用(一)》2023年同步练习卷(含解析)
文档属性
| 名称 | 人教a版(2019)必修第一册《3.4 函数的应用(一)》2023年同步练习卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 153.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-23 16:47:02 | ||
图片预览



文档简介
人教A版(2019)必修第一册《3.4 函数的应用(一)》2023年同步练习卷
一、选择题
1.某产品的总成本y(单位:万元)与产量x(单位:台)之间的函数关系式为y=3000+20x﹣0.1x2(0<x<240,x∈N).若每台产品的售价为25万元,则生产者不亏本(销售收入不小于总成本)时的最低产量是( )
A.100台 B.120台 C.150台 D.180台
2.某公司招聘员工,面试人数按拟录用人数分段计算,计算公式为:y=,其中,x代表拟录用人数,y代表面试人数.若应聘面试的人数为60,则该公司拟录用人数为( )
A.15 B.40 C.25 D.130
3.随着海拔的升高,大气压强下降,空气中的含氧量也随之下降,且含氧量y(g/m3)与大气压强x(kPa)成正比例函数关系.当x=36时,y=144,则y与x的函数关系为( )
A.y=x B.y=x(x≥0)
C.y=4x D.y=4x(x≥0)
4.某商场将彩电的售价先按进价提高40%,然后“八折优惠”,结果每台彩电利润为360元,那么彩电的进价是( )
A.2000元 B.2500元 C.3000元 D.3500元
5.某桶装水经营部每天的房租、人员工资等固定成本为200元,每桶水的进价是5元.当销售单价为6元时,日均销售量为480桶.根据数据分析,销售单价在进价基础上每增加1元,日均销售量就减少40桶.为了使日均销售利润最大,销售单价应定为( )
A.6.5元 B.8.5元 C.10.5元 D.11.5元
6.李华经营了两家电动轿车销售连锁店.其月利润(单位:元)分别为L1=﹣5x2+900x﹣16000,L2=300x﹣2000(其中x为销售辆数).若某月两连锁店共销售了110辆.则能获得的最大利润为( )
A.11000元 B.22000元 C.33000元 D.40000元
7.某商场从生产厂家以每件20元的价格购进一批商品,若该商品零售价定为P元,销售量为Q,则销量Q(单位:件)与零售价P(单位:元)有如下关系:Q=8300﹣170P﹣P2,则最大毛利润为(毛利润=销售收入﹣进货支出)( )
A.30元 B.60元 C.28000元 D.23000元
8.把长为12cm的细铁丝截成两段,各自围成一个正三角形,那么这两个正三角形面积之和的最小值是( )
A.cm2 B.4cm2 C.3cm2 D.2cm2
二、多选题
(多选)9.甲、乙两人在一次赛跑中,从同一地点出发,路程S与时间t的函数关系如图所示,则下列说法正确的是( )
A.甲比乙先出发
B.乙比甲跑的路程一样多
C.甲、乙两人的速度相同
D.甲比乙先到达终点
(多选)10.某工厂八年来某种产品总产量y(即前x年年产量之和)与时间x(年)的函数关系如图,下列说法中正确的是( )
A.前三年中,总产量的增长速度越来越慢
B.前三年中,年产量的增长速度越来越慢
C.第三年后,这种产品停止生产
D.第三年后,年产量保持不变
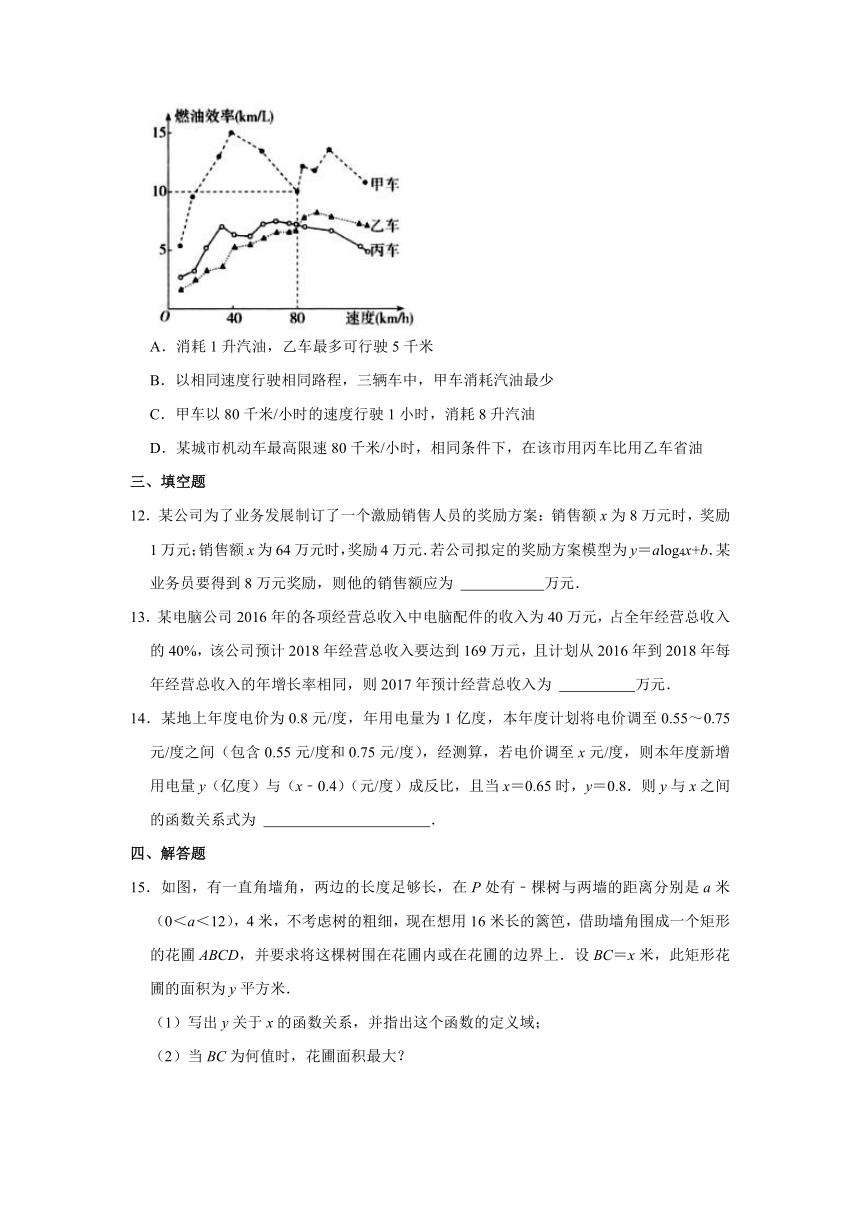
(多选)11.汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况,下列叙述中正确的是( )
A.消耗1升汽油,乙车最多可行驶5千米
B.以相同速度行驶相同路程,三辆车中,甲车消耗汽油最少
C.甲车以80千米/小时的速度行驶1小时,消耗8升汽油
D.某城市机动车最高限速80千米/小时,相同条件下,在该市用丙车比用乙车省油
三、填空题
12.某公司为了业务发展制订了一个激励销售人员的奖励方案:销售额x为8万元时,奖励1万元;销售额x为64万元时,奖励4万元.若公司拟定的奖励方案模型为y=alog4x+b.某业务员要得到8万元奖励,则他的销售额应为 万元.
13.某电脑公司2016年的各项经营总收入中电脑配件的收入为40万元,占全年经营总收入的40%,该公司预计2018年经营总收入要达到169万元,且计划从2016年到2018年每年经营总收入的年增长率相同,则2017年预计经营总收入为 万元.
14.某地上年度电价为0.8元/度,年用电量为1亿度,本年度计划将电价调至0.55~0.75元/度之间(包含0.55元/度和0.75元/度),经测算,若电价调至x元/度,则本年度新增用电量y(亿度)与(x﹣0.4)(元/度)成反比,且当x=0.65时,y=0.8.则y与x之间的函数关系式为 .
四、解答题
15.如图,有一直角墙角,两边的长度足够长,在P处有﹣棵树与两墙的距离分别是a米(0<a<12),4米,不考虑树的粗细,现在想用16米长的篱笆,借助墙角围成一个矩形的花圃ABCD,并要求将这棵树围在花圃内或在花圃的边界上.设BC=x米,此矩形花圃的面积为y平方米.
(1)写出y关于x的函数关系,并指出这个函数的定义域;
(2)当BC为何值时,花圃面积最大?
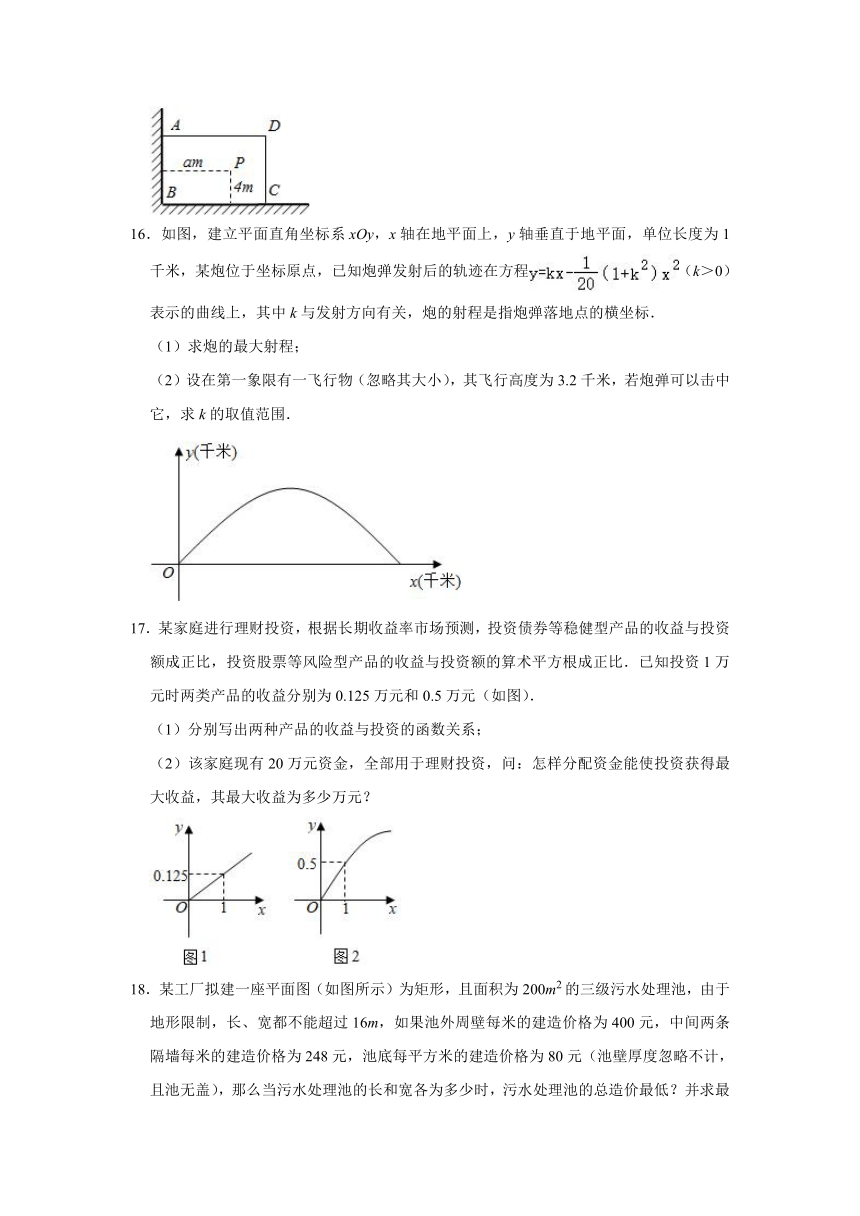
16.如图,建立平面直角坐标系xOy,x轴在地平面上,y轴垂直于地平面,单位长度为1千米,某炮位于坐标原点,已知炮弹发射后的轨迹在方程(k>0)表示的曲线上,其中k与发射方向有关,炮的射程是指炮弹落地点的横坐标.
(1)求炮的最大射程;
(2)设在第一象限有一飞行物(忽略其大小),其飞行高度为3.2千米,若炮弹可以击中它,求k的取值范围.
17.某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元和0.5万元(如图).
(1)分别写出两种产品的收益与投资的函数关系;
(2)该家庭现有20万元资金,全部用于理财投资,问:怎样分配资金能使投资获得最大收益,其最大收益为多少万元?
18.某工厂拟建一座平面图(如图所示)为矩形,且面积为200m2的三级污水处理池,由于地形限制,长、宽都不能超过16m,如果池外周壁每米的建造价格为400元,中间两条隔墙每米的建造价格为248元,池底每平方米的建造价格为80元(池壁厚度忽略不计,且池无盖),那么当污水处理池的长和宽各为多少时,污水处理池的总造价最低?并求最低总造价.
人教A版(2019)必修第一册《3.4 函数的应用(一)》2023年同步练习卷
参考答案与试题解析
一、选择题
1.【分析】由题意得到25x 3000+20x﹣0.1x2,又x∈(0,240),x∈N,即可求解.
【解答】解:由题意可知:要使企业不亏本则有总收入要大于等于总支出,
又因为总收入为:25x,
总支出为:3000+20x﹣0.1x2,
所以25x 3000+20x﹣0.1x2,
解得:x 150或x ﹣200,
又x∈(0,240),x∈N,
所以150 x<240,x∈N,
故能使生产者不亏本的最低产量是150台.
故选:C.
2.【分析】这是已知函数值求自变量的问题,又是分段函数,所以分类讨论求解即可.
【解答】解:令y=60,若4x=60,则x=15>10,不合题意;
若2x+10=60,则x=25,满足题意;
若1.5x=60,则x=40<100,不合题意.
故拟录用人数为25.
故选:C.
3.【分析】设y=kx,把x=36,y=144代入可求得k值,然后可求得答案.
【解答】解:设y=kx,把x=36,y=144代入得k=4,
∴y与x的函数关系为:y=4x(x≥0).
故选:D.
4.【分析】设彩电的进价是x元,由题意列出方程:x(1+40%)×0.8=360+x,由此能求出结果.
【解答】解:设彩电的进价是x元,
由题意得:x(1+40%)×0.8=360+x,
解得x=3000.
故选:C.
5.【分析】若设定价在进价的基础上增加x元,日销售利润为y元,则y=x[480﹣40(x﹣1)]﹣200,其中0<x<13,整理函数y,可得x取何值时,y有最大值,即获得最大利润
【解答】解:设定价在进价的基础上增加x元,日销售利润为y元,则
y=x[480﹣40(x﹣1)]﹣200,
由于x>0,且520﹣40x>0,所以,0<x<13;
即y=﹣40x2+520x﹣200,0<x<13.
所以,当x=﹣=6.5时,y取最大值.
此时售价为6.5+5=11.5
故选:D.
6.【分析】先根据题意,可设一其中一家连锁店销售x辆,则另一家销售(110﹣x)辆,再列出总利润S的表达式,是一个关于x的二次函数,最后求此二次函数的最大值即可.
【解答】解析:依题意,可设一其中一家连锁店销售x辆,则另一家销售(110﹣x)辆,
∴总利润S=﹣5x2+900x﹣16000+300(110﹣x)﹣2000
=﹣5x2+600x+15000(x≥0).
∴当x=60时,S取最大值.
且为Smax=33000.
故选:C.
7.【分析】毛利润等于销售额减去成本,可建立函数关系式,利用导数可求函数的极值点,利用极值就是最值,可得结论.
【解答】解:由题意知:毛利润等于销售额减去成本,即
L(P)=PQ﹣20Q=Q(P﹣20)=(8300﹣170P﹣P2)(P﹣20)
=﹣P3﹣150P2+11700P﹣166000,
所以L′(P)=﹣3P2﹣300P+11700.
令L′(P)=0,解得P=30或P=﹣130(舍去).
此时,L(30)=23000.
因为在P=30附近的左侧L′(P)>0,右侧L′(P)<0.
所以L(30)是极大值,根据实际问题的意义知,L(30)是最大值,
故选:D.
8.【分析】设两段长分别为xcm,(12﹣x)cm,则这两个正三角形面积之和 S=()2+()2,
利用二次函数的性质求出其最小值.
【解答】解:设两段长分别为xcm,(12﹣x)cm,
则这两个正三角形面积之和 S=()2+()2
=(x2﹣12x+72)=[(x﹣6)2+36]≥2,
故选:D.
二、多选题
9.【分析】根据路程和时间关系图,判断甲乙两人的速度,时间关系进行判断即可.
【解答】解:当t=0时,甲乙都在原点,说明甲乙两人是同时出发,故A错误,
甲乙两人最后的最大值相同,则甲乙两人路程一样多,故B正确,
甲到达的时间短,乙到达的时间长,则甲的速度对,乙的速度慢,即甲先到终点,故C错误,D正确,
故选:BD.
10.【分析】根据图象可分析产量的变化情况,前三年增长变慢,后五年停止生产.
【解答】解:在区间[0,3]上,函数图象在任一点处的切线斜率越来越小,表明总产量的增长速度越来越慢,即选项A正确;
由总产量增长越来越慢知,年产量逐年减少,即选项B错误;
在区间[3,8]上,图象呈水平直线,表明总产量保持不变,即年产量为0,因此选项C和D均正确.
故选:ACD.
11.【分析】结合燃油效率情况图依次分析各个选项即可.
【解答】解:对于A,消耗1升汽油,乙车最多可行驶距离大于5千米,故A错误;
对于B,因为当速度相同时,甲的燃油效率最高,所以以相同速度行驶相同路程,三辆车中,甲车消耗汽油最少,故B正确;
对于C,甲车以80千米/小时的速度行驶1小时,此时的燃油效率是10km/L,一共开了80km,所以消耗8升汽油,故C正确;
对于D,当速度小于80千米/小时时,丙车的燃油效率比乙车高,所以相同条件下,在该市用丙车比用乙车省油,故D正确.
故选:BCD.
三、填空题
12.【分析】把点(8,1),(64,4)代入y=alog4x+b,得到关于a,b的方程组,求得a与b的值,可得函数解析式,取y=8,求解对数方程得x值即可.
【解答】解:函数模型为y=alog4x+b,把点(8,1),(64,4)代入,
可得,解得a=2,b=﹣2.
∴y=2log4x﹣2,
由2log4x﹣2=8,得2log4x=10,即log2x=10,得x=210=1024.
∴某业务员要得到8万元奖励,则他的销售额应为1024万元.
故答案为:1024.
13.【分析】增长率问题的一般形式为a(1+x)2=b,a为起始时间的有关数量,b为终止时间的有关数量.本题中a就是2016年的经营收入,b就是2018年的经营收入,从而可求出增长率的值,进而可求2017年预计经营总收入.
【解答】解:2016年的经营总收入为400÷40%=1000(万元).
设年增长率为x(x>0),依题意得,1000(1+x)2=169,
解得:x1=0.3,x2=﹣2.3,
∵x>0
∴x2=﹣2.3不合题意,
∴只取x1=0.3.
1000(1+x)=1000×1.3=130(万元).
即2017年预计经营总收入为130万元.
故答案为:130.
14.【分析】设,把x=0.65,y=0.8代入可得关于k的方程,解出k即可得答案.
【解答】解:因为y与x﹣0.4成反比例,设,
把x=0.65,y=0.8代入得,
解得k=0.2.
所以y与x之间的函数关系式为.
故答案为:.
四、解答题
15.【分析】(1)要使树被圈进去,则ABCD中BC≥a,CD≥4,由此可确定函数的变量的范围.设长BC=x米,宽CD=(16﹣x)米,所以面积y=f(x)=x(16﹣x)=﹣x2+16x;
(2)由(1)得,y=f(x)=﹣x2+16x=﹣(x﹣8)2+64,x∈[a,12],由于对称轴x=8,根据0<a<12,故要进行分类讨论:即8≤a<12;4≤a<8;0<a<4,从而可求y=f(x)的最大值.
【解答】解:(1)要使树被圈进去,则ABCD中BC≥a,CD≥4,
因为篱笆长为16米,所以当长BC=x米时,宽CD=(16﹣x)米.
由于BC≥a,CD≥4,故a≤x≤12,
所以面积y=f(x)=x(16﹣x)=﹣x2+16x,其定义域为x∈[a,12];
(2)由(1)得,y=f(x)=﹣x2+16x=﹣(x﹣8)2+64,x∈[a,12]
对称轴x=8,又因为0<a<12,
所以,当8≤a<12时,x=a时,ymax=﹣a2+16a;
当4≤a<8时,x=8时,ymax=64;
当0<a<4时,x=8时,ymax=64.
16.【分析】(1)令=0,则x=或0(舍0),再利用基本不等式的性质求出x的最大值即可;
(2)原问题等价于存在x>0,使得y=kx﹣(1+k2)x2=3.2成立,即关于x的方程(k2+1)x2﹣20kx+64=0有正根,然后利用韦达定理列出关于k的不等式,解之即可.
【解答】解:(1)令=0,则x=0或,
∵k>0,x>0,
∴x==≤=10,当且仅当=k,即k=1时,等号成立.
故当k=1时,炮的射程最大,为10千米.
(2)炮弹可以击中目标等价于存在x>0,使得y=kx﹣(1+k2)x2=3.2成立,
即关于x的方程(k2+1)x2﹣20kx+64=0有正根,
由韦达定理知,满足两根之和大于0,两根之积大于0,
∴只需Δ=(20k)2﹣4(k2+1)×64≥0,解得k≥或k≤﹣.
∵k>0,∴k≥.
故若炮弹可以击中它,k的取值范围为.
17.【分析】(1)由投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比,结合函数图象,我们可以利用待定系数法来求两种产品的收益与投资的函数关系;
(2)由(1)的结论,我们设投资债券类产品x万元,则股票类投资为20﹣x万元.这时可以构造出一个关于收益y的函数,然后利用求函数最大值的方法进行求解.
【解答】解:(1)f(x)=k1x,,
,,(x≥0),
(x≥0)
(2)设:投资债券类产品x万元,则股票类投资为20﹣x万元.
(0≤x≤20)
令,则==
所以当t=2,即x=16万元时,收益最大,ymax=3万元.
则投资债券等稳健型产品16万元,投资股票等风险型产品4万元获得收益最大,最大收益为3万元.
18.【分析】设污水处理池的长为x米,可得宽为米,列出总造价Q(x)=400(2x+2×)+248×2×+80×200,再根据对勾函数的单调性,即可求出最值.
【解答】解:设污水处理池的长为x米,则宽为米(0<x≤16,0<≤16),
∴12.5≤x≤16.
于是总造价Q(x)=400(2x+2×)+248×2×+80×200.
=800(x+)+16 000,
由对勾函数的性质可知y=x+在(0,18)上单调递减,在(18,+∞)上单调递增,
∴Q(x)在[12.5,16]上是单调递减函数,
∴Q(x)≥Q(16)=45000.
所以当污水处理池的长为16米,宽为12.5米时,总造价最低,最低造价为45 000元.
一、选择题
1.某产品的总成本y(单位:万元)与产量x(单位:台)之间的函数关系式为y=3000+20x﹣0.1x2(0<x<240,x∈N).若每台产品的售价为25万元,则生产者不亏本(销售收入不小于总成本)时的最低产量是( )
A.100台 B.120台 C.150台 D.180台
2.某公司招聘员工,面试人数按拟录用人数分段计算,计算公式为:y=,其中,x代表拟录用人数,y代表面试人数.若应聘面试的人数为60,则该公司拟录用人数为( )
A.15 B.40 C.25 D.130
3.随着海拔的升高,大气压强下降,空气中的含氧量也随之下降,且含氧量y(g/m3)与大气压强x(kPa)成正比例函数关系.当x=36时,y=144,则y与x的函数关系为( )
A.y=x B.y=x(x≥0)
C.y=4x D.y=4x(x≥0)
4.某商场将彩电的售价先按进价提高40%,然后“八折优惠”,结果每台彩电利润为360元,那么彩电的进价是( )
A.2000元 B.2500元 C.3000元 D.3500元
5.某桶装水经营部每天的房租、人员工资等固定成本为200元,每桶水的进价是5元.当销售单价为6元时,日均销售量为480桶.根据数据分析,销售单价在进价基础上每增加1元,日均销售量就减少40桶.为了使日均销售利润最大,销售单价应定为( )
A.6.5元 B.8.5元 C.10.5元 D.11.5元
6.李华经营了两家电动轿车销售连锁店.其月利润(单位:元)分别为L1=﹣5x2+900x﹣16000,L2=300x﹣2000(其中x为销售辆数).若某月两连锁店共销售了110辆.则能获得的最大利润为( )
A.11000元 B.22000元 C.33000元 D.40000元
7.某商场从生产厂家以每件20元的价格购进一批商品,若该商品零售价定为P元,销售量为Q,则销量Q(单位:件)与零售价P(单位:元)有如下关系:Q=8300﹣170P﹣P2,则最大毛利润为(毛利润=销售收入﹣进货支出)( )
A.30元 B.60元 C.28000元 D.23000元
8.把长为12cm的细铁丝截成两段,各自围成一个正三角形,那么这两个正三角形面积之和的最小值是( )
A.cm2 B.4cm2 C.3cm2 D.2cm2
二、多选题
(多选)9.甲、乙两人在一次赛跑中,从同一地点出发,路程S与时间t的函数关系如图所示,则下列说法正确的是( )
A.甲比乙先出发
B.乙比甲跑的路程一样多
C.甲、乙两人的速度相同
D.甲比乙先到达终点
(多选)10.某工厂八年来某种产品总产量y(即前x年年产量之和)与时间x(年)的函数关系如图,下列说法中正确的是( )
A.前三年中,总产量的增长速度越来越慢
B.前三年中,年产量的增长速度越来越慢
C.第三年后,这种产品停止生产
D.第三年后,年产量保持不变
(多选)11.汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况,下列叙述中正确的是( )
A.消耗1升汽油,乙车最多可行驶5千米
B.以相同速度行驶相同路程,三辆车中,甲车消耗汽油最少
C.甲车以80千米/小时的速度行驶1小时,消耗8升汽油
D.某城市机动车最高限速80千米/小时,相同条件下,在该市用丙车比用乙车省油
三、填空题
12.某公司为了业务发展制订了一个激励销售人员的奖励方案:销售额x为8万元时,奖励1万元;销售额x为64万元时,奖励4万元.若公司拟定的奖励方案模型为y=alog4x+b.某业务员要得到8万元奖励,则他的销售额应为 万元.
13.某电脑公司2016年的各项经营总收入中电脑配件的收入为40万元,占全年经营总收入的40%,该公司预计2018年经营总收入要达到169万元,且计划从2016年到2018年每年经营总收入的年增长率相同,则2017年预计经营总收入为 万元.
14.某地上年度电价为0.8元/度,年用电量为1亿度,本年度计划将电价调至0.55~0.75元/度之间(包含0.55元/度和0.75元/度),经测算,若电价调至x元/度,则本年度新增用电量y(亿度)与(x﹣0.4)(元/度)成反比,且当x=0.65时,y=0.8.则y与x之间的函数关系式为 .
四、解答题
15.如图,有一直角墙角,两边的长度足够长,在P处有﹣棵树与两墙的距离分别是a米(0<a<12),4米,不考虑树的粗细,现在想用16米长的篱笆,借助墙角围成一个矩形的花圃ABCD,并要求将这棵树围在花圃内或在花圃的边界上.设BC=x米,此矩形花圃的面积为y平方米.
(1)写出y关于x的函数关系,并指出这个函数的定义域;
(2)当BC为何值时,花圃面积最大?
16.如图,建立平面直角坐标系xOy,x轴在地平面上,y轴垂直于地平面,单位长度为1千米,某炮位于坐标原点,已知炮弹发射后的轨迹在方程(k>0)表示的曲线上,其中k与发射方向有关,炮的射程是指炮弹落地点的横坐标.
(1)求炮的最大射程;
(2)设在第一象限有一飞行物(忽略其大小),其飞行高度为3.2千米,若炮弹可以击中它,求k的取值范围.
17.某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元和0.5万元(如图).
(1)分别写出两种产品的收益与投资的函数关系;
(2)该家庭现有20万元资金,全部用于理财投资,问:怎样分配资金能使投资获得最大收益,其最大收益为多少万元?
18.某工厂拟建一座平面图(如图所示)为矩形,且面积为200m2的三级污水处理池,由于地形限制,长、宽都不能超过16m,如果池外周壁每米的建造价格为400元,中间两条隔墙每米的建造价格为248元,池底每平方米的建造价格为80元(池壁厚度忽略不计,且池无盖),那么当污水处理池的长和宽各为多少时,污水处理池的总造价最低?并求最低总造价.
人教A版(2019)必修第一册《3.4 函数的应用(一)》2023年同步练习卷
参考答案与试题解析
一、选择题
1.【分析】由题意得到25x 3000+20x﹣0.1x2,又x∈(0,240),x∈N,即可求解.
【解答】解:由题意可知:要使企业不亏本则有总收入要大于等于总支出,
又因为总收入为:25x,
总支出为:3000+20x﹣0.1x2,
所以25x 3000+20x﹣0.1x2,
解得:x 150或x ﹣200,
又x∈(0,240),x∈N,
所以150 x<240,x∈N,
故能使生产者不亏本的最低产量是150台.
故选:C.
2.【分析】这是已知函数值求自变量的问题,又是分段函数,所以分类讨论求解即可.
【解答】解:令y=60,若4x=60,则x=15>10,不合题意;
若2x+10=60,则x=25,满足题意;
若1.5x=60,则x=40<100,不合题意.
故拟录用人数为25.
故选:C.
3.【分析】设y=kx,把x=36,y=144代入可求得k值,然后可求得答案.
【解答】解:设y=kx,把x=36,y=144代入得k=4,
∴y与x的函数关系为:y=4x(x≥0).
故选:D.
4.【分析】设彩电的进价是x元,由题意列出方程:x(1+40%)×0.8=360+x,由此能求出结果.
【解答】解:设彩电的进价是x元,
由题意得:x(1+40%)×0.8=360+x,
解得x=3000.
故选:C.
5.【分析】若设定价在进价的基础上增加x元,日销售利润为y元,则y=x[480﹣40(x﹣1)]﹣200,其中0<x<13,整理函数y,可得x取何值时,y有最大值,即获得最大利润
【解答】解:设定价在进价的基础上增加x元,日销售利润为y元,则
y=x[480﹣40(x﹣1)]﹣200,
由于x>0,且520﹣40x>0,所以,0<x<13;
即y=﹣40x2+520x﹣200,0<x<13.
所以,当x=﹣=6.5时,y取最大值.
此时售价为6.5+5=11.5
故选:D.
6.【分析】先根据题意,可设一其中一家连锁店销售x辆,则另一家销售(110﹣x)辆,再列出总利润S的表达式,是一个关于x的二次函数,最后求此二次函数的最大值即可.
【解答】解析:依题意,可设一其中一家连锁店销售x辆,则另一家销售(110﹣x)辆,
∴总利润S=﹣5x2+900x﹣16000+300(110﹣x)﹣2000
=﹣5x2+600x+15000(x≥0).
∴当x=60时,S取最大值.
且为Smax=33000.
故选:C.
7.【分析】毛利润等于销售额减去成本,可建立函数关系式,利用导数可求函数的极值点,利用极值就是最值,可得结论.
【解答】解:由题意知:毛利润等于销售额减去成本,即
L(P)=PQ﹣20Q=Q(P﹣20)=(8300﹣170P﹣P2)(P﹣20)
=﹣P3﹣150P2+11700P﹣166000,
所以L′(P)=﹣3P2﹣300P+11700.
令L′(P)=0,解得P=30或P=﹣130(舍去).
此时,L(30)=23000.
因为在P=30附近的左侧L′(P)>0,右侧L′(P)<0.
所以L(30)是极大值,根据实际问题的意义知,L(30)是最大值,
故选:D.
8.【分析】设两段长分别为xcm,(12﹣x)cm,则这两个正三角形面积之和 S=()2+()2,
利用二次函数的性质求出其最小值.
【解答】解:设两段长分别为xcm,(12﹣x)cm,
则这两个正三角形面积之和 S=()2+()2
=(x2﹣12x+72)=[(x﹣6)2+36]≥2,
故选:D.
二、多选题
9.【分析】根据路程和时间关系图,判断甲乙两人的速度,时间关系进行判断即可.
【解答】解:当t=0时,甲乙都在原点,说明甲乙两人是同时出发,故A错误,
甲乙两人最后的最大值相同,则甲乙两人路程一样多,故B正确,
甲到达的时间短,乙到达的时间长,则甲的速度对,乙的速度慢,即甲先到终点,故C错误,D正确,
故选:BD.
10.【分析】根据图象可分析产量的变化情况,前三年增长变慢,后五年停止生产.
【解答】解:在区间[0,3]上,函数图象在任一点处的切线斜率越来越小,表明总产量的增长速度越来越慢,即选项A正确;
由总产量增长越来越慢知,年产量逐年减少,即选项B错误;
在区间[3,8]上,图象呈水平直线,表明总产量保持不变,即年产量为0,因此选项C和D均正确.
故选:ACD.
11.【分析】结合燃油效率情况图依次分析各个选项即可.
【解答】解:对于A,消耗1升汽油,乙车最多可行驶距离大于5千米,故A错误;
对于B,因为当速度相同时,甲的燃油效率最高,所以以相同速度行驶相同路程,三辆车中,甲车消耗汽油最少,故B正确;
对于C,甲车以80千米/小时的速度行驶1小时,此时的燃油效率是10km/L,一共开了80km,所以消耗8升汽油,故C正确;
对于D,当速度小于80千米/小时时,丙车的燃油效率比乙车高,所以相同条件下,在该市用丙车比用乙车省油,故D正确.
故选:BCD.
三、填空题
12.【分析】把点(8,1),(64,4)代入y=alog4x+b,得到关于a,b的方程组,求得a与b的值,可得函数解析式,取y=8,求解对数方程得x值即可.
【解答】解:函数模型为y=alog4x+b,把点(8,1),(64,4)代入,
可得,解得a=2,b=﹣2.
∴y=2log4x﹣2,
由2log4x﹣2=8,得2log4x=10,即log2x=10,得x=210=1024.
∴某业务员要得到8万元奖励,则他的销售额应为1024万元.
故答案为:1024.
13.【分析】增长率问题的一般形式为a(1+x)2=b,a为起始时间的有关数量,b为终止时间的有关数量.本题中a就是2016年的经营收入,b就是2018年的经营收入,从而可求出增长率的值,进而可求2017年预计经营总收入.
【解答】解:2016年的经营总收入为400÷40%=1000(万元).
设年增长率为x(x>0),依题意得,1000(1+x)2=169,
解得:x1=0.3,x2=﹣2.3,
∵x>0
∴x2=﹣2.3不合题意,
∴只取x1=0.3.
1000(1+x)=1000×1.3=130(万元).
即2017年预计经营总收入为130万元.
故答案为:130.
14.【分析】设,把x=0.65,y=0.8代入可得关于k的方程,解出k即可得答案.
【解答】解:因为y与x﹣0.4成反比例,设,
把x=0.65,y=0.8代入得,
解得k=0.2.
所以y与x之间的函数关系式为.
故答案为:.
四、解答题
15.【分析】(1)要使树被圈进去,则ABCD中BC≥a,CD≥4,由此可确定函数的变量的范围.设长BC=x米,宽CD=(16﹣x)米,所以面积y=f(x)=x(16﹣x)=﹣x2+16x;
(2)由(1)得,y=f(x)=﹣x2+16x=﹣(x﹣8)2+64,x∈[a,12],由于对称轴x=8,根据0<a<12,故要进行分类讨论:即8≤a<12;4≤a<8;0<a<4,从而可求y=f(x)的最大值.
【解答】解:(1)要使树被圈进去,则ABCD中BC≥a,CD≥4,
因为篱笆长为16米,所以当长BC=x米时,宽CD=(16﹣x)米.
由于BC≥a,CD≥4,故a≤x≤12,
所以面积y=f(x)=x(16﹣x)=﹣x2+16x,其定义域为x∈[a,12];
(2)由(1)得,y=f(x)=﹣x2+16x=﹣(x﹣8)2+64,x∈[a,12]
对称轴x=8,又因为0<a<12,
所以,当8≤a<12时,x=a时,ymax=﹣a2+16a;
当4≤a<8时,x=8时,ymax=64;
当0<a<4时,x=8时,ymax=64.
16.【分析】(1)令=0,则x=或0(舍0),再利用基本不等式的性质求出x的最大值即可;
(2)原问题等价于存在x>0,使得y=kx﹣(1+k2)x2=3.2成立,即关于x的方程(k2+1)x2﹣20kx+64=0有正根,然后利用韦达定理列出关于k的不等式,解之即可.
【解答】解:(1)令=0,则x=0或,
∵k>0,x>0,
∴x==≤=10,当且仅当=k,即k=1时,等号成立.
故当k=1时,炮的射程最大,为10千米.
(2)炮弹可以击中目标等价于存在x>0,使得y=kx﹣(1+k2)x2=3.2成立,
即关于x的方程(k2+1)x2﹣20kx+64=0有正根,
由韦达定理知,满足两根之和大于0,两根之积大于0,
∴只需Δ=(20k)2﹣4(k2+1)×64≥0,解得k≥或k≤﹣.
∵k>0,∴k≥.
故若炮弹可以击中它,k的取值范围为.
17.【分析】(1)由投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比,结合函数图象,我们可以利用待定系数法来求两种产品的收益与投资的函数关系;
(2)由(1)的结论,我们设投资债券类产品x万元,则股票类投资为20﹣x万元.这时可以构造出一个关于收益y的函数,然后利用求函数最大值的方法进行求解.
【解答】解:(1)f(x)=k1x,,
,,(x≥0),
(x≥0)
(2)设:投资债券类产品x万元,则股票类投资为20﹣x万元.
(0≤x≤20)
令,则==
所以当t=2,即x=16万元时,收益最大,ymax=3万元.
则投资债券等稳健型产品16万元,投资股票等风险型产品4万元获得收益最大,最大收益为3万元.
18.【分析】设污水处理池的长为x米,可得宽为米,列出总造价Q(x)=400(2x+2×)+248×2×+80×200,再根据对勾函数的单调性,即可求出最值.
【解答】解:设污水处理池的长为x米,则宽为米(0<x≤16,0<≤16),
∴12.5≤x≤16.
于是总造价Q(x)=400(2x+2×)+248×2×+80×200.
=800(x+)+16 000,
由对勾函数的性质可知y=x+在(0,18)上单调递减,在(18,+∞)上单调递增,
∴Q(x)在[12.5,16]上是单调递减函数,
∴Q(x)≥Q(16)=45000.
所以当污水处理池的长为16米,宽为12.5米时,总造价最低,最低造价为45 000元.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
