1.3.2-1 基本不等式的概念 课件(共16张PPT)
文档属性
| 名称 | 1.3.2-1 基本不等式的概念 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-23 17:38:26 | ||
图片预览






文档简介
(共16张PPT)
北师大版同步教材精品课件
1.3.2-1 基本不等式的概念
导入新课
上一节课,教材第26页练习第2题,如图.
得到一个不等式:,当时,取“=”.
导入新课
思考讨论:
如图是2002年在北京召开的第24届国际数学家大会的会标,会标是根据中国古代数学家赵爽的弦图设计的,由四个直角三角形拼合而成,正方形的边长为直角三角形的斜边长.
导入新课
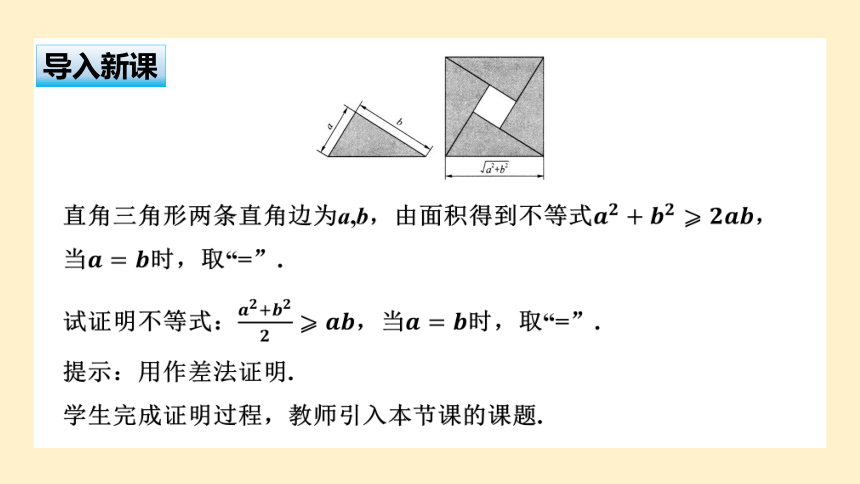
直角三角形两条直角边为a,b,由面积得到不等式,当时,取“=”.
试证明不等式:,当时,取“=”.
提示:用作差法证明.
学生完成证明过程,教师引入本节课的课题.
导入新课
问题1:你能用完整的数学符号语言表述上面的数量关系吗?
(,有,当且仅当时,等号成立)
问题2:该不等关系成立的条件是否可以扩展?在实数集上是否成立?
(在实数集上也成立,即,有,当且仅当时,
等号成立)
设计意图:借助图形得到不等式,给学生以直观感受,然后
通过利用上节学习的作差法证明,提升学生思维的严谨性.
分析结构,获得新知
问题3:,有,当且仅当时,等号成立.
设,取,,能得到什么样的不等式?
(得到,当时,取“=”)
基本不等式:若实数,则,当且仅当时,
等号成立.
其中,称为的算术平均值,称为的几何平均值上述
基本不等式又称为“均值不等式”.
探究新知
问题4:你能用文字语言表述基本不等式吗?
(两个非负实数的算术平均值大于或等于它们的几何平均值)
探究新知
探究新知
注意:
①务必注意基本不等式“”中的字母为非负数,等号成立的条件为.
②与基本不等式有关的各种形式:,,,特别还有,等等.
设计意图:利用不等式,得到,在两个不等式间建立联系,通过分析基本不等式的代数结构特征,得到基本不等式的代数解释,加深对基本不等式的认识.
探究新知
几何解释,直观感知
问题5:我们得到的这个基本不等式有没有几何解释?
阅读教材第27页.
如图,AB是半圆O的直径,点C在AB上,且.
过点C作AB的垂线,交于点D,连接AD,OD,BD.
探究新知
问题6:观察图形并思考:它是如何对基本不等式作出解释的?
(提示:由初中几何知识,得,即)
设计意图:让学生自己寻找基本不等式的几何解释是非常困难的,因此这里给出了几何图形,引导学生将和与图形中的几何元素建立起联系,再观察这些几何元素在变化中表现的大小关系,从而获得基本不等式的几何解释.
探究新知
独立探究,反思深化
阅读教材第28页“思考交流”.
留时间让学生思考、交流、讨论、展示分享.
典例剖析
例1、已知,求证:.
证明
分析
要证,可以先在不等式两边都乘2化为,即 ,利用基本不等式和不等式的基本性质即可证得结论.
因为,所以由基本不等式,得
,当且仅当时,等号成立,
,当且仅当时,等号成立,
,当且仅当时,等号成立.
上面三式相加,得,即,当且仅当时,等号成立.
典例剖析
跟踪训练:
已知,求证:.
证明
因为,所以由基本不等式,得,当且仅当时,等号成立.所以.
设计意图:
例题及跟踪训练题是基本不等式在不等式证明中的简单应用,应熟练掌握.
教材第28页练习第1~4题.
让学生先独立完成,然后相互讨论交流,教师点评后给出答案.
巩固练习
课堂小结
引导学生共同小结:
(1)基本不等式、算术平均值、几何平均值;
(2)教师和学生一起完善知识结构框图,如下图.
设计意图:通过教师和学生一起梳理知识框图,回应教学目标,使学生深刻体会新知识的形成过程,不但梳理了本节的知识,而且优化了学生的认知结构,完善了学生的知识体系.
谢谢您的聆听
Copy paste fonts. Choose the only option to retain text……
Copy paste fonts. Choose the only
option to retain text……
THANKS
北师大版同步教材精品课件
1.3.2-1 基本不等式的概念
导入新课
上一节课,教材第26页练习第2题,如图.
得到一个不等式:,当时,取“=”.
导入新课
思考讨论:
如图是2002年在北京召开的第24届国际数学家大会的会标,会标是根据中国古代数学家赵爽的弦图设计的,由四个直角三角形拼合而成,正方形的边长为直角三角形的斜边长.
导入新课
直角三角形两条直角边为a,b,由面积得到不等式,当时,取“=”.
试证明不等式:,当时,取“=”.
提示:用作差法证明.
学生完成证明过程,教师引入本节课的课题.
导入新课
问题1:你能用完整的数学符号语言表述上面的数量关系吗?
(,有,当且仅当时,等号成立)
问题2:该不等关系成立的条件是否可以扩展?在实数集上是否成立?
(在实数集上也成立,即,有,当且仅当时,
等号成立)
设计意图:借助图形得到不等式,给学生以直观感受,然后
通过利用上节学习的作差法证明,提升学生思维的严谨性.
分析结构,获得新知
问题3:,有,当且仅当时,等号成立.
设,取,,能得到什么样的不等式?
(得到,当时,取“=”)
基本不等式:若实数,则,当且仅当时,
等号成立.
其中,称为的算术平均值,称为的几何平均值上述
基本不等式又称为“均值不等式”.
探究新知
问题4:你能用文字语言表述基本不等式吗?
(两个非负实数的算术平均值大于或等于它们的几何平均值)
探究新知
探究新知
注意:
①务必注意基本不等式“”中的字母为非负数,等号成立的条件为.
②与基本不等式有关的各种形式:,,,特别还有,等等.
设计意图:利用不等式,得到,在两个不等式间建立联系,通过分析基本不等式的代数结构特征,得到基本不等式的代数解释,加深对基本不等式的认识.
探究新知
几何解释,直观感知
问题5:我们得到的这个基本不等式有没有几何解释?
阅读教材第27页.
如图,AB是半圆O的直径,点C在AB上,且.
过点C作AB的垂线,交于点D,连接AD,OD,BD.
探究新知
问题6:观察图形并思考:它是如何对基本不等式作出解释的?
(提示:由初中几何知识,得,即)
设计意图:让学生自己寻找基本不等式的几何解释是非常困难的,因此这里给出了几何图形,引导学生将和与图形中的几何元素建立起联系,再观察这些几何元素在变化中表现的大小关系,从而获得基本不等式的几何解释.
探究新知
独立探究,反思深化
阅读教材第28页“思考交流”.
留时间让学生思考、交流、讨论、展示分享.
典例剖析
例1、已知,求证:.
证明
分析
要证,可以先在不等式两边都乘2化为,即 ,利用基本不等式和不等式的基本性质即可证得结论.
因为,所以由基本不等式,得
,当且仅当时,等号成立,
,当且仅当时,等号成立,
,当且仅当时,等号成立.
上面三式相加,得,即,当且仅当时,等号成立.
典例剖析
跟踪训练:
已知,求证:.
证明
因为,所以由基本不等式,得,当且仅当时,等号成立.所以.
设计意图:
例题及跟踪训练题是基本不等式在不等式证明中的简单应用,应熟练掌握.
教材第28页练习第1~4题.
让学生先独立完成,然后相互讨论交流,教师点评后给出答案.
巩固练习
课堂小结
引导学生共同小结:
(1)基本不等式、算术平均值、几何平均值;
(2)教师和学生一起完善知识结构框图,如下图.
设计意图:通过教师和学生一起梳理知识框图,回应教学目标,使学生深刻体会新知识的形成过程,不但梳理了本节的知识,而且优化了学生的认知结构,完善了学生的知识体系.
谢谢您的聆听
Copy paste fonts. Choose the only option to retain text……
Copy paste fonts. Choose the only
option to retain text……
THANKS
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
