1.4.1 一元二次函数 课件(共17张PPT)
文档属性
| 名称 | 1.4.1 一元二次函数 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-23 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
北师大版同步教材精品课件
1.4.1 一元二次函数
导入新课
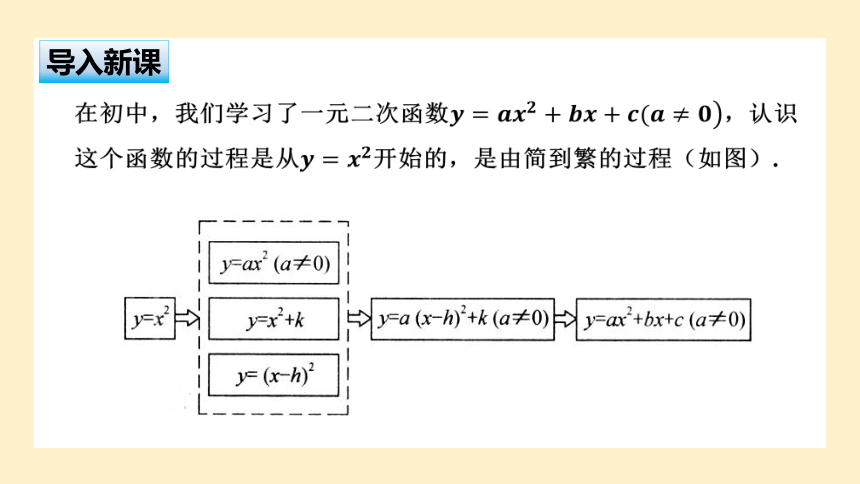
在初中,我们学习了一元二次函数,认识这个函数的过程是从开始的,是由简到繁的过程(如图).
导入新课
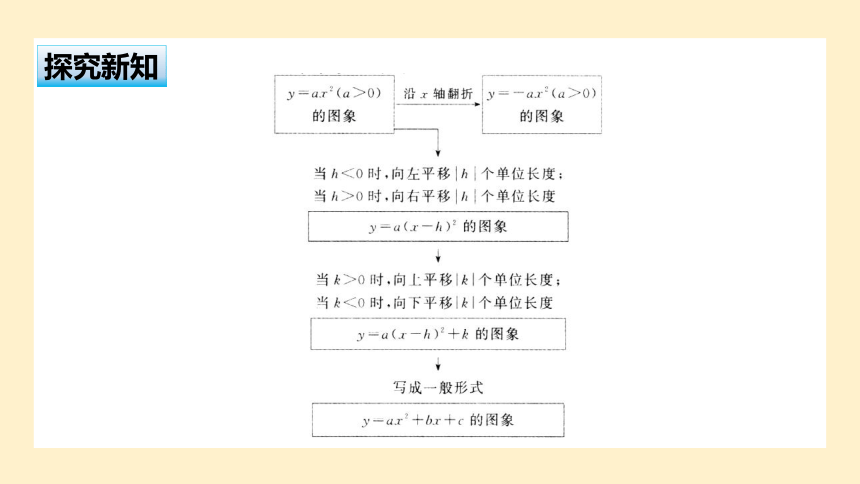
问题1:请分析讨论函数的图象可以由函数的图象经过怎样的变换得到.
设计意图:通过图示让学生初步了解一元二次函数由到的变化过程,提出问题,引发学生思考,引入本节课的课题.
抽象概括,得出规律
教师给学生留时间让学生思考、交流、讨论,然后共同得出结论:
一元二次函数都可以通过配方化为
,若设,
则有.
函数的图象,可以由函数的图象
平移而得到.
探究新知
探究新知
探究新知
问题2:你能说出一元二次函数的性质吗?
教师引导学生从函数图象的对称轴,函数的单调性、最值等方面分析:
(1)函数的图象是一条抛物线,顶点坐标
是,对称轴是直线.
(2)当时,抛物线开口向上;在区间上,函数值y随自变量x的增大而减小;在区间上,函数值y随自变量x的增大而增大;函数在处有最小值,记作.
探究新知
当时,抛物线开口向下;在区间上,函数值y随自变量x的增大而增大;在区间上,函数值y随自变量x的增大而减小;函数在处有最大值,记作.
设计意图:通过配方把一元二次函数的一般式配成顶点式.通过研究一元二次函数的图象是如何由函数的图象经过平移变换得到的,让学生体会函数图象与函数解析式之间的内在联系通过一元二次函数的顶点式再次认识一元二次函数的性质.
典例剖析
例1、已知一元二次函数.
(1)指出它的图象可以由函数的图象经过怎样的变换而得到;
(2)指出它的图象的对称轴,试述函数值的变化趋势及函数的最大值或最小值.
问题3:要想得到函数的图象与函数的图象之间的关系,我们要对函数的解析式进行怎样处理?
典例剖析
学生思考后回答;要对函数的解析式进行配方.
配方,得
.
典例剖析
追问1:你能说出由函数的图象经过怎样的变换可得到函数
的图象吗?
找学生回答:函数的图象可以由函数的图象向左平移2个单位长度,再向上平移3个单位长度而得到.
追问2:根据(1),你能描述函数值的变化趋势及函数的最大值或最
小值吗?
由(1)可知:该函数的图象开口向上,对称轴为直线;
在区间上,函数值y随自变量x的增大而减小,在区间
上,函数值y随自变量x的增大而增大;函数在处取得最小值3,即.
典例剖析
跟踪训练:
1.画出一元二次函数,的图象,考虑它们的开口方向对称轴和顶点坐标.
解析
如图所示.
抛物线的开口向下,对称轴是直线,顶点坐标是;抛物线的开口向下,对称轴是直线,顶点坐标是.
典例剖析
2.画出函数的图象,指出它的开口方向、对称轴及顶点坐标.抛物线经过怎样的变换可以得到抛物线
?
解析
如图所示.
典例剖析
解析
函数的图象开口向下,对称轴是直线,顶点坐标是.
把抛物线向下平移1个单位长度,再向左平移1个单位长度,就得到抛物线.
典例剖析
设计意图:通过例题与跟踪训练加深学生对图象变换的理解与认识,以及对一元二次函数的图象与性质的理解与认识.因为一元二次函数的图象是抛物线,是轴对称图形,所以作图时常用简化的描点法,其步骤是:(1)先找出顶点坐标,画出对称轴;(2)找出抛物线上关于对称轴对称的四个点(如与坐标轴的交点等);(3)把上述五个点按从左到右的顺序用平滑曲线连接起来.
1.用配方法求出下列函数图象的对称轴及函数的最大值或最小值:
(1);(2).
2.已知一元二次函数.
(1)指出它的图象可以由函数的图象经过怎样的变换而得到;
(2)指出它的图象的对称轴,试述函数值的变化趋势及最大值或最小值.
让学生先独立完成,然后相互讨论交流,教师点评后给出答案.
巩固练习
课堂小结
引导学生共同小结:
1.一元二次函数的一般式和顶点式中,各参数对函数图象的影响.
2.从函数的图象到函数的图象的变化过程.
3.一元二次函数的性质.
谢谢您的聆听
Copy paste fonts. Choose the only option to retain text……
Copy paste fonts. Choose the only
option to retain text……
THANKS
北师大版同步教材精品课件
1.4.1 一元二次函数
导入新课
在初中,我们学习了一元二次函数,认识这个函数的过程是从开始的,是由简到繁的过程(如图).
导入新课
问题1:请分析讨论函数的图象可以由函数的图象经过怎样的变换得到.
设计意图:通过图示让学生初步了解一元二次函数由到的变化过程,提出问题,引发学生思考,引入本节课的课题.
抽象概括,得出规律
教师给学生留时间让学生思考、交流、讨论,然后共同得出结论:
一元二次函数都可以通过配方化为
,若设,
则有.
函数的图象,可以由函数的图象
平移而得到.
探究新知
探究新知
探究新知
问题2:你能说出一元二次函数的性质吗?
教师引导学生从函数图象的对称轴,函数的单调性、最值等方面分析:
(1)函数的图象是一条抛物线,顶点坐标
是,对称轴是直线.
(2)当时,抛物线开口向上;在区间上,函数值y随自变量x的增大而减小;在区间上,函数值y随自变量x的增大而增大;函数在处有最小值,记作.
探究新知
当时,抛物线开口向下;在区间上,函数值y随自变量x的增大而增大;在区间上,函数值y随自变量x的增大而减小;函数在处有最大值,记作.
设计意图:通过配方把一元二次函数的一般式配成顶点式.通过研究一元二次函数的图象是如何由函数的图象经过平移变换得到的,让学生体会函数图象与函数解析式之间的内在联系通过一元二次函数的顶点式再次认识一元二次函数的性质.
典例剖析
例1、已知一元二次函数.
(1)指出它的图象可以由函数的图象经过怎样的变换而得到;
(2)指出它的图象的对称轴,试述函数值的变化趋势及函数的最大值或最小值.
问题3:要想得到函数的图象与函数的图象之间的关系,我们要对函数的解析式进行怎样处理?
典例剖析
学生思考后回答;要对函数的解析式进行配方.
配方,得
.
典例剖析
追问1:你能说出由函数的图象经过怎样的变换可得到函数
的图象吗?
找学生回答:函数的图象可以由函数的图象向左平移2个单位长度,再向上平移3个单位长度而得到.
追问2:根据(1),你能描述函数值的变化趋势及函数的最大值或最
小值吗?
由(1)可知:该函数的图象开口向上,对称轴为直线;
在区间上,函数值y随自变量x的增大而减小,在区间
上,函数值y随自变量x的增大而增大;函数在处取得最小值3,即.
典例剖析
跟踪训练:
1.画出一元二次函数,的图象,考虑它们的开口方向对称轴和顶点坐标.
解析
如图所示.
抛物线的开口向下,对称轴是直线,顶点坐标是;抛物线的开口向下,对称轴是直线,顶点坐标是.
典例剖析
2.画出函数的图象,指出它的开口方向、对称轴及顶点坐标.抛物线经过怎样的变换可以得到抛物线
?
解析
如图所示.
典例剖析
解析
函数的图象开口向下,对称轴是直线,顶点坐标是.
把抛物线向下平移1个单位长度,再向左平移1个单位长度,就得到抛物线.
典例剖析
设计意图:通过例题与跟踪训练加深学生对图象变换的理解与认识,以及对一元二次函数的图象与性质的理解与认识.因为一元二次函数的图象是抛物线,是轴对称图形,所以作图时常用简化的描点法,其步骤是:(1)先找出顶点坐标,画出对称轴;(2)找出抛物线上关于对称轴对称的四个点(如与坐标轴的交点等);(3)把上述五个点按从左到右的顺序用平滑曲线连接起来.
1.用配方法求出下列函数图象的对称轴及函数的最大值或最小值:
(1);(2).
2.已知一元二次函数.
(1)指出它的图象可以由函数的图象经过怎样的变换而得到;
(2)指出它的图象的对称轴,试述函数值的变化趋势及最大值或最小值.
让学生先独立完成,然后相互讨论交流,教师点评后给出答案.
巩固练习
课堂小结
引导学生共同小结:
1.一元二次函数的一般式和顶点式中,各参数对函数图象的影响.
2.从函数的图象到函数的图象的变化过程.
3.一元二次函数的性质.
谢谢您的聆听
Copy paste fonts. Choose the only option to retain text……
Copy paste fonts. Choose the only
option to retain text……
THANKS
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
