数学人教A版(2019)必修第一册5.1.2弧度制 课件(共33张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册5.1.2弧度制 课件(共33张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-23 20:03:33 | ||
图片预览










文档简介
(共33张PPT)
人教A版2019必修第一册
第 5章 三角函数
5.1.2弧度制
目 录
1 学习目标
2 新课讲解
3 课本例题
4 课本练习
5 题型分类讲解
6 随堂检测
7 课后作业
学习目标
1.了解弧度制下,角的集合与实数集之间的一一对应关系.
2.理解“弧度的角”的定义,掌握弧度与角度的换算、弧长公式和扇形面积公式,熟悉特殊角的弧度数.(重点、难点)
3.了解“角度制”与“弧度制”的区别与联系.(易错点)
情境导入
炎炎夏日,用纸扇驱走闷热,无疑是一种好办法.扇子在美观设计上,可考虑用料、图案和形状.若从数学角度看,我们能否用黄金比例(0.618)去设计一把富有美感的纸扇?要探索这个问题首先要认识一种新的角度单位——弧度.
【探究1】 在平面几何里,度量角的大小用什么单位?
【提示】角度制的单位有:度、分、秒。
【探究2】1°的角是如何定义的?
【提示】规定:圆周的圆心角称作1°角。
这种用度做单位来度量角的制度叫做角度制 .
【探究3】日常生活中,度量长度可用不同的单位,如:一张课桌长80厘米,也可以说长0.8米,显然两种结果出现了不同的数值,那么有没有一种更好的方法去表示角呢?
【提示】在数学和其他科学研究中还经常用到另一种度量角的制度 — 弧度制。
【探究4】在圆内,圆心角的大小和半径大小有关系吗?
【提示】无关
【探究5】角度为、的圆心角,半径r=1,2,3时,
(1)分别计算相对应的弧长l
(2)分别计算对应弧长与半径之比
通过上面的计算,你发现了什么规律?
【提示】①.圆心角不变,比值不变;比值的大小与所取的圆的半径大小无关;
②圆心角改变,比值改变;比值的大小只与圆心角的大小有关.
下面介绍在数学和其他科学研究中经常采用的另一种度量角的单位制——弧度制.
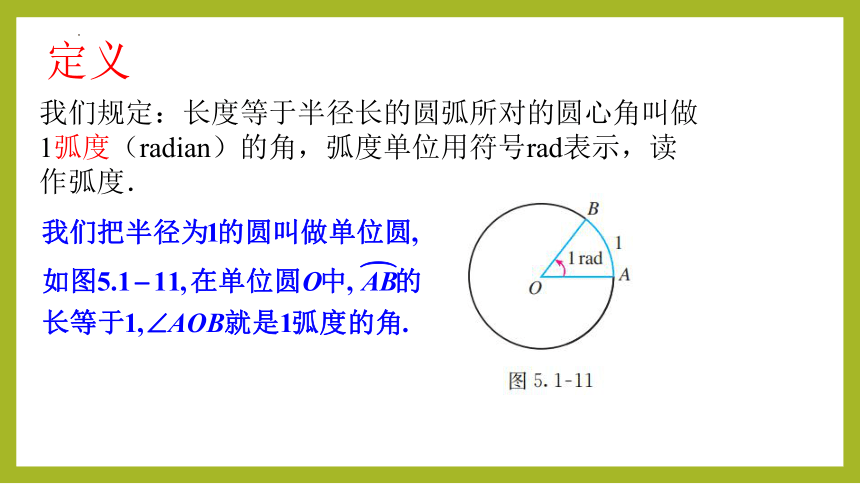
我们规定:长度等于半径长的圆弧所对的圆心角叫做1弧度(radian)的角,弧度单位用符号rad表示,读作弧度.
定义
一般地,正角的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度数是0.
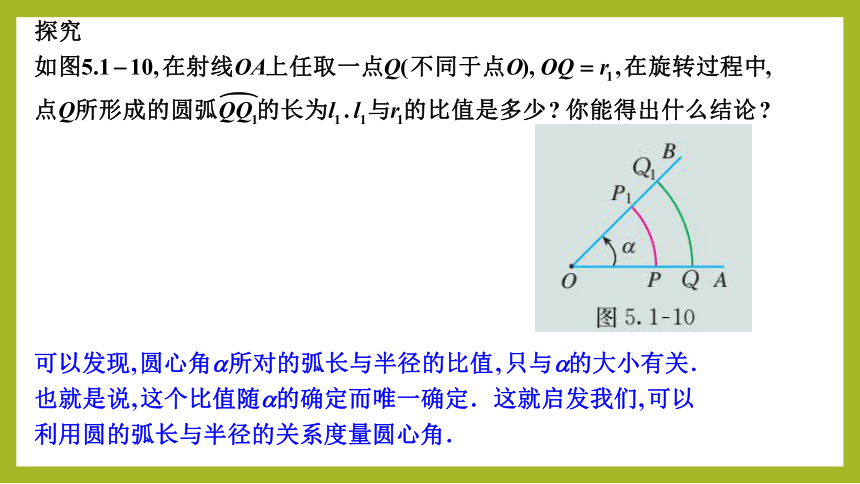
探究
角度制、弧度制都是角的度量制,它们之间应该可以换算.如何换算呢?
角度与弧度的互化
例4.按照下列要求,把化成弧度:
(1)精确值;(2)精确到0.001的近似值.
解:(1)因为所以
(2)利用计算器可得:
1.角度制与弧度制的互化
例5.将3.14 换算成角度(用度数表示,精确到0.001).
解:利用计算器可得:
今后用弧度制表示角时,“弧度”二字或者“”通常省略不写,而只写该角所对应的弧度数.例如,角就表示是2的角; 就表示 的角的正弦,即.
填写下列特殊角的度数与弧度数的对应表:
度 0° 30° 45° 60° 90° 120° 135° 150° 180° 270° 360°
弧度 0 2
角的概念推广后,在弧度制下,角的集合与实数集之间建立起一一对应的关系:每一个角都有唯一的一个实数(等于这个角的弧度数)与它对应;反过来,每一个实数也都有唯一的一个角(即弧度数等于这个实数的角)与它对应.
正角
零角
负角
正实数
0
负实数
例6.利用弧度制证明下列关于扇形的公式:
(1)(2)(3)
其中是圆的半径,为圆心角,是扇形的弧长,是扇形的面积.
证明:由公式可得:.下面证明(2)(3).
半径为,圆心角为的扇形的弧长公式和面积公式分别是:
将转换为弧度制,得:,于是,.
将代入上式,即得
显然,弧度制下的弧长公式和扇形面积公式形式简单了.在今后的学习中,我们还将进一步看到弧度制带来的便利.
2.扇形的弧长与面积问题
扇形的弧长和面积公式:
设扇形的半径为弧长为为其圆心角,则:
弧长公式
扇形面积公式
课本练习
3、用弧度表示:
(1)终边在x轴的角的集合 (2)终边在y轴的角的集合
4.利用计算工具比较下列各对值的大小:
(1)cos0.75°和cos0.75; (2)tan1.2°和tan1.2.
5..分别用角度制,弧度制下的弧长公式计算半径为1cm的圆中,60°的圆心角对对弧的长度。
6.已知半径为120mm的圆上,有一条弧长为144mm,求该弧所对圆心的弧度数和角度数。
【例1】把下列角度化成弧度或弧度化成角度.
(1)72°;(2)-300°;(3)2;(4).
解:(1)
(2)
(3)
(4)
题型一:角度与弧度的换算
题型分类讲解
【变式】把下列角度与弧度进行互化.
(1)110°;(2)-32°;(3);(4);(5)112°30
解:(1)
(2)
(3)
(4)
(5)112°30
【例2】已知角
(1)将改写成的形式,并指出是第几象限角;
(2)在内找出与终边相同的角.
解:(1)∵
又∴角与终边相同,是第三象限的角.
(2)∵与终边相同的角为由知∴在内与终边相同的角是
题型二:用弧度制表示角有关的角
【变式】用弧度制表示终边在图中阴影区域内角的集合(包括边界),并判断2012°是不是这个集合的元素.
解:因为150°
所以终边在阴影区域内角的集合为
.
因为2012°=212°+5
又
所以2012°
【例3】.已知扇形的周长为10,面积为,求扇形圆心角的弧度数.
解:设扇形圆心角的弧度数为,弧长为半径为,据题意有:解得,
当时,此时,舍去.
当时,此时,.
综上所述,扇形圆心角的弧度数为.
题型三:扇形的弧长与面积公式
【变式】已知一扇形的圆心角是72°,半径为20,求扇形的面积.
解:设扇形的弧长为
∵圆心角72°
∴扇形弧长
于是,扇形的面积
随堂检测
弧度制 角度制
度量单位 弧度(10进制) 度(60进制,1 =60,1′=60 )
单位规定 把长度等于半径长的弧所对的圆心角叫做1弧度的角。 周角的1/360叫做1度的角。
换算关系
基本关系
导出关系
课堂小结
人教A版2019必修第一册
第 5章 三角函数
5.1.2弧度制
目 录
1 学习目标
2 新课讲解
3 课本例题
4 课本练习
5 题型分类讲解
6 随堂检测
7 课后作业
学习目标
1.了解弧度制下,角的集合与实数集之间的一一对应关系.
2.理解“弧度的角”的定义,掌握弧度与角度的换算、弧长公式和扇形面积公式,熟悉特殊角的弧度数.(重点、难点)
3.了解“角度制”与“弧度制”的区别与联系.(易错点)
情境导入
炎炎夏日,用纸扇驱走闷热,无疑是一种好办法.扇子在美观设计上,可考虑用料、图案和形状.若从数学角度看,我们能否用黄金比例(0.618)去设计一把富有美感的纸扇?要探索这个问题首先要认识一种新的角度单位——弧度.
【探究1】 在平面几何里,度量角的大小用什么单位?
【提示】角度制的单位有:度、分、秒。
【探究2】1°的角是如何定义的?
【提示】规定:圆周的圆心角称作1°角。
这种用度做单位来度量角的制度叫做角度制 .
【探究3】日常生活中,度量长度可用不同的单位,如:一张课桌长80厘米,也可以说长0.8米,显然两种结果出现了不同的数值,那么有没有一种更好的方法去表示角呢?
【提示】在数学和其他科学研究中还经常用到另一种度量角的制度 — 弧度制。
【探究4】在圆内,圆心角的大小和半径大小有关系吗?
【提示】无关
【探究5】角度为、的圆心角,半径r=1,2,3时,
(1)分别计算相对应的弧长l
(2)分别计算对应弧长与半径之比
通过上面的计算,你发现了什么规律?
【提示】①.圆心角不变,比值不变;比值的大小与所取的圆的半径大小无关;
②圆心角改变,比值改变;比值的大小只与圆心角的大小有关.
下面介绍在数学和其他科学研究中经常采用的另一种度量角的单位制——弧度制.
我们规定:长度等于半径长的圆弧所对的圆心角叫做1弧度(radian)的角,弧度单位用符号rad表示,读作弧度.
定义
一般地,正角的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度数是0.
探究
角度制、弧度制都是角的度量制,它们之间应该可以换算.如何换算呢?
角度与弧度的互化
例4.按照下列要求,把化成弧度:
(1)精确值;(2)精确到0.001的近似值.
解:(1)因为所以
(2)利用计算器可得:
1.角度制与弧度制的互化
例5.将3.14 换算成角度(用度数表示,精确到0.001).
解:利用计算器可得:
今后用弧度制表示角时,“弧度”二字或者“”通常省略不写,而只写该角所对应的弧度数.例如,角就表示是2的角; 就表示 的角的正弦,即.
填写下列特殊角的度数与弧度数的对应表:
度 0° 30° 45° 60° 90° 120° 135° 150° 180° 270° 360°
弧度 0 2
角的概念推广后,在弧度制下,角的集合与实数集之间建立起一一对应的关系:每一个角都有唯一的一个实数(等于这个角的弧度数)与它对应;反过来,每一个实数也都有唯一的一个角(即弧度数等于这个实数的角)与它对应.
正角
零角
负角
正实数
0
负实数
例6.利用弧度制证明下列关于扇形的公式:
(1)(2)(3)
其中是圆的半径,为圆心角,是扇形的弧长,是扇形的面积.
证明:由公式可得:.下面证明(2)(3).
半径为,圆心角为的扇形的弧长公式和面积公式分别是:
将转换为弧度制,得:,于是,.
将代入上式,即得
显然,弧度制下的弧长公式和扇形面积公式形式简单了.在今后的学习中,我们还将进一步看到弧度制带来的便利.
2.扇形的弧长与面积问题
扇形的弧长和面积公式:
设扇形的半径为弧长为为其圆心角,则:
弧长公式
扇形面积公式
课本练习
3、用弧度表示:
(1)终边在x轴的角的集合 (2)终边在y轴的角的集合
4.利用计算工具比较下列各对值的大小:
(1)cos0.75°和cos0.75; (2)tan1.2°和tan1.2.
5..分别用角度制,弧度制下的弧长公式计算半径为1cm的圆中,60°的圆心角对对弧的长度。
6.已知半径为120mm的圆上,有一条弧长为144mm,求该弧所对圆心的弧度数和角度数。
【例1】把下列角度化成弧度或弧度化成角度.
(1)72°;(2)-300°;(3)2;(4).
解:(1)
(2)
(3)
(4)
题型一:角度与弧度的换算
题型分类讲解
【变式】把下列角度与弧度进行互化.
(1)110°;(2)-32°;(3);(4);(5)112°30
解:(1)
(2)
(3)
(4)
(5)112°30
【例2】已知角
(1)将改写成的形式,并指出是第几象限角;
(2)在内找出与终边相同的角.
解:(1)∵
又∴角与终边相同,是第三象限的角.
(2)∵与终边相同的角为由知∴在内与终边相同的角是
题型二:用弧度制表示角有关的角
【变式】用弧度制表示终边在图中阴影区域内角的集合(包括边界),并判断2012°是不是这个集合的元素.
解:因为150°
所以终边在阴影区域内角的集合为
.
因为2012°=212°+5
又
所以2012°
【例3】.已知扇形的周长为10,面积为,求扇形圆心角的弧度数.
解:设扇形圆心角的弧度数为,弧长为半径为,据题意有:解得,
当时,此时,舍去.
当时,此时,.
综上所述,扇形圆心角的弧度数为.
题型三:扇形的弧长与面积公式
【变式】已知一扇形的圆心角是72°,半径为20,求扇形的面积.
解:设扇形的弧长为
∵圆心角72°
∴扇形弧长
于是,扇形的面积
随堂检测
弧度制 角度制
度量单位 弧度(10进制) 度(60进制,1 =60,1′=60 )
单位规定 把长度等于半径长的弧所对的圆心角叫做1弧度的角。 周角的1/360叫做1度的角。
换算关系
基本关系
导出关系
课堂小结
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
