2.4.2 简单幂函数的图象和性质 课件(共16张PPT)
文档属性
| 名称 | 2.4.2 简单幂函数的图象和性质 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-23 21:02:44 | ||
图片预览






文档简介
(共16张PPT)
2.4.2
简单幂函数的图象和性质
北师大版同步教材精品课件
初中学习了函数、反比例函数、二次函数等,
对它们的图象和性质已经很熟悉了
后面将学习“”可以记作“”、“”可以记作“”
以上都是形如“”的函数,在实际生活中经常会遇到
导入新课
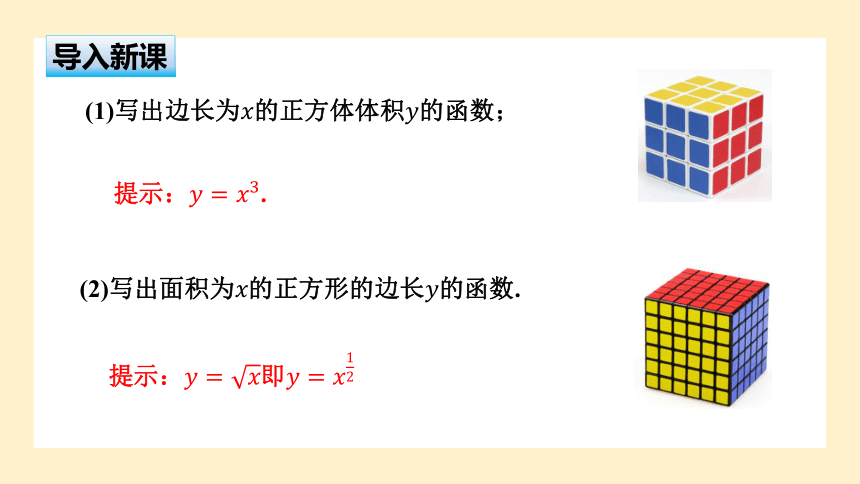
(1)写出边长为的正方体体积的函数;
提示:.
(2)写出面积为的正方形的边长的函数.
提示:即
导入新课
一般地,形如(为常数)的函数,称为幂函数.
如:函数、等等
探究新知
①幂函数的指数是常数,底数是自变量,且指数式前面的系数是1;
②幂函数的图象和性质,根据不同的指数,视其情况具体分析,一般从函数的定义域、奇偶性、单调性、经过的特殊点等方面入手,分析画出其图象.
探究新知
(1)将函数的图象画在同一个坐标系中,并完成下表:
探究新知
(1)将函数的图象画在同一个坐标系中
可以看出:
幂函数图象
过定点(1,1)
探究新知
(2)下列各图,只画出了函数在轴一侧的图象,请画出轴另一侧的图象,并说出画法的依据.
前三个函数为奇函数,所以图象关于原点中心对称,
后两个函数为偶函数,图象关于轴对称.
探究新知
(1)若幂函数在上为减函数,求实数的值;
(2)已知函数、、在第一象限
的函数图象如图,试比较的大小;
(3)试利用函数的性质,比较的大小:
.
(4)已知幂函数的图象关于轴对称,且在上为减函数,解关于的不等式.
巩固练习
(1)若幂函数在上为减函数,求实数的值;
函数为幂函数,则,得或,
函数为或,又函数在上为减函数,
所以.
巩固练习
解析
(2)已知函数、、在第一象限的函数图象如图,试比较的大小;
由的图象,函数单减,则,再取特殊值,则,则所以.
巩固练习
解析
(3)试利用函数的性质,比较的大小:
.
由幂函数,即的性质,,即
再由幂函数的图象,可得,
即
所以.
巩固练习
解析
(4)已知幂函数的图象关于轴对称,且在上为减函数,解关于的不等式.
函数在上为减函数,
则,即,,故或.
又图象关于轴对称,函数为偶函数,则为偶数,所以
不等式即为,再由幂函数的图象
得或或
所以不等式的解集为.
巩固练习
解析
①幂函数的图象和性质,因不同的指数,差异是比较大的,一般通过分析函数的定义域、奇偶性、单调性和经过的特殊点等等得出图象和性质;
②在区间上,幂函数的图象均过定点,当时,幂函数单调递增,当时,单调递减,当时,幂函数为
,即;
③特殊值法在幂函数问题中常常用到,这样可以省去很多不必要的分析过程.
总结归纳
1.教材P66,练习3.
课后作业
2.教材P67,习题2—4:B 组第1题
谢谢您的聆听
Copy paste fonts. Choose the only option to retain text……
Copy paste fonts. Choose the only
option to retain text……
THANKS
2.4.2
简单幂函数的图象和性质
北师大版同步教材精品课件
初中学习了函数、反比例函数、二次函数等,
对它们的图象和性质已经很熟悉了
后面将学习“”可以记作“”、“”可以记作“”
以上都是形如“”的函数,在实际生活中经常会遇到
导入新课
(1)写出边长为的正方体体积的函数;
提示:.
(2)写出面积为的正方形的边长的函数.
提示:即
导入新课
一般地,形如(为常数)的函数,称为幂函数.
如:函数、等等
探究新知
①幂函数的指数是常数,底数是自变量,且指数式前面的系数是1;
②幂函数的图象和性质,根据不同的指数,视其情况具体分析,一般从函数的定义域、奇偶性、单调性、经过的特殊点等方面入手,分析画出其图象.
探究新知
(1)将函数的图象画在同一个坐标系中,并完成下表:
探究新知
(1)将函数的图象画在同一个坐标系中
可以看出:
幂函数图象
过定点(1,1)
探究新知
(2)下列各图,只画出了函数在轴一侧的图象,请画出轴另一侧的图象,并说出画法的依据.
前三个函数为奇函数,所以图象关于原点中心对称,
后两个函数为偶函数,图象关于轴对称.
探究新知
(1)若幂函数在上为减函数,求实数的值;
(2)已知函数、、在第一象限
的函数图象如图,试比较的大小;
(3)试利用函数的性质,比较的大小:
.
(4)已知幂函数的图象关于轴对称,且在上为减函数,解关于的不等式.
巩固练习
(1)若幂函数在上为减函数,求实数的值;
函数为幂函数,则,得或,
函数为或,又函数在上为减函数,
所以.
巩固练习
解析
(2)已知函数、、在第一象限的函数图象如图,试比较的大小;
由的图象,函数单减,则,再取特殊值,则,则所以.
巩固练习
解析
(3)试利用函数的性质,比较的大小:
.
由幂函数,即的性质,,即
再由幂函数的图象,可得,
即
所以.
巩固练习
解析
(4)已知幂函数的图象关于轴对称,且在上为减函数,解关于的不等式.
函数在上为减函数,
则,即,,故或.
又图象关于轴对称,函数为偶函数,则为偶数,所以
不等式即为,再由幂函数的图象
得或或
所以不等式的解集为.
巩固练习
解析
①幂函数的图象和性质,因不同的指数,差异是比较大的,一般通过分析函数的定义域、奇偶性、单调性和经过的特殊点等等得出图象和性质;
②在区间上,幂函数的图象均过定点,当时,幂函数单调递增,当时,单调递减,当时,幂函数为
,即;
③特殊值法在幂函数问题中常常用到,这样可以省去很多不必要的分析过程.
总结归纳
1.教材P66,练习3.
课后作业
2.教材P67,习题2—4:B 组第1题
谢谢您的聆听
Copy paste fonts. Choose the only option to retain text……
Copy paste fonts. Choose the only
option to retain text……
THANKS
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
