数学人教A版(2019)选择性必修第一册2.4.1圆的标准方程 课件(共17张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.4.1圆的标准方程 课件(共17张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 953.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-23 21:08:57 | ||
图片预览





文档简介
(共17张PPT)
2.4 圆的方程
课前导读:
多边形和圆是平面几何中的两类基本图形.建立直线的方程后,
我们可以运用它研究多边形这些“直线形”,解决边所在直线的平行或垂直、边与边的交点以及点到线段所在直线的距离等问题.类似地,为了研究圆的有关性质,解决与圆有关的问题,我们首先需要建立圆的方程.
我国的墨子:圆,一中同长也.
意思:圆有一个圆心,圆心到圆周上各点的距离(即半径)都相等.
2.4.1 圆的标准方程
学习目标:
1.理解圆的标准方程的推导过程,体会类比的方法和数形结合思想;
2.会判断点与圆的位置关系;
3.会根据给定条件求圆的标准方程,体会数形结合以及方程思想.
重点:
圆的标准方程的推导及求法
难点:
圆的标准方程的求法
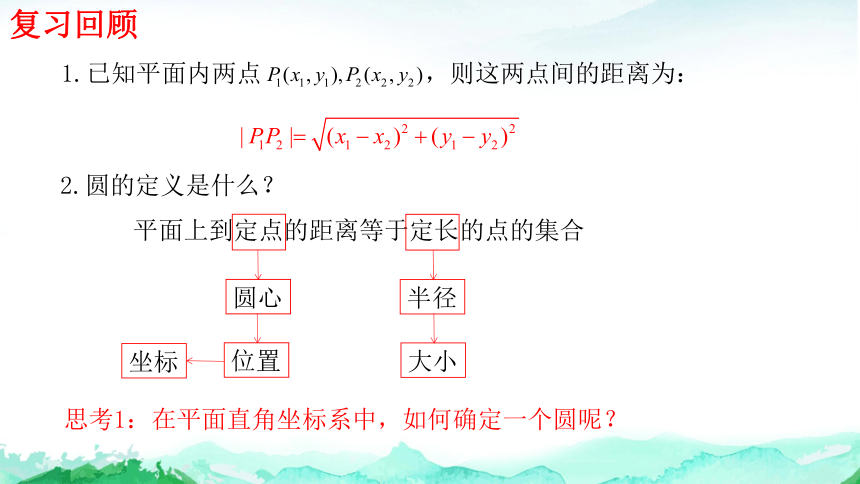
复习回顾
1.已知平面内两点 ,则这两点间的距离为:
2.圆的定义是什么?
平面上到定点的距离等于定长的点的集合
圆心
半径
位置
大小
思考1:在平面直角坐标系中,如何确定一个圆呢?
坐标
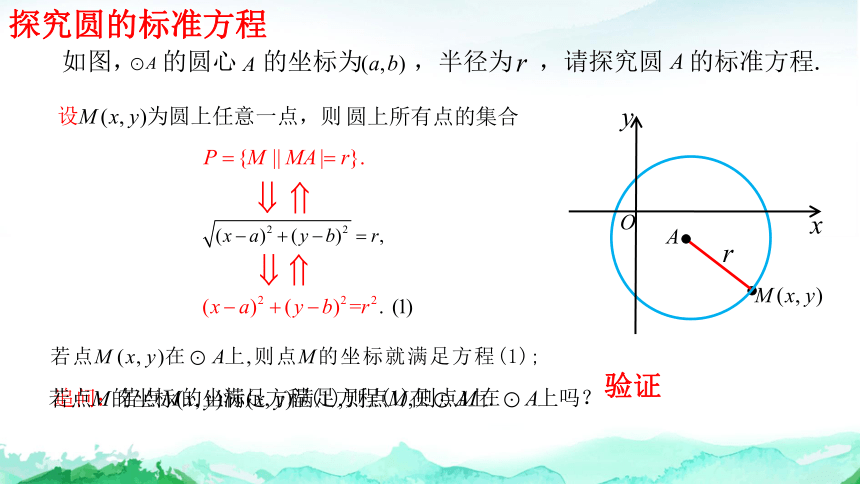
探究圆的标准方程
验证
如图, 的圆心 的坐标为 ,半径为 ,请探究圆 的标准方程.
圆的标准方程
圆心为 ,半径为 的圆的标准方程为:
学以致用:
判断下列方程是不是圆的方程?若是,请说出圆心坐标和半径.
方程的结构特征:
①关于 的 元 次方程,共含有 个参数;
②括号内 的系数都是 ;括号外连接符号为 .
二
二
三
1
+
×
√
?
典例剖析
例1 写出圆心为 ,半径长等于 的圆的标准方程,并判断点 ,
是否在这个圆上.
思考2:如何判断一个点是否在一个圆上呢?
典例剖析
例1 写出圆心为 ,半径长等于 的圆的方程,并判断点 ,
是否在这个圆上.
A
x
y
O
M2
M1
点与圆的位置关系
交流合作
例2 的三个顶点分别是 求 的外接圆的标准方程.
因为 三点都在圆上,所以它们的坐标都满足方程①.
解:设所求的方程是
①
于是
小组合作任务:
1.如何求解上述方程组?
2.动手画一画:在学案例2给定的图形中,作出 的外接圆的圆心,并画出该圆.是否发现求解本题的新的方法?
交流合作
例2 的三个顶点分别是 求 的外接圆的标准方程.
因为 三点都在圆上,所以它们的坐标都满足方程①.
解:设所求的方程是
①
于是
即
②
③
④
消去 ,得
解此方程组,得
代入②式,得
待定系数法
交流合作
例2 的三个顶点分别是 求 的外接圆的标准方程.
1.圆心:两条弦的垂直平分线的交点
2.半径:圆心与圆上一点的距离
几何法:
小组合作任务:
1.如何求解上述方程组?
2.动手画一画:在学案例2给定的图形中,作出 的外接圆的圆心,并画出该圆.是否发现求解本题的新的方法?
(1)几何法
它是利用图形的几何性质,如圆的性质等,直接求出圆的圆心和半径,
代入圆的标准方程,从而得到圆的标准方程.
(2)待定系数法
由三个独立条件得到三个方程,解方程组以得到圆的标准方程中三个参数,从而确定圆的标准方程.它是求圆的方程最常用的方法,一般步骤是:
①设——设所求圆的方程为(x-a)2+(y-b)2=r2;
②列——由已知条件,建立关于a,b,r的方程组;
③解——解方程组,求出a,b,r;
④代——将a,b,r代入所设方程,得所求圆的方程.
求圆的标准方程的方法
争分夺秒
例3 已知圆心为 的圆经过 两点,且圆心 在直线
上,求此圆的标准方程.
方法一:几何法
方法二:待定系数法
解:设所求的方程是
①
规则:1.只需给出方法和思路,不求结果;
2.每种方法和思路,最先回答正确者获胜!
课堂小结
当堂检测
B
C
1.必做题:课本88页第3题;
2.选做题:课本88页第5题;
3.延伸写作:
查阅资料,形成“阿波罗尼斯圆”有关的小文章,并通过课本89页第9题进行验证!
作业布置
希望本节课的学习,能为你以后的数学学习起到推波助澜的作用!
2.4 圆的方程
课前导读:
多边形和圆是平面几何中的两类基本图形.建立直线的方程后,
我们可以运用它研究多边形这些“直线形”,解决边所在直线的平行或垂直、边与边的交点以及点到线段所在直线的距离等问题.类似地,为了研究圆的有关性质,解决与圆有关的问题,我们首先需要建立圆的方程.
我国的墨子:圆,一中同长也.
意思:圆有一个圆心,圆心到圆周上各点的距离(即半径)都相等.
2.4.1 圆的标准方程
学习目标:
1.理解圆的标准方程的推导过程,体会类比的方法和数形结合思想;
2.会判断点与圆的位置关系;
3.会根据给定条件求圆的标准方程,体会数形结合以及方程思想.
重点:
圆的标准方程的推导及求法
难点:
圆的标准方程的求法
复习回顾
1.已知平面内两点 ,则这两点间的距离为:
2.圆的定义是什么?
平面上到定点的距离等于定长的点的集合
圆心
半径
位置
大小
思考1:在平面直角坐标系中,如何确定一个圆呢?
坐标
探究圆的标准方程
验证
如图, 的圆心 的坐标为 ,半径为 ,请探究圆 的标准方程.
圆的标准方程
圆心为 ,半径为 的圆的标准方程为:
学以致用:
判断下列方程是不是圆的方程?若是,请说出圆心坐标和半径.
方程的结构特征:
①关于 的 元 次方程,共含有 个参数;
②括号内 的系数都是 ;括号外连接符号为 .
二
二
三
1
+
×
√
?
典例剖析
例1 写出圆心为 ,半径长等于 的圆的标准方程,并判断点 ,
是否在这个圆上.
思考2:如何判断一个点是否在一个圆上呢?
典例剖析
例1 写出圆心为 ,半径长等于 的圆的方程,并判断点 ,
是否在这个圆上.
A
x
y
O
M2
M1
点与圆的位置关系
交流合作
例2 的三个顶点分别是 求 的外接圆的标准方程.
因为 三点都在圆上,所以它们的坐标都满足方程①.
解:设所求的方程是
①
于是
小组合作任务:
1.如何求解上述方程组?
2.动手画一画:在学案例2给定的图形中,作出 的外接圆的圆心,并画出该圆.是否发现求解本题的新的方法?
交流合作
例2 的三个顶点分别是 求 的外接圆的标准方程.
因为 三点都在圆上,所以它们的坐标都满足方程①.
解:设所求的方程是
①
于是
即
②
③
④
消去 ,得
解此方程组,得
代入②式,得
待定系数法
交流合作
例2 的三个顶点分别是 求 的外接圆的标准方程.
1.圆心:两条弦的垂直平分线的交点
2.半径:圆心与圆上一点的距离
几何法:
小组合作任务:
1.如何求解上述方程组?
2.动手画一画:在学案例2给定的图形中,作出 的外接圆的圆心,并画出该圆.是否发现求解本题的新的方法?
(1)几何法
它是利用图形的几何性质,如圆的性质等,直接求出圆的圆心和半径,
代入圆的标准方程,从而得到圆的标准方程.
(2)待定系数法
由三个独立条件得到三个方程,解方程组以得到圆的标准方程中三个参数,从而确定圆的标准方程.它是求圆的方程最常用的方法,一般步骤是:
①设——设所求圆的方程为(x-a)2+(y-b)2=r2;
②列——由已知条件,建立关于a,b,r的方程组;
③解——解方程组,求出a,b,r;
④代——将a,b,r代入所设方程,得所求圆的方程.
求圆的标准方程的方法
争分夺秒
例3 已知圆心为 的圆经过 两点,且圆心 在直线
上,求此圆的标准方程.
方法一:几何法
方法二:待定系数法
解:设所求的方程是
①
规则:1.只需给出方法和思路,不求结果;
2.每种方法和思路,最先回答正确者获胜!
课堂小结
当堂检测
B
C
1.必做题:课本88页第3题;
2.选做题:课本88页第5题;
3.延伸写作:
查阅资料,形成“阿波罗尼斯圆”有关的小文章,并通过课本89页第9题进行验证!
作业布置
希望本节课的学习,能为你以后的数学学习起到推波助澜的作用!
