人教版数学8年级下册 第十七章 勾股定理 学案(含答案)
文档属性
| 名称 | 人教版数学8年级下册 第十七章 勾股定理 学案(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 102.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-25 07:06:34 | ||
图片预览


文档简介
小结
班级:_____________姓名:__________________组号:_________
一、知识梳理
1.根据右图:用数学语言表示勾股定理及逆定理。
2.结合以前所学的知识,写出一个命题,并把这个命题改为逆命题。
3.三角形的三边长分别为6,8,10,它的最短边上的高为( )
A.6 B.4.5 C.2.4 D.8
4.满足下列条件的三角形中,不是直角三角形的是( )
A.三个内角比为1∶2∶1 B.三边之比为1∶2∶
C.三边为2,3,4 D.三个内角比为1∶2∶3
5.直角三角形两边长分别为3和4,则第三条边为_____________。
6.在Rt△ABC中,∠B=90°。若a=1,b=2,则c=_____________。
7.已知△ABC中,∠A=90°,AC=6cm,BC=10cm,求AB的长。
二、综合运用
1.如图所示,Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求CD的长。
2.若△ABC的三边a、b、c满足a2+b2+c2+50=6a+8b+10c,求△ABC的面积。
三、课堂检测
1.在直角三角形ABC中,斜边AB=1,则AB的值是( )
A.2 B.4 C.6 D.8
2.如图,阴影部分的正方形边长是 ㎝。
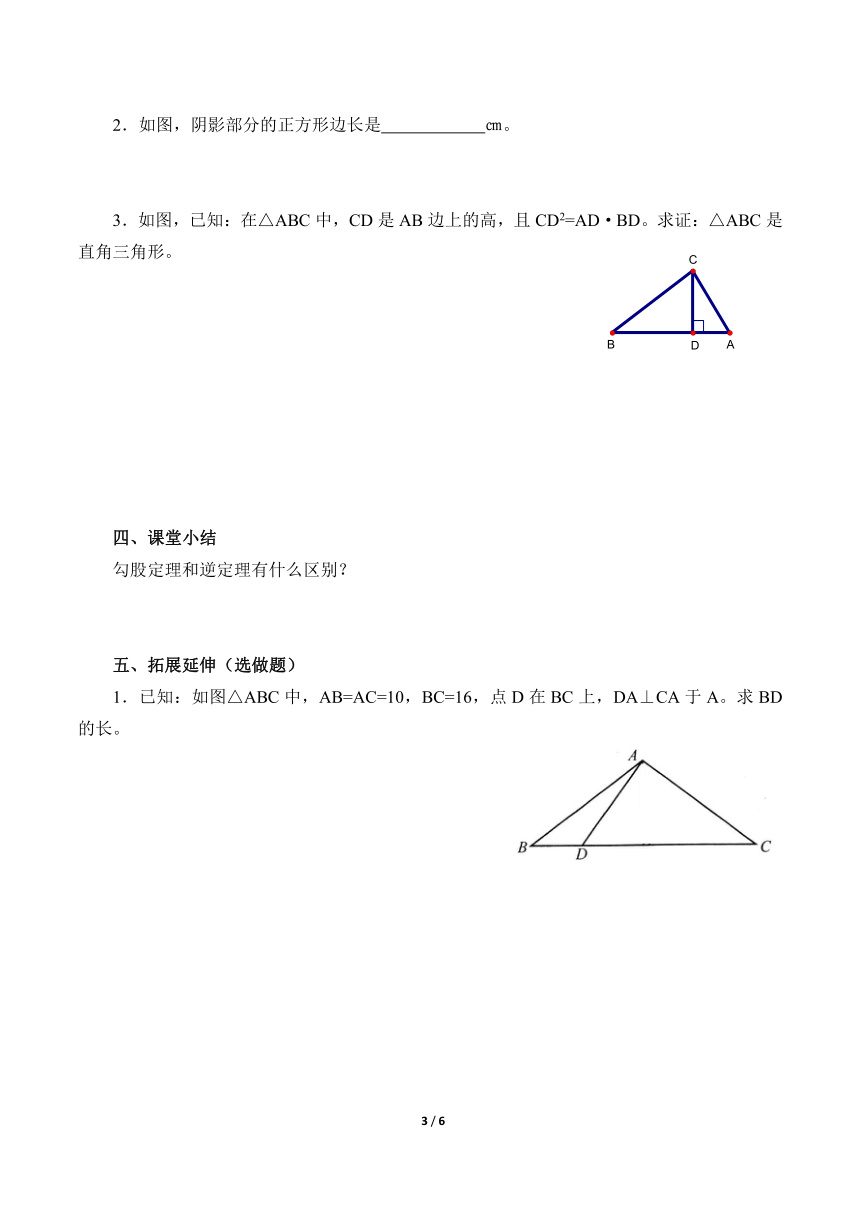
3.如图,已知:在△ABC中,CD是AB边上的高,且CD2=AD·BD。求证:△ABC是直角三角形。
四、课堂小结
勾股定理和逆定理有什么区别?
五、拓展延伸(选做题)
1.已知:如图△ABC中,AB=AC=10,BC=16,点D在BC上,DA⊥CA于A。求BD的长。
2.如图,某沿海城市A接到台风警报,在该市正南方向150km的B处有一台风中心正以20km/h的速度向BC方向移动,已知城市A到BC的距离AD=90km,那么
(1)台风中心经过多长时间从B点移到D点?
(2)如果在距台风中心30km的圆形区域内都有受到台风破坏的危险,为让D点的游人脱离危险,,游人必顺在接到台风警报后的几小时内撤离(撤离速度为6km/h)?最好选择什么方向?
【答案】
【知识梳理】
1.定理:
逆定理:
2.略
3.D
4.C
5.5或
6.
7.证明:∠A=90°,AC=6cm,BC=10cm,
由勾股定理得:
【综合运用】
1.解:∵△ABC是直角三角形,AC=6cm,BC=8cm,
由勾股定理得:∴AB===10cm,
∵△AED是△ACD翻折而成,
∴AE=AC=6cm,
设DE=CD=xcm,∠AED=90°,
∴BE=AB-AE=10-6=4cm,
在Rt△BDE中,BD2=DE2+BE2,
即(8-x)2=42+x2,
解得x=3.
故CD的长为3cm。
2.解:∵a2+b2+c2+50=6a+8b+10c
∴a2+b2+c2-6a-8b-10c+50=0,
∴a2-6a+9+b2-8b+16+c2-10c+25=0,
即(a-3)2+(b-4)2+(c-5)2=0,
∴a=3,b=4,c=5,
∵32+42=52,
∴△ABC是直角三角形;
S=×3×4=6
【课堂检测】
1.A
2.5
3.证明:∵CD⊥AB,
∴∠ADC=∠BDC=90°,
∴在RT△ACD中,根据勾股定理,得AC2=AD2+CD2,
在RT△ACD中,根据勾股定理,得BC2=CD2+BD2,
∴AC2+BC2=AD2+2CD2+BD2=AD2+2AD BD+BD2=(AD+BD)2=AB2,
∴∠ACB=90°。
∴△ABC总是直角三角形。
【课堂小结】
略
【拓展延伸】(选做题)
1.解:过点A作AE⊥BC与点E,
∵AB=AC=10,BC=16,
∴BE=CE=8,
在Rt△ACE中,利用勾股定理可知:AE==6,
设BD=x,则DE=8-x,DC=16-x,
又因为DA⊥CA,
在Rt△ADE和Rt△ADC中分别利用勾股定理得:AD2=AE2+DE2=DC2-AC2,
代入为:62+(8-x)2=(16-x)2-102,解得:x=,即DB=。
2.解:(1)在直角三角形ABD中,根据勾股定理,得BD==120.120÷20=6时;
(2)根据题意,得游人最好选择沿AD所在的方向撤离。撤离的时间=30÷6=5.
又台风到点D的时间是6小时。
即游人必须在接到台风警报后的1小时内撤离,撤离的方向最好是沿AD所在的方向。
A
B
C
D
6 / 6
班级:_____________姓名:__________________组号:_________
一、知识梳理
1.根据右图:用数学语言表示勾股定理及逆定理。
2.结合以前所学的知识,写出一个命题,并把这个命题改为逆命题。
3.三角形的三边长分别为6,8,10,它的最短边上的高为( )
A.6 B.4.5 C.2.4 D.8
4.满足下列条件的三角形中,不是直角三角形的是( )
A.三个内角比为1∶2∶1 B.三边之比为1∶2∶
C.三边为2,3,4 D.三个内角比为1∶2∶3
5.直角三角形两边长分别为3和4,则第三条边为_____________。
6.在Rt△ABC中,∠B=90°。若a=1,b=2,则c=_____________。
7.已知△ABC中,∠A=90°,AC=6cm,BC=10cm,求AB的长。
二、综合运用
1.如图所示,Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求CD的长。
2.若△ABC的三边a、b、c满足a2+b2+c2+50=6a+8b+10c,求△ABC的面积。
三、课堂检测
1.在直角三角形ABC中,斜边AB=1,则AB的值是( )
A.2 B.4 C.6 D.8
2.如图,阴影部分的正方形边长是 ㎝。
3.如图,已知:在△ABC中,CD是AB边上的高,且CD2=AD·BD。求证:△ABC是直角三角形。
四、课堂小结
勾股定理和逆定理有什么区别?
五、拓展延伸(选做题)
1.已知:如图△ABC中,AB=AC=10,BC=16,点D在BC上,DA⊥CA于A。求BD的长。
2.如图,某沿海城市A接到台风警报,在该市正南方向150km的B处有一台风中心正以20km/h的速度向BC方向移动,已知城市A到BC的距离AD=90km,那么
(1)台风中心经过多长时间从B点移到D点?
(2)如果在距台风中心30km的圆形区域内都有受到台风破坏的危险,为让D点的游人脱离危险,,游人必顺在接到台风警报后的几小时内撤离(撤离速度为6km/h)?最好选择什么方向?
【答案】
【知识梳理】
1.定理:
逆定理:
2.略
3.D
4.C
5.5或
6.
7.证明:∠A=90°,AC=6cm,BC=10cm,
由勾股定理得:
【综合运用】
1.解:∵△ABC是直角三角形,AC=6cm,BC=8cm,
由勾股定理得:∴AB===10cm,
∵△AED是△ACD翻折而成,
∴AE=AC=6cm,
设DE=CD=xcm,∠AED=90°,
∴BE=AB-AE=10-6=4cm,
在Rt△BDE中,BD2=DE2+BE2,
即(8-x)2=42+x2,
解得x=3.
故CD的长为3cm。
2.解:∵a2+b2+c2+50=6a+8b+10c
∴a2+b2+c2-6a-8b-10c+50=0,
∴a2-6a+9+b2-8b+16+c2-10c+25=0,
即(a-3)2+(b-4)2+(c-5)2=0,
∴a=3,b=4,c=5,
∵32+42=52,
∴△ABC是直角三角形;
S=×3×4=6
【课堂检测】
1.A
2.5
3.证明:∵CD⊥AB,
∴∠ADC=∠BDC=90°,
∴在RT△ACD中,根据勾股定理,得AC2=AD2+CD2,
在RT△ACD中,根据勾股定理,得BC2=CD2+BD2,
∴AC2+BC2=AD2+2CD2+BD2=AD2+2AD BD+BD2=(AD+BD)2=AB2,
∴∠ACB=90°。
∴△ABC总是直角三角形。
【课堂小结】
略
【拓展延伸】(选做题)
1.解:过点A作AE⊥BC与点E,
∵AB=AC=10,BC=16,
∴BE=CE=8,
在Rt△ACE中,利用勾股定理可知:AE==6,
设BD=x,则DE=8-x,DC=16-x,
又因为DA⊥CA,
在Rt△ADE和Rt△ADC中分别利用勾股定理得:AD2=AE2+DE2=DC2-AC2,
代入为:62+(8-x)2=(16-x)2-102,解得:x=,即DB=。
2.解:(1)在直角三角形ABD中,根据勾股定理,得BD==120.120÷20=6时;
(2)根据题意,得游人最好选择沿AD所在的方向撤离。撤离的时间=30÷6=5.
又台风到点D的时间是6小时。
即游人必须在接到台风警报后的1小时内撤离,撤离的方向最好是沿AD所在的方向。
A
B
C
D
6 / 6
