不等式

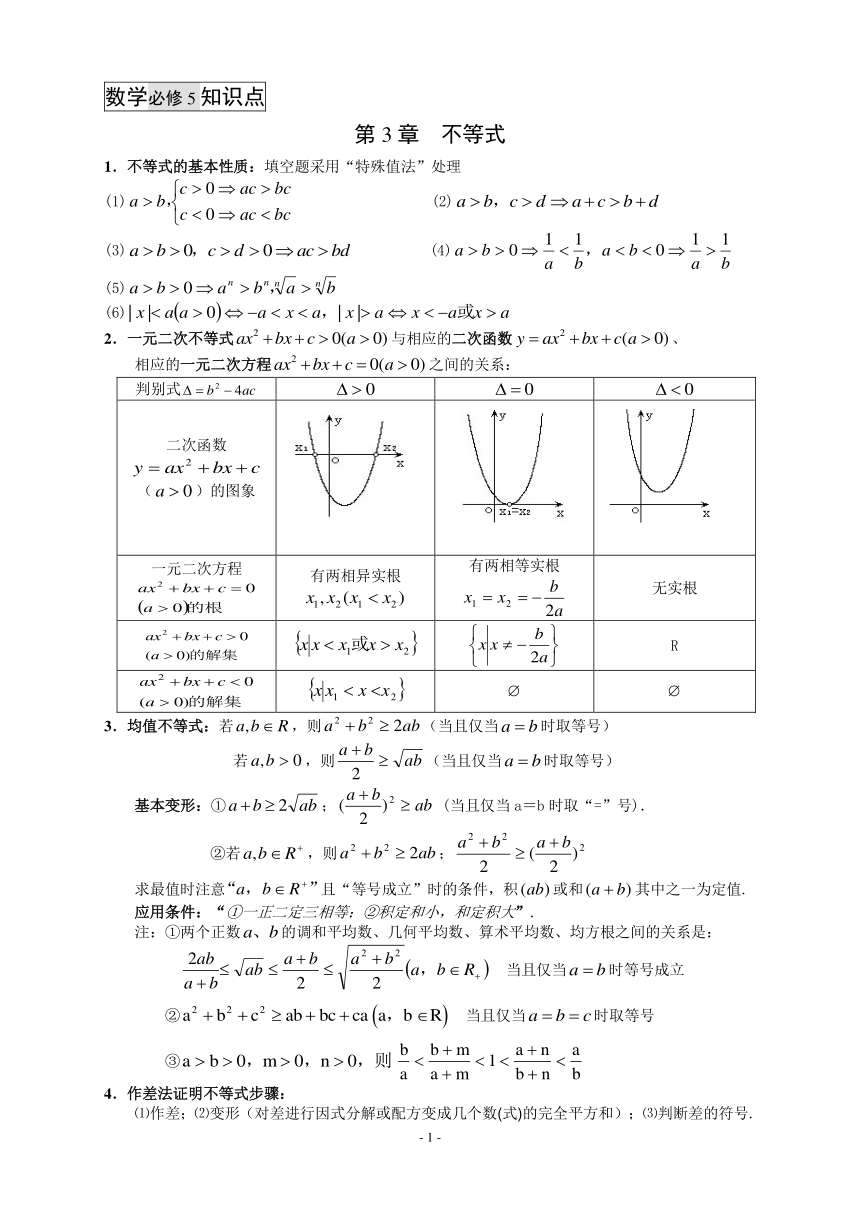
数学必修5知识点
第3章 不等式
1．不等式的基本性质：填空题采用“特殊值法”处理
(1) (2)
(3) (4)
(5)
(6)
2．一元二次不等式与相应的二次函数、
相应的一元二次方程之间的关系：
判别式
二次函数（）的图象
一元二次方程 有两相异实根 有两相等实根 无实根
R
3．均值不等式：若，则（当且仅当时取等号）
若，则（当且仅当时取等号）
基本变形：①； (当且仅当a＝b时取“=”号)．
②若，则；
求最值时注意且“等号成立”时的条件，积或和其中之一为定值.
应用条件：“①一正二定三相等；②积定和小，和定积大”.
注：①两个正数的调和平均数、几何平均数、算术平均数、均方根之间的关系是： 当且仅当时等号成立
② 当且仅当时取等号
③
4．作差法证明不等式步骤：
⑴作差；⑵变形（对差进行因式分解或配方变成几个数(式)的完全平方和）；⑶判断差的符号.
5．不等式的解法： 注意“系数化正”
(1)一元一次不等式：；
(2)一元二次不等式：
（“系数化正”，根据的三种情况（）写出解集．）
解一元二次不等式的步骤： （1）二次项系数化为正数；　 （2）解对应的一元二次方程；
（3）根据一元二次方程的根，结合不等号的方向画图；（4）写出不等式的解集．
一元二次不等式恒成立小结：
（）恒成立． （）恒成立
(3)绝对值不等式：若，则；
；
注：(ⅰ)去绝对值符号的方法：
1 平方法：通过两边平方去绝对值；需要注意的是不等号两边须为非负值.
2 讨论法：讨论绝对值中式子还是，然后去绝对值符号，转化为一般不等式.
③等价转化法：如或；.
(ⅱ)含有多个绝对值符号的不等式可用“按零点分区间讨论”的方法来解.
转化时利用 “零点分段法”（找零点，分段讨论，去掉绝对值符号，最后取各段的并集.）
如:解不等式，由两个零点及将R分为三段去掉绝对值再求解，
每一段的解都是不等式的解，最后取并集.
(ⅲ)绝对值不等式：
(4) 连不等式的转化：
(5) 分式不等式的解法：分式不等式变形为整式不等式；
⑴；⑵；
注：①分式不等式解法：
(移项通分,分子分母因式分解,的系数化为1，用穿轴法求结果)
②等价于且.对于“等号”要慎重处理.
(6)高次不等式：方法 “序轴标根法” (变形→标根→穿线→定解)
①不等式转化为(系数为1,根由小到大排列)，
②将分解为若干一次因式或二次不可分因式的乘积（使各括号内的系数为正），再将各根有序的标在数轴上，
③利用“奇穿偶回”(奇偶指幂指数的次数)的原则求解不等式.
用“穿轴法”解高次不等式技巧:“奇穿，偶切”（穿轴时从最大根的右上方开始）
如: 1. 解不等式，
解：原不等式等价于，
将方程的根标在轴上，
从右到左画出的示意图，∴原不等式的解集是或．
2.解不等式，
由图知不等式的解集为或或}，
(注意“等号”须单独考虑)
3.解不等式
(7)无理不等式：转化时把握二点：一是两边非负才能平方，二是根式必须有意义.
①等价于或；
②；
③；
④型，应按和进行分类.
(8)指数、对数不等式：转化时把握“同底数原则”“单调性原则”，同时还要注意真数大于零，底数要使不等式有意义.
①当时
；
②当时
；
(9)含参数的不等式：合理分类是关键，根据零根、根式有意义、影响不等号方向等因素确定分类标准，分类时要做到不重、不漏，然后求解并分类作答.
6．不等式表示的平面区域：
一般地，直线把平面分成两个区域：
表示直线及直线上方的平面区域；
表示直线及直线下方的平面区域．
注：对于不含边界的区域，要将边界画成虚线．
0
2
-1
-3
x
上半平面
下半平面
PAGE
- 2 -