人教版八年级上册12.2 三角形全等的判定 说课课件(共31张PPT)
文档属性
| 名称 | 人教版八年级上册12.2 三角形全等的判定 说课课件(共31张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-25 08:43:54 | ||
图片预览









文档简介
(共31张PPT)
*
12.2 三角形全等的判定
*
说 课 内 容
二、媒体
设计思路
一、教学设计思想
三、教学过程结构
*
一、教学设计思想
本课是探索三角形全等条件的第一课时,是在学习了全等三角形的概念和性质后展开的。它不仅是下节课探索三角形全等其它条件的基础,还是证明线段相等、角相等的重要依据,同时也为今后探索直角三角形全等的条件以及三角形相似的条件提供很好的模式和方法,为探究四边形,圆等相关知识做良好的铺垫。因此,本节课的知识具有承前启后的作用,占有相当重要的地位,自然也成为学生学好几何的切入点之一。
《新课标》指出,有效地数学活动不能单纯依赖模仿与记忆,动手实践,自主探索与合作交流,可以促进学生全面,持续,和谐的发展,是学生学习数学的重要方式。为此我在课堂教学中将尽量为学生提供“做中学”的时间和空间,让学生进行小组合作学习,在“做”的过程中潜移默化地渗透分类讨论的数学思想方法,遵循“教是为了不教”的原则,让学生自得知识、自寻方法、自觅规律、自悟原理。
*
教学目标:
1. 探究并掌握全等三角形的判定方法一:基本事实 “边边边”。
2.能应用上述基本事实解决问题,写出推理过程。
3.了解三角形的稳定性。
4.在活动中,培养学生的探究精神,合作能力,体会 数学与生活的联系,发现数学的美。
教学重点:
掌握并应用全等三角形的判定方法一:基本事实“边 边边”。
教学难点:
探究全等三角形的判定方法。
*
充分发挥交互式电子白板在课堂教学中的优势:屏幕批注,及时反馈;遮挡隐藏,分批呈现;拖放组合,灵活互动;模式切换,方便演示;智能绘图,提升效率等,在整个教学活动中,教师直观演示,学生主动参与。努力挖掘“白板”这一新交互平台中蕴含的教学策略,使这一技术真正融入到日常课堂教学中,实现信息技术与学科课程整合的新突破。
二、媒体设计思路
*
三、教学过程结构
课题:全等三角形的判定
开始
情景引入
活学活用
展示目标
总结反思
当堂训练
活动探究 1
活动探究 2
*
*
*
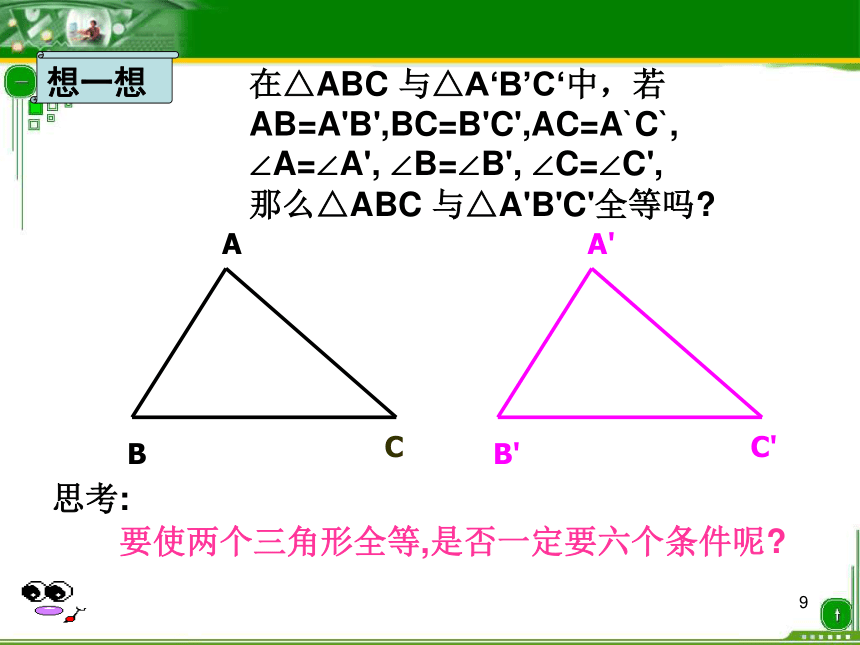
在△ABC 与△A‘B’C‘中,若AB=A'B',BC=B'C',AC=A`C`,
∠A=∠A', ∠B=∠B', ∠C=∠C',
那么△ABC 与△A'B'C'全等吗
A
B
C
A'
B'
C'
思考:
要使两个三角形全等,是否一定要六个条件呢
想一想
*
1.探究并掌握全等三角形的判定方法一:基本事实“边边 边”。
2.能应用上述基本事实解决问题,写出推理过程。
3.了解三角形的稳定性.
展示目标
*
满足下列条件的两个三角形是否一定全等:
(1)一个条件
(2)两个条件
(3)三个条件
一边
一角
两边
一边一角
两角
三角
三边
两边一角
两角一边
*
8cm
8cm
*
满足下列条件的两个三角形是否一定全等:
一边
一角
两边
一边一角
两角
三角
三边
两边一角
两角一边
×
(1)一个条件
(2)两个条件
(3)三个条件
*
400
400
*
满足下列条件的两个三角形是一定否全等:
一边
一角
两边
一边一角
两角
三角
三边
两边一角
两角一边
×
×
只有一个条件对应相等的两个三角形不一定全等。
(1)一个条件
(2)两个条件
(3)三个条件
*
300
9cm
300
9cm
300
9cm
300
9cm
300
9cm
*
满足下列条件的两个三角形是一定否全等:
一边
一角
两边
一边一角
两角
三角
三边
两边一角
两角一边
×
×
只有一个条件对应相等的两个三角形不一定全等。
×
(1)一个条件
(2)两个条件
(3)三个条件
*
300
500
300
500
*
满足下列条件的两个三角形是一定否全等:
一边
一角
两边
一边一角
两角
三角
三边
两边一角
两角一边
×
×
只有一个条件对应相等的两个三角形不一定全等。
×
×
(1)一个条件
(2)两个条件
(3)三个条件
*
8cm
9cm
8cm
9cm
*
满足下列条件的两个三角形是一定否全等:
一边
一角
两边
一边一角
两角
三角
三边
两边一角
两角一边
×
×
只有一个条件对应相等的两个三角形不一定全等。
×
×
×
只有两个条件对应相等的两个三角形不一定全等。
(1)一个条件
(2)两个条件
(3)三个条件
*
65度
35度
80度
65度
35度
80度
*
满足下列条件的两个三角形是一定否全等:
一边
一角
两边
一边一角
两角
三角
三边
两边一角
两角一边
×
×
只有一个条件对应相等的两个三角形不一定全等。
×
×
×
只有两个条件对应相等的两个三角形不一定全等。
×
(1)一个条件
(2)两个条件
(3)三个条件
*
如果两个三角形的三边对应相等,那么这两个三角形全等。(简记为“边边边”或“sss”)
想一想:由上述活动,你有什么发现?
1.用你手中的细铁丝折一个边长分别是3cm,4cm,6cm的三角形,把你做的三角形和小组内其他同学做出的三角形进行比较,它们能重合吗?
2.用你手中的细铁丝,余下1cm,用其余部分折一个边长分别是3cm,4cm,5cm的三角形,把你做的三角形和其他小组同学做出的三角形进行比较,它们能重合吗?
3.任取一组能构成三角形的三边长的数据(上面出现的除外),和小组内同学一起,画出这组数据构成的三角形,各组间比较所画三角形,它们能重合吗?
*
8cm
6cm
9cm
8cm
6cm
9cm
*
满足下列条件的两个三角形是否一定全等:
一个条件
两个条件
三个条件
一边
一角
两边
一边一角
两角
三角
三边
两边一角
两角一边
×
×
只有一个条件对应相等的两个三角形不一定全等。
×
×
×
只有两个条件对应相等的两个三角形不一定全等。
×
√
*
如果两个三角形的三边对应相等,那么这两个三角形全等。(简记为“边边边”或“sss”)
A
B
C
D
E
F
在△ABC和△ DEF中
∴ △ABC ≌△ DEF(SSS)
AB=DE
BC=EF
CA=FD
用符号语言表达为:
三角形全等判定方法1
*
木工师傅在做如图所示的门时,通常在门上角处斜钉两根木条,其中的道理是 .
三角形具有稳定性
*
已知:∠AOB
求作:∠A′O′B′=∠AOB
尺规作图:作一个角等于已知角
*
小结
本节课你有什么收获?有哪些体会?还有什么疑问?
*
谢谢大家!
*
12.2 三角形全等的判定
*
说 课 内 容
二、媒体
设计思路
一、教学设计思想
三、教学过程结构
*
一、教学设计思想
本课是探索三角形全等条件的第一课时,是在学习了全等三角形的概念和性质后展开的。它不仅是下节课探索三角形全等其它条件的基础,还是证明线段相等、角相等的重要依据,同时也为今后探索直角三角形全等的条件以及三角形相似的条件提供很好的模式和方法,为探究四边形,圆等相关知识做良好的铺垫。因此,本节课的知识具有承前启后的作用,占有相当重要的地位,自然也成为学生学好几何的切入点之一。
《新课标》指出,有效地数学活动不能单纯依赖模仿与记忆,动手实践,自主探索与合作交流,可以促进学生全面,持续,和谐的发展,是学生学习数学的重要方式。为此我在课堂教学中将尽量为学生提供“做中学”的时间和空间,让学生进行小组合作学习,在“做”的过程中潜移默化地渗透分类讨论的数学思想方法,遵循“教是为了不教”的原则,让学生自得知识、自寻方法、自觅规律、自悟原理。
*
教学目标:
1. 探究并掌握全等三角形的判定方法一:基本事实 “边边边”。
2.能应用上述基本事实解决问题,写出推理过程。
3.了解三角形的稳定性。
4.在活动中,培养学生的探究精神,合作能力,体会 数学与生活的联系,发现数学的美。
教学重点:
掌握并应用全等三角形的判定方法一:基本事实“边 边边”。
教学难点:
探究全等三角形的判定方法。
*
充分发挥交互式电子白板在课堂教学中的优势:屏幕批注,及时反馈;遮挡隐藏,分批呈现;拖放组合,灵活互动;模式切换,方便演示;智能绘图,提升效率等,在整个教学活动中,教师直观演示,学生主动参与。努力挖掘“白板”这一新交互平台中蕴含的教学策略,使这一技术真正融入到日常课堂教学中,实现信息技术与学科课程整合的新突破。
二、媒体设计思路
*
三、教学过程结构
课题:全等三角形的判定
开始
情景引入
活学活用
展示目标
总结反思
当堂训练
活动探究 1
活动探究 2
*
*
*
在△ABC 与△A‘B’C‘中,若AB=A'B',BC=B'C',AC=A`C`,
∠A=∠A', ∠B=∠B', ∠C=∠C',
那么△ABC 与△A'B'C'全等吗
A
B
C
A'
B'
C'
思考:
要使两个三角形全等,是否一定要六个条件呢
想一想
*
1.探究并掌握全等三角形的判定方法一:基本事实“边边 边”。
2.能应用上述基本事实解决问题,写出推理过程。
3.了解三角形的稳定性.
展示目标
*
满足下列条件的两个三角形是否一定全等:
(1)一个条件
(2)两个条件
(3)三个条件
一边
一角
两边
一边一角
两角
三角
三边
两边一角
两角一边
*
8cm
8cm
*
满足下列条件的两个三角形是否一定全等:
一边
一角
两边
一边一角
两角
三角
三边
两边一角
两角一边
×
(1)一个条件
(2)两个条件
(3)三个条件
*
400
400
*
满足下列条件的两个三角形是一定否全等:
一边
一角
两边
一边一角
两角
三角
三边
两边一角
两角一边
×
×
只有一个条件对应相等的两个三角形不一定全等。
(1)一个条件
(2)两个条件
(3)三个条件
*
300
9cm
300
9cm
300
9cm
300
9cm
300
9cm
*
满足下列条件的两个三角形是一定否全等:
一边
一角
两边
一边一角
两角
三角
三边
两边一角
两角一边
×
×
只有一个条件对应相等的两个三角形不一定全等。
×
(1)一个条件
(2)两个条件
(3)三个条件
*
300
500
300
500
*
满足下列条件的两个三角形是一定否全等:
一边
一角
两边
一边一角
两角
三角
三边
两边一角
两角一边
×
×
只有一个条件对应相等的两个三角形不一定全等。
×
×
(1)一个条件
(2)两个条件
(3)三个条件
*
8cm
9cm
8cm
9cm
*
满足下列条件的两个三角形是一定否全等:
一边
一角
两边
一边一角
两角
三角
三边
两边一角
两角一边
×
×
只有一个条件对应相等的两个三角形不一定全等。
×
×
×
只有两个条件对应相等的两个三角形不一定全等。
(1)一个条件
(2)两个条件
(3)三个条件
*
65度
35度
80度
65度
35度
80度
*
满足下列条件的两个三角形是一定否全等:
一边
一角
两边
一边一角
两角
三角
三边
两边一角
两角一边
×
×
只有一个条件对应相等的两个三角形不一定全等。
×
×
×
只有两个条件对应相等的两个三角形不一定全等。
×
(1)一个条件
(2)两个条件
(3)三个条件
*
如果两个三角形的三边对应相等,那么这两个三角形全等。(简记为“边边边”或“sss”)
想一想:由上述活动,你有什么发现?
1.用你手中的细铁丝折一个边长分别是3cm,4cm,6cm的三角形,把你做的三角形和小组内其他同学做出的三角形进行比较,它们能重合吗?
2.用你手中的细铁丝,余下1cm,用其余部分折一个边长分别是3cm,4cm,5cm的三角形,把你做的三角形和其他小组同学做出的三角形进行比较,它们能重合吗?
3.任取一组能构成三角形的三边长的数据(上面出现的除外),和小组内同学一起,画出这组数据构成的三角形,各组间比较所画三角形,它们能重合吗?
*
8cm
6cm
9cm
8cm
6cm
9cm
*
满足下列条件的两个三角形是否一定全等:
一个条件
两个条件
三个条件
一边
一角
两边
一边一角
两角
三角
三边
两边一角
两角一边
×
×
只有一个条件对应相等的两个三角形不一定全等。
×
×
×
只有两个条件对应相等的两个三角形不一定全等。
×
√
*
如果两个三角形的三边对应相等,那么这两个三角形全等。(简记为“边边边”或“sss”)
A
B
C
D
E
F
在△ABC和△ DEF中
∴ △ABC ≌△ DEF(SSS)
AB=DE
BC=EF
CA=FD
用符号语言表达为:
三角形全等判定方法1
*
木工师傅在做如图所示的门时,通常在门上角处斜钉两根木条,其中的道理是 .
三角形具有稳定性
*
已知:∠AOB
求作:∠A′O′B′=∠AOB
尺规作图:作一个角等于已知角
*
小结
本节课你有什么收获?有哪些体会?还有什么疑问?
*
谢谢大家!
