苏教版小学数学六年级上册3.8 《按比例分配的实际问题》 课件(共31张PPT)
文档属性
| 名称 | 苏教版小学数学六年级上册3.8 《按比例分配的实际问题》 课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-23 23:29:30 | ||
图片预览








文档简介
(共31张PPT)
第8课时 按比例分配的实际问题 小学数学 · 六年级(上) ·SJ
理解按比例分配的意义,掌握按比例分配实 际问题的结构特点和解答方法。
使学生经历用转化的策略来解决按比例分配
实际问题的过程,感受这类问题的数量关系, 能正确解答按比例分配的实际问题。
在练习中体验数学与生活实际的密切联系,培 养学生的数学应用意识,激发学生学习数学的 自信心。
01.
学习目标
L e a n i n g o bj e ctiv e s
1
3
2
培养数学思维能力和分析、解决问题的能力,提高 学生应用知识解决实际问题的能力。
掌握按比例分配问题的特征和解题方法。
根据给出的比确定部分与整体的关系,灵活解决问 题。
学习重点
学习难点
核心素养
02.
重点难点
L e a n i n g p o i n t s
课前导入
L e a d i n
小王和小李合作做生意,
每人都投资了10万元,年 底共挣了3万元,他们平
分了这些利润,第二年,
小王追加了5万,年底共
挣了4万,现在他们该怎
样来分这些利润才公平呢?
想 一 想
知识链接
k n o d g e li n k
母鸡和公鸡只数的比是4:3
甲数与乙数的比为3: 1
男生与女生的比是4: 5
药粉和水的质量比是1:10
的比,还
能知道什
么?
知识链接
k n o w l e d g e li n k
根据给出
学习任务一
按比分配
。 探究新知
p r e s e n t a t i o n
11 把30个方格涂上红色和黄色,使红色与黄色方格个数的比是3:2,
两种颜色各应涂多少格?先算一算,再涂一涂。
怎样理解“红色与 黄色方格数的比是 3:2”?
探究新知
p r e s e n t a t i o n
11 把30个方格涂上红色和黄色,使红色与黄色方格个数的比是
3:2,两种颜色各应涂多少格?先算一算,再涂一涂。
红色方块的个数占3份, 黄色方块的个数占2份。
两种方块共有5份。
红色与黄色方个数的比是3:2
探究新知
p r e s e n t a t i o n
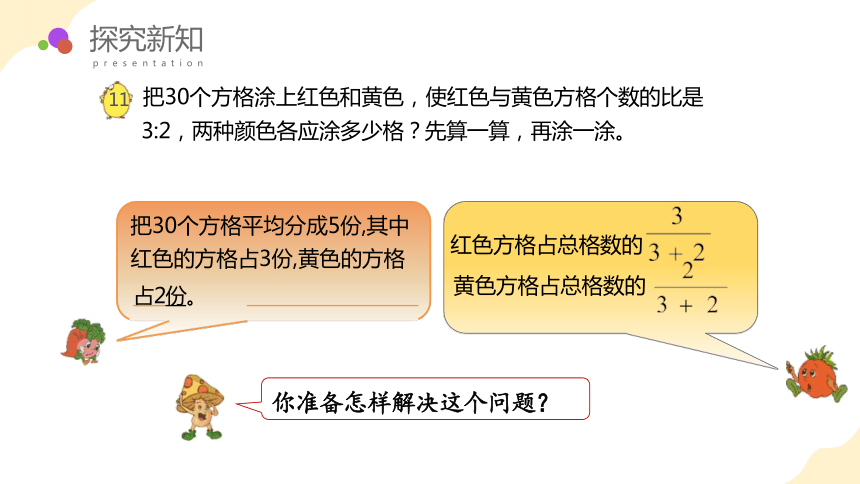
11 把30个方格涂上红色和黄色,使红色与黄色方格个数的比是
3:2,两种颜色各应涂多少格?先算一算,再涂一涂。
红色方块占总数的
黄色方块占总数的
黄色方块与总数的比为2: 5
红色方块与总数的比为3: 5
探究新知
p r e s e n t a t i o n
11 把30个方格涂上红色和黄色,使红色与黄色方格个数的比是
3:2,两种颜色各应涂多少格?先算一算,再涂一涂。
红色方格占总格数的 黄色方格占总格数的
把30个方格平均分成5份,其中
红色的方格占3份,黄色的方格 占2份。
你准备怎样解决这个问题?
探究新知
p r e s e n t a t i o n
11 把30个方格涂上红色和黄色,使红色与黄色方格个数的比是
3:2,两种颜色各应涂多少格?先算一算,再涂一涂。
30÷5=6 (格)
6×3=18 (格) 6×2=12 (格)
先求出一份有多少格,再算每种颜色的格数。
探究新知
p r e s e n t a t i o n
11 把30个方格涂上红色和黄色,使红色与黄色方格个数的比是
3:2,两种颜色各应涂多少格?先算一算,再涂一涂。
红色方格数占总格数的
30× = 30×
= 18 (格)
探究新知
p r e s e n t a t i o n
11 把30个方格涂上红色和黄色,使红色与黄色方格个数的比是
3:2,两种颜色各应涂多少格?先算一算,再涂一涂。
= 30×
= 12(格)
黄色方格数占总格数的
30×
探究新知
p r e s e n t a t i o n
11 把30个方格涂上红色和黄色,使红色与黄色方格个数的比是
3:2,两种颜色各应涂多少格?先算一算,再涂一涂。
①红色和黄色方格总数是否是30
18+12=30 (格)
②红色与黄色方格数的比是否是3:2
18: 12=3: 2
答:红色应涂18格,黄色应该涂12格。
该如何检验呢?
30个方格按1:2:3涂成红、黄、绿三种颜色,求三种颜色各 应涂多少格?
答:红色应涂5格,黄色应涂10格,绿色应涂15格。
30÷( 1+2+3) =5 (格)
探究新知
p r e s e n t a t i o n
5×2=10 (格)
5×3=15 (格)
5×1=5 (格)
(格)
(格) (格)
30个方格按1:2:3涂成红、黄、绿三种颜色,求三种颜色各 应涂多少格?
答:红色应涂5格,黄色应涂10格,绿色应涂15格。
红色:
黄色:
绿色:
各占总格数的多少?
探究新知
p r e s e n t a t i o n
学习任务二
按人数分配
怎样理解“植树棵数按各小 组人数的比分配”?
三个小组去植树,植树棵数按各小组人数的比分配。每个小组各应植树多
。 探究新知
p r e s e n t a t i o n
试一试
少棵?
方法一 总份数:8+7+9=24 每份:72÷24=3(棵) 一组:3×8=24(棵)
二组:3×7=21(棵)
三组:3×9=27(棵)
。 探究新知
p r e s e n t a t i o n
三个小组去植树,植树棵数按各小组人数的比分配。每个小组各应植 树多少棵?
“植树棵数按各小组人数的比分配”就是把72棵树按 8∶7∶9分到各个小组。
72棵树;一组8人;二组7人 ,三组9人
探究新知
p r e s e n t a t i o n
三个小组去植树,植树棵数按各小组人数的比分配。每个小组各应植
方法二:
72×
72×
72×
72棵树;一组8人;二组7人 ,三组9人
= 24 (棵)
= 21 (棵) = 27 (棵)
树多少棵?
已知:
1.总数量(两种或几种数量的和)
2.各部分量的比
求:
各部分的量。
。 探究新知
p r e s e n t a t i o n
按比例分配的实际问题的基本特征:
按比例分配实际问题的解题方法:
(1)把比的各项之和看成平均分的份数,先求出每份是多少,再解答。
解题步骤:求出总份数→求出每份是多少→求出各部分对应的具体数量。
(2)转化成分数乘法来解答,用总量乘每种量占总量的几分之几来计算。
解题步骤:根据比求出总份数→求出各部分的数量占总数量的几分之几→求出
各部分的数量。
探究新知
p r e s e n t a t i o n
学习任务三
达标检测,巩固练习
。 达标练习
p r a c t i c e
1.学校合唱队有48人,其中男生和女生人数的比是1:3。男、女 生各有多少人?
48× = 12 (人)
48× = 36 (人)
答:男生有12人、女生有36人。
35+31+24=90 (人)
180÷90×35=70 (块)
180÷90×31=62 (块)
180÷90×24=48 (块)
答:大、中、小班分别应分70块、 62块、 48块。
。 达标练习
p r a c t i c e
2.蓓蕾幼儿园大班有35人,中班有31人,小班有24人。张老师准备 把180块巧克力按班级人数的比分给3个班。每班各应分得多少块?
达标练习
p r a c t i c e
3.三角形的三个内角度数比为1: 2: 3, 这个三角形是什么三角形?
答:这是一个直角三角形。
180÷( 1+2+3) =180÷6=30 (度)
三角形内角和为180度。
30×1=30 (度)
30×2=60 (度)
30×3=90 (度)
。 达标练习
p r a c t i c e
4.( 2022秋.江苏镇江.期末) 一个长方形的周长是40米,长和宽的比是
4:1,长方形的面积是多少?
将长与宽的和按比例分配 ,所以分配的总量 是周长的一半
4×4=16 (米)
4×1=4 (米)
16×4=64 (平方米)
要算长方形的面积先要求出长和宽各是多少
40÷2÷(4+1) =20÷5=4 (米)
答:长方形的面积是64平方米。
达标练习
p r a c t i c e
5.大象最近开办了一家公司,小猪、小狗、狐狸因工作努力,大象决定拿出一笔钱,按4︰5︰6 奖赏给小猪、小狗、狐狸。 正当小猪、小狗想着自己拿钱的份数时,狐狸眼珠一转,说道:
“各位,为了计算简单一点,我们每人去掉自己三份的钱,按 1︰2︰3来分这笔钱,怎么样? 反正大家也没任何损失。 ”
600×4=2400 (元) 1500×1=1500 (元)
600×5=3000 (元)
1500×2=3000 (元)
9000÷(4+5+6) =9000÷15=600 (元) 9000÷( 1+2+3) =9000÷6=1500 (元)
以9000元奖金为例来计算
答:狐狸的说法不公平。
同学们 ,你们觉得狐狸说得有道理吗?
600×6=3600 (元)
1500×3=4500 (元)
1 知道总量和各种量的比,可以按比例进行分配。
2 可以用总量除以总份数求出每一份的量,然后用每份的量乘份数。
2 也可以用总量乘每种量占总量的几分之几来计算。
这节课你有什么收获?
知识总结
s u m m a r y
同学们再见
THANKS FOR WATCHING
第8课时 按比例分配的实际问题 小学数学 · 六年级(上) ·SJ
理解按比例分配的意义,掌握按比例分配实 际问题的结构特点和解答方法。
使学生经历用转化的策略来解决按比例分配
实际问题的过程,感受这类问题的数量关系, 能正确解答按比例分配的实际问题。
在练习中体验数学与生活实际的密切联系,培 养学生的数学应用意识,激发学生学习数学的 自信心。
01.
学习目标
L e a n i n g o bj e ctiv e s
1
3
2
培养数学思维能力和分析、解决问题的能力,提高 学生应用知识解决实际问题的能力。
掌握按比例分配问题的特征和解题方法。
根据给出的比确定部分与整体的关系,灵活解决问 题。
学习重点
学习难点
核心素养
02.
重点难点
L e a n i n g p o i n t s
课前导入
L e a d i n
小王和小李合作做生意,
每人都投资了10万元,年 底共挣了3万元,他们平
分了这些利润,第二年,
小王追加了5万,年底共
挣了4万,现在他们该怎
样来分这些利润才公平呢?
想 一 想
知识链接
k n o d g e li n k
母鸡和公鸡只数的比是4:3
甲数与乙数的比为3: 1
男生与女生的比是4: 5
药粉和水的质量比是1:10
的比,还
能知道什
么?
知识链接
k n o w l e d g e li n k
根据给出
学习任务一
按比分配
。 探究新知
p r e s e n t a t i o n
11 把30个方格涂上红色和黄色,使红色与黄色方格个数的比是3:2,
两种颜色各应涂多少格?先算一算,再涂一涂。
怎样理解“红色与 黄色方格数的比是 3:2”?
探究新知
p r e s e n t a t i o n
11 把30个方格涂上红色和黄色,使红色与黄色方格个数的比是
3:2,两种颜色各应涂多少格?先算一算,再涂一涂。
红色方块的个数占3份, 黄色方块的个数占2份。
两种方块共有5份。
红色与黄色方个数的比是3:2
探究新知
p r e s e n t a t i o n
11 把30个方格涂上红色和黄色,使红色与黄色方格个数的比是
3:2,两种颜色各应涂多少格?先算一算,再涂一涂。
红色方块占总数的
黄色方块占总数的
黄色方块与总数的比为2: 5
红色方块与总数的比为3: 5
探究新知
p r e s e n t a t i o n
11 把30个方格涂上红色和黄色,使红色与黄色方格个数的比是
3:2,两种颜色各应涂多少格?先算一算,再涂一涂。
红色方格占总格数的 黄色方格占总格数的
把30个方格平均分成5份,其中
红色的方格占3份,黄色的方格 占2份。
你准备怎样解决这个问题?
探究新知
p r e s e n t a t i o n
11 把30个方格涂上红色和黄色,使红色与黄色方格个数的比是
3:2,两种颜色各应涂多少格?先算一算,再涂一涂。
30÷5=6 (格)
6×3=18 (格) 6×2=12 (格)
先求出一份有多少格,再算每种颜色的格数。
探究新知
p r e s e n t a t i o n
11 把30个方格涂上红色和黄色,使红色与黄色方格个数的比是
3:2,两种颜色各应涂多少格?先算一算,再涂一涂。
红色方格数占总格数的
30× = 30×
= 18 (格)
探究新知
p r e s e n t a t i o n
11 把30个方格涂上红色和黄色,使红色与黄色方格个数的比是
3:2,两种颜色各应涂多少格?先算一算,再涂一涂。
= 30×
= 12(格)
黄色方格数占总格数的
30×
探究新知
p r e s e n t a t i o n
11 把30个方格涂上红色和黄色,使红色与黄色方格个数的比是
3:2,两种颜色各应涂多少格?先算一算,再涂一涂。
①红色和黄色方格总数是否是30
18+12=30 (格)
②红色与黄色方格数的比是否是3:2
18: 12=3: 2
答:红色应涂18格,黄色应该涂12格。
该如何检验呢?
30个方格按1:2:3涂成红、黄、绿三种颜色,求三种颜色各 应涂多少格?
答:红色应涂5格,黄色应涂10格,绿色应涂15格。
30÷( 1+2+3) =5 (格)
探究新知
p r e s e n t a t i o n
5×2=10 (格)
5×3=15 (格)
5×1=5 (格)
(格)
(格) (格)
30个方格按1:2:3涂成红、黄、绿三种颜色,求三种颜色各 应涂多少格?
答:红色应涂5格,黄色应涂10格,绿色应涂15格。
红色:
黄色:
绿色:
各占总格数的多少?
探究新知
p r e s e n t a t i o n
学习任务二
按人数分配
怎样理解“植树棵数按各小 组人数的比分配”?
三个小组去植树,植树棵数按各小组人数的比分配。每个小组各应植树多
。 探究新知
p r e s e n t a t i o n
试一试
少棵?
方法一 总份数:8+7+9=24 每份:72÷24=3(棵) 一组:3×8=24(棵)
二组:3×7=21(棵)
三组:3×9=27(棵)
。 探究新知
p r e s e n t a t i o n
三个小组去植树,植树棵数按各小组人数的比分配。每个小组各应植 树多少棵?
“植树棵数按各小组人数的比分配”就是把72棵树按 8∶7∶9分到各个小组。
72棵树;一组8人;二组7人 ,三组9人
探究新知
p r e s e n t a t i o n
三个小组去植树,植树棵数按各小组人数的比分配。每个小组各应植
方法二:
72×
72×
72×
72棵树;一组8人;二组7人 ,三组9人
= 24 (棵)
= 21 (棵) = 27 (棵)
树多少棵?
已知:
1.总数量(两种或几种数量的和)
2.各部分量的比
求:
各部分的量。
。 探究新知
p r e s e n t a t i o n
按比例分配的实际问题的基本特征:
按比例分配实际问题的解题方法:
(1)把比的各项之和看成平均分的份数,先求出每份是多少,再解答。
解题步骤:求出总份数→求出每份是多少→求出各部分对应的具体数量。
(2)转化成分数乘法来解答,用总量乘每种量占总量的几分之几来计算。
解题步骤:根据比求出总份数→求出各部分的数量占总数量的几分之几→求出
各部分的数量。
探究新知
p r e s e n t a t i o n
学习任务三
达标检测,巩固练习
。 达标练习
p r a c t i c e
1.学校合唱队有48人,其中男生和女生人数的比是1:3。男、女 生各有多少人?
48× = 12 (人)
48× = 36 (人)
答:男生有12人、女生有36人。
35+31+24=90 (人)
180÷90×35=70 (块)
180÷90×31=62 (块)
180÷90×24=48 (块)
答:大、中、小班分别应分70块、 62块、 48块。
。 达标练习
p r a c t i c e
2.蓓蕾幼儿园大班有35人,中班有31人,小班有24人。张老师准备 把180块巧克力按班级人数的比分给3个班。每班各应分得多少块?
达标练习
p r a c t i c e
3.三角形的三个内角度数比为1: 2: 3, 这个三角形是什么三角形?
答:这是一个直角三角形。
180÷( 1+2+3) =180÷6=30 (度)
三角形内角和为180度。
30×1=30 (度)
30×2=60 (度)
30×3=90 (度)
。 达标练习
p r a c t i c e
4.( 2022秋.江苏镇江.期末) 一个长方形的周长是40米,长和宽的比是
4:1,长方形的面积是多少?
将长与宽的和按比例分配 ,所以分配的总量 是周长的一半
4×4=16 (米)
4×1=4 (米)
16×4=64 (平方米)
要算长方形的面积先要求出长和宽各是多少
40÷2÷(4+1) =20÷5=4 (米)
答:长方形的面积是64平方米。
达标练习
p r a c t i c e
5.大象最近开办了一家公司,小猪、小狗、狐狸因工作努力,大象决定拿出一笔钱,按4︰5︰6 奖赏给小猪、小狗、狐狸。 正当小猪、小狗想着自己拿钱的份数时,狐狸眼珠一转,说道:
“各位,为了计算简单一点,我们每人去掉自己三份的钱,按 1︰2︰3来分这笔钱,怎么样? 反正大家也没任何损失。 ”
600×4=2400 (元) 1500×1=1500 (元)
600×5=3000 (元)
1500×2=3000 (元)
9000÷(4+5+6) =9000÷15=600 (元) 9000÷( 1+2+3) =9000÷6=1500 (元)
以9000元奖金为例来计算
答:狐狸的说法不公平。
同学们 ,你们觉得狐狸说得有道理吗?
600×6=3600 (元)
1500×3=4500 (元)
1 知道总量和各种量的比,可以按比例进行分配。
2 可以用总量除以总份数求出每一份的量,然后用每份的量乘份数。
2 也可以用总量乘每种量占总量的几分之几来计算。
这节课你有什么收获?
知识总结
s u m m a r y
同学们再见
THANKS FOR WATCHING
