第九章 9.4 乘法公式课件 47张PPT 苏科版数学七年级下册
文档属性
| 名称 | 第九章 9.4 乘法公式课件 47张PPT 苏科版数学七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-25 00:00:00 | ||
图片预览








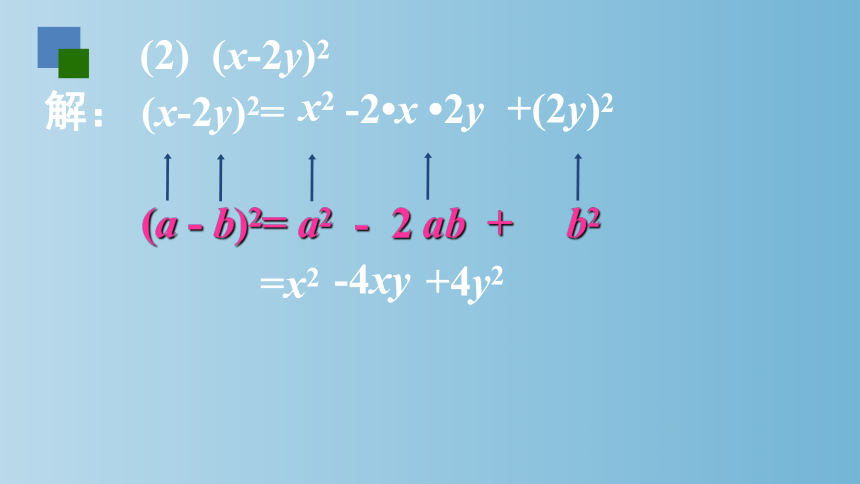



文档简介
(共47张PPT)
9.4乘法公式(1)
苏科版七年级下册 数学
聪明的阿凡提
从前有一个贪心的财主,人们叫他巴依老爷.巴依老爷有两块地,一块面积为a2,另一块面积为b2,而阿凡提只有一块地,面积为(a+b)2 .有一天,巴依老爷眼珠一转对阿凡提说:“我用我的两块地换你的一块地,可以吧?”
(1)你觉得阿凡提答应了吗?
(2)(a+b)2 与a2 + b2哪个大呢?
因需要将其边长增加 b 米。
一块边长为a米的正方形实验田,
形成四块实验田,以种植不同的新品
种(如图1—6).
a
a
b
b
图1—6
你能计算出现在这块实验田的面积吗
方法一、总面积=(a+b)2
方法二、总面积=a2+ab+ab+b2
=a2+2ab+b2
(a+b)2=a2+2ab+b2
你发现了什么?
(a+b)2=a2+2ab+b2
上面的等式是利用面积的不同表示形式得到的,你还有其他方法吗?
(a+b)2 =
(a+b)
(a+b)
=a2+ab+
ab+b2
=a2+2ab+
b2
一般的,对于任意的a ,b由多项式乘法法则同样可以得到
(a+b)2=a2+2ab+b2
完全平方公式
计算:( a – b )2
方法一:
解:(a-b)2= (a-b) (a-b)
=a2 –ab –ab +b2
=a2 -2ab +b2
方法二:
解:(a –b )2
=[a + (-b)]2
=a2 + 2a(-b) + (-b)2
= a2 -2ab + b2
(a –b )2 = a2 -2ab + b2
这也是完全平方公式哦
完全平方公式:
(a+b)2=a2 + 2ab + b2
(a-b)2=a2 - 2ab + b2
语言表述:两数和(差)的平方,等于它们的平方和加上(减去)它们乘积的两倍.
公式的结构特征:
首平方,尾平方,首尾两倍在中间,符号看前方.
例1 运用完全平方公式计算:
(1) (x+2y)2
解: (x+2y)2=
(a +b)2= a2 + 2 ab + b2
x2
+2 x 2y
+(2y)2
=x2
+4xy
+4y2
(2) (x-2y)2
解: (x-2y)2=
(a - b)2= a2 - 2 ab + b2
x2
-2 x 2y
+(2y)2
=x2
-4xy
+4y2
用完全平方公式计算
(3)( -x + 2y)2 (4) ( -2a - 5)2
方法一、原式=(2y-x)2
=(2y)2-2·2y·x+x2
=4y2-4xy+x2
方法二、原式=(-x)2+2·(-x) ·2y+(2y)2
=x2-4xy+4y2
=(2a+5)2
=(2a)2+2·2a·5+52
=4a2+20a+25
方法二、
原式=(-2a)2+2·(-2a) ·(-5)+(-5)2
=4a2+20a+25
(5) ( 4m2 - n2 )2
分析:
(a-b)2= a2 - 2ab+b2
4m2
a
n2
b
解:
( 4m2 - n2)2
=( )2-2( )·( )+( )2
4m2
4m2
n2
n2
=16m4-8m2n2+n4
(1)9982;
解:
(1) 9982 =(1000-2)2
=10002-2×1000×2+22
=1000000-4000+4
例2、运用乘法公式计算:
=996004
(2)20012
(2) 20012 =(2000 +1)2
=20002+2×2000×1+12
=4000000+4000+1=4004001
运用完全平方公式可以起到
简便运算的作用.
1、下面的计算是否正确?如有错误,请改正:
(1) (x+y)2=x2+y2;
(2) (-m+n)2=-m2 +n2;
(3) ( a 1)2= a2 2a 1.
解: (1)
×
应改为: (x+y)2= x2+2xy+y2
(2)× 第一项 应该是(-m)2 ,丢了一项
应改为: (-m+n)2= (-m)2+2 (-m)n +n2
=m2-2mn+n2
(3) ×
应改为:
( a 1)2=(a+1)2=a2+2a+1
2、填空:
(1) (a+_____)2=a2+4ab+4b2
(2) (3x-______)2=9x2-12xy+______
(3) (-x-_____)2=x2+______+1
3、小兵计算一个二项整式的平方式时,得到正确结果是4x2+ +25y2,但中间一项不慎被污染了,这一项应是( )
A 10xy B 20xy C±10xy D±20xy
2b
2y
4y2
1
2x
D
(2x 5y)2
±
(x+1)2
4、计算:(x2-2y2)2-(x2+2y2)2
解:原式=(x2)2-2·x2·2y2+(2y2)2 -[ (x2)2+2·x2·2y2+(2y2)2]
=x4-4x2y2+4y4-(x4+4x2y2+4y4)
=x4-4x2y2+4y4-x4-4x2y2-4y4
=-8x2y2
1、如何计算 (a+b+c)2
解: (a+b+c)2
=[(a+b)+c]2
=(a+b)2+2·(a+b)·c+c2
=a2+2ab+b2+2ac+2bc+c2
=a2+b2+c2+2ab+2ac+2bc
1、(a+b)2=(a-b)2 +_____
4ab
2、(a-b)2=(a+b)2 - _____
4ab
(a+b)2= a2+2ab + b2
(a –b)2 = a2 -2ab + b2
2、已知a+b=3,ab=1,求a2+b2、(a-b)2的值.
解:∵
(a+b)2=a2+2ab+b2
∴(a+b)2-2ab=a2+b2
即a2+b2=(a+b)2-2ab
∵a+b=3 ab=1
∴a2+b2=7
方法1、(a-b)2
=a2-2ab+b2=a2+b2-2ab
=5
方法2、
(a-b)2=(a+b)2-4ab
=5
=32-4
完全平方公式:
(a+b)2=a2+2ab+b2 ;
(a b)2=
a2 2ab+b2.
在解题过程中要准确确定a和b、对照公式原形的两边, 做到不丢项、不弄错符号、2ab时不少乘2
a2+b2=(a+b)2-2ab
(a-b)2=(a+b)2-4ab
(a+b)2=(a-b)2+4ab
9.4 乘法公式(2)
苏科版七年级下册 数学
完全平方公式:
(a+b)2=a2+2ab+b2
(a-b)2 = a2-2ab+b2
用乘法公式计算:
(1) (2a-3)2
(2) (-x+4y)2
(3) (-3a-1) 2
=4a2-12a+9
=16y2-8xy+x2
=9a2+6a+1
=(4y-x)2
=(3a+1)2
情境创设
边长为b 的小正方形纸片放置在边长为a 的大正方形纸片上,如右图,你能用多种方法求出阴影部分的面积吗?
b
a
a
b
方法(1)未被盖住的部分的面积为
b
a
a
b
b
b
a
a
方法(2):可以拼成等腰梯形,则未被盖住的部分的面积为
a
a
b
a
a
b
b
方法(3):可以拼成长方形,则未被盖住的部分的面积为
你能用多项式乘法运算法则推导所得到的公式吗?
解:(a+b)(a-b)=a2-ab+ab-b2
= a2-b2
一般地,对于任意的a、b,
这个公式称为平方差公式。
用语言叙述为:
两个数的和与这两个数的差的积等于这两个数的平方差.
判断下列各式能否运用平方差公式
√
√
√
√
√
√
×
×
例1.计算:
(1) (2x+3y)(2x-3y)=
(2) (-2x+3y)(-2x-3y)=
(3) (-2x+3y)(2x+3y)=
(4) (-2x-3y)(3x-2y)=
(5) (2x-3y)(3y-2x)=
(2x)2-(3y)2
=4x2-9y2
(-2x)2-(3y)2
=4x2-9y2
(3y-2x)(3y+2x)
=9y2-4x2
=(3y)2-(2x)2
-6x2+4xy-9xy+6y2
=-6x2-5xy+6y2
-(2x-3y)(2x-3y)
=-(2x-3y)2
=-(4x2-12xy+9y2)
=-4x2+12xy-9y2
例2.用简便方法计算:
=(100+1)(100-1)
=1002-12
=10000-1
=9999
101×99
例3、化简求值: (2x+y)( -y+2x) -(-2x-y)2, 其中x=-1,y=-2
解:原式=(2x+y)(2x-y)-(2x+y)2
=(2x)2-y2-(4x2+4xy+y2)
=4x2-y2-4x2-4xy-y2
=-2y2-4xy
当x=-1,y=-2时
原式=-2× (-2)2-4×(-1) ×(-2)
=-8-8=-16
填空:
(1) (m+____)(m-____)= m2-36n2
(2) (a+b)(______)= b2-a2
(3) (______)(1-x2)= x4-1
(4) 已知(x-ay)(x+ay)=x2-16y2, 那么a=____
6n
6n
b-a
-x2-1
±4
1.若x2-y2=8, y-x=4,求x+y.
解:∵(x+y)(x-y)=x2-y2
又x2-y2=8, y-x=4
∴(x+y) ×(-4)=8
∴x+y=-2
2、计算(x+3)(x-3)(x2+9)
原式=(x2-32)(x2+9)
=(x2)2-92
=x4-81
=(x2-9)(x2+9)
3.计算
原式=(22-1)(22+1)(24+1)(28+1)
=(24-1)(24+1)(28+1)
=(28-1)(28+1)
=216-1
(24)2=28
变式:
原式=(2-1)(2+1)(22+1)(24+1) ··· (21024+1)
=(22-1)(22+1)(24+1) ··· (21024+1)
=(21024-1)(21024+1)
= 22048-1
(22)2=24
=(21024)2-12
=(28)2-12
平方差公式
(a+b)(a-b)=a2-b2
9.4乘法公式(3)
苏科版七年级下册 数学
完全平方公式
平方差公式
(1) (a+b)2=a2+2ab+b2
(2) (a-b)2=a2-2ab+b2
(a+b)(a-b)=a2-b2
乘法公式
1.(2x-y)(_____)=4x2-y2
2.(b-a)(_____)=a2-b2
3. (______)2 =4x2-12xy+(____)
4.(-3x-2)(_____)=4-9x2
5.若x2+6x+m是完全平方式,则m=____
2x+y
-b-a
2x-3y
9y2
3x-2
6.若x2+mx+9是完全平方式,则m=____
9
±6
(x+__)2
3
(x 3)2
±
一、填空:
例1、计算
(1) (2x+3)(4x2+9)(2x-3)
原式= [(2x)2-32 ](4x2+9)
=(4x2-9)(4x2+9)
=(4x2)2-92
=16x4-81
(2)(x-y+1)(x+y-1)
原式=[x-(y-1) ] [ x+(y-1)]
=x2-(y-1)2
=x2-(y2-2·y·1+12)
=x2-(y2-2y+1)
=x2-y2+2y-1
(3) (a+3b)2(a-3b)2
原式=[(a+3b)(a-3b)]2
逆用积的乘方
=[a2-(3b)2]2
=(a2-9b2)2
=(a2)2-2·a2·9b2+(9b2)2
=a4-18a2b2+81b4
(4) (a+3b)2 - (a-3b)2
=(a2+6ab+9b2)-(a2-6ab+9b2)
= a2+6ab+9b2-a2+6ab-9b2
=12ab
原式=[ a2+2·a·3b+(3b)2]-[a2-2·a·3b+(3b)2 ]
(1) a2+b2=(a+b)2_____
(2) a2+b2=(a-b)2_____
(3) (a+b)2+(a-b)2=______
(4) (a+b)2-(a-b)2=______
(5) (a+b)2=(a-b)2______
(6) (a-b)2=(a+b)2______
-2ab
+2ab
2a2+2b2
4ab
+ 4ab
- 4ab
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
例2、已知 a+b=1,ab=-6.求a2+b2 ,
(a-b)2的值
解:由题意得
∴a2-12+b2=1
∴a2+b2=13
∵(a-b)2=(a+b)2-4ab
∴ (a-b)2=1-4(-6)=25
(a+b)2=12
∴a2+2ab+b2=1
方法2、
a2+b2=(a+b)2-2ab
=12-2×(-6)
=13
变式:已知(a+b)2=7,(a-b)2=3.
求:(1)a2+b2 (2)ab的值.
解∵(a+b)2=7,(a-b)2=3
∴a2+2ab+b2=7 ①
a2-2ab+b2=3 ②
∴①+②, 得:2a2+2b2=10
∴ a2+b2=5
①-②, 得:4ab=4
∴ab=1.
例3、已知(2a+2b+1)(2a+2b-1)=63,
求a+b的值.
解:∵ (2a+2b+1)(2a+2b-1)=63
∴(2a+2b)2-12=63
∴(2a+2b)2=64
∴2a+2b=±8
∴2(a+b)=±8
∴a+b=±4
变式:已知(a2+b2+1)(a2+b2-1)=63,求a2+b2的值.
解:∵ (a2+b2+1)(a2+b2-1)= 63
∴(a2+b2)2-12= 63
∴(a2+b2)2= 64
∴a2+b2=±8
∵a2+b2≥0
∴a2+b2= 8
例4、已知y2+1-2y+︱x-2︱=0,若x、y为等腰三角形的两边,求第三边的长。
解:∵y2+1-2y +︱x-2︱=0
∴y2-2y +12 +︱x-2︱=0
∴(y-1)2 +︱x-2︱=0
y-1=0
x-2=0
∴x=2
且
y=1
∵x、y为等腰三角形
∴三边为1、1、2或
∵三角形的任意两边之和大于第三边
的两边
2、2、1
∴三边为2、2、1,即 第三边为2
完全平方公式
平方差公式
乘法公式
(1) (a+b)2=a2+2ab+b2
(2) (a-b)2=a2-2ab+b2
(a+b)(a-b)=a2-b2
谢 谢 观 看
9.4乘法公式(1)
苏科版七年级下册 数学
聪明的阿凡提
从前有一个贪心的财主,人们叫他巴依老爷.巴依老爷有两块地,一块面积为a2,另一块面积为b2,而阿凡提只有一块地,面积为(a+b)2 .有一天,巴依老爷眼珠一转对阿凡提说:“我用我的两块地换你的一块地,可以吧?”
(1)你觉得阿凡提答应了吗?
(2)(a+b)2 与a2 + b2哪个大呢?
因需要将其边长增加 b 米。
一块边长为a米的正方形实验田,
形成四块实验田,以种植不同的新品
种(如图1—6).
a
a
b
b
图1—6
你能计算出现在这块实验田的面积吗
方法一、总面积=(a+b)2
方法二、总面积=a2+ab+ab+b2
=a2+2ab+b2
(a+b)2=a2+2ab+b2
你发现了什么?
(a+b)2=a2+2ab+b2
上面的等式是利用面积的不同表示形式得到的,你还有其他方法吗?
(a+b)2 =
(a+b)
(a+b)
=a2+ab+
ab+b2
=a2+2ab+
b2
一般的,对于任意的a ,b由多项式乘法法则同样可以得到
(a+b)2=a2+2ab+b2
完全平方公式
计算:( a – b )2
方法一:
解:(a-b)2= (a-b) (a-b)
=a2 –ab –ab +b2
=a2 -2ab +b2
方法二:
解:(a –b )2
=[a + (-b)]2
=a2 + 2a(-b) + (-b)2
= a2 -2ab + b2
(a –b )2 = a2 -2ab + b2
这也是完全平方公式哦
完全平方公式:
(a+b)2=a2 + 2ab + b2
(a-b)2=a2 - 2ab + b2
语言表述:两数和(差)的平方,等于它们的平方和加上(减去)它们乘积的两倍.
公式的结构特征:
首平方,尾平方,首尾两倍在中间,符号看前方.
例1 运用完全平方公式计算:
(1) (x+2y)2
解: (x+2y)2=
(a +b)2= a2 + 2 ab + b2
x2
+2 x 2y
+(2y)2
=x2
+4xy
+4y2
(2) (x-2y)2
解: (x-2y)2=
(a - b)2= a2 - 2 ab + b2
x2
-2 x 2y
+(2y)2
=x2
-4xy
+4y2
用完全平方公式计算
(3)( -x + 2y)2 (4) ( -2a - 5)2
方法一、原式=(2y-x)2
=(2y)2-2·2y·x+x2
=4y2-4xy+x2
方法二、原式=(-x)2+2·(-x) ·2y+(2y)2
=x2-4xy+4y2
=(2a+5)2
=(2a)2+2·2a·5+52
=4a2+20a+25
方法二、
原式=(-2a)2+2·(-2a) ·(-5)+(-5)2
=4a2+20a+25
(5) ( 4m2 - n2 )2
分析:
(a-b)2= a2 - 2ab+b2
4m2
a
n2
b
解:
( 4m2 - n2)2
=( )2-2( )·( )+( )2
4m2
4m2
n2
n2
=16m4-8m2n2+n4
(1)9982;
解:
(1) 9982 =(1000-2)2
=10002-2×1000×2+22
=1000000-4000+4
例2、运用乘法公式计算:
=996004
(2)20012
(2) 20012 =(2000 +1)2
=20002+2×2000×1+12
=4000000+4000+1=4004001
运用完全平方公式可以起到
简便运算的作用.
1、下面的计算是否正确?如有错误,请改正:
(1) (x+y)2=x2+y2;
(2) (-m+n)2=-m2 +n2;
(3) ( a 1)2= a2 2a 1.
解: (1)
×
应改为: (x+y)2= x2+2xy+y2
(2)× 第一项 应该是(-m)2 ,丢了一项
应改为: (-m+n)2= (-m)2+2 (-m)n +n2
=m2-2mn+n2
(3) ×
应改为:
( a 1)2=(a+1)2=a2+2a+1
2、填空:
(1) (a+_____)2=a2+4ab+4b2
(2) (3x-______)2=9x2-12xy+______
(3) (-x-_____)2=x2+______+1
3、小兵计算一个二项整式的平方式时,得到正确结果是4x2+ +25y2,但中间一项不慎被污染了,这一项应是( )
A 10xy B 20xy C±10xy D±20xy
2b
2y
4y2
1
2x
D
(2x 5y)2
±
(x+1)2
4、计算:(x2-2y2)2-(x2+2y2)2
解:原式=(x2)2-2·x2·2y2+(2y2)2 -[ (x2)2+2·x2·2y2+(2y2)2]
=x4-4x2y2+4y4-(x4+4x2y2+4y4)
=x4-4x2y2+4y4-x4-4x2y2-4y4
=-8x2y2
1、如何计算 (a+b+c)2
解: (a+b+c)2
=[(a+b)+c]2
=(a+b)2+2·(a+b)·c+c2
=a2+2ab+b2+2ac+2bc+c2
=a2+b2+c2+2ab+2ac+2bc
1、(a+b)2=(a-b)2 +_____
4ab
2、(a-b)2=(a+b)2 - _____
4ab
(a+b)2= a2+2ab + b2
(a –b)2 = a2 -2ab + b2
2、已知a+b=3,ab=1,求a2+b2、(a-b)2的值.
解:∵
(a+b)2=a2+2ab+b2
∴(a+b)2-2ab=a2+b2
即a2+b2=(a+b)2-2ab
∵a+b=3 ab=1
∴a2+b2=7
方法1、(a-b)2
=a2-2ab+b2=a2+b2-2ab
=5
方法2、
(a-b)2=(a+b)2-4ab
=5
=32-4
完全平方公式:
(a+b)2=a2+2ab+b2 ;
(a b)2=
a2 2ab+b2.
在解题过程中要准确确定a和b、对照公式原形的两边, 做到不丢项、不弄错符号、2ab时不少乘2
a2+b2=(a+b)2-2ab
(a-b)2=(a+b)2-4ab
(a+b)2=(a-b)2+4ab
9.4 乘法公式(2)
苏科版七年级下册 数学
完全平方公式:
(a+b)2=a2+2ab+b2
(a-b)2 = a2-2ab+b2
用乘法公式计算:
(1) (2a-3)2
(2) (-x+4y)2
(3) (-3a-1) 2
=4a2-12a+9
=16y2-8xy+x2
=9a2+6a+1
=(4y-x)2
=(3a+1)2
情境创设
边长为b 的小正方形纸片放置在边长为a 的大正方形纸片上,如右图,你能用多种方法求出阴影部分的面积吗?
b
a
a
b
方法(1)未被盖住的部分的面积为
b
a
a
b
b
b
a
a
方法(2):可以拼成等腰梯形,则未被盖住的部分的面积为
a
a
b
a
a
b
b
方法(3):可以拼成长方形,则未被盖住的部分的面积为
你能用多项式乘法运算法则推导所得到的公式吗?
解:(a+b)(a-b)=a2-ab+ab-b2
= a2-b2
一般地,对于任意的a、b,
这个公式称为平方差公式。
用语言叙述为:
两个数的和与这两个数的差的积等于这两个数的平方差.
判断下列各式能否运用平方差公式
√
√
√
√
√
√
×
×
例1.计算:
(1) (2x+3y)(2x-3y)=
(2) (-2x+3y)(-2x-3y)=
(3) (-2x+3y)(2x+3y)=
(4) (-2x-3y)(3x-2y)=
(5) (2x-3y)(3y-2x)=
(2x)2-(3y)2
=4x2-9y2
(-2x)2-(3y)2
=4x2-9y2
(3y-2x)(3y+2x)
=9y2-4x2
=(3y)2-(2x)2
-6x2+4xy-9xy+6y2
=-6x2-5xy+6y2
-(2x-3y)(2x-3y)
=-(2x-3y)2
=-(4x2-12xy+9y2)
=-4x2+12xy-9y2
例2.用简便方法计算:
=(100+1)(100-1)
=1002-12
=10000-1
=9999
101×99
例3、化简求值: (2x+y)( -y+2x) -(-2x-y)2, 其中x=-1,y=-2
解:原式=(2x+y)(2x-y)-(2x+y)2
=(2x)2-y2-(4x2+4xy+y2)
=4x2-y2-4x2-4xy-y2
=-2y2-4xy
当x=-1,y=-2时
原式=-2× (-2)2-4×(-1) ×(-2)
=-8-8=-16
填空:
(1) (m+____)(m-____)= m2-36n2
(2) (a+b)(______)= b2-a2
(3) (______)(1-x2)= x4-1
(4) 已知(x-ay)(x+ay)=x2-16y2, 那么a=____
6n
6n
b-a
-x2-1
±4
1.若x2-y2=8, y-x=4,求x+y.
解:∵(x+y)(x-y)=x2-y2
又x2-y2=8, y-x=4
∴(x+y) ×(-4)=8
∴x+y=-2
2、计算(x+3)(x-3)(x2+9)
原式=(x2-32)(x2+9)
=(x2)2-92
=x4-81
=(x2-9)(x2+9)
3.计算
原式=(22-1)(22+1)(24+1)(28+1)
=(24-1)(24+1)(28+1)
=(28-1)(28+1)
=216-1
(24)2=28
变式:
原式=(2-1)(2+1)(22+1)(24+1) ··· (21024+1)
=(22-1)(22+1)(24+1) ··· (21024+1)
=(21024-1)(21024+1)
= 22048-1
(22)2=24
=(21024)2-12
=(28)2-12
平方差公式
(a+b)(a-b)=a2-b2
9.4乘法公式(3)
苏科版七年级下册 数学
完全平方公式
平方差公式
(1) (a+b)2=a2+2ab+b2
(2) (a-b)2=a2-2ab+b2
(a+b)(a-b)=a2-b2
乘法公式
1.(2x-y)(_____)=4x2-y2
2.(b-a)(_____)=a2-b2
3. (______)2 =4x2-12xy+(____)
4.(-3x-2)(_____)=4-9x2
5.若x2+6x+m是完全平方式,则m=____
2x+y
-b-a
2x-3y
9y2
3x-2
6.若x2+mx+9是完全平方式,则m=____
9
±6
(x+__)2
3
(x 3)2
±
一、填空:
例1、计算
(1) (2x+3)(4x2+9)(2x-3)
原式= [(2x)2-32 ](4x2+9)
=(4x2-9)(4x2+9)
=(4x2)2-92
=16x4-81
(2)(x-y+1)(x+y-1)
原式=[x-(y-1) ] [ x+(y-1)]
=x2-(y-1)2
=x2-(y2-2·y·1+12)
=x2-(y2-2y+1)
=x2-y2+2y-1
(3) (a+3b)2(a-3b)2
原式=[(a+3b)(a-3b)]2
逆用积的乘方
=[a2-(3b)2]2
=(a2-9b2)2
=(a2)2-2·a2·9b2+(9b2)2
=a4-18a2b2+81b4
(4) (a+3b)2 - (a-3b)2
=(a2+6ab+9b2)-(a2-6ab+9b2)
= a2+6ab+9b2-a2+6ab-9b2
=12ab
原式=[ a2+2·a·3b+(3b)2]-[a2-2·a·3b+(3b)2 ]
(1) a2+b2=(a+b)2_____
(2) a2+b2=(a-b)2_____
(3) (a+b)2+(a-b)2=______
(4) (a+b)2-(a-b)2=______
(5) (a+b)2=(a-b)2______
(6) (a-b)2=(a+b)2______
-2ab
+2ab
2a2+2b2
4ab
+ 4ab
- 4ab
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
例2、已知 a+b=1,ab=-6.求a2+b2 ,
(a-b)2的值
解:由题意得
∴a2-12+b2=1
∴a2+b2=13
∵(a-b)2=(a+b)2-4ab
∴ (a-b)2=1-4(-6)=25
(a+b)2=12
∴a2+2ab+b2=1
方法2、
a2+b2=(a+b)2-2ab
=12-2×(-6)
=13
变式:已知(a+b)2=7,(a-b)2=3.
求:(1)a2+b2 (2)ab的值.
解∵(a+b)2=7,(a-b)2=3
∴a2+2ab+b2=7 ①
a2-2ab+b2=3 ②
∴①+②, 得:2a2+2b2=10
∴ a2+b2=5
①-②, 得:4ab=4
∴ab=1.
例3、已知(2a+2b+1)(2a+2b-1)=63,
求a+b的值.
解:∵ (2a+2b+1)(2a+2b-1)=63
∴(2a+2b)2-12=63
∴(2a+2b)2=64
∴2a+2b=±8
∴2(a+b)=±8
∴a+b=±4
变式:已知(a2+b2+1)(a2+b2-1)=63,求a2+b2的值.
解:∵ (a2+b2+1)(a2+b2-1)= 63
∴(a2+b2)2-12= 63
∴(a2+b2)2= 64
∴a2+b2=±8
∵a2+b2≥0
∴a2+b2= 8
例4、已知y2+1-2y+︱x-2︱=0,若x、y为等腰三角形的两边,求第三边的长。
解:∵y2+1-2y +︱x-2︱=0
∴y2-2y +12 +︱x-2︱=0
∴(y-1)2 +︱x-2︱=0
y-1=0
x-2=0
∴x=2
且
y=1
∵x、y为等腰三角形
∴三边为1、1、2或
∵三角形的任意两边之和大于第三边
的两边
2、2、1
∴三边为2、2、1,即 第三边为2
完全平方公式
平方差公式
乘法公式
(1) (a+b)2=a2+2ab+b2
(2) (a-b)2=a2-2ab+b2
(a+b)(a-b)=a2-b2
谢 谢 观 看
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
