数学人教A版(2019)必修第一册5.1.1任意角 课件(共24张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册5.1.1任意角 课件(共24张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-24 10:48:47 | ||
图片预览






文档简介
(共24张PPT)
5.1.1任意角
第五章 三角函数
情景引入,温故知新
现实世界中的许多运动、变化都有着循环往复、周而复始的规律, 这种变化规律称为周期性.例如: 地球自转引起的昼夜交替变化和公转引起的四季交替变化,月亮圆缺,潮汐变化,物体做匀速圆周运动时的位置变化,物体做简谐运动时的位移变化,交变电流变化等.这些现象都可以用三角函数刻画.
对比:初高中“角”的概念
角(初中):有公共端点的两条射线构成的几何图形.
角(高中):一条射线绕其端点按逆时针方向旋转形成的角叫做正角,按顺时针方向旋转形成的角叫做负角.如果一条射线没有做任何旋转,就称它形成了一个零角.这样,零角的始边与终边重合.如果是零角,那么
始边
终边
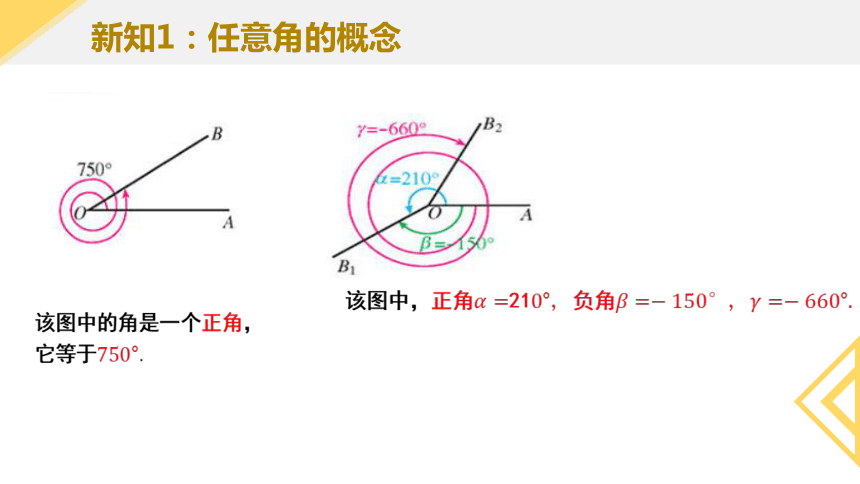
新知1:任意角的概念
该图中的角是一个正角,它等于.
该图中,正角21负角
时钟慢了1小时10分钟,
校准时分针要___时针旋转____°
主动轮逆时针旋转80°
被动轮顺时针旋转80°
顺
420
新知1:任意角的概念
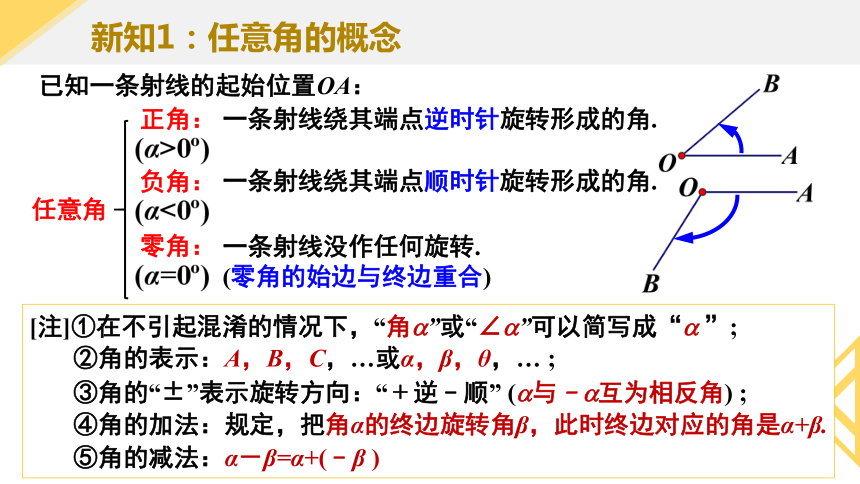
新知1:任意角的概念
正角:
负角:
一条射线绕其端点顺时针旋转形成的角.
一条射线绕其端点逆时针旋转形成的角.
零角:
一条射线没作任何旋转.
(零角的始边与终边重合)
任意角
已知一条射线的起始位置OA:
[注]①在不引起混淆的情况下,“角 ”或“∠ ”可以简写成“ ”;
②角的表示:A,B,C,…或α,β,θ,… ;
③角的“±”表示旋转方向:“﹢逆﹣顺” ( 与﹣ 互为相反角) ;
④角的加法:规定,把角α的终边旋转角β,此时终边对应的角是α+β.
⑤角的减法:α-β=α+(﹣β )
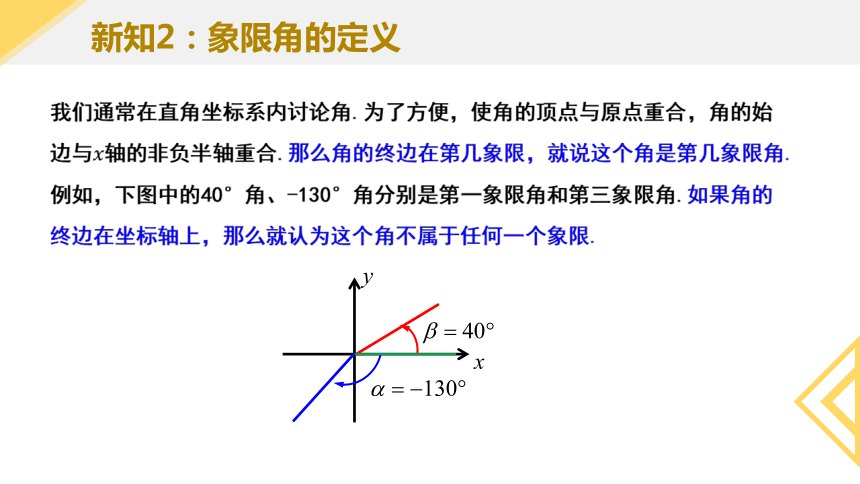
新知2:象限角的定义
我们通常在直角坐标系内讨论角.为了方便,使角的顶点与原点重合,角的始边与轴的非负半轴重合.那么角的终边在第几象限,就说这个角是第几象限角.例如,下图中的40°角、-130°角分别是第一象限角和第三象限角.如果角的终边在坐标轴上,那么就认为这个角不属于任何一个象限.
新知3:终边相同的角
问题:在直角坐标系中,给定一个角,则该角对应的终边唯一确定;
反之,若给定终边位置OB,则该终边对应的角唯一吗?
不难发现,在图中,如果-32°角的终边是,那么328°,-392°,…角的终边都是,并且与-32°角终边相同的这些角都可以表示成-32°的角与个周角的和,如:
与角α终边相同的所有角组成的集合:
象限角的集合表示:
象限角 角的集合表示
第一象限角
第二象限角
第三象限角
第四象限角
新知3:终边相同的角
【例1】每周一的早晨,我们都会在学校的操场上举行升国旗仪式,一般需要10分钟.这10分钟的时间,钟表的分针走过的角度是( )
A. B. C. D.
【答案】D
【解析】分针是顺时针走的,
形成的角度是负角,
又分针走过了10分钟,
走过的角度大小为,
综上,分针走过的角度是.
故选:D.
题型一:角的概念
【对点训练1】射线绕端点逆时针旋转到达位置,由位置绕端点旋转到达位置,得,则射线旋转的方向与角度分别为( )
A.逆时针, B.顺时针, C.逆时针, D.顺时针,
【答案】B
【解析】由题意可得,
设,
则,
解得,
所以射线绕端点顺时针旋转,
故选:B
题型一:角的概念
【对点训练2】下列说法正确的有几个( )
(1)第一象限的角都是锐角;(2)锐角都是第一象限的角;(3)锐角是大于小于的角;
A.0个 B.1个 C.2个 D.3个
【答案】C
【解析】第一象限角的集合为
,
锐角是大于小于的角,
锐角的集合为,所以(1)错误,(2)正确,(3)正确,
故选:C.
题型一:角的概念
【例2】在区间内找出与下列各角终边相同的角,并判定它是第几象限角.
(1);
(2);
(3).
【解析】(1)因为,
所以在区间内,与角终边相同的角是280°,它是第四象限角.
(2)因为,
所以在区间内,与1600°角终边相同的角是160°,它是第二象限角.
(3)因为,
所以在区间内,与角终边相同的角是,它是第三象限角.
题型二:终边相同的角的表示
【对点训练3】写出与下列各角终边相同的角的集合,并把集合中适合不等式的元素写出来:
(1); (2); (3); (4).
【解析】(1)与终边相同的角的集合为,
由,可得,
当时,;当时,,当时,,
所以,适合不等式的元素为、、.
(2)因为,所以,与终边相同的角的集合为,
由,可得,
当时,;当时,;当时,,
所以,适合不等式的元素为、、.
(3)因为,
所以,与终边相同的角的集合为,
由,可得、、,
当时,;当时,;当时,,
所以,适合不等式的元素为、、.
(4)因为,所以,与终边相同的角的集合为,
由,可得,
当时,;当时,;当时,.
所以,适合不等式的元素为、、.
题型二:终边相同的角的表示
【例3】若角是第二象限角,试确定角,是第几象限角.
【解析】因为是第二象限角,所以,
可得,
所以可能是第三象限角、第四象限角或终边在轴非正半轴上的角.
又由 ,当时,
,此时是第一象限角;
当时,,此时是第二象限角;
当时,,此时是第四象限角.
综上所述,可能是第一象限角、第二象限角或第四象限角.
题型三:角所在象限的研究
【对点训练4】若,,试确定,分别是第几象限角.
【解析】由得:,
为第一象限角;
由得:,
当时,,
则为第一象限角;
当时,,
则为第三象限角;
综上所述:为第一象限角;为第一或第三象限角.
题型三:角所在象限的研究
【例4】若是第二象限角,则是( )
A.第一象限角 B.第二象限角 C.第三象限角 D.第四象限角
【答案】D
【解析】由题意是第二象限角,
所以不妨设,
所以,
由象限角的定义可知是第四象限角.
故选:D.
题型四:象限角的判定
【对点训练5】若是第一象限角,则下列各角是第三象限角的是( )
A. B. C. D.
【答案】C
【解析】若是第一象限角,
则,
,
则是第四象限角,故D错误;
,
则是第一象限角,故A错误;
,则是第二象限角,故B错误;
,则是第三象限角,故C错误.
故选:C.
题型四:象限角的判定
【对点训练6】若为第二象限角,则的终边所在的象限是( )
A.第二象限 B.第一、二象限 C.第一、三象限 D.第二、四象限
【答案】D
【解析】因为为第二象限角,
则,
因此,
而为偶数,当为奇数时,为奇数,则为第四象限角,
当为偶数时,为偶数,则为第二象限角,
所以的终边所在的象限是第二、四象限.
故选:D
题型四:象限角的判定
【例5】分别表示终边落在如图(1)(2)所示的阴影部分内(不包括边界)的角的集合.(如无特别说明,边界线为实线代表包括边界,边界线为虚线代表不包括边界)
【解析】(1)角的终边可以看作是角的终边,角的终边,
所以终边落在阴影部分内(不包括边界)的角的集合为.
(2)与(1)类似可写出终边落在阴影部分内(不包括边界)的角的集合为
.
题型五:区域角的表示
【对点训练7】如图,阴影部分表示角的终边所在的位置,试写出角的集合.
【解析】(1)①
;
②.
题型五:区域角的表示
小结提升,形成结构
请你带着下列问题回顾本节课学习的内容:
(1)任意角的概念;
(2)象限角与终边相同的角;
(3)象限角及轴线角的集合表示.
布置作业,应用迁移
作业:教科书第175页习题5.1第1、2题.
好学数学
数学好学
学好数学
5.1.1任意角
第五章 三角函数
情景引入,温故知新
现实世界中的许多运动、变化都有着循环往复、周而复始的规律, 这种变化规律称为周期性.例如: 地球自转引起的昼夜交替变化和公转引起的四季交替变化,月亮圆缺,潮汐变化,物体做匀速圆周运动时的位置变化,物体做简谐运动时的位移变化,交变电流变化等.这些现象都可以用三角函数刻画.
对比:初高中“角”的概念
角(初中):有公共端点的两条射线构成的几何图形.
角(高中):一条射线绕其端点按逆时针方向旋转形成的角叫做正角,按顺时针方向旋转形成的角叫做负角.如果一条射线没有做任何旋转,就称它形成了一个零角.这样,零角的始边与终边重合.如果是零角,那么
始边
终边
新知1:任意角的概念
该图中的角是一个正角,它等于.
该图中,正角21负角
时钟慢了1小时10分钟,
校准时分针要___时针旋转____°
主动轮逆时针旋转80°
被动轮顺时针旋转80°
顺
420
新知1:任意角的概念
新知1:任意角的概念
正角:
负角:
一条射线绕其端点顺时针旋转形成的角.
一条射线绕其端点逆时针旋转形成的角.
零角:
一条射线没作任何旋转.
(零角的始边与终边重合)
任意角
已知一条射线的起始位置OA:
[注]①在不引起混淆的情况下,“角 ”或“∠ ”可以简写成“ ”;
②角的表示:A,B,C,…或α,β,θ,… ;
③角的“±”表示旋转方向:“﹢逆﹣顺” ( 与﹣ 互为相反角) ;
④角的加法:规定,把角α的终边旋转角β,此时终边对应的角是α+β.
⑤角的减法:α-β=α+(﹣β )
新知2:象限角的定义
我们通常在直角坐标系内讨论角.为了方便,使角的顶点与原点重合,角的始边与轴的非负半轴重合.那么角的终边在第几象限,就说这个角是第几象限角.例如,下图中的40°角、-130°角分别是第一象限角和第三象限角.如果角的终边在坐标轴上,那么就认为这个角不属于任何一个象限.
新知3:终边相同的角
问题:在直角坐标系中,给定一个角,则该角对应的终边唯一确定;
反之,若给定终边位置OB,则该终边对应的角唯一吗?
不难发现,在图中,如果-32°角的终边是,那么328°,-392°,…角的终边都是,并且与-32°角终边相同的这些角都可以表示成-32°的角与个周角的和,如:
与角α终边相同的所有角组成的集合:
象限角的集合表示:
象限角 角的集合表示
第一象限角
第二象限角
第三象限角
第四象限角
新知3:终边相同的角
【例1】每周一的早晨,我们都会在学校的操场上举行升国旗仪式,一般需要10分钟.这10分钟的时间,钟表的分针走过的角度是( )
A. B. C. D.
【答案】D
【解析】分针是顺时针走的,
形成的角度是负角,
又分针走过了10分钟,
走过的角度大小为,
综上,分针走过的角度是.
故选:D.
题型一:角的概念
【对点训练1】射线绕端点逆时针旋转到达位置,由位置绕端点旋转到达位置,得,则射线旋转的方向与角度分别为( )
A.逆时针, B.顺时针, C.逆时针, D.顺时针,
【答案】B
【解析】由题意可得,
设,
则,
解得,
所以射线绕端点顺时针旋转,
故选:B
题型一:角的概念
【对点训练2】下列说法正确的有几个( )
(1)第一象限的角都是锐角;(2)锐角都是第一象限的角;(3)锐角是大于小于的角;
A.0个 B.1个 C.2个 D.3个
【答案】C
【解析】第一象限角的集合为
,
锐角是大于小于的角,
锐角的集合为,所以(1)错误,(2)正确,(3)正确,
故选:C.
题型一:角的概念
【例2】在区间内找出与下列各角终边相同的角,并判定它是第几象限角.
(1);
(2);
(3).
【解析】(1)因为,
所以在区间内,与角终边相同的角是280°,它是第四象限角.
(2)因为,
所以在区间内,与1600°角终边相同的角是160°,它是第二象限角.
(3)因为,
所以在区间内,与角终边相同的角是,它是第三象限角.
题型二:终边相同的角的表示
【对点训练3】写出与下列各角终边相同的角的集合,并把集合中适合不等式的元素写出来:
(1); (2); (3); (4).
【解析】(1)与终边相同的角的集合为,
由,可得,
当时,;当时,,当时,,
所以,适合不等式的元素为、、.
(2)因为,所以,与终边相同的角的集合为,
由,可得,
当时,;当时,;当时,,
所以,适合不等式的元素为、、.
(3)因为,
所以,与终边相同的角的集合为,
由,可得、、,
当时,;当时,;当时,,
所以,适合不等式的元素为、、.
(4)因为,所以,与终边相同的角的集合为,
由,可得,
当时,;当时,;当时,.
所以,适合不等式的元素为、、.
题型二:终边相同的角的表示
【例3】若角是第二象限角,试确定角,是第几象限角.
【解析】因为是第二象限角,所以,
可得,
所以可能是第三象限角、第四象限角或终边在轴非正半轴上的角.
又由 ,当时,
,此时是第一象限角;
当时,,此时是第二象限角;
当时,,此时是第四象限角.
综上所述,可能是第一象限角、第二象限角或第四象限角.
题型三:角所在象限的研究
【对点训练4】若,,试确定,分别是第几象限角.
【解析】由得:,
为第一象限角;
由得:,
当时,,
则为第一象限角;
当时,,
则为第三象限角;
综上所述:为第一象限角;为第一或第三象限角.
题型三:角所在象限的研究
【例4】若是第二象限角,则是( )
A.第一象限角 B.第二象限角 C.第三象限角 D.第四象限角
【答案】D
【解析】由题意是第二象限角,
所以不妨设,
所以,
由象限角的定义可知是第四象限角.
故选:D.
题型四:象限角的判定
【对点训练5】若是第一象限角,则下列各角是第三象限角的是( )
A. B. C. D.
【答案】C
【解析】若是第一象限角,
则,
,
则是第四象限角,故D错误;
,
则是第一象限角,故A错误;
,则是第二象限角,故B错误;
,则是第三象限角,故C错误.
故选:C.
题型四:象限角的判定
【对点训练6】若为第二象限角,则的终边所在的象限是( )
A.第二象限 B.第一、二象限 C.第一、三象限 D.第二、四象限
【答案】D
【解析】因为为第二象限角,
则,
因此,
而为偶数,当为奇数时,为奇数,则为第四象限角,
当为偶数时,为偶数,则为第二象限角,
所以的终边所在的象限是第二、四象限.
故选:D
题型四:象限角的判定
【例5】分别表示终边落在如图(1)(2)所示的阴影部分内(不包括边界)的角的集合.(如无特别说明,边界线为实线代表包括边界,边界线为虚线代表不包括边界)
【解析】(1)角的终边可以看作是角的终边,角的终边,
所以终边落在阴影部分内(不包括边界)的角的集合为.
(2)与(1)类似可写出终边落在阴影部分内(不包括边界)的角的集合为
.
题型五:区域角的表示
【对点训练7】如图,阴影部分表示角的终边所在的位置,试写出角的集合.
【解析】(1)①
;
②.
题型五:区域角的表示
小结提升,形成结构
请你带着下列问题回顾本节课学习的内容:
(1)任意角的概念;
(2)象限角与终边相同的角;
(3)象限角及轴线角的集合表示.
布置作业,应用迁移
作业:教科书第175页习题5.1第1、2题.
好学数学
数学好学
学好数学
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
