数学人教A版(2019)选择性必修第一册1.3.1空间直角坐标系 课件(共26张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册1.3.1空间直角坐标系 课件(共26张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 822.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-24 15:26:06 | ||
图片预览



文档简介
(共26张PPT)
1.3.1 空间直角坐标系
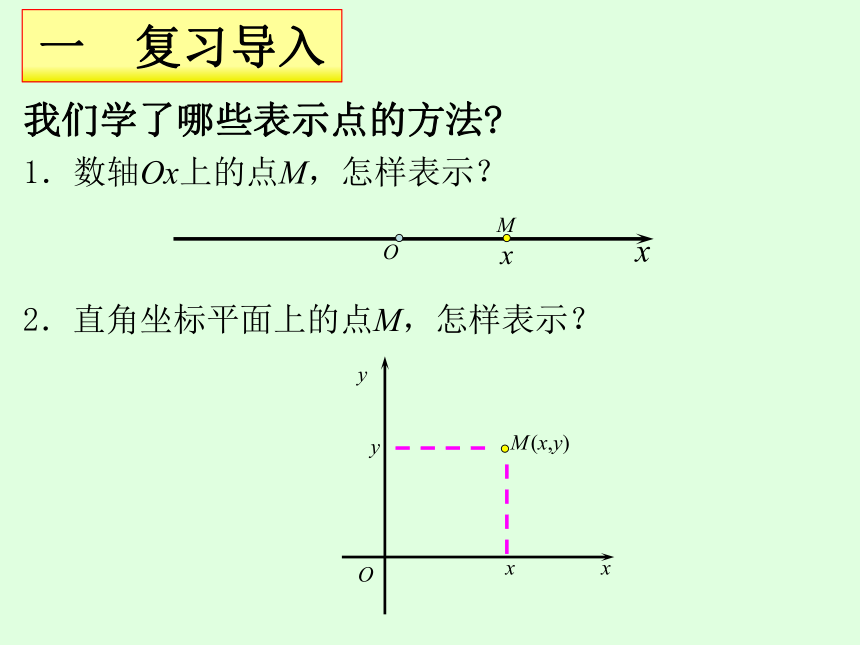
1.数轴Ox上的点M,怎样表示?
2.直角坐标平面上的点M,怎样表示?
x
O
x
M
x
O
y
M
(x,y)
x
y
我们学了哪些表示点的方法
一 复习导入
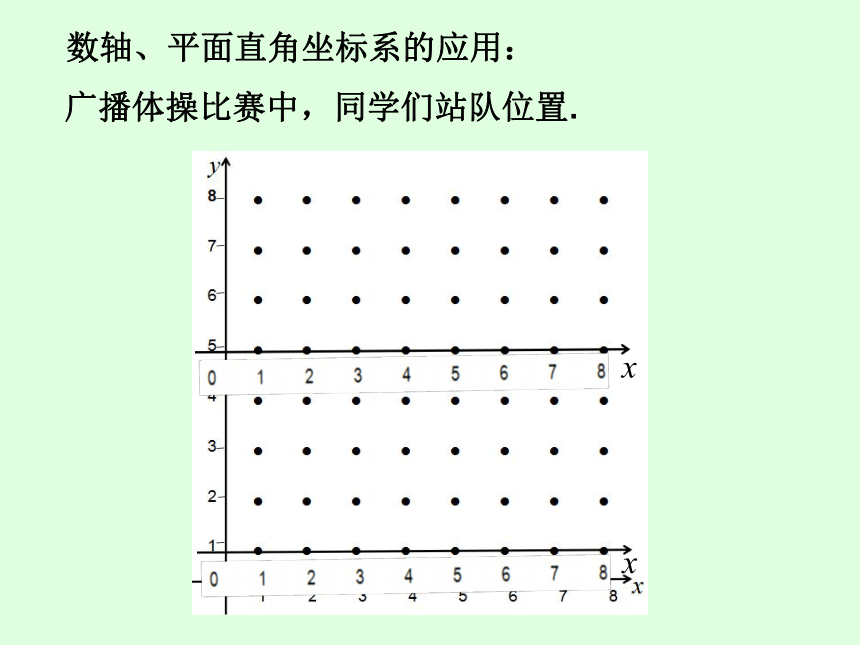
数轴、平面直角坐标系的应用:
广播体操比赛中,同学们站队位置.
x
x
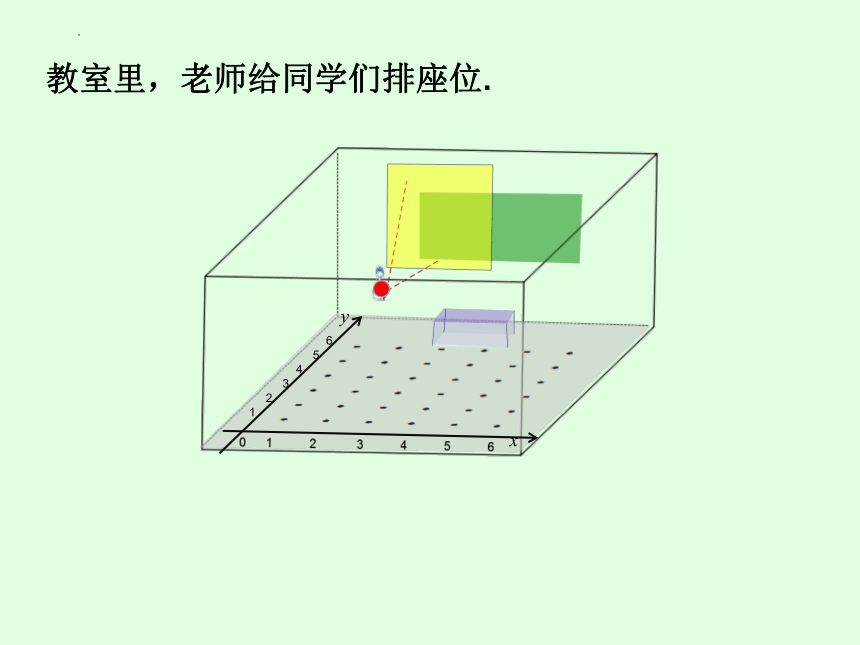
教室里,老师给同学们排座位.
6
5
4
3
2
1
0 1 2 3 4 5 6
y
x
z
A
B
C
O
y
x
z
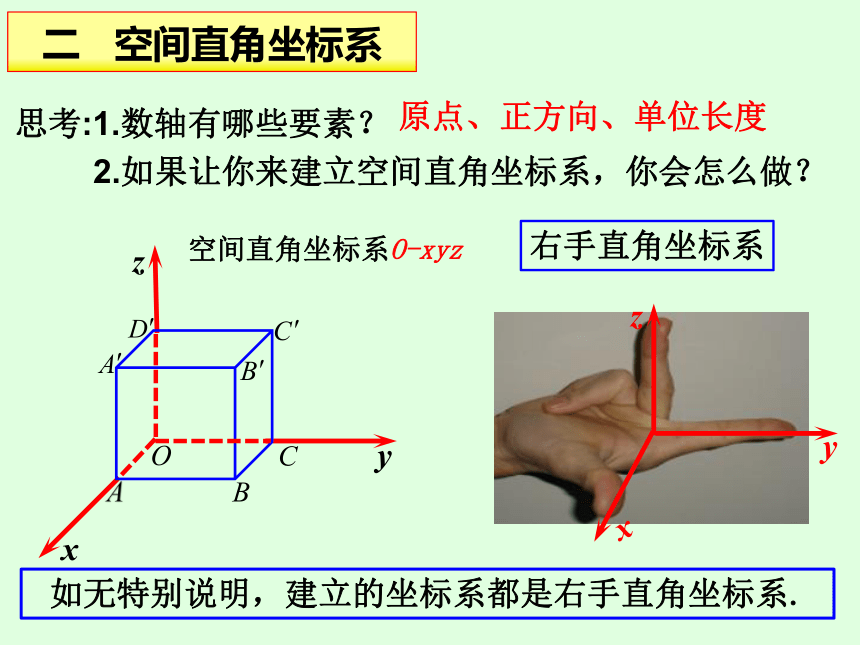
如无特别说明,建立的坐标系都是右手直角坐标系.
二 空间直角坐标系
右手直角坐标系
思考:1.数轴有哪些要素?
2.如果让你来建立空间直角坐标系,你会怎么做?
原点、正方向、单位长度
空间直角坐标系O-xyz
Ⅱ
Ⅶ
平面
Ⅴ
Ⅵ
Ⅰ
平面
平面
Ⅲ
Ⅳ
Ⅷ
O
三个坐标平面、八个卦限
空间直角坐标系的划分
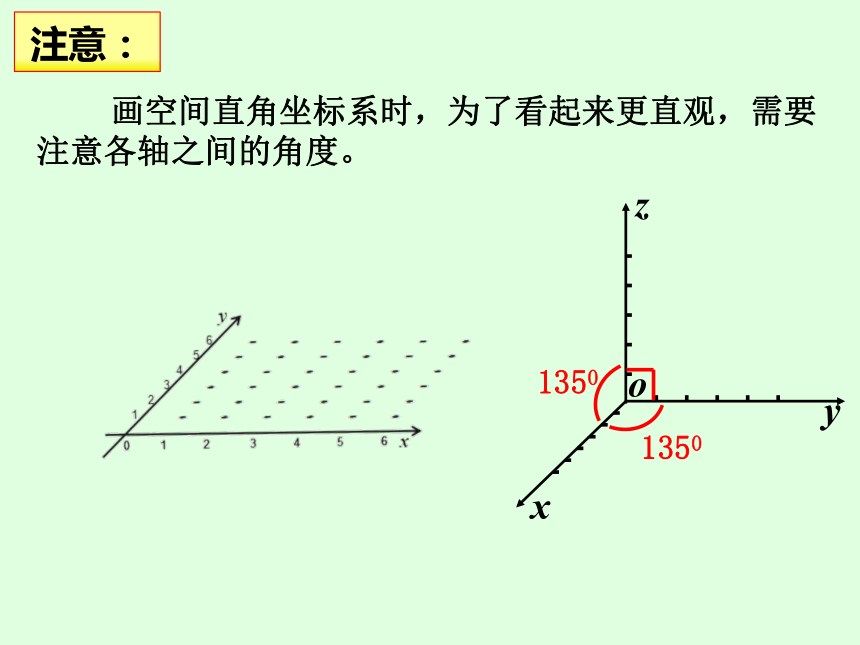
画空间直角坐标系时,为了看起来更直观,需要注意各轴之间的角度。
o
x
y
z
1350
1350
注意:
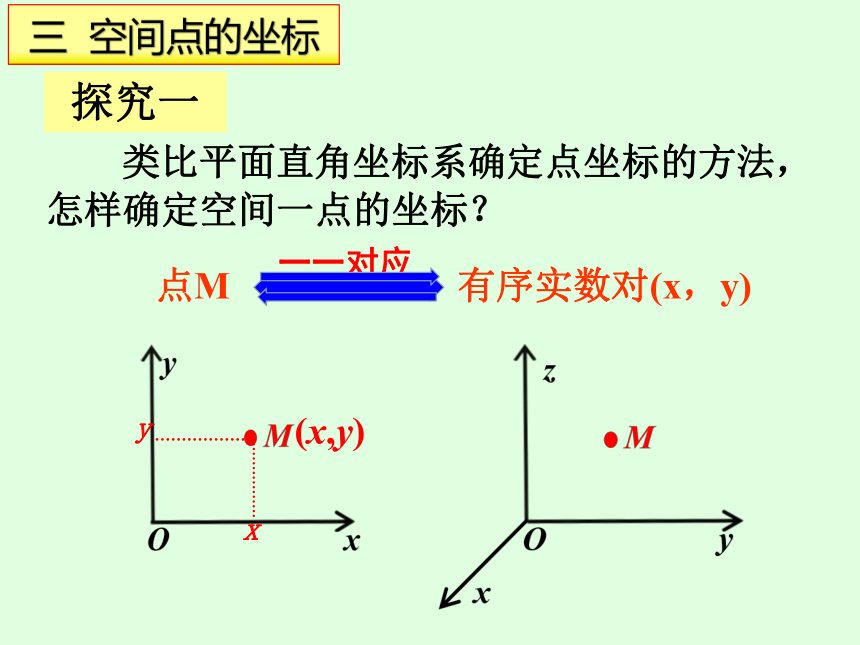
三 空间点的坐标
类比平面直角坐标系确定点坐标的方法,怎样确定空间一点的坐标?
探究一
(x,y)
x
y
点M
一一对应
有序实数对(x,y)
三 空间点的坐标
z
M
O
M
R
Q
P
(x,y,z)
x
y
z
y
x
M
M
x
y
z
z
O
R
Q
P
y
x
(x,y,z)
点M
一一对应
有序实数组(x,y,z)
?
空间一点M的坐标用有序实数组(x,y,z)表示,记作M(x,y,z).其中
x叫做点M的横坐标,
y叫做点M的纵坐标,
z叫做点M的竖坐标.
(0,0,0)
(1,0,0)
(1,1,0)
(0,1,0)
(1,0,1)
(1,1,1)
(0,1,1)
(0,0,1)
y
x
z
A
B
C
O
OABC—A B C D 是单位正方体.确定正方体各个顶点的坐标.
现学现用
(0,0,0)
(1,0,0)
(1,1,0)
(0,1,0)
(1,0,1)
(1,1,1)
(0,1,1)
(0,0,1)
y
x
z
A
B
C
O
现学现用
OABC—A B C D 是单位正方体.确定正方体各个顶点的坐标.
(0,0,0)
(1,0,0)
(1,1,0)
(0,1,0)
(1,0,1)
(1,1,1)
(0,1,1)
(0,0,1)
y
x
z
A
B
C
O
现学现用
思考:怎么确定点(1,1,2),(1,1,-2)位置?
(1,1,-2)
(1,1,2)
OABC—A B C D 是单位正方体.确定正方体各个顶点的坐标.
(0,0,0)
(1,0,0)
(1,1,0)
(0,1,0)
(1,0,1)
(1,1,1)
(0,1,1)
(0,0,1)
y
x
z
A
B
C
O
点的位置 X轴上A Y轴上C Z轴上D 原点O
坐标形式 (1,0,0) (0,1,0) (0,0,1) (0,0,0)
点的位置 XOY面内B YOZ面内C ZOX面内A 不在任一坐标平面内B
坐标形式 (1,1,0) (0,1,1) (1,0,1) (1,1,1)
将各点填入下列表
格后,找一找规律?
找一找
除原点以外的特殊位置
点的位置 X轴上 Y轴上 Z轴上 原点O
坐标形式 (x,0,0) (0,y,0) (0,0,z) (0,0,0)
点的位置 XOY平面内 YOZ平面内 ZOX平面内 不在任一坐标平面内
坐标形式 (x,y,0) (0,y,z) (x,0,z) (x,y,z)
找规律:
O
y
x
z
A
C
B
解: D'(0,0,2)
C (0,4,0)
A'(3,0,2)
B'(3,4,2)
3
4
2
四 学以致用(一)
1、若将教室内的投影仪看成一个点,测得教室前后墙面距离为9,投影仪到前墙面距离为4,到地面距离为2.5,到左墙面距离为2.9。请建立适当的空间直角坐标系,并确定投影仪所在点的坐标。(单位:m)
y
x
z
O
R
Q
P
2.9
4
2.5
(4,2.9,2.5)
方法一:
变式训练
y
x
z
O
Q
P
2.9
-5
2.5
(-5,2.9,2.5)
R
方法二:
变式训练
1、若将教室内的投影仪看成一个点,测得教室前后墙面距离为9,投影仪到前墙面距离为4,到地面距离为2.5,到左墙面距离为2.9。请建立适当的空间直角坐标系,并确定投影仪所在点的坐标。(单位:m)
蚂蚁爬行路线:走直线、转直角
(4,2.9,2.5)
方法一:
y
x
z
O
R
Q
P
2.9
4
2.5
方法二:
(-5,2.9,2.5)
y
x
z
O
Q
P
2.9
-5
2.5
R
M
M
2、在空间直角坐标系中标出下列各点:
A(0,2,4) B(1,0,5) C(0,2,0) D(1,3,4)
o
x
y
z
1
2
3
4
5
1 2 3 4 5
5
4
3
2
1
A(0,2,4)
B(1,0,5)
C(0,2,0)
D(1,3,4)
(1,3,0)
变式训练
x
y
z
O
学以致用(二)
解:把图中的钠原子分成上、中、下三层来写它们所在位置的坐标.
下层坐标分别是
中层坐标分别是
上层坐标分别是
x
y
z
O
五 知识迁移 课后探究
类比平面直角坐标系中关于坐标轴、原点对称的点的关系,空间的点有哪些对称关系?
本 节 收 获
数学思想:类比
课 后 作 业
1.设x,y为任意实数,则所有点P(x,y,3) 构成的集合为______.
2.已知集合A={(x,y,z)|y=0,z=0},集合B={(x,y,z)|x=0,y=0},集合C={(x,y,z)|x=0,z=0},则A∩B∩C=________.
※3.点P(-1,2,3)关于xOy平面对称的点的坐标是( )
A.(1,2,3) B.(-1,-2,3) C.(-1,2,-3) D.(1,-2,-3)
※4.将教室里的投影仪(或电风扇中心)看成一个点,建立适当的空间直角坐标系,确定其坐标,看看你与同桌建系是否一样,坐标又是否一样,并交流心得体会.
谢谢指导!
1.3.1 空间直角坐标系
1.数轴Ox上的点M,怎样表示?
2.直角坐标平面上的点M,怎样表示?
x
O
x
M
x
O
y
M
(x,y)
x
y
我们学了哪些表示点的方法
一 复习导入
数轴、平面直角坐标系的应用:
广播体操比赛中,同学们站队位置.
x
x
教室里,老师给同学们排座位.
6
5
4
3
2
1
0 1 2 3 4 5 6
y
x
z
A
B
C
O
y
x
z
如无特别说明,建立的坐标系都是右手直角坐标系.
二 空间直角坐标系
右手直角坐标系
思考:1.数轴有哪些要素?
2.如果让你来建立空间直角坐标系,你会怎么做?
原点、正方向、单位长度
空间直角坐标系O-xyz
Ⅱ
Ⅶ
平面
Ⅴ
Ⅵ
Ⅰ
平面
平面
Ⅲ
Ⅳ
Ⅷ
O
三个坐标平面、八个卦限
空间直角坐标系的划分
画空间直角坐标系时,为了看起来更直观,需要注意各轴之间的角度。
o
x
y
z
1350
1350
注意:
三 空间点的坐标
类比平面直角坐标系确定点坐标的方法,怎样确定空间一点的坐标?
探究一
(x,y)
x
y
点M
一一对应
有序实数对(x,y)
三 空间点的坐标
z
M
O
M
R
Q
P
(x,y,z)
x
y
z
y
x
M
M
x
y
z
z
O
R
Q
P
y
x
(x,y,z)
点M
一一对应
有序实数组(x,y,z)
?
空间一点M的坐标用有序实数组(x,y,z)表示,记作M(x,y,z).其中
x叫做点M的横坐标,
y叫做点M的纵坐标,
z叫做点M的竖坐标.
(0,0,0)
(1,0,0)
(1,1,0)
(0,1,0)
(1,0,1)
(1,1,1)
(0,1,1)
(0,0,1)
y
x
z
A
B
C
O
OABC—A B C D 是单位正方体.确定正方体各个顶点的坐标.
现学现用
(0,0,0)
(1,0,0)
(1,1,0)
(0,1,0)
(1,0,1)
(1,1,1)
(0,1,1)
(0,0,1)
y
x
z
A
B
C
O
现学现用
OABC—A B C D 是单位正方体.确定正方体各个顶点的坐标.
(0,0,0)
(1,0,0)
(1,1,0)
(0,1,0)
(1,0,1)
(1,1,1)
(0,1,1)
(0,0,1)
y
x
z
A
B
C
O
现学现用
思考:怎么确定点(1,1,2),(1,1,-2)位置?
(1,1,-2)
(1,1,2)
OABC—A B C D 是单位正方体.确定正方体各个顶点的坐标.
(0,0,0)
(1,0,0)
(1,1,0)
(0,1,0)
(1,0,1)
(1,1,1)
(0,1,1)
(0,0,1)
y
x
z
A
B
C
O
点的位置 X轴上A Y轴上C Z轴上D 原点O
坐标形式 (1,0,0) (0,1,0) (0,0,1) (0,0,0)
点的位置 XOY面内B YOZ面内C ZOX面内A 不在任一坐标平面内B
坐标形式 (1,1,0) (0,1,1) (1,0,1) (1,1,1)
将各点填入下列表
格后,找一找规律?
找一找
除原点以外的特殊位置
点的位置 X轴上 Y轴上 Z轴上 原点O
坐标形式 (x,0,0) (0,y,0) (0,0,z) (0,0,0)
点的位置 XOY平面内 YOZ平面内 ZOX平面内 不在任一坐标平面内
坐标形式 (x,y,0) (0,y,z) (x,0,z) (x,y,z)
找规律:
O
y
x
z
A
C
B
解: D'(0,0,2)
C (0,4,0)
A'(3,0,2)
B'(3,4,2)
3
4
2
四 学以致用(一)
1、若将教室内的投影仪看成一个点,测得教室前后墙面距离为9,投影仪到前墙面距离为4,到地面距离为2.5,到左墙面距离为2.9。请建立适当的空间直角坐标系,并确定投影仪所在点的坐标。(单位:m)
y
x
z
O
R
Q
P
2.9
4
2.5
(4,2.9,2.5)
方法一:
变式训练
y
x
z
O
Q
P
2.9
-5
2.5
(-5,2.9,2.5)
R
方法二:
变式训练
1、若将教室内的投影仪看成一个点,测得教室前后墙面距离为9,投影仪到前墙面距离为4,到地面距离为2.5,到左墙面距离为2.9。请建立适当的空间直角坐标系,并确定投影仪所在点的坐标。(单位:m)
蚂蚁爬行路线:走直线、转直角
(4,2.9,2.5)
方法一:
y
x
z
O
R
Q
P
2.9
4
2.5
方法二:
(-5,2.9,2.5)
y
x
z
O
Q
P
2.9
-5
2.5
R
M
M
2、在空间直角坐标系中标出下列各点:
A(0,2,4) B(1,0,5) C(0,2,0) D(1,3,4)
o
x
y
z
1
2
3
4
5
1 2 3 4 5
5
4
3
2
1
A(0,2,4)
B(1,0,5)
C(0,2,0)
D(1,3,4)
(1,3,0)
变式训练
x
y
z
O
学以致用(二)
解:把图中的钠原子分成上、中、下三层来写它们所在位置的坐标.
下层坐标分别是
中层坐标分别是
上层坐标分别是
x
y
z
O
五 知识迁移 课后探究
类比平面直角坐标系中关于坐标轴、原点对称的点的关系,空间的点有哪些对称关系?
本 节 收 获
数学思想:类比
课 后 作 业
1.设x,y为任意实数,则所有点P(x,y,3) 构成的集合为______.
2.已知集合A={(x,y,z)|y=0,z=0},集合B={(x,y,z)|x=0,y=0},集合C={(x,y,z)|x=0,z=0},则A∩B∩C=________.
※3.点P(-1,2,3)关于xOy平面对称的点的坐标是( )
A.(1,2,3) B.(-1,-2,3) C.(-1,2,-3) D.(1,-2,-3)
※4.将教室里的投影仪(或电风扇中心)看成一个点,建立适当的空间直角坐标系,确定其坐标,看看你与同桌建系是否一样,坐标又是否一样,并交流心得体会.
谢谢指导!
