第五章 相交线与平行线模型专题课件 43张PPT 2023--2024学年人教版七年级数学下册
文档属性
| 名称 | 第五章 相交线与平行线模型专题课件 43张PPT 2023--2024学年人教版七年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 22.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-25 00:00:00 | ||
图片预览







文档简介
(共43张PPT)
相交线与平行线
相交线
几条应知应会的重点
1、在同一平面内,过一点有且只有一条直线与已知直线垂直;
或者说过直线外一点有且只有一条直线与已经直线垂直。
2、连接直线外一点与直线上各点的线段中,垂线段最短。
3、直线外一点到这条直线的垂线段的长度,叫点到直线的距离
三线八角
同位角:1和5,2和6,4和8,3和7
内错角:4和6,3和5
同旁内角:4和5,3和6
怎么找这几组角?
首先如果是这三类角一定会有公共边,而且公共边一定是截线,剩下角的两条边是被截线,例如:∠4和∠6公共边是l1,所以l1是截线,∠4的另一条边是l2,∠6的另一条边是l3,所以l2,l3是被截线,在截线(l1)两侧,在被截线(l2,l3)中间,所以是内错角。再比例∠2和∠8,它们没有公共边,所以∠2和∠8不是这三类角。
注意三组角的字面意思:同字指的是在截线同侧,内指的是在两条被截线中间,错指是的被截线两侧(错开)
三线八角
“F”型
“Z”型
“U”型
同位角
内错角
同旁内角
平行线
平行公理:经过直线外一点,有且只有一条直线与这条直线平行。
平行公理推论:如果两条直线都与第三条直线平等,那么这两条直线也互相平行。(可以用来证平行)
平行线判定
1、同位角相等,两直线平行;
2、内错角相等,两直线平行;
3、同旁内角互补,两直线平行。
相交线与平行线
(猪蹄模型)
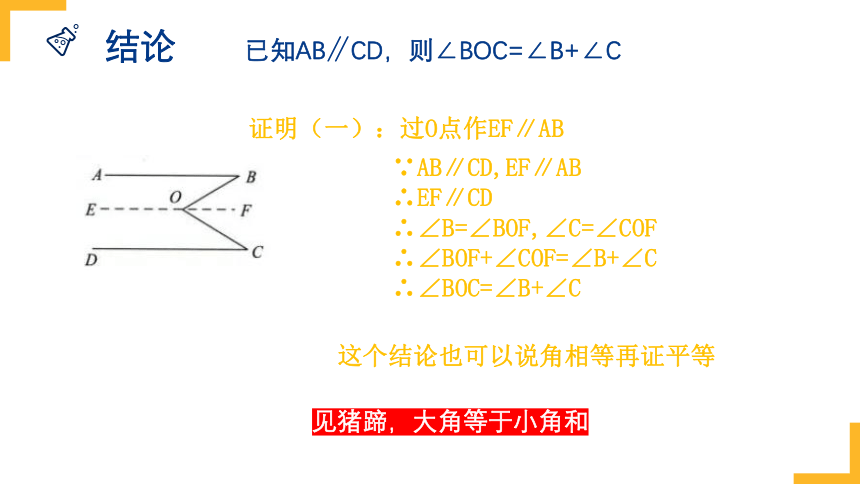
结论
已知AB∥CD,则∠BOC=∠B+∠C
证明(一):过O点作EF∥AB
∵AB∥CD,EF∥AB
∴EF∥CD
∴∠B=∠BOF,∠C=∠COF
∴∠BOF+∠COF=∠B+∠C
∴∠BOC=∠B+∠C
这个结论也可以说角相等再证平等
见猪蹄,大角等于小角和
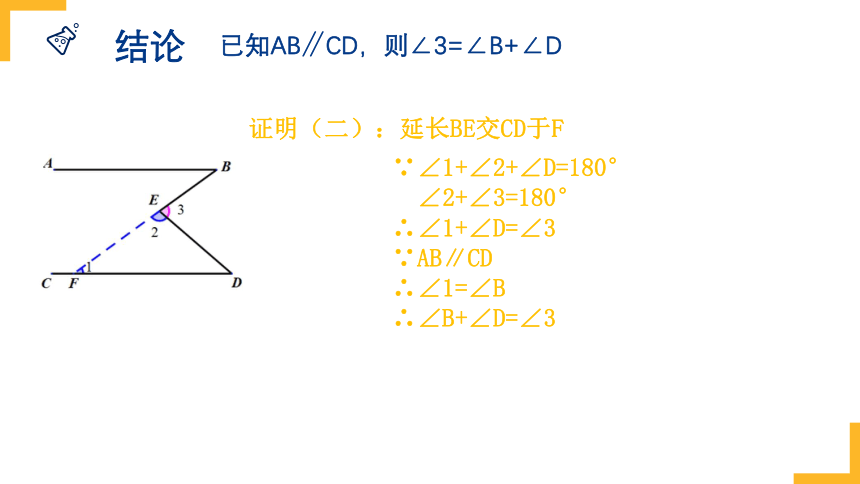
结论
已知AB∥CD,则∠3=∠B+∠D
证明(二):延长BE交CD于F
∵∠1+∠2+∠D=180°
∠2+∠3=180°
∴∠1+∠D=∠3
∵AB∥CD
∴∠1=∠B
∴∠B+∠D=∠3
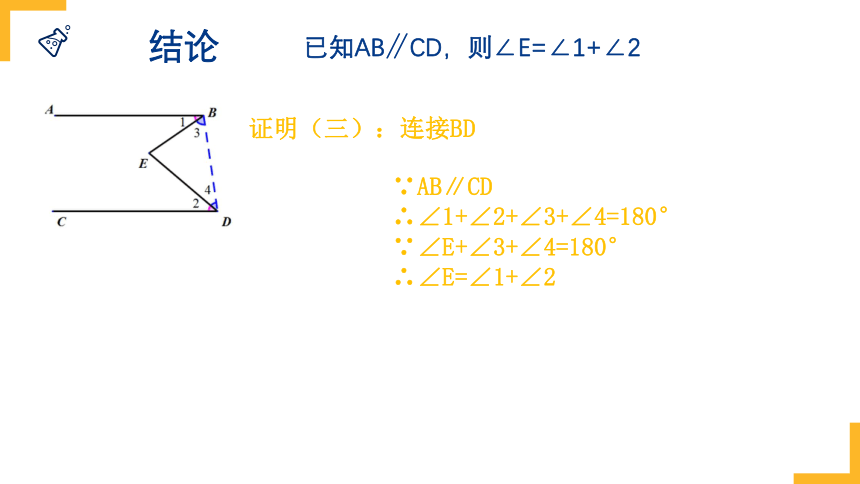
结论
已知AB∥CD,则∠E=∠1+∠2
证明(三):连接BD
∵AB∥CD
∴∠1+∠2+∠3+∠4=180°
∵∠E+∠3+∠4=180°
∴∠E=∠1+∠2
相交线与平行线
(铅笔模型)
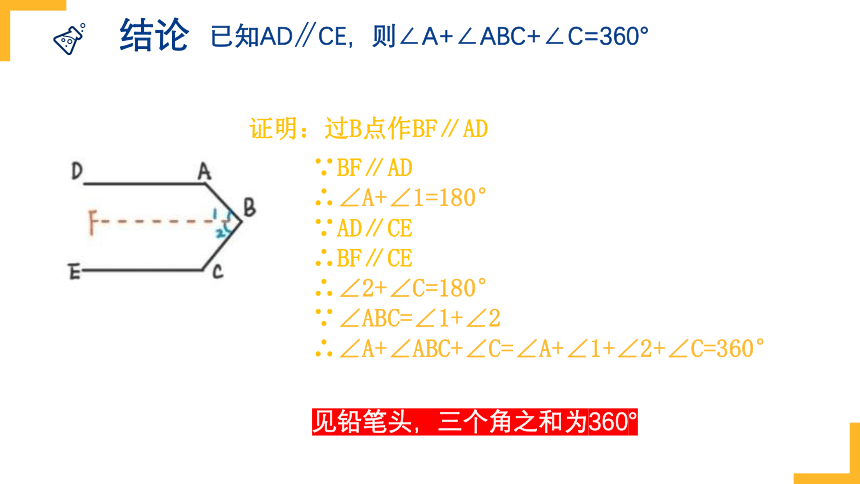
结论
已知AD∥CE,则∠A+∠ABC+∠C=360°
证明:过B点作BF∥AD
∵BF∥AD
∴∠A+∠1=180°
∵AD∥CE
∴BF∥CE
∴∠2+∠C=180°
∵∠ABC=∠1+∠2
∴∠A+∠ABC+∠C=∠A+∠1+∠2+∠C=360°
见铅笔头,三个角之和为360°
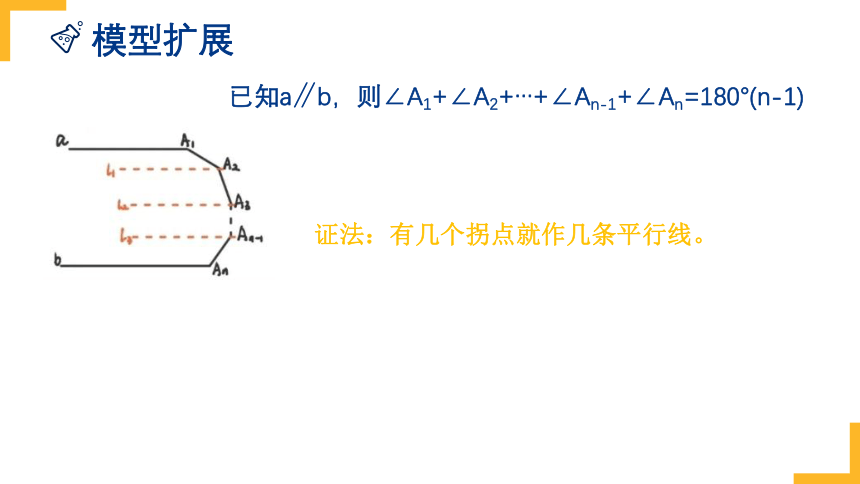
模型扩展
已知a∥b,则∠A1+∠A2+…+∠An-1+∠An=180°(n-1)
证法:有几个拐点就作几条平行线。
相交线与平行线
(锯齿模型)
结论
已知AB∥EF,则∠B+∠D=∠C+∠E
证明:过C点作MN∥AB,过D点作PQ∥AB
∵AB∥EF
∴AB∥MN∥PQ∥EF
∴∠B=∠BCN,∠CDP=∠DCN,∠PDE=∠E
∴∠B+∠CDP+∠PDE=∠BCN+∠DCN+∠E
∴∠B+∠CDE=∠BCD+∠E
见锯齿,朝左边的角的和等于朝右边的角的和
需要注意的是这个模型一定要求∠B和∠E都是锐角
模型变形
已知AB∥EF,则∠C+α=β+γ
证明:延长BA、FE
∵AB∥EF
∴根据锯齿模型的结论,可知:
∠1+γ=∠2+∠C
∵∠1+α=180°,∠2+β=180°
∴(180°-α)+γ=(180°-β)+∠C
即∠C+α=β+γ
模型变换
可以分成一个猪蹄型和一个内错角
可以分成两个猪蹄型
相交线与平行线
(鹰嘴模型)
结论一
已知AD∥CE,则∠ABC=∠A-∠C
证明:过B点作BF∥AD
∵BF∥AD
∴∠ABF+∠A=180°
∵AD∥CE
∴BF∥CE
∴∠FBC+∠C=180°
∴∠FBC+∠C=∠ABF+∠A
∴∠FBC-∠ABF=∠A-∠C
∴∠ABC=∠A-∠C
见鹰嘴,鹰嘴等于大减小
结论二
已知BD∥CE,则∠A=∠C-∠B
证明:∵BD∥CE
∴∠AFD=∠C
∵∠AFD+∠AFB=180°
∠AFB+∠A+∠B=180°
∴∠AFD=∠A+∠B
∴∠C=∠A+∠B,即∠A=∠C-∠B
见鹰嘴,鹰嘴等于大减小
相交线与平行线
(平行平分见等腰模型)
结论一
已知ED∥BC,BD平分∠ABC,则BE=ED
这三个结论只是题设和结论互换了,这说明这个模型里面说了三个事,这三个事只要知道其中两个就可以推出第三个。
结论二
结论三
已知ED∥BC,BE=ED,则BD平分∠ABC
已知BD平分∠ABC,BE=ED,则ED∥BC
结论一解析:
证明:∵ED∥BC
∴∠D=∠1
∵BD平分∠ABC
∴∠2=∠1
∴∠2=∠D
∴BE=ED
其它两个结论证法只是调整一下书写的顺序。
相交线与平行线
(同旁内角双角平分线)
已知AB∥CD,BE平分∠ABD,DE平分∠BDC,过E作AB的垂线FG.
结论:①DE⊥BE;②EF=EG;③BD+BF=DG;④S△BED=
证明:①∵AB∥CD
∴∠ABD+∠BDC=180°
∵BE平分∠ABD,DE平分∠BDC
∴∠EBD=∠ABD,∠EDB=∠BDC
∴∠EBD+∠EDB=∠ABD+∠BDC)
∴∠BED=90°
∴DE⊥BE
证明:②过E点作EH⊥BD于H
∵EH⊥BD,FG⊥AB
∴∠EFB=∠EHB=90°
∵BE平分∠ABD
∴∠EBD=∠EBF
∵BE=BE
∴△EBF≌△EBH
∴EF=EH
H
同理可得
△EDG≌△EDH
∴EG=EH
∴EF=EG
已知AB∥CD,BE平分∠ABD,DE平分∠BDC,过E作AB的垂线FG.
结论:①DE⊥BE;②EF=EG;③DG+BF=BD;④2S△BED=
证明:③由②知:
△EBF≌△EBH,△EDG≌△EDH
∴BF=BH,DH=DG
∴BD=DH+BH=BF+DG
证明:④由②知:
△EBF≌△EBH,△EDG≌△EDH
∴2S△BEH=S四边形FEHB,2S△DEH=S四边形EGDH
∴=S四边形FEHB+S四边形EGDH
=2S△BEH+2S△DEH
=2S△BED
H
针对训练
1、如图,A,B,C三岛的平面图,C岛在A岛的北偏东52°方向,C岛在B岛的北偏西43°方向,则从C岛看A,B两岛的视角∠ACB的度数( )
解析:这个图形逆时针转90°,就是我们上面讲的猪蹄模型。
即:∠ACB=∠A+∠B
针对训练
2、如图,AB∥EF,用α、β、γ的式子表示x
解:延长AB至C
延长之后就成了我们上面讲的锯齿形
∴∠1+β=γ+x
∵∠1=180°-α
∴180°-α+β=γ+x
即x=180°-γ-α+β
C
1
针对训练
分析:这题就是铅笔头模型
180
360
540
720
1620
180(n-1)
3、下列各图中的MA1与NAn平行
(1)图①中的∠A1+∠A2= 度,图②中的∠A1+∠A2+∠A3= 度,图③中的∠A1+∠A2+∠A3+∠A4= 度,图④中的∠A1+∠A2+∠A3+∠A4+∠A5= 度,第⑩个图中∠A1+∠A2+∠A3+…+∠A10= 度
(2)第n个图中的∠A1+∠A2+∠A3+…+∠An= 度
针对训练
(1)由猪蹄模型得:∠E=∠B+∠D
(2)由铅笔模型得:∠E+∠B+∠D=360°
(3)由锯齿模型得:∠B+∠F+∠D=∠E+∠G
4、如图(1)所示是一根木尺折断后的情形,你可能注意过,木尺折断后的断口一般是参差不齐的,那么请你深入考虑一下其中所包含的一类数学问题,我们不妨取名叫“木尺断口问题”
(1)如图(2)所示,已知AB∥CD,请问∠B,∠D,∠E有何关系并说明理由。
(2)如图(3)所示,已知AB∥CD,请问∠B,∠D,∠E有何关系并说明理由。
(3)如图(4)所示,已知AB∥CD,请问∠E+∠G与∠B+∠F+∠D有何关系并说明理由。
针对训练
5、把一副三角板放在水平桌面上,摆放成如图所示的形状,使两个直角顶点重合,两条斜边平行,则∠1的度数是( )
A.90° B.105° C.120° D.135°
B
分析:这题直接用猪蹄就可以了
针对训练
6、如图,在正五边形ABCDE中,AB∥CD,则图中的x的值是 。
85
分析:这题用铅笔模型得
∠D+∠E+∠A=360°
∴x°=360°-150°-125°
∴x=85
针对训练
7、如图,已知∠3=∠1+∠2,
求证:∠A+∠B+∠C+∠D=180°
证明:过点G作HG∥BE
∵HG∥BE
∴∠1=∠EGH
∵∠3=∠1+∠2,∠3=∠EGH+∠FGH
∴∠2=∠FGH
∴HG∥CF
∴BE∥CF
∴∠BMN+∠CNM=180°
∵∠A+∠B=180°-∠BMA=∠BMN
∠C+∠D=180°-∠CND=∠CNA
∴∠A+∠B+∠C+∠D=180°
针对训练
8、如图1,AB∥CD,EF⊥AB于点E,∠AEH=∠FGH=20°,∠H=50°,则∠EFG的度数是( )
A.120° B.130° C.140° D.150°
分析:如图2用猪蹄型,∠H=∠AEH+∠CGH
∵∠AEH=20°,∠H=50°
∴∠CGH=30°
∵∠FGH=20°
∴∠CFG=30°+20°=50°
如图3再用猪蹄型,∠EFG=∠BEF+∠CGF
∵∠BEF=90°
∴∠EFG=90°+50°=140°
C
图1
图3
图2
针对训练
9、如图,AB∥CD,∠ABF=∠ABE,∠CDF=∠CDE,则∠E:∠F=( )
A.2:1 B.3:1 C.3:2 D.4:3
分析:依据猪蹄模型可得
∠F=∠CDF+∠ABF,∠E=∠ABE+∠CDE
∵∠ABF=∠ABE,∠CDF=∠CDE
∴设∠ABE=x,则∠ABF=x
∠CDE=y,则∠CDF=y
∴∠F=x+y=(x+y),∠E=x+y
∴∠F=∠E
∴∠E:∠F=3:2
C
针对训练
10、平面内的两条直线有相交和平行两种位置关系。
(1)如图a,AB∥CD,点P在AB、CD外部,则有∠B=∠BOD,又因∠BOD是△POD的外角,故∠BOD=∠BPD+∠D,得∠BPD=∠B-∠D.将点P移到AB、CD内部,如图b,以上结论是否成立?若成立,说明理由;若不成立,则∠BPD、∠B、∠D之间有何数量关系?请证明你的结论;
(2)在图b中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图c,则∠BPD、∠B、∠D、∠BQD之间有何数量关系?(不需要证明)
(3)根据(2)的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数。
分析:(1)不成立,依据猪蹄模型 ∠BPD=∠B+∠D
(2) 延长BP至E,∠BED=∠BQD+∠B,∠BPD=∠BED+∠D
∴∠BPD=∠BQD+∠B+∠D
这问实际是飞镖模型,会在飞镖模型里重点讲。
(3)可以把原图分成下面两个图,即一个飞镖模型,一个四边形,由飞镖模型得:∠FOE=∠B+∠E+∠F,
由四边形内角和得:∠A+∠C+∠D+∠AOD=360°
∵∠FOE=∠AOD
∴∠A+∠B+∠C+∠D+∠E+∠F=360°
E
O
O
O
针对训练
120°
∠1+∠3=∠2+∠4
∠1+∠3+…+∠2n-1=∠2+∠4+…+∠2n
这题用猪蹄模型和锯齿模型解,具体方法看前面的模型解析。
11、阅读下列材料,并解答下列问题,如图1,AB∥CD,EO和FO交于O,过点O作AB的平行线,我们可以得出∠2与∠1,∠3之间的数量关系是∠2=∠1+∠3.
(1)如图2,直线l1∥l2,AB⊥l1,垂足为O,BC与l2相交于点E,若∠1=30°,则∠B= .
(2)如图3,AB∥CD,则∠1,∠2,∠3,∠4之间的数量关系是什么?并说明理由.
(3)如图4,AB∥CD,图中∠1,∠2,∠3,…,∠2n-1,∠2n之间有什么关系?(直接写出答案)
针对训练
12、如图,在△ABC中OB与OC分别平分∠ABC和∠ACB,过O作DE∥BC,分别交AB、AC于点D、E,若BD+CE=5,则线段DE的长为多少?
分析:由平行平分见等腰模型,可得
△BDO与△ECO都是等腰三角形
∴BD=OD,EO=EC
∴DE=DO+EO=BD+CE
∵BD+CE=5
∴DE=5
针对训练
13、如图,矩形纸片ABCD,其中AD=8,AB=6,沿对角线BD对折,点C在点C′的位置上,BC′交AD于点G.
求证:AG=C′G;
分析:这里面有个红颜色“8”字模型(会在后面的课里单独讲)
∵对折∴∠C′BD=CBD,BC=BC′
∵矩形∴AD∥BC,AD=BC
∴AD=BC′
所以依据平行平分是等腰模型得到△BGD是等腰三角形
∴BG=DG
∴AG=GC′
针对训练
14、如图,在平行四边形ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,及交AD于点E,AB=6,EF=2,则BC长为多少?
分析: ∵ABCD是平行四边形
∴AD∥BC,BC=AD,AB=CD
∵AB=6
∴CD=6
∵BF平分∠ABC,CE平分∠BCD
所以依据平行平分是等腰模型得到△ABF和△DCE都是等腰三角形
∴AB=AF,DE=DC
∴AF=DE=6
∵EF=2
∴BC=AD=AF+DE-EF=6+6-2=10
针对训练
15、已知AB∥DC,点P为平面上一点,连接AP与CP.
(1)如图1,点P在直线AB、CD之间,当∠BAP=60°,∠DCP=20°时,求∠APC.
(2)如图2,点P与直线AB、CD之间,∠BAP与∠DCP的角平分线相交于点K,写出∠AKC与∠APC之间的数量关系,并说明理由.
(3)如图3,点P落在CD外,∠BAP与∠DCP的角平分线相交于点K,∠AKC与∠APC有何数量关系?并说明理由.
解析:(1)由猪蹄模型可得∠P=∠BAP+∠DCP=80°
(2)由猪蹄模型可得∠P=∠BAP+∠DCP
∠K=∠BAK+∠DCK
∵AK、CK为角平分线
∴∠BAP=2∠BAK,∠DCP=2∠DCK
∴∠P=2∠K
(3)由鹰嘴模型可得∠P=∠BAP-∠DCP
∠K=∠BAK-∠DCK
∵AK、CK为角平分线
∴∠BAP=2∠BAK,∠DCP=2∠DCK
∴∠P=2∠K
针对训练
不用解释,猪蹄模型
70°
∠BED=∠AEC=∠A+∠C=36°+54°=90°∵EF平分∠BED,∴∠BEF=∠BED=45°
16、同学们,观察小猪的猪蹄,你会发现一个熟悉的几何图形,我们就把这个图形的形象称为“猪蹄模型”,猪蹄模型中蕴含着的数量关系.
(1)如图1,AB∥CD,E为AB、CE之间一点,连接AE、CE,若∠A=42°,∠C=28°,则∠AEC= .
(2)如图2,AB∥CD,线段AD与线段BC交于点E,∠A=36°,∠C=54°,EF平分∠BED,求∠BEF的度数.
(3)如图3,AB∥CD,线段AD与线段BC交于点G,∠BCD=56°,∠GDE=20°,过点D作DF∥CB交直线AB于点F,AE平分∠BAD,DG平分∠CDF,求∠AED的度数。
针对训练
图4
分析:∵BC∥DF
∴∠BCD+∠CDF=180°,∠CED=∠EDF
∵∠BCD=56°
∴∠CDF=180°-56°=124°
∵DG平分∠CDF
∴∠GDC=∠GDF=∠CDF=62°
∵∠GDE=20°
∴∠CED=∠EDF=62°-20°=42°
∵AB∥CD
∴∠BAD=∠GDC=62°
∵AE平分∠BAD
∴∠BAE=∠BAD=31°
由图4中的模型可得
∠AEC=∠BAE+∠BCD=31°+56°=87°
∴∠AED=∠AEC+∠CED=87°+42°=129°
16、同学们,观察小猪的猪蹄,你会发现一个熟悉的几何图形,我们就把这个图形的形象称为“猪蹄模型”,猪蹄模型中蕴含着的数量关系.
(3)如图3,AB∥CD,线段AD与线段BC交于点G,∠BCD=56°,∠GDE=20°,过点D作DF∥CB交直线AB于点F,AE平分∠BAD,DG平分∠CDF,求∠AED的度数。
你学到了什么?
1、线段双中点模型;
2、拓展到线段三中点;
3、分清线段、射线、直线;
4、双中点中的动点问题;
谢谢观看
相交线与平行线
相交线
几条应知应会的重点
1、在同一平面内,过一点有且只有一条直线与已知直线垂直;
或者说过直线外一点有且只有一条直线与已经直线垂直。
2、连接直线外一点与直线上各点的线段中,垂线段最短。
3、直线外一点到这条直线的垂线段的长度,叫点到直线的距离
三线八角
同位角:1和5,2和6,4和8,3和7
内错角:4和6,3和5
同旁内角:4和5,3和6
怎么找这几组角?
首先如果是这三类角一定会有公共边,而且公共边一定是截线,剩下角的两条边是被截线,例如:∠4和∠6公共边是l1,所以l1是截线,∠4的另一条边是l2,∠6的另一条边是l3,所以l2,l3是被截线,在截线(l1)两侧,在被截线(l2,l3)中间,所以是内错角。再比例∠2和∠8,它们没有公共边,所以∠2和∠8不是这三类角。
注意三组角的字面意思:同字指的是在截线同侧,内指的是在两条被截线中间,错指是的被截线两侧(错开)
三线八角
“F”型
“Z”型
“U”型
同位角
内错角
同旁内角
平行线
平行公理:经过直线外一点,有且只有一条直线与这条直线平行。
平行公理推论:如果两条直线都与第三条直线平等,那么这两条直线也互相平行。(可以用来证平行)
平行线判定
1、同位角相等,两直线平行;
2、内错角相等,两直线平行;
3、同旁内角互补,两直线平行。
相交线与平行线
(猪蹄模型)
结论
已知AB∥CD,则∠BOC=∠B+∠C
证明(一):过O点作EF∥AB
∵AB∥CD,EF∥AB
∴EF∥CD
∴∠B=∠BOF,∠C=∠COF
∴∠BOF+∠COF=∠B+∠C
∴∠BOC=∠B+∠C
这个结论也可以说角相等再证平等
见猪蹄,大角等于小角和
结论
已知AB∥CD,则∠3=∠B+∠D
证明(二):延长BE交CD于F
∵∠1+∠2+∠D=180°
∠2+∠3=180°
∴∠1+∠D=∠3
∵AB∥CD
∴∠1=∠B
∴∠B+∠D=∠3
结论
已知AB∥CD,则∠E=∠1+∠2
证明(三):连接BD
∵AB∥CD
∴∠1+∠2+∠3+∠4=180°
∵∠E+∠3+∠4=180°
∴∠E=∠1+∠2
相交线与平行线
(铅笔模型)
结论
已知AD∥CE,则∠A+∠ABC+∠C=360°
证明:过B点作BF∥AD
∵BF∥AD
∴∠A+∠1=180°
∵AD∥CE
∴BF∥CE
∴∠2+∠C=180°
∵∠ABC=∠1+∠2
∴∠A+∠ABC+∠C=∠A+∠1+∠2+∠C=360°
见铅笔头,三个角之和为360°
模型扩展
已知a∥b,则∠A1+∠A2+…+∠An-1+∠An=180°(n-1)
证法:有几个拐点就作几条平行线。
相交线与平行线
(锯齿模型)
结论
已知AB∥EF,则∠B+∠D=∠C+∠E
证明:过C点作MN∥AB,过D点作PQ∥AB
∵AB∥EF
∴AB∥MN∥PQ∥EF
∴∠B=∠BCN,∠CDP=∠DCN,∠PDE=∠E
∴∠B+∠CDP+∠PDE=∠BCN+∠DCN+∠E
∴∠B+∠CDE=∠BCD+∠E
见锯齿,朝左边的角的和等于朝右边的角的和
需要注意的是这个模型一定要求∠B和∠E都是锐角
模型变形
已知AB∥EF,则∠C+α=β+γ
证明:延长BA、FE
∵AB∥EF
∴根据锯齿模型的结论,可知:
∠1+γ=∠2+∠C
∵∠1+α=180°,∠2+β=180°
∴(180°-α)+γ=(180°-β)+∠C
即∠C+α=β+γ
模型变换
可以分成一个猪蹄型和一个内错角
可以分成两个猪蹄型
相交线与平行线
(鹰嘴模型)
结论一
已知AD∥CE,则∠ABC=∠A-∠C
证明:过B点作BF∥AD
∵BF∥AD
∴∠ABF+∠A=180°
∵AD∥CE
∴BF∥CE
∴∠FBC+∠C=180°
∴∠FBC+∠C=∠ABF+∠A
∴∠FBC-∠ABF=∠A-∠C
∴∠ABC=∠A-∠C
见鹰嘴,鹰嘴等于大减小
结论二
已知BD∥CE,则∠A=∠C-∠B
证明:∵BD∥CE
∴∠AFD=∠C
∵∠AFD+∠AFB=180°
∠AFB+∠A+∠B=180°
∴∠AFD=∠A+∠B
∴∠C=∠A+∠B,即∠A=∠C-∠B
见鹰嘴,鹰嘴等于大减小
相交线与平行线
(平行平分见等腰模型)
结论一
已知ED∥BC,BD平分∠ABC,则BE=ED
这三个结论只是题设和结论互换了,这说明这个模型里面说了三个事,这三个事只要知道其中两个就可以推出第三个。
结论二
结论三
已知ED∥BC,BE=ED,则BD平分∠ABC
已知BD平分∠ABC,BE=ED,则ED∥BC
结论一解析:
证明:∵ED∥BC
∴∠D=∠1
∵BD平分∠ABC
∴∠2=∠1
∴∠2=∠D
∴BE=ED
其它两个结论证法只是调整一下书写的顺序。
相交线与平行线
(同旁内角双角平分线)
已知AB∥CD,BE平分∠ABD,DE平分∠BDC,过E作AB的垂线FG.
结论:①DE⊥BE;②EF=EG;③BD+BF=DG;④S△BED=
证明:①∵AB∥CD
∴∠ABD+∠BDC=180°
∵BE平分∠ABD,DE平分∠BDC
∴∠EBD=∠ABD,∠EDB=∠BDC
∴∠EBD+∠EDB=∠ABD+∠BDC)
∴∠BED=90°
∴DE⊥BE
证明:②过E点作EH⊥BD于H
∵EH⊥BD,FG⊥AB
∴∠EFB=∠EHB=90°
∵BE平分∠ABD
∴∠EBD=∠EBF
∵BE=BE
∴△EBF≌△EBH
∴EF=EH
H
同理可得
△EDG≌△EDH
∴EG=EH
∴EF=EG
已知AB∥CD,BE平分∠ABD,DE平分∠BDC,过E作AB的垂线FG.
结论:①DE⊥BE;②EF=EG;③DG+BF=BD;④2S△BED=
证明:③由②知:
△EBF≌△EBH,△EDG≌△EDH
∴BF=BH,DH=DG
∴BD=DH+BH=BF+DG
证明:④由②知:
△EBF≌△EBH,△EDG≌△EDH
∴2S△BEH=S四边形FEHB,2S△DEH=S四边形EGDH
∴=S四边形FEHB+S四边形EGDH
=2S△BEH+2S△DEH
=2S△BED
H
针对训练
1、如图,A,B,C三岛的平面图,C岛在A岛的北偏东52°方向,C岛在B岛的北偏西43°方向,则从C岛看A,B两岛的视角∠ACB的度数( )
解析:这个图形逆时针转90°,就是我们上面讲的猪蹄模型。
即:∠ACB=∠A+∠B
针对训练
2、如图,AB∥EF,用α、β、γ的式子表示x
解:延长AB至C
延长之后就成了我们上面讲的锯齿形
∴∠1+β=γ+x
∵∠1=180°-α
∴180°-α+β=γ+x
即x=180°-γ-α+β
C
1
针对训练
分析:这题就是铅笔头模型
180
360
540
720
1620
180(n-1)
3、下列各图中的MA1与NAn平行
(1)图①中的∠A1+∠A2= 度,图②中的∠A1+∠A2+∠A3= 度,图③中的∠A1+∠A2+∠A3+∠A4= 度,图④中的∠A1+∠A2+∠A3+∠A4+∠A5= 度,第⑩个图中∠A1+∠A2+∠A3+…+∠A10= 度
(2)第n个图中的∠A1+∠A2+∠A3+…+∠An= 度
针对训练
(1)由猪蹄模型得:∠E=∠B+∠D
(2)由铅笔模型得:∠E+∠B+∠D=360°
(3)由锯齿模型得:∠B+∠F+∠D=∠E+∠G
4、如图(1)所示是一根木尺折断后的情形,你可能注意过,木尺折断后的断口一般是参差不齐的,那么请你深入考虑一下其中所包含的一类数学问题,我们不妨取名叫“木尺断口问题”
(1)如图(2)所示,已知AB∥CD,请问∠B,∠D,∠E有何关系并说明理由。
(2)如图(3)所示,已知AB∥CD,请问∠B,∠D,∠E有何关系并说明理由。
(3)如图(4)所示,已知AB∥CD,请问∠E+∠G与∠B+∠F+∠D有何关系并说明理由。
针对训练
5、把一副三角板放在水平桌面上,摆放成如图所示的形状,使两个直角顶点重合,两条斜边平行,则∠1的度数是( )
A.90° B.105° C.120° D.135°
B
分析:这题直接用猪蹄就可以了
针对训练
6、如图,在正五边形ABCDE中,AB∥CD,则图中的x的值是 。
85
分析:这题用铅笔模型得
∠D+∠E+∠A=360°
∴x°=360°-150°-125°
∴x=85
针对训练
7、如图,已知∠3=∠1+∠2,
求证:∠A+∠B+∠C+∠D=180°
证明:过点G作HG∥BE
∵HG∥BE
∴∠1=∠EGH
∵∠3=∠1+∠2,∠3=∠EGH+∠FGH
∴∠2=∠FGH
∴HG∥CF
∴BE∥CF
∴∠BMN+∠CNM=180°
∵∠A+∠B=180°-∠BMA=∠BMN
∠C+∠D=180°-∠CND=∠CNA
∴∠A+∠B+∠C+∠D=180°
针对训练
8、如图1,AB∥CD,EF⊥AB于点E,∠AEH=∠FGH=20°,∠H=50°,则∠EFG的度数是( )
A.120° B.130° C.140° D.150°
分析:如图2用猪蹄型,∠H=∠AEH+∠CGH
∵∠AEH=20°,∠H=50°
∴∠CGH=30°
∵∠FGH=20°
∴∠CFG=30°+20°=50°
如图3再用猪蹄型,∠EFG=∠BEF+∠CGF
∵∠BEF=90°
∴∠EFG=90°+50°=140°
C
图1
图3
图2
针对训练
9、如图,AB∥CD,∠ABF=∠ABE,∠CDF=∠CDE,则∠E:∠F=( )
A.2:1 B.3:1 C.3:2 D.4:3
分析:依据猪蹄模型可得
∠F=∠CDF+∠ABF,∠E=∠ABE+∠CDE
∵∠ABF=∠ABE,∠CDF=∠CDE
∴设∠ABE=x,则∠ABF=x
∠CDE=y,则∠CDF=y
∴∠F=x+y=(x+y),∠E=x+y
∴∠F=∠E
∴∠E:∠F=3:2
C
针对训练
10、平面内的两条直线有相交和平行两种位置关系。
(1)如图a,AB∥CD,点P在AB、CD外部,则有∠B=∠BOD,又因∠BOD是△POD的外角,故∠BOD=∠BPD+∠D,得∠BPD=∠B-∠D.将点P移到AB、CD内部,如图b,以上结论是否成立?若成立,说明理由;若不成立,则∠BPD、∠B、∠D之间有何数量关系?请证明你的结论;
(2)在图b中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图c,则∠BPD、∠B、∠D、∠BQD之间有何数量关系?(不需要证明)
(3)根据(2)的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数。
分析:(1)不成立,依据猪蹄模型 ∠BPD=∠B+∠D
(2) 延长BP至E,∠BED=∠BQD+∠B,∠BPD=∠BED+∠D
∴∠BPD=∠BQD+∠B+∠D
这问实际是飞镖模型,会在飞镖模型里重点讲。
(3)可以把原图分成下面两个图,即一个飞镖模型,一个四边形,由飞镖模型得:∠FOE=∠B+∠E+∠F,
由四边形内角和得:∠A+∠C+∠D+∠AOD=360°
∵∠FOE=∠AOD
∴∠A+∠B+∠C+∠D+∠E+∠F=360°
E
O
O
O
针对训练
120°
∠1+∠3=∠2+∠4
∠1+∠3+…+∠2n-1=∠2+∠4+…+∠2n
这题用猪蹄模型和锯齿模型解,具体方法看前面的模型解析。
11、阅读下列材料,并解答下列问题,如图1,AB∥CD,EO和FO交于O,过点O作AB的平行线,我们可以得出∠2与∠1,∠3之间的数量关系是∠2=∠1+∠3.
(1)如图2,直线l1∥l2,AB⊥l1,垂足为O,BC与l2相交于点E,若∠1=30°,则∠B= .
(2)如图3,AB∥CD,则∠1,∠2,∠3,∠4之间的数量关系是什么?并说明理由.
(3)如图4,AB∥CD,图中∠1,∠2,∠3,…,∠2n-1,∠2n之间有什么关系?(直接写出答案)
针对训练
12、如图,在△ABC中OB与OC分别平分∠ABC和∠ACB,过O作DE∥BC,分别交AB、AC于点D、E,若BD+CE=5,则线段DE的长为多少?
分析:由平行平分见等腰模型,可得
△BDO与△ECO都是等腰三角形
∴BD=OD,EO=EC
∴DE=DO+EO=BD+CE
∵BD+CE=5
∴DE=5
针对训练
13、如图,矩形纸片ABCD,其中AD=8,AB=6,沿对角线BD对折,点C在点C′的位置上,BC′交AD于点G.
求证:AG=C′G;
分析:这里面有个红颜色“8”字模型(会在后面的课里单独讲)
∵对折∴∠C′BD=CBD,BC=BC′
∵矩形∴AD∥BC,AD=BC
∴AD=BC′
所以依据平行平分是等腰模型得到△BGD是等腰三角形
∴BG=DG
∴AG=GC′
针对训练
14、如图,在平行四边形ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,及交AD于点E,AB=6,EF=2,则BC长为多少?
分析: ∵ABCD是平行四边形
∴AD∥BC,BC=AD,AB=CD
∵AB=6
∴CD=6
∵BF平分∠ABC,CE平分∠BCD
所以依据平行平分是等腰模型得到△ABF和△DCE都是等腰三角形
∴AB=AF,DE=DC
∴AF=DE=6
∵EF=2
∴BC=AD=AF+DE-EF=6+6-2=10
针对训练
15、已知AB∥DC,点P为平面上一点,连接AP与CP.
(1)如图1,点P在直线AB、CD之间,当∠BAP=60°,∠DCP=20°时,求∠APC.
(2)如图2,点P与直线AB、CD之间,∠BAP与∠DCP的角平分线相交于点K,写出∠AKC与∠APC之间的数量关系,并说明理由.
(3)如图3,点P落在CD外,∠BAP与∠DCP的角平分线相交于点K,∠AKC与∠APC有何数量关系?并说明理由.
解析:(1)由猪蹄模型可得∠P=∠BAP+∠DCP=80°
(2)由猪蹄模型可得∠P=∠BAP+∠DCP
∠K=∠BAK+∠DCK
∵AK、CK为角平分线
∴∠BAP=2∠BAK,∠DCP=2∠DCK
∴∠P=2∠K
(3)由鹰嘴模型可得∠P=∠BAP-∠DCP
∠K=∠BAK-∠DCK
∵AK、CK为角平分线
∴∠BAP=2∠BAK,∠DCP=2∠DCK
∴∠P=2∠K
针对训练
不用解释,猪蹄模型
70°
∠BED=∠AEC=∠A+∠C=36°+54°=90°∵EF平分∠BED,∴∠BEF=∠BED=45°
16、同学们,观察小猪的猪蹄,你会发现一个熟悉的几何图形,我们就把这个图形的形象称为“猪蹄模型”,猪蹄模型中蕴含着的数量关系.
(1)如图1,AB∥CD,E为AB、CE之间一点,连接AE、CE,若∠A=42°,∠C=28°,则∠AEC= .
(2)如图2,AB∥CD,线段AD与线段BC交于点E,∠A=36°,∠C=54°,EF平分∠BED,求∠BEF的度数.
(3)如图3,AB∥CD,线段AD与线段BC交于点G,∠BCD=56°,∠GDE=20°,过点D作DF∥CB交直线AB于点F,AE平分∠BAD,DG平分∠CDF,求∠AED的度数。
针对训练
图4
分析:∵BC∥DF
∴∠BCD+∠CDF=180°,∠CED=∠EDF
∵∠BCD=56°
∴∠CDF=180°-56°=124°
∵DG平分∠CDF
∴∠GDC=∠GDF=∠CDF=62°
∵∠GDE=20°
∴∠CED=∠EDF=62°-20°=42°
∵AB∥CD
∴∠BAD=∠GDC=62°
∵AE平分∠BAD
∴∠BAE=∠BAD=31°
由图4中的模型可得
∠AEC=∠BAE+∠BCD=31°+56°=87°
∴∠AED=∠AEC+∠CED=87°+42°=129°
16、同学们,观察小猪的猪蹄,你会发现一个熟悉的几何图形,我们就把这个图形的形象称为“猪蹄模型”,猪蹄模型中蕴含着的数量关系.
(3)如图3,AB∥CD,线段AD与线段BC交于点G,∠BCD=56°,∠GDE=20°,过点D作DF∥CB交直线AB于点F,AE平分∠BAD,DG平分∠CDF,求∠AED的度数。
你学到了什么?
1、线段双中点模型;
2、拓展到线段三中点;
3、分清线段、射线、直线;
4、双中点中的动点问题;
谢谢观看
