4.1.线段、射线、直线课件 38张PPT 2023-2024学年北师大版数学七年级上册
文档属性
| 名称 | 4.1.线段、射线、直线课件 38张PPT 2023-2024学年北师大版数学七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-25 00:00:00 | ||
图片预览









文档简介
(共38张PPT)
1. 线段、射线、直线
北师大版·七年级上册
第四章 基本平面图形
猜猜看
风筝跑了(打一个数学名词)
线段(断)
1.能结合现实世界中的具体事例说明线段、射线、直线概念的意义以及它们的区别与联系.
2. 能用正确的方法表示直线、射线、线段.
3. 通过实践操作活动,明确“两点确定一条直线”的意义,积累数学活动经验.
素养目标
新课导入
观察欣赏这一组生活中的图片,从中你能找出我们所熟悉的几何图形吗?
新课探究
绷紧的琴弦、黑板的边沿都可以近似地看作线段.
线段有两个端点.
将线段向一个方向无限延长就形成了射线.
手电筒、探照灯所射出的光线可以近似地看做射线. 射线有一个端点.
将线段向两个方向无限延长形成了直线。
直线没有端点。
议一议
生活中有哪些物体可以近似地看做线段、射线、直线?
线段:灯管、桌子的边沿……
射线:把灯泡看成一点、光线射向远方……
直线:笔直的公路、数轴……
请在导学案44页空白处画
一条线段
一条射线
一条直线
想一想:线段、射线、直线如何表示呢?
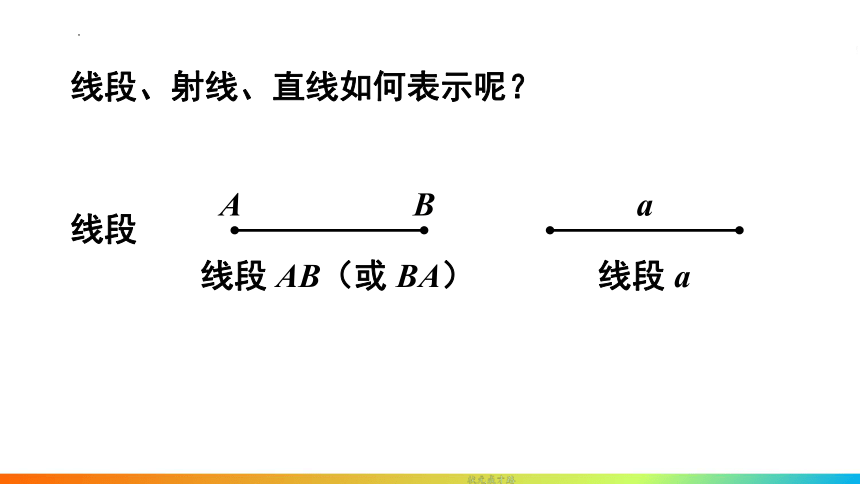
线段、射线、直线如何表示呢?
线段
A
B
线段 AB(或 BA)
线段 a
a
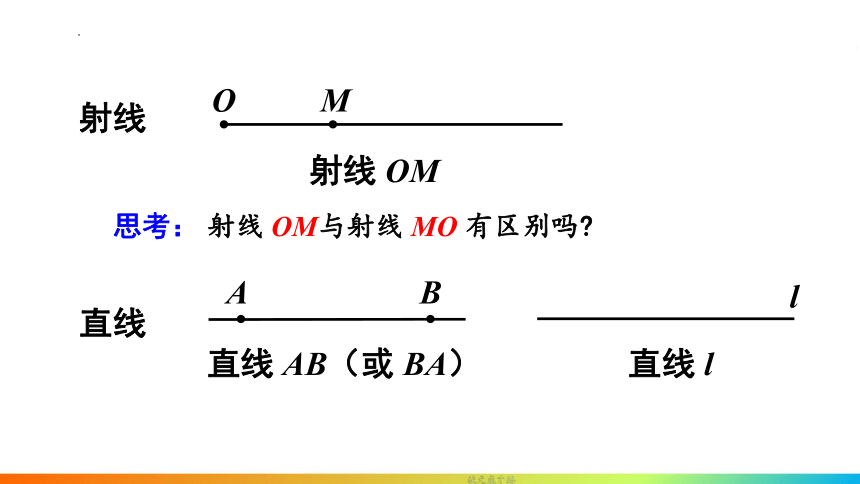
射线
O
M
射线 OM
直线
A
B
直线 AB(或 BA)
l
直线 l
思考: 射线 OM与射线 MO 有区别吗
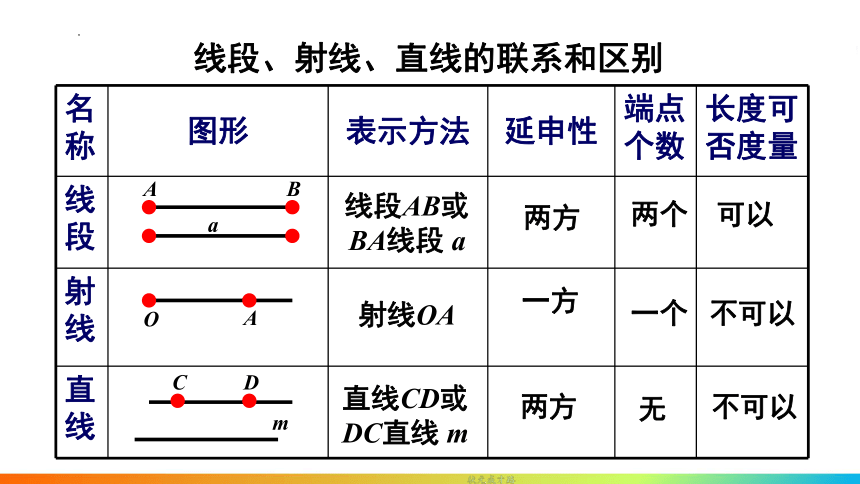
线段、射线、直线的联系和区别
名称 图形 表示方法 延申性 端点个数 长度可否度量
线段
射线
直线
线段AB或BA线段 a
两方
不可以
不可以
可以
两个
一个
一方
无
两方
直线CD或DC直线 m
射线OA
A
B
a
O
A
D
C
m
A
B
A
B
直线、射线、线段三者的联系:
A
B
2. 将线段向两个方向无限延长就形成了直线.
1. 将线段向一个方向无限延长就形成了射线.
3. 线段和射线都是直线的一部分.
讨论 分别画一条直线、射线和线段,议一议它们之间的联系和区别.
探究新知
判断下列语句是否正确:
Ⅰ.一条直线可以表示为“直线 A”.
Ⅱ.一条直线可以表示为“直线 ab”.
Ⅲ.一条直线既可以记为“直线 AB”,又可以记为“直线 BA”,还可以记为“直线 m”.
×
×
判断下列说法是否正确:
a. 线段 AB 与射线 AB 都是直线 AB 的一部分.
b. 直线 AB 与直线 BA 是同一条直线.
c. 射线 AB 与射线 BA 是同一条射线.
d. 端点重合的两条射线一定是同一条射线.
×
×
1.如图,A,B,C三点在一条直线上,
(1) 图中有几条直线,怎样表示它们?
(2) 图中有几条线段,怎样表示它们?
(3) 射线 AB 和射线 AC 是同一条射线吗?
(4) 图中有几条射线?写出以点B为端点的射线.
解:(1) 1条,直线AB或直线AC或直线BC;
(2) 3条,线段AB,线段BC,线段AC;
(3) 是;
(4) 6条.以B为端点的射线有射线BC、射线BA.
A
B
C
能力提升题
课堂检测
做一做
(1)过一点 A 可以画几条直线?
无数条
(2)过两点 A,B 可以画几条直线?
一条
(3)如果你想将一根细木条固定在墙上,至少需要几个钉子?
2个
根据生活经验,我们发现:
经过两点有且只有一条直线.
这一事实可以简述为:两点确定一条直线.
砌墙时常在墙角分别固定一木桩,可以拉一条直的参照线.
做家具时弹墨线.
举生活中关于这一条性质的运用的例子。
射击的时候,你知道是如何瞄准目标的吗?
巩固练习
问题2 观察下图,说一说点和直线有哪些位置关系.
A
B
l
如图,点 A 在直线 l 上,点 B 在直线 l 外,
或者说:直线 l 经过点 A,
点 B 不在直线 l 上 (直线 l 不经过点B ).
探究新知
b
a
问题3 如图,直线a与直线b有什么位置关系?
当两条不同的直线有一个公共点时,我们就称
这两条直线相交,这个公共点叫做它们的交点.
交点
O
直线 a 和 b 相交于点O
探究新知
3、根据语句画图:(1)画直线AB经过点P;(2)点C在线段AB上;(3)线段AB与CD相交于O;
(4)画线段MN与PQ相交于M.
导学案43页
例2 如图,已知平面上三点 A、B、C.
(1) 画线段 AB;
(2) 画直线 BC;
(3) 画射线 CA;
解:(1)、(2)、(3)题解答如图所示.
导学案43页
(4) 如何由线段 AB 得到射线 AB 和直线 AB 呢?
解:将线段 AB 向 AB 方向延伸得到射线 AB,将线段 AB 向两个方向延伸得到直线 AB,如图所示.
解:直线 AB 与直线 BC 有一个公共点,如图所示.
(5)直线 AB 与直线 BC 有几个公共点?
图中直线 AB,射线 CD,线段 MN 其中两个能够相交的是( )
练一练
D
活动1:图中共有几条线段?说明你分析这个问题的具体思路;
合作探究
解析:以 A 为端点的线段有 AB,AC,AD,AE,共 4 条,以 B 为端点且与前面不重复的线段有 BC,BD,BE,共 3 条,以 C 为端点且与前面不重复的线段有CD,CE,共 2 条,以 D 为端点且与前面不重复的线段有DE,共 1 条,从而共有4+3+2+1=10(条)线段.
1. 当直线a上有1个点时,可得到 条射线, 条线段;
·
A
B
O
a
·
·
·
C
2. 当直线a上有2个点时,可得到 条射线, 条线段;
3. 当直线a上有3个点时,可得到 条射线, 条线段;
4. 当直线a上有4个点时,可得到 条射线, 条线段;
活动2:当直线 a 上有 n 个点时,可得到 条射线, 条线段.
2
0
4
1
6
3
8
6
2n
n(n-1)
2
5. 当直线a上有5个点时,可得到 条射线, 条线段;
10
6. 当直线a上有6个点时,可得到 条射线, 条线段;
10
12
15
3. 两条直线相交,最多有 1 个交点.三条直线相交,最多有 3 个交点.四条直线相交,最多有多少个交点?
植树时,要把一排树植整齐,要怎么办?
只要定出两个树坑的位置就能确定同一行的树坑所在的直线.
直线、射线、线段
概念
表示方法
两点确定一条直线
射线 OA;射线b
直线 AB(或直线BA);直线 l
射线OA与射线AO是不同的两条射线
联系与区别
基本事实
绷紧的琴弦、人行横道都可以近似地看做线段
探照灯的灯光给我们以射线的形象
向两个方向无限延伸的铁轨给我们以直线的形象
线段 AB(或线段BA);线段 a
课堂小结
随堂演练
判断下列各题,对的打“√”,错的打“×”。
(1)线段有两个端点,射线有一个端点,直线没有端点。( )
(2)线段 AB 长 2 000 米,射线 AB 长 2 000 米。 ( )
(3)射线比直线短一半。( )
(4)线段,射线可以度量长度,直线不能。( )
(5)射线 AB 与射线 BA 是同一条射线。( )
√
×
×
×
×
往返于A、B两地的客车,中途停靠三个站,每两站间的票价均不相同,问:
(1)有多少种不同的票价?
(2)要准备多少种车票?
解:画出示意图如下:
A
C
D
E
B
(1)图中一共有10条线段,故有10种不同的票价.
(2)来回的车票不同,故有10×2=20(种)不同的车票.
拓广探索题
课堂检测
读一读
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
1. 线段、射线、直线
北师大版·七年级上册
第四章 基本平面图形
猜猜看
风筝跑了(打一个数学名词)
线段(断)
1.能结合现实世界中的具体事例说明线段、射线、直线概念的意义以及它们的区别与联系.
2. 能用正确的方法表示直线、射线、线段.
3. 通过实践操作活动,明确“两点确定一条直线”的意义,积累数学活动经验.
素养目标
新课导入
观察欣赏这一组生活中的图片,从中你能找出我们所熟悉的几何图形吗?
新课探究
绷紧的琴弦、黑板的边沿都可以近似地看作线段.
线段有两个端点.
将线段向一个方向无限延长就形成了射线.
手电筒、探照灯所射出的光线可以近似地看做射线. 射线有一个端点.
将线段向两个方向无限延长形成了直线。
直线没有端点。
议一议
生活中有哪些物体可以近似地看做线段、射线、直线?
线段:灯管、桌子的边沿……
射线:把灯泡看成一点、光线射向远方……
直线:笔直的公路、数轴……
请在导学案44页空白处画
一条线段
一条射线
一条直线
想一想:线段、射线、直线如何表示呢?
线段、射线、直线如何表示呢?
线段
A
B
线段 AB(或 BA)
线段 a
a
射线
O
M
射线 OM
直线
A
B
直线 AB(或 BA)
l
直线 l
思考: 射线 OM与射线 MO 有区别吗
线段、射线、直线的联系和区别
名称 图形 表示方法 延申性 端点个数 长度可否度量
线段
射线
直线
线段AB或BA线段 a
两方
不可以
不可以
可以
两个
一个
一方
无
两方
直线CD或DC直线 m
射线OA
A
B
a
O
A
D
C
m
A
B
A
B
直线、射线、线段三者的联系:
A
B
2. 将线段向两个方向无限延长就形成了直线.
1. 将线段向一个方向无限延长就形成了射线.
3. 线段和射线都是直线的一部分.
讨论 分别画一条直线、射线和线段,议一议它们之间的联系和区别.
探究新知
判断下列语句是否正确:
Ⅰ.一条直线可以表示为“直线 A”.
Ⅱ.一条直线可以表示为“直线 ab”.
Ⅲ.一条直线既可以记为“直线 AB”,又可以记为“直线 BA”,还可以记为“直线 m”.
×
×
判断下列说法是否正确:
a. 线段 AB 与射线 AB 都是直线 AB 的一部分.
b. 直线 AB 与直线 BA 是同一条直线.
c. 射线 AB 与射线 BA 是同一条射线.
d. 端点重合的两条射线一定是同一条射线.
×
×
1.如图,A,B,C三点在一条直线上,
(1) 图中有几条直线,怎样表示它们?
(2) 图中有几条线段,怎样表示它们?
(3) 射线 AB 和射线 AC 是同一条射线吗?
(4) 图中有几条射线?写出以点B为端点的射线.
解:(1) 1条,直线AB或直线AC或直线BC;
(2) 3条,线段AB,线段BC,线段AC;
(3) 是;
(4) 6条.以B为端点的射线有射线BC、射线BA.
A
B
C
能力提升题
课堂检测
做一做
(1)过一点 A 可以画几条直线?
无数条
(2)过两点 A,B 可以画几条直线?
一条
(3)如果你想将一根细木条固定在墙上,至少需要几个钉子?
2个
根据生活经验,我们发现:
经过两点有且只有一条直线.
这一事实可以简述为:两点确定一条直线.
砌墙时常在墙角分别固定一木桩,可以拉一条直的参照线.
做家具时弹墨线.
举生活中关于这一条性质的运用的例子。
射击的时候,你知道是如何瞄准目标的吗?
巩固练习
问题2 观察下图,说一说点和直线有哪些位置关系.
A
B
l
如图,点 A 在直线 l 上,点 B 在直线 l 外,
或者说:直线 l 经过点 A,
点 B 不在直线 l 上 (直线 l 不经过点B ).
探究新知
b
a
问题3 如图,直线a与直线b有什么位置关系?
当两条不同的直线有一个公共点时,我们就称
这两条直线相交,这个公共点叫做它们的交点.
交点
O
直线 a 和 b 相交于点O
探究新知
3、根据语句画图:(1)画直线AB经过点P;(2)点C在线段AB上;(3)线段AB与CD相交于O;
(4)画线段MN与PQ相交于M.
导学案43页
例2 如图,已知平面上三点 A、B、C.
(1) 画线段 AB;
(2) 画直线 BC;
(3) 画射线 CA;
解:(1)、(2)、(3)题解答如图所示.
导学案43页
(4) 如何由线段 AB 得到射线 AB 和直线 AB 呢?
解:将线段 AB 向 AB 方向延伸得到射线 AB,将线段 AB 向两个方向延伸得到直线 AB,如图所示.
解:直线 AB 与直线 BC 有一个公共点,如图所示.
(5)直线 AB 与直线 BC 有几个公共点?
图中直线 AB,射线 CD,线段 MN 其中两个能够相交的是( )
练一练
D
活动1:图中共有几条线段?说明你分析这个问题的具体思路;
合作探究
解析:以 A 为端点的线段有 AB,AC,AD,AE,共 4 条,以 B 为端点且与前面不重复的线段有 BC,BD,BE,共 3 条,以 C 为端点且与前面不重复的线段有CD,CE,共 2 条,以 D 为端点且与前面不重复的线段有DE,共 1 条,从而共有4+3+2+1=10(条)线段.
1. 当直线a上有1个点时,可得到 条射线, 条线段;
·
A
B
O
a
·
·
·
C
2. 当直线a上有2个点时,可得到 条射线, 条线段;
3. 当直线a上有3个点时,可得到 条射线, 条线段;
4. 当直线a上有4个点时,可得到 条射线, 条线段;
活动2:当直线 a 上有 n 个点时,可得到 条射线, 条线段.
2
0
4
1
6
3
8
6
2n
n(n-1)
2
5. 当直线a上有5个点时,可得到 条射线, 条线段;
10
6. 当直线a上有6个点时,可得到 条射线, 条线段;
10
12
15
3. 两条直线相交,最多有 1 个交点.三条直线相交,最多有 3 个交点.四条直线相交,最多有多少个交点?
植树时,要把一排树植整齐,要怎么办?
只要定出两个树坑的位置就能确定同一行的树坑所在的直线.
直线、射线、线段
概念
表示方法
两点确定一条直线
射线 OA;射线b
直线 AB(或直线BA);直线 l
射线OA与射线AO是不同的两条射线
联系与区别
基本事实
绷紧的琴弦、人行横道都可以近似地看做线段
探照灯的灯光给我们以射线的形象
向两个方向无限延伸的铁轨给我们以直线的形象
线段 AB(或线段BA);线段 a
课堂小结
随堂演练
判断下列各题,对的打“√”,错的打“×”。
(1)线段有两个端点,射线有一个端点,直线没有端点。( )
(2)线段 AB 长 2 000 米,射线 AB 长 2 000 米。 ( )
(3)射线比直线短一半。( )
(4)线段,射线可以度量长度,直线不能。( )
(5)射线 AB 与射线 BA 是同一条射线。( )
√
×
×
×
×
往返于A、B两地的客车,中途停靠三个站,每两站间的票价均不相同,问:
(1)有多少种不同的票价?
(2)要准备多少种车票?
解:画出示意图如下:
A
C
D
E
B
(1)图中一共有10条线段,故有10种不同的票价.
(2)来回的车票不同,故有10×2=20(种)不同的车票.
拓广探索题
课堂检测
读一读
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
