吉林省长春市长春新区吉大慧谷学校2023-2024年度上学期第二次质量监测九年级数学试卷(PDF版,无答案)
文档属性
| 名称 | 吉林省长春市长春新区吉大慧谷学校2023-2024年度上学期第二次质量监测九年级数学试卷(PDF版,无答案) |  | |
| 格式 | |||
| 文件大小 | 662.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-24 16:32:52 | ||
图片预览


文档简介
2023-2024 年度上学期长春新区吉大慧谷学校第二次质量监测
九年级数学试卷
考试时间:120分钟 总分:120分 出题人:董丽新 一审:张艳秋 终审:肖静纯
一、选择题(共 8小题,每题 3分,共 24分)
1.抛物线 y=x2+1 的顶点是( )
A.(1,0) B.(0,1) C.(0,﹣1) D.(1,1)
2.如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个
点 A、 B 、C 都在横线上.若线段BC = 3cm,则线段 AC 的长是( )
A.3.5cm B.4cm C.4.5cm D.5cm
3. 2 tan45 的值为( )
1
A.1 B. 2 C.2 D.
2
4.某书店拿取高处书籍的登高梯如图位置摆放,登高梯 AC 的顶端 A 恰好放在书架
的第七层的顶端.已知登高梯的长度 AC 为 3 米,登高梯与地面的夹角 ACB 为
72 ,则书架第七层顶端离地面的高度 AB 为( )
3 3
A.3sin72 米 B. 米 C.3cos72 米 D. 米
sin 72 cos 72
(第 2 题) (第 4 题) (第 5 题) (第 6 题)
5. 如图,△ABC 的顶点 A、B、C 均在⊙O 上,若∠ABC=25°,则∠AOC 的大小是
( )
A.25° B.50° C.65° D.75°
6.如图,在△ABC 中,点D、E、F分别为边BC,AD,CE 的中点,S△ABC = 16cm ,
则 S△EBF =( )
A.8cm2 B. 4cm2 C.6cm2 D. 2cm2
九年级 数学( 共 6 页·第1页)
7.某超市经销一种水果,每千克盈利 10 元,每天销售 500 千克,经市场调查反映:
若每千克涨价 1 元,每天销售量减少 20 千克,设每千克涨价 x(单位:元),且
0 x 25,每天售出商品的利润为y(单位:元),则y与x的函数关系式是( )
A. y = 500 20x B. y = (500 20x)(10+ x)
C. y = (500+10x)(10 x) D. y = (500 10x)(10+ x)
k
8.如图,在平面直角坐标系中,点 A、 B 在函数 y = (k 0, x 0) 的图象上,分别
x
以 A、 B 为圆心,1为半径作圆,当 A与 x轴相切、 B与 y 轴相切时,连结
AB, AB = 4 2 ,则 k 的值为( )
A.3 B. 4 2 C.4 D.5
y
A
B O
A x B
O
(第 8 题) (第 11 题) (第 12 题) (第 13 题)
二、填空题(共 6小题,每题 3分,共 18分)
9.已知 O的半径为5cm,若OP = 6cm,那么点 P 在 O .
10.若一元二次方程 x2-2x-3a=0 无实根,则 a 取值范围是 .
11.如图,△ABC 和△DEF 是以点O为位似中心的位似图形,相似比为 2:3,则
△ABC 和△DEF 的面积比是________.
12.如图,小明用自制的直角三角形纸板 DEF 测量树的高度 AB.他调整自己的位
置,设法使斜边 DF 保持水平,并且边 DE 与点 B 在同一直线上,已知纸板的两
条直角边 DE=40cm.EF=30cm,测得边 DF 离地面的高度 AC=1.5m,CD=
10m,求树高 AB 是________m.
13.正方形网格中, AOB如图放置,则sin AOB的值为________.
14.当 x=a 或 x=b(a≠b)时,代数式 x2-4x+2的值相等,则当 x=a+b 时,代数式
x2-4x+2的值为________.
九年级 数学( 共 6 页·第2页)
三、计算题(共 78分)
2 2
15.(6 分)计算:(1) 3 + 3 + 4cos30° 27 (2) x 3x + 2 = 0
16.(6 分)在一个不透明的布袋里装有 4 个球,其中 1 个红球,1 个黄球,2 个白球,
它们除颜色外其余都相同.
(1)若从中任意摸出一个球,摸出白球的概率为 ;
(2)先摸出 1 个球,记下颜色后不放回,再摸出 1 个球,求两次摸出的球恰好一
黄一白的概率(要求画树状图或列表).(设红球为A,黄球为B,白球为C)
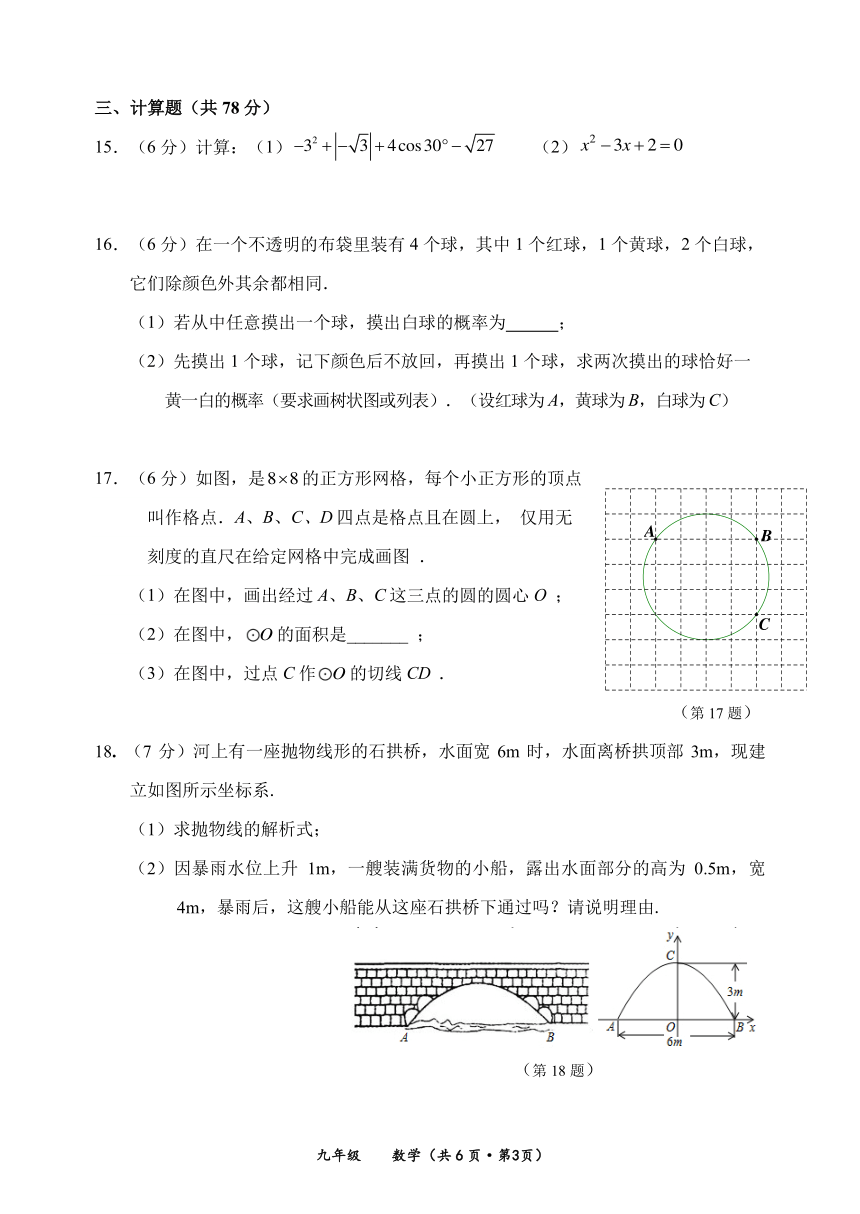
17.(6 分)如图,是8 8的正方形网格,每个小正方形的顶点
叫作格点.A、B、C、D 四点是格点且在圆上, 仅用无
A B A B
刻度的直尺在给定网格中完成画图 .
(1)在图中,画出经过 A、B、C 这三点的圆的圆心 O ;
C D C
(2)在图中, O 的面积是_______ ;
(3)在图中,过点 C 作 O 的切线 CD .
( 图1
图2
第 17 题)
18. (7 分)河上有一座抛物线形的石拱桥,水面宽 6m 时,水面离桥拱顶部 3m,现建
立如图所示坐标系.
(1)求抛物线的解析式;
(2)因暴雨水位上升 1m,一艘装满货物的小船,露出水面部分的高为 0.5m,宽
4m,暴雨后,这艘小船能从这座石拱桥下通过吗?请说明理由.
(第 18 题)
九年级 数学( 共 6 页·第3页)
19.(7 分)如图, AB 是 O的直径, AD平分 BAC ,交 O于点 D,过点 D 作直线
DE ⊥ AC,交 AC 的延长线于点 E,交 AB 的延长线于点 F.
(1)求证: EF 是 O的切线;
(2)过点 O 作OH ⊥ AD,交 AD于点 H,连接BD,若BD = 6, AH = 3 3 ,
则 O的半径= .
(第 19 题)
20.(7 分) 随着近几年我国私家车日愈增多,超速行驶成为引发交通事故的主要原因
之一.某中学数学活动小组为开展“文明驾驶、关爱家人、关爱他人”的活动,设计
了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点P,在笔直的车道m
上确定点 O,使 PO 和 m垂直,测得 PO 的长等于 21 米,在 m 上的同侧取点 A、
B,使∠PAO=30°,∠PBO=60°.
(1)求 A、B 之间的路程(保留根号);
(2)已知本路段对校车限速为 12 米/秒,若测得某校车从 A 到 B 用了 2 秒,这辆
校车是否超速?请说明理由.
(第 20 题)
九年级 数学( 共 6 页·第4页)
1
21.(8 分)利用函数图象探究方程 x x 2 = 的实数根的个数.
2 y
1
(1)设函数 y = x x 2 ,则这个函数的图象与直线 y=
2
1
的交点的_______坐标(填横或纵)就是方程 x x 2 = x
2 O
的实数根.
(2)分类讨论:当 时, y = x2x 2 + 2x ;当 x 2时,
y = ;
(3)在给定的坐标系中,已经画出了当 x 2时的函数图 (第 21 题)
象,请根据(2)中的解析式,通过描点,连线,画出当 x 2时的函数图象.
1 1
(4)在给定的坐标系中画直线 y= ,观察图象可知方程 x x 2 = 的实数根有 个.
2 2
(5)深入探究:若关于x的方程2 x x 2 = m 有3个实数根,则m的取值范围是 .
22. (9 分)【教材原题】如图①,在四边形 ABCD 中,AD=BC,P 是对角线 BD 的中
点,M 是 DC 的中点,N 是 AB 的中点.求证:∠PMN=∠PNM.
【应用】如图②,连结图①中的 AC,并取 AC 中点 Q,连结 MQ、NQ.
(1)若 AD=8 ,则四边形 PMQN 的周长为 .
(2)若 AD=4,且∠DAB+∠ABC=90°,则四边形 PMQN 的面积为 .
M
D C D M C
M CD
P Q P Q
P
A N B A N B A N B
图① 图② 图③
(第 22 题)
九年级 数学( 共 6 页·第5页)
23.(10 分)如图,在□ABCD 中,O 为对角线 BD 的中点,∠ADB=90°,∠A=60°,
AD=4.动点 P 从点 A 出发,以每秒 2 个单位的速度沿折线 AB-BC 向终点 C 匀速运
动.连结 PO 并延长交折线 CD-DA 于点 Q.将线段 PQ 绕着点 P 逆时针旋转 60°得
到线段 PE,连结 QE.设点 P 的运动时间为 t(s).
(1)用含 t 的代数式表示 PB 的长.
(2)当点 P 在边 AB 上运动时,求证:AP=CQ.
(3)当点 E 在△ABD 内部时,求 t 的取值范围.
(4)当△PQE 与△BCD 的重叠部分图形是轴对称的三角形时,直接写出 t 的值.
E
D Q C
O
A P B
(第 23 题)
24.(12 分)在平面直角坐标系中,抛物线 y = x2 + bx + c(b 为常数)顶点 M 的标为
(2,-5),点 P、点 Q 均在这个抛物线上,点 P 的横标为 m,点 Q 的横坐标为
2-m,将此抛物线上 P、Q 两点之间的部分(包括 P、Q 两点)记为图象 G.
(1) b=________, c=________;
(2) 当点 P 与点 Q 重合时,求点 P 的坐标;
(3) 当顶点 M 在图象 G 上时,设图象 G 最高点的纵坐标与最低点的纵标的差为
d,求 d 与 m 之间的函数关系式;
(4) 矩形 ABCD 的顶点分别为 A(1,2)、B(-2-m,2)、C(-2-m,-3),
D(1,-3),当点 P 在点 Q 左侧且图象 G 在形 ABCD 内部的部分所对应
的函数值 y 随 x 的增大而减小或增大而增大时,直接写出 m 的取值范围.
九年级 数学( 共 6 页·第6页)
九年级数学试卷
考试时间:120分钟 总分:120分 出题人:董丽新 一审:张艳秋 终审:肖静纯
一、选择题(共 8小题,每题 3分,共 24分)
1.抛物线 y=x2+1 的顶点是( )
A.(1,0) B.(0,1) C.(0,﹣1) D.(1,1)
2.如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个
点 A、 B 、C 都在横线上.若线段BC = 3cm,则线段 AC 的长是( )
A.3.5cm B.4cm C.4.5cm D.5cm
3. 2 tan45 的值为( )
1
A.1 B. 2 C.2 D.
2
4.某书店拿取高处书籍的登高梯如图位置摆放,登高梯 AC 的顶端 A 恰好放在书架
的第七层的顶端.已知登高梯的长度 AC 为 3 米,登高梯与地面的夹角 ACB 为
72 ,则书架第七层顶端离地面的高度 AB 为( )
3 3
A.3sin72 米 B. 米 C.3cos72 米 D. 米
sin 72 cos 72
(第 2 题) (第 4 题) (第 5 题) (第 6 题)
5. 如图,△ABC 的顶点 A、B、C 均在⊙O 上,若∠ABC=25°,则∠AOC 的大小是
( )
A.25° B.50° C.65° D.75°
6.如图,在△ABC 中,点D、E、F分别为边BC,AD,CE 的中点,S△ABC = 16cm ,
则 S△EBF =( )
A.8cm2 B. 4cm2 C.6cm2 D. 2cm2
九年级 数学( 共 6 页·第1页)
7.某超市经销一种水果,每千克盈利 10 元,每天销售 500 千克,经市场调查反映:
若每千克涨价 1 元,每天销售量减少 20 千克,设每千克涨价 x(单位:元),且
0 x 25,每天售出商品的利润为y(单位:元),则y与x的函数关系式是( )
A. y = 500 20x B. y = (500 20x)(10+ x)
C. y = (500+10x)(10 x) D. y = (500 10x)(10+ x)
k
8.如图,在平面直角坐标系中,点 A、 B 在函数 y = (k 0, x 0) 的图象上,分别
x
以 A、 B 为圆心,1为半径作圆,当 A与 x轴相切、 B与 y 轴相切时,连结
AB, AB = 4 2 ,则 k 的值为( )
A.3 B. 4 2 C.4 D.5
y
A
B O
A x B
O
(第 8 题) (第 11 题) (第 12 题) (第 13 题)
二、填空题(共 6小题,每题 3分,共 18分)
9.已知 O的半径为5cm,若OP = 6cm,那么点 P 在 O .
10.若一元二次方程 x2-2x-3a=0 无实根,则 a 取值范围是 .
11.如图,△ABC 和△DEF 是以点O为位似中心的位似图形,相似比为 2:3,则
△ABC 和△DEF 的面积比是________.
12.如图,小明用自制的直角三角形纸板 DEF 测量树的高度 AB.他调整自己的位
置,设法使斜边 DF 保持水平,并且边 DE 与点 B 在同一直线上,已知纸板的两
条直角边 DE=40cm.EF=30cm,测得边 DF 离地面的高度 AC=1.5m,CD=
10m,求树高 AB 是________m.
13.正方形网格中, AOB如图放置,则sin AOB的值为________.
14.当 x=a 或 x=b(a≠b)时,代数式 x2-4x+2的值相等,则当 x=a+b 时,代数式
x2-4x+2的值为________.
九年级 数学( 共 6 页·第2页)
三、计算题(共 78分)
2 2
15.(6 分)计算:(1) 3 + 3 + 4cos30° 27 (2) x 3x + 2 = 0
16.(6 分)在一个不透明的布袋里装有 4 个球,其中 1 个红球,1 个黄球,2 个白球,
它们除颜色外其余都相同.
(1)若从中任意摸出一个球,摸出白球的概率为 ;
(2)先摸出 1 个球,记下颜色后不放回,再摸出 1 个球,求两次摸出的球恰好一
黄一白的概率(要求画树状图或列表).(设红球为A,黄球为B,白球为C)
17.(6 分)如图,是8 8的正方形网格,每个小正方形的顶点
叫作格点.A、B、C、D 四点是格点且在圆上, 仅用无
A B A B
刻度的直尺在给定网格中完成画图 .
(1)在图中,画出经过 A、B、C 这三点的圆的圆心 O ;
C D C
(2)在图中, O 的面积是_______ ;
(3)在图中,过点 C 作 O 的切线 CD .
( 图1
图2
第 17 题)
18. (7 分)河上有一座抛物线形的石拱桥,水面宽 6m 时,水面离桥拱顶部 3m,现建
立如图所示坐标系.
(1)求抛物线的解析式;
(2)因暴雨水位上升 1m,一艘装满货物的小船,露出水面部分的高为 0.5m,宽
4m,暴雨后,这艘小船能从这座石拱桥下通过吗?请说明理由.
(第 18 题)
九年级 数学( 共 6 页·第3页)
19.(7 分)如图, AB 是 O的直径, AD平分 BAC ,交 O于点 D,过点 D 作直线
DE ⊥ AC,交 AC 的延长线于点 E,交 AB 的延长线于点 F.
(1)求证: EF 是 O的切线;
(2)过点 O 作OH ⊥ AD,交 AD于点 H,连接BD,若BD = 6, AH = 3 3 ,
则 O的半径= .
(第 19 题)
20.(7 分) 随着近几年我国私家车日愈增多,超速行驶成为引发交通事故的主要原因
之一.某中学数学活动小组为开展“文明驾驶、关爱家人、关爱他人”的活动,设计
了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点P,在笔直的车道m
上确定点 O,使 PO 和 m垂直,测得 PO 的长等于 21 米,在 m 上的同侧取点 A、
B,使∠PAO=30°,∠PBO=60°.
(1)求 A、B 之间的路程(保留根号);
(2)已知本路段对校车限速为 12 米/秒,若测得某校车从 A 到 B 用了 2 秒,这辆
校车是否超速?请说明理由.
(第 20 题)
九年级 数学( 共 6 页·第4页)
1
21.(8 分)利用函数图象探究方程 x x 2 = 的实数根的个数.
2 y
1
(1)设函数 y = x x 2 ,则这个函数的图象与直线 y=
2
1
的交点的_______坐标(填横或纵)就是方程 x x 2 = x
2 O
的实数根.
(2)分类讨论:当 时, y = x2x 2 + 2x ;当 x 2时,
y = ;
(3)在给定的坐标系中,已经画出了当 x 2时的函数图 (第 21 题)
象,请根据(2)中的解析式,通过描点,连线,画出当 x 2时的函数图象.
1 1
(4)在给定的坐标系中画直线 y= ,观察图象可知方程 x x 2 = 的实数根有 个.
2 2
(5)深入探究:若关于x的方程2 x x 2 = m 有3个实数根,则m的取值范围是 .
22. (9 分)【教材原题】如图①,在四边形 ABCD 中,AD=BC,P 是对角线 BD 的中
点,M 是 DC 的中点,N 是 AB 的中点.求证:∠PMN=∠PNM.
【应用】如图②,连结图①中的 AC,并取 AC 中点 Q,连结 MQ、NQ.
(1)若 AD=8 ,则四边形 PMQN 的周长为 .
(2)若 AD=4,且∠DAB+∠ABC=90°,则四边形 PMQN 的面积为 .
M
D C D M C
M CD
P Q P Q
P
A N B A N B A N B
图① 图② 图③
(第 22 题)
九年级 数学( 共 6 页·第5页)
23.(10 分)如图,在□ABCD 中,O 为对角线 BD 的中点,∠ADB=90°,∠A=60°,
AD=4.动点 P 从点 A 出发,以每秒 2 个单位的速度沿折线 AB-BC 向终点 C 匀速运
动.连结 PO 并延长交折线 CD-DA 于点 Q.将线段 PQ 绕着点 P 逆时针旋转 60°得
到线段 PE,连结 QE.设点 P 的运动时间为 t(s).
(1)用含 t 的代数式表示 PB 的长.
(2)当点 P 在边 AB 上运动时,求证:AP=CQ.
(3)当点 E 在△ABD 内部时,求 t 的取值范围.
(4)当△PQE 与△BCD 的重叠部分图形是轴对称的三角形时,直接写出 t 的值.
E
D Q C
O
A P B
(第 23 题)
24.(12 分)在平面直角坐标系中,抛物线 y = x2 + bx + c(b 为常数)顶点 M 的标为
(2,-5),点 P、点 Q 均在这个抛物线上,点 P 的横标为 m,点 Q 的横坐标为
2-m,将此抛物线上 P、Q 两点之间的部分(包括 P、Q 两点)记为图象 G.
(1) b=________, c=________;
(2) 当点 P 与点 Q 重合时,求点 P 的坐标;
(3) 当顶点 M 在图象 G 上时,设图象 G 最高点的纵坐标与最低点的纵标的差为
d,求 d 与 m 之间的函数关系式;
(4) 矩形 ABCD 的顶点分别为 A(1,2)、B(-2-m,2)、C(-2-m,-3),
D(1,-3),当点 P 在点 Q 左侧且图象 G 在形 ABCD 内部的部分所对应
的函数值 y 随 x 的增大而减小或增大而增大时,直接写出 m 的取值范围.
九年级 数学( 共 6 页·第6页)
同课章节目录
