第三章 圆锥曲线的方程(章末总结)-高中数学人教A版(2019)选择性必修第一册 课件(共34张PPT)
文档属性
| 名称 | 第三章 圆锥曲线的方程(章末总结)-高中数学人教A版(2019)选择性必修第一册 课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 31.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-24 20:19:35 | ||
图片预览










文档简介
(共34张PPT)
章末总结
第 三 章 圆锥曲线的方程
人教A版2019选修第一册
01知识结构
PART ONE
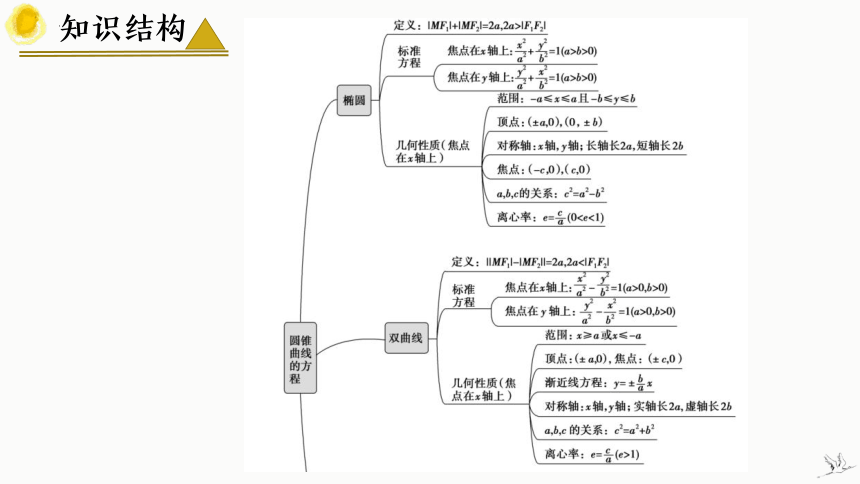
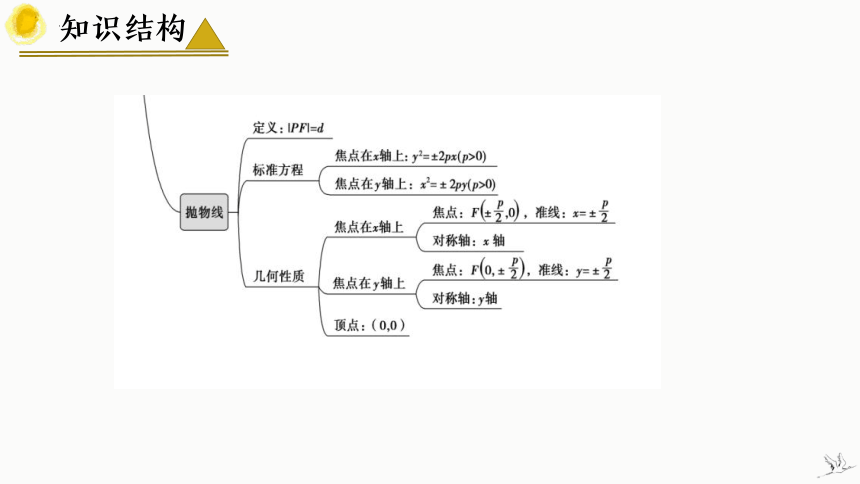
知识结构
知识结构
02圆锥曲线的方程的应用
PART ONE
知识应用
1.圆锥曲线的定义及应用
例1.(1)一动圆与两圆:x2+y2=1和x2+y2-6x+5=0都外切,则动圆圆心的轨迹为( )
A.抛物线 B.双曲线
C.双曲线的一支 D.椭圆
(2)在平面直角坐标系xOy中,椭圆C的中心为原点,焦点F1,F2在x轴上,离心率为 .过F1的直线l交C于A,B两点,且△ABF2的周长为16,那么C的方程为________.
+=1
C
(3)已知动点M的坐标满足方程 =|3x+4y-12|,则动点M的轨迹是( )
A.椭圆 B.双曲线 C.抛物线 D.以上都不对
C
知识应用
解: (1)x2+y2=1是圆心为原点,半径为1的圆,
x2+y2-6x+5=0化为标准方程为(x-3)2+y2=4,是圆心为A(3,0),半径为2的圆.
设所求动圆圆心为P,动圆半径为r,则 |PA|-|PO|=1<|AO|=3,
符合双曲线的定义,所以动圆圆心的轨迹为双曲线的一支.
(2)设椭圆方程为 +=1(a>b>0),因为AB过F1且A,B在椭圆上,如图所示,
则△ABF2的周长为|AB|+|AF2|+|BF2|=|AF1|+|AF2|+|BF1|+|BF2|=4a=16,∴a=4.
又离心率e==,∴c=2,∴b2=a2-c2=8,
∴椭圆C的方程为 +=1.
知识应用
∴动点M到原点的距离与它到直线3x+4y-12=0的距离相等.
∴点M的轨迹是以原点为焦点,直线3x+4y-12=0为准线的抛物线.
知识应用
例2.一动圆与圆x2+y2+6x+5=0外切,同时与圆x2+y2-6x-91=0内切,求动圆圆心M的轨迹方程,并说明它是什么样的曲线.
解:设动圆圆心为M(x,y),半径为R,设已知圆的圆心分别为O1,O2.
将圆的方程分别配方,得(x+3)2+y2=4,(x-3)2+y2=100,以O1O2所在直线为x轴,其中垂线为y轴建立如图所示的直角坐标系.
当圆M与圆O1外切时,有|O1M|=R+2; ①
当圆M与圆O2内切时,有|O2M|=10-R. ②
将①②两式的两边分别相加,
得|O1M|+|O2M|=12>|O1O2|=6.
根据椭圆的定义,圆心M的轨迹是以O1,O2为焦点的椭圆,且a=6,c=3,b2=a2-c2=27.
故动圆圆心M的轨迹方程是+=1,且轨迹是焦点在x轴上,长、短半轴长分别为6、3的椭圆.
知识应用
【类题通法】 “回归定义”解题的三点应用
应用一:在求轨迹方程时,若所求轨迹符合某种圆锥曲线的定义,则根据圆锥曲线的定义,写出所求的轨迹方程;
应用二:涉及椭圆、双曲线上的点与两个定点构成的三角形问题时,常用定义结合解三角形的知识来解决;
应用三:在求有关抛物线的最值问题时,常利用定义把到焦点的距离转化为到准线的距离,结合几何图形,利用几何意义去解决.
提醒:应用定义解题时注意圆锥曲线定义中的限制条件.
知识应用
知识应用
知识应用
知识应用
知识应用
2.圆锥曲线的性质及应用
例3(1)若椭圆 +=1(a>b>0)的离心率为,则双曲线 -=1的渐近线方程为( )
A.y=±x B.y=±2x C.y=±4x D.y=±x
(2)已知双曲线 (a>0,b>0)的左焦点为F,离心率为.若经过F和P(0,4)两点的直线平行于双曲线的一条渐近线,则双曲线的方程为( )
A. =1 B.=1 C.=1 D.=1
A
B
知识应用
解:(1)由椭圆的离心率e==,可知 =,∴ =,故双曲线的渐近线方程为y=±x.
(2)由题意可得 =,即c=a.又左焦点F(-c,0),P(0,4).
则直线PF的方程为=,化简即得y=x+4.
结合已知条件和图象易知直线PF与y=x平行,
则=,即4a=bc.
故解得 故双曲线方程为=1.
知识应用
A
知识应用
知识应用
【类题通法】
1.圆锥曲线的几何性质主要包括范围、对称性、焦点、顶点、长短轴(椭圆)、实虚轴(双曲线)、渐近线(双曲线)、离心率和准线(抛物线).
2.椭圆的离心率,双曲线的离心率和渐近线,抛物线的焦点和准线,都是常考的性质,要熟练掌握.
知识应用
3.圆锥曲线中的定值、定点问题
知识应用
知识应用
知识应用
知识应用
【类题通法】 圆锥曲线中的定值、定点问题
(1)定值问题的常见类型及解题策略
①求代数式为定值.依题意设条件,得出与代数式参数有关的等式,代入代数式、化简即可得出定值.
②求点到直线的距离为定值.利用点到直线的距离公式得出距离的解析式,再利用题设条件化简、变形求得.
③求某线段长度为定值.利用长度公式求得解析式,再依据条件对解析式进行化简、变形即可求得.
(2)定点问题的两种解法
①引进参数法:引进动点的坐标或动线中系数为参数表示变化量,再研究变化的量与参数何时没有关系,找到定点.
②特殊到一般法:根据动点或动线的特殊情况探索出定点,再证明该定点与变量无关.
知识应用
练习:过点C(0,1)的椭圆 +=1(a>b>0)的离心率为,椭圆与x轴交于两点A(a,0),B(-a,0),过点C的直线l与椭圆交于另一点D,并与x轴交于点P,直线AC与直线BD交于点Q.、
(1)当直线l过椭圆右焦点时,求线段CD的长;
(2)当点P异于点B时,求证:· 为定值.
(1) 解:由已知得b=1,=,解得a=2,c=,所以椭圆方程为+y2=1.
椭圆的右焦点为(,0),此时直线l的方程为y=-x+1,
代入椭圆方程化简得7x2-8x=0,解得x1=0,x2=,
代入直线l的方程得y1=1,y2=-,所以D点的坐标为.
故|CD|= =.
知识应用
(2)证明:当直线l与x轴垂直时与题意不符.
设直线l的方程为y=kx+1(k≠0且k≠),
代入椭圆方程化简得(4k2+1)x2+8kx=0,解得x1=0,x2=,
代入直线l的方程得y1=1,y2=,所以D点坐标为.
又直线AC的方程为+y=1,直线BD的方程为y=(x+2),
联立解得,因此Q点坐标为(-4k,2k+1).
又P点坐标为,所以 ·=·(-4k,2k+1)=4.
故 · 为定值.
知识应用
4.圆锥曲线中的证明与探索性问题
知识应用
知识应用
知识应用
知识应用
知识应用
知识应用
知识应用
章末总结
第 三 章 圆锥曲线的方程
人教A版2019选修第一册
01知识结构
PART ONE
知识结构
知识结构
02圆锥曲线的方程的应用
PART ONE
知识应用
1.圆锥曲线的定义及应用
例1.(1)一动圆与两圆:x2+y2=1和x2+y2-6x+5=0都外切,则动圆圆心的轨迹为( )
A.抛物线 B.双曲线
C.双曲线的一支 D.椭圆
(2)在平面直角坐标系xOy中,椭圆C的中心为原点,焦点F1,F2在x轴上,离心率为 .过F1的直线l交C于A,B两点,且△ABF2的周长为16,那么C的方程为________.
+=1
C
(3)已知动点M的坐标满足方程 =|3x+4y-12|,则动点M的轨迹是( )
A.椭圆 B.双曲线 C.抛物线 D.以上都不对
C
知识应用
解: (1)x2+y2=1是圆心为原点,半径为1的圆,
x2+y2-6x+5=0化为标准方程为(x-3)2+y2=4,是圆心为A(3,0),半径为2的圆.
设所求动圆圆心为P,动圆半径为r,则 |PA|-|PO|=1<|AO|=3,
符合双曲线的定义,所以动圆圆心的轨迹为双曲线的一支.
(2)设椭圆方程为 +=1(a>b>0),因为AB过F1且A,B在椭圆上,如图所示,
则△ABF2的周长为|AB|+|AF2|+|BF2|=|AF1|+|AF2|+|BF1|+|BF2|=4a=16,∴a=4.
又离心率e==,∴c=2,∴b2=a2-c2=8,
∴椭圆C的方程为 +=1.
知识应用
∴动点M到原点的距离与它到直线3x+4y-12=0的距离相等.
∴点M的轨迹是以原点为焦点,直线3x+4y-12=0为准线的抛物线.
知识应用
例2.一动圆与圆x2+y2+6x+5=0外切,同时与圆x2+y2-6x-91=0内切,求动圆圆心M的轨迹方程,并说明它是什么样的曲线.
解:设动圆圆心为M(x,y),半径为R,设已知圆的圆心分别为O1,O2.
将圆的方程分别配方,得(x+3)2+y2=4,(x-3)2+y2=100,以O1O2所在直线为x轴,其中垂线为y轴建立如图所示的直角坐标系.
当圆M与圆O1外切时,有|O1M|=R+2; ①
当圆M与圆O2内切时,有|O2M|=10-R. ②
将①②两式的两边分别相加,
得|O1M|+|O2M|=12>|O1O2|=6.
根据椭圆的定义,圆心M的轨迹是以O1,O2为焦点的椭圆,且a=6,c=3,b2=a2-c2=27.
故动圆圆心M的轨迹方程是+=1,且轨迹是焦点在x轴上,长、短半轴长分别为6、3的椭圆.
知识应用
【类题通法】 “回归定义”解题的三点应用
应用一:在求轨迹方程时,若所求轨迹符合某种圆锥曲线的定义,则根据圆锥曲线的定义,写出所求的轨迹方程;
应用二:涉及椭圆、双曲线上的点与两个定点构成的三角形问题时,常用定义结合解三角形的知识来解决;
应用三:在求有关抛物线的最值问题时,常利用定义把到焦点的距离转化为到准线的距离,结合几何图形,利用几何意义去解决.
提醒:应用定义解题时注意圆锥曲线定义中的限制条件.
知识应用
知识应用
知识应用
知识应用
知识应用
2.圆锥曲线的性质及应用
例3(1)若椭圆 +=1(a>b>0)的离心率为,则双曲线 -=1的渐近线方程为( )
A.y=±x B.y=±2x C.y=±4x D.y=±x
(2)已知双曲线 (a>0,b>0)的左焦点为F,离心率为.若经过F和P(0,4)两点的直线平行于双曲线的一条渐近线,则双曲线的方程为( )
A. =1 B.=1 C.=1 D.=1
A
B
知识应用
解:(1)由椭圆的离心率e==,可知 =,∴ =,故双曲线的渐近线方程为y=±x.
(2)由题意可得 =,即c=a.又左焦点F(-c,0),P(0,4).
则直线PF的方程为=,化简即得y=x+4.
结合已知条件和图象易知直线PF与y=x平行,
则=,即4a=bc.
故解得 故双曲线方程为=1.
知识应用
A
知识应用
知识应用
【类题通法】
1.圆锥曲线的几何性质主要包括范围、对称性、焦点、顶点、长短轴(椭圆)、实虚轴(双曲线)、渐近线(双曲线)、离心率和准线(抛物线).
2.椭圆的离心率,双曲线的离心率和渐近线,抛物线的焦点和准线,都是常考的性质,要熟练掌握.
知识应用
3.圆锥曲线中的定值、定点问题
知识应用
知识应用
知识应用
知识应用
【类题通法】 圆锥曲线中的定值、定点问题
(1)定值问题的常见类型及解题策略
①求代数式为定值.依题意设条件,得出与代数式参数有关的等式,代入代数式、化简即可得出定值.
②求点到直线的距离为定值.利用点到直线的距离公式得出距离的解析式,再利用题设条件化简、变形求得.
③求某线段长度为定值.利用长度公式求得解析式,再依据条件对解析式进行化简、变形即可求得.
(2)定点问题的两种解法
①引进参数法:引进动点的坐标或动线中系数为参数表示变化量,再研究变化的量与参数何时没有关系,找到定点.
②特殊到一般法:根据动点或动线的特殊情况探索出定点,再证明该定点与变量无关.
知识应用
练习:过点C(0,1)的椭圆 +=1(a>b>0)的离心率为,椭圆与x轴交于两点A(a,0),B(-a,0),过点C的直线l与椭圆交于另一点D,并与x轴交于点P,直线AC与直线BD交于点Q.、
(1)当直线l过椭圆右焦点时,求线段CD的长;
(2)当点P异于点B时,求证:· 为定值.
(1) 解:由已知得b=1,=,解得a=2,c=,所以椭圆方程为+y2=1.
椭圆的右焦点为(,0),此时直线l的方程为y=-x+1,
代入椭圆方程化简得7x2-8x=0,解得x1=0,x2=,
代入直线l的方程得y1=1,y2=-,所以D点的坐标为.
故|CD|= =.
知识应用
(2)证明:当直线l与x轴垂直时与题意不符.
设直线l的方程为y=kx+1(k≠0且k≠),
代入椭圆方程化简得(4k2+1)x2+8kx=0,解得x1=0,x2=,
代入直线l的方程得y1=1,y2=,所以D点坐标为.
又直线AC的方程为+y=1,直线BD的方程为y=(x+2),
联立解得,因此Q点坐标为(-4k,2k+1).
又P点坐标为,所以 ·=·(-4k,2k+1)=4.
故 · 为定值.
知识应用
4.圆锥曲线中的证明与探索性问题
知识应用
知识应用
知识应用
知识应用
知识应用
知识应用
知识应用
