人教版六年级上册数学第四单元比(知识点梳理+能力百分练)五(学案)
文档属性
| 名称 | 人教版六年级上册数学第四单元比(知识点梳理+能力百分练)五(学案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1007.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-24 21:41:17 | ||
图片预览





文档简介
中小学教育资源及组卷应用平台
人教版六年级上册第四单元比(知识点梳理+能力百分练)五
知识点梳理
1、比的意义:两个数的比表示两个数相除。
2、比的各部分的名称:从左到右依次是比的前项、比号、比的后项。
3、区分比和比值:比是一个式子,表示两个数的关系,可以写成比的形式,也可以写成分数的形式。比值是一个数,通常用分数表示,也可以用整数或小数表示。
4、比的基本性质:比的前项和后项同时乘或除以相同的数(0除外),比值不变。
5、化简比:根据比的基本性质,可以把比化简成最简单的整数比。
6、按比例分配:把一个量按一定的比例分配的方法叫做按比例分配。
能力百分练
一、选择题(共16分)
1.若a、b是两个非0的自然数,a>b,则(a+b)∶a的比值( )。
A.是0到1之间的数 B.是1到2之间的数
C.有可能是2 D.有可能大于2
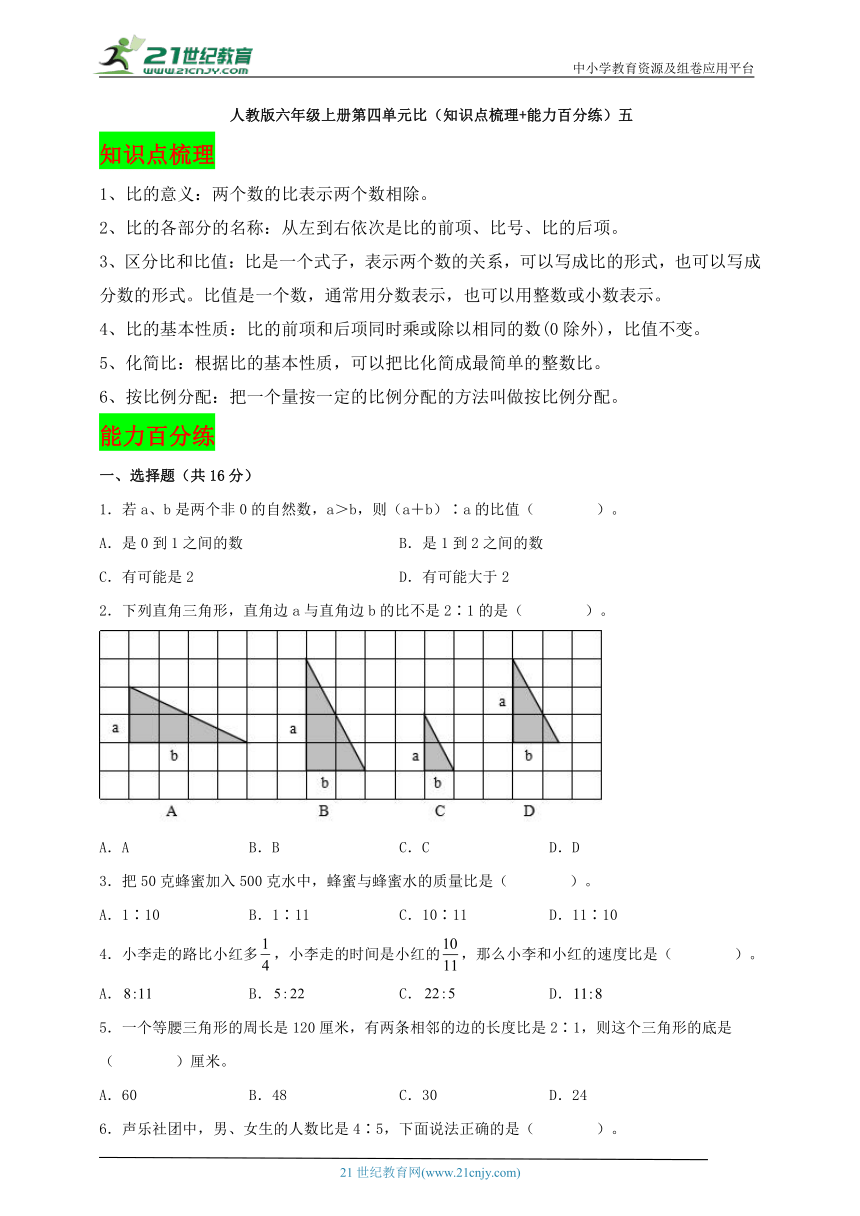
2.下列直角三角形,直角边a与直角边b的比不是2∶1的是( )。
A.A B.B C.C D.D
3.把50克蜂蜜加入500克水中,蜂蜜与蜂蜜水的质量比是( )。
A.1∶10 B.1∶11 C.10∶11 D.11∶10
4.小李走的路比小红多,小李走的时间是小红的,那么小李和小红的速度比是( )。
A. B. C. D.
5.一个等腰三角形的周长是120厘米,有两条相邻的边的长度比是2∶1,则这个三角形的底是( )厘米。
A.60 B.48 C.30 D.24
6.声乐社团中,男、女生的人数比是4∶5,下面说法正确的是( )。
A.女生人数是男生人数的 B.男生人数比女生人数少
C.女生人数比男生人数多 D.女生人数占社团总人数的
7.在4∶5中,如果比的后项增加10,要使比值不变,比的前项应( )。
A.乘2 B.乘3 C.增加10 D.减少10
8.小丽和小红从学校去图书馆,小丽需要9分钟,小红需要6分钟。小丽和小红的速度比是( )。
A.9∶6 B.3∶2 C.2∶3 D.∶
二、填空题(共16分)
9.把3.75∶1.8化成最简整数比是( ),比值是( )。
10.工程队挖一条水渠,已经挖了1200m,已经挖的米数与未挖米数的比是3∶5,这条水渠全长( )m。
11.有两堆小麦,甲堆小麦质量的正好等于乙堆质量的。甲乙两堆小麦质量的比是( )∶( )。
12.教室地面的周长是36m,长与宽的比是5∶4。这个教室的地面面积是( )m2。
13.如图,小新家的院子被分成5个形状、大小都相同的长方形,每个长方形的周长是10米,那么院子的周长是( )米。
14.一件衬衣的售价为100元,一条裤子的售价和衬衣的售价之比是;这条裤子的售价为( )元。
15.图书馆上午借出20本书籍,下午借出36本书籍,图书馆上午和下午借出的书籍的本数比是( )(填最简单的整数比),比值是( )。
16.一个等腰三角形,它的顶角与一个底角的度数比是1∶2,这个三角形中最大的内角度数是( )。
三、判断题(共8分)
17.甲数和乙数的比是2∶3,乙数和丙数的比是4∶5,则甲数∶丙数=2∶5。( )
18.上衣比裤子贵,则上衣和裤子的价格比是7∶2。( )
19.一个长方形的周长是36厘米,长和宽的比是2∶1,它的面积是288平方厘米。( )
20.红红和老师今年的年龄比为1∶9,10年后,他们的年龄比不变。( )
四、计算题(共6分)
21.(6分)化简比。
升∶350毫升
五、作图题(共6分)
22.(6分)画一个面积为12平方厘米的直角三角形,要求两条直角边比为3∶2。(每一格边长1厘米)
六、解答题(共48分)
23.(6分)相同质量的冰和水的体积之比是10∶9。现有体积为45升的水,结成冰后的体积是多少立方分米?
24.(6分)学校武术队的男队员比女队员多24名,已知男、女队员人数的比是7∶5,则女队员与男队员各有多少名?
25.(6分)书法组和朗诵组的人数比为7∶5,如果将书法组的10名同学调到朗诵组去,这时书法组和朗诵组的人数比为4∶5,原来书法组有多少人?
26.(6分)水果店运来苹果比橙子少240千克,已知苹果与橙子的质量比是3∶5,水果店运来苹果和橙子一共多少千克?
27.(6分)果园里苹果树比桃树多90棵,苹果树的棵数与桃树的棵数比为5∶2,果园里苹果树、桃树各多少棵?
28.(6分)一只鱼塘按4∶5放养鲢鱼和鲤鱼,一共可以放养4500尾,其中鲢鱼的鱼苗应放养多少尾?
29.(6分)2022年12月22日是“冬至”,是一年中白昼最短、黑夜最长的一天。这天绍兴的白昼与黑夜时间比约是5∶7,而“中国最北端”的漠河县的白昼与黑夜时间比约是1∶2。
(1)“冬至”这一天绍兴的白昼约有几小时?
(2)“冬至”这一天,绍兴的黑夜时间是漠河黑夜时间的几分之几?
30.(6分)工程队正在进行道路抢修,要求三小时修好一条560米的公路,第一个小时修了全长的,第二小时和第三小时修的长度比是3∶4,问:这三小时,哪一小时修的路最长?
参考答案
1.B
【分析】两个不为0的数相除,如果被除数大于除数,则商大于1;根据分数和比的关系,可知(a+b)∶a=,根据分数加法的意义,可得=1+;如果分子小于分母,则分数值小于1,据此解答即可。
【详解】a+b>a
根据比和除法的关系,可知(a+b)∶a的比值一定大于1;
(a+b)∶a
=
=+
=1+
a>b
所以<1
1+<2
据此可知,(a+b)∶a的比值是1到2之间的数。
故答案为:B
【点睛】本题可根据比和分数、除法之间的关系进行解答。
2.A
【分析】两数相除又叫两个数的比,分别数出各三角形直角边格数,写出a与b的比,能化简的化简即可。
【详解】A.2∶4=1∶2
B.4∶2=2∶1
C.2∶1
D.3∶1.5=30∶15=2∶1
故答案为:A
【点睛】关键是理解比的意义,掌握化简比的方法。
3.B
【分析】根据题意,先用蜂蜜的质量加上水的质量,求出蜂蜜水的质量;然后根据比的意义写出蜂蜜与蜂蜜水的质量比,再化简比即可。
【详解】50∶(50+500)
=50∶550
=(50÷50)∶(550÷50)
=1∶11
蜂蜜与蜂蜜水的质量比是1∶11。
故答案为:B
【点睛】本题考查比的意义及化简比。注意化简比的结果是一个比,它的前项和后项都是整数,并且是互质数。
4.A
【分析】小李走的路比小红多,将小红走的路看作4,则小李走的路是(4+1),小李走的时间是小红的,将小红走的时间看作11,则小李走的时间是10,速度=路程÷时间,据此表示出两人走的速度,写出速度比,化简即可。
【详解】小李速度:10÷(4+1)
=10÷5
=2
小红速度:11÷4=
小李和小红的速度比:2∶=(2×4)∶(×4)=8∶11
故答案为:A
【点睛】关键是理解速度、时间、路程之间的关系,理解分数和比的意义。
5.D
【分析】根据三角形三边关系,可以确定这个等腰三角形的3条边的比是2∶2∶1,共(2+2+1)份,求出一份数就是等腰三角形的底。
【详解】120×
=120×
=24(厘米)
则三角形的底是24厘米。
故答案为:D
【点睛】关键是熟悉三角形三边关系和等腰三角形的特征,理解比的意义。
6.B
【分析】把男生的人数看作“4”,则女生人数是“5”,总人数是“(4+5)”。
A.求女生人数是男生人数的几分之几,用女生人数除以男生人数。
B.求男生人数比女生人数少几分之几,用男、女生人数之差除以女生人数。
C.求女生人数比男生人数多几分之几,用男、女生人数之差除以男生人数。
D.求女生人数是社团人数的几分之几,用女生人数除以总人数,据此解答。
【详解】由分析可得:
A.5÷4=,女生人数是男生人数的,选项说法错误;
B.(5-4)÷5
=1÷5
=
男生人数比女生人数少,选项说法正确;
C.(5-4)÷4
=1÷4
=
女生人数比男生人数多,选项说法错误;
D.5÷(4+5)
=5÷9
=
女生人数占社团总人数的,选项说法错误。
故答案为:B
【点睛】求一个数是另一个数的几分之几,用这个数除以另一个数;求一个数比另一个数多或少几分之几,用这两数之差除以另一个数。
7.B
【分析】依据比的性质,即比的前项和后同时乘或除以一个不等于零的数,比的大小不变,即可求解。
【详解】4∶5,比的后项5增加10就变成15,就相当于扩大到原来的15÷5=3倍,
若使比值不变,前项也应扩大到原来的3倍,则变成4×3=12。
故答案为:B
【点睛】解答此题的关键是:看比的前项扩大到原来的几倍,比的后项也扩大相同的倍数,就能保证比值不变。
8.C
【分析】把从学校到图书馆的路程看作单位“1”,根据“路程÷时间=速度”分别求出小丽和小红的速度,进而根据题意求比即可判断。
【详解】(1÷9)∶(1÷6)
=∶
=(×54÷3)∶(×54÷3)
=2∶3
小丽和小红的速度比是2∶3。
故答案为:C
【点睛】解答此题用到的知识点:(1)比的意义;(2)路程、时间和速度三者之间的关系。
9. 25∶12
【分析】第一空根据比的基本性质作答,即比的前项和后项同时乘一个数或除以一个数(0除外)比值不变。第二空用最简整数比中比的前项除以后项即可。
【详解】3.75∶1.8
=(3.75÷0.15)∶(1.8÷0.15)
=25∶12
25∶12
=25÷12
=
即把3.75∶1.8化成最简整数比是25∶12,比值是。
【点睛】此题主要考查了化简比和求比值的方法,另外还要注意化简比的结果是一个比,它的前项和后项都是整数,并且是互质数;而求比值的结果是一个商,可以是整数,小数或分数。
10.3200
【分析】已经挖的米数与未挖米数的比是3∶5,说明已挖的长度是整条水渠长的,用已经挖的长度除以它占全长的分率,求出全长即可。
【详解】(m)
所以这条水渠全长3200m。
【点睛】本题考查按比分配,解答本题的关键是掌握按比分配解题的计算方法。
11. 2 3
【分析】根据“甲堆小麦质量的正好等于乙堆质量的”可得出,甲堆小麦质量×=乙堆质量×,两个乘法算式的积相等,可以设它们积都等于1;
然后根据“因数=积÷另一个因数”,分别求出甲堆小麦质量、乙堆小麦质量的值;
再根据比的意义,写出甲乙两堆小麦质量的比,并根据比的基本性质化简比。
【详解】设甲堆小麦质量×=乙堆质量×=1;
甲堆小麦质量=1÷=1×=
乙堆质量=1÷=1×4=4
甲堆小麦质量∶乙堆质量
=∶4
=(×3)∶(4×3)
=8∶12
=(8÷4)∶(12÷4)
=2∶3
甲乙两堆小麦质量的比是2∶3。
【点睛】运用赋值法,根据乘法中各部分的关系计算出甲堆小麦质量、乙堆小麦质量的值,再根据比的意义和比的化简解答。
12.80
【分析】根据长方形的周长公式:C=2(a+b),用36除以2即可求出该长方形的长与宽的和,再根据按比分配问题,求出长方形的长和宽的值,最后根据长方形的面积公式:S=ab,据此计算即可。
【详解】36÷2=18(m)
18÷(5+4)
=18÷9
=2(m)
2×5=10(m)
2×4=8(m)
10×8=80(m2)
则这个教室的地面面积是80m2。
【点睛】本题考查按比分配问题,结合长方形的周长和面积的计算方法是解题的关键。
13.22
【分析】已知每个小长方形的周长是10米,根据长方形的长、宽之和=周长÷2,求出小长方形长、宽的和;
从图中可知,2个小长方形的长等于3个小长方形的宽,则小长方形的长、宽之比是3∶2,即长、宽各占长、宽之和的、,根据求一个数的几分之几是多少,用乘法分别求出小长方形的长和宽;
从图中可知,院子的长等于小长方形长的2倍,院子的宽等于小长方形的长加宽,由此求出院子的长和宽,然后根据长方形的周长=(长+宽)×2,代入数据计算,即可求出这个院子的周长。
【详解】小长方形的长、宽之比是3∶2;
小长方形的长、宽之和:10÷2=5(米)
长:5×=3(米)
宽:5×=2(米)
院子的长:3×2=6(米)
院子的宽:3+2=5(米)
院子的周长:
(6+5)×2
=11×2
=22(米)
院子的周长是22米。
【点睛】本题考查按比分配问题以及长方形周长公式的灵活运用,从图中找出小长方形的长、宽之比,然后把比转化成分数,根据分数乘法的意义求出每个小长方形的长、宽是解题的关键。
14.150
【分析】已知两个数量的比和其中的一个数量,求另外一个数量的解题方法:已知量÷对应的份数=每份的量,每份量×相应份数=对应的量。此题中100元对应2份,用100÷2先求出每份的钱数,再用每份的钱数乘3求出这条裤子的售价。
【详解】100÷2×3
=50×3
=150(元)
所以这条裤子的售价为150元。
【点睛】解按比分配的问题时,一定要注意已知量所对应的份数是多少。
15. 5∶9
【分析】根据比的意义,写出图书馆上午和下午借出的书籍的本数比,再根据比的基本性质,比的前项和后项同时乘一个数或除以一个数(0除外)化简比;最后用比的前项除以后项即可。
【详解】20∶36
=(20÷4)∶(36÷4)
=5∶9
图书馆上午和下午借出的书籍的本数比是5∶9;
5∶9
=5÷9
=
比值是。
【点睛】此题主要考查了化简比和求比值的方法,另外还要注意化简比的结果是一个比,它的前项和后项都是整数,并且是互质数;而求比值的结果是一个商,可以是整数,小数或分数。
16.72度/72°
【分析】根据等腰三角形的特征,可知两个底角相等,可知三个角度的比是1∶2∶2,把三角形的三个内角分别看作1份、2份和2份,已知三角形的内角和是180度,用180÷(1+2+2)即可求出每份是多少,进而求出2份是多少,也就是最大的内角度数。
【详解】180÷(1+2+2)
=180÷5
=36(度)
36×2=72(度)
这个三角形中最大的内角度数是72度。
【点睛】本题考查了比的应用,明确三角形内角和是180度以及等腰三角形的特征是解题的关键。
17.×
【分析】根据比的基本性质,比的前项和后项同时乘或除以一个不为0的数,比值不变,据此化为三联比即可求解。
【详解】甲数∶乙数=2∶3=8∶12
乙数∶丙数=4∶5=12∶15
可得甲数∶乙数∶丙数=8∶12∶15
所以甲数∶丙数=8∶15。
故答案为:×
【点睛】本题考查比的性质,熟练运用比的基本性质是解题的关键。
18.×
【分析】假设裤子为100元,根据题意可知,上衣比裤子贵,把裤子的价格看作单位“1”,上衣的价格是裤子的(1+),根据分数乘法的意义,用100×(1+)即可求出上衣的价格,最后写出上衣和裤子的价格比,再化简即可,化简比根据比的基本性质作答,即比的前项和后项同时乘或除以一个数(0除外),比值不变。据此解答。
【详解】假设裤子为100元,
上衣:100×(1+)
=100×
=140(元)
140∶100
=(140÷20)∶(100÷20)
=7∶5
上衣比裤子贵,则上衣和裤子的价格比是7∶5。原题干说法错误。
故答案为:×
【点睛】本题考查了分数和比的关系的转化,可用假设法解决问题。
19.×
【分析】根据长方形的周长=(长+宽)×2,已知长方形的周长是36厘米,则用36÷2即可求出长与宽的和,又已知长和宽的比是2∶1,把长看作2份,宽看作1份,用36÷2÷(2+1)即可求出每份是多少,进而求出长和宽,最后根据长方形的面积公式求解即可。
【详解】36÷2÷(2+1)
=18÷3
=6(厘米)
6×2=12(厘米)
6×1=6(厘米)
12×6=72(平方厘米)
即它的面积是72平方厘米。
故答案为:×
【点睛】本题主要考查了按比分配问题,熟记长方形周长公式和面积公式是解题的关键。
20.×
【分析】比的前项和后项,同时乘或除以相同的数(0除外),比值不变,据此分析。
【详解】红红和老师今年的年龄比为1∶9,10年后,相当于年龄比的前项和后项同时加上10,年龄比会改变,所以原题说法错误。
故答案为:×
【点睛】关键是掌握并灵活运用比的基本性质。
21.8∶9;4∶1;5∶7
【分析】(1)根据比的基本性质比的前项和后项同时乘3和4的最小公倍数12。
(2)根据比的基本性质比的前项和后项同时乘100,把小数比转化为整数比128∶32;再把整数比的前项和后项同时除以128和32的最大公因数32。
(3)先把升换算为250毫升;再把比的前项和后项同时除以250和350的最大公因数50。
【详解】
=
=8∶9
=
=128∶32
=(128÷32)∶(32÷32)
=4∶1
升∶350毫升
=250毫升∶350毫升
=250∶350
=(250÷50)∶(350÷50)
=5∶7
22.见详解
【分析】因为三角形是一个直角三角形,则三角形的两条直角边相当于三角形的底和高,又已知三角形的面积为12平方厘米,两条直角边比为3∶2,设直角边为3x厘米,另一条直角边为2x厘米,根据三角形的面积公式可得,3x×2x÷2=12,据此求出x=4,进而求出直角边的长度,据此画图。
【详解】解:设直角边为3x厘米,另一条直角边为2x厘米。
3x×2x÷2=12
6x2÷2×2=12×2
6x2=24
6x2÷6=24÷6
x2=4
x=2
3×2=6(厘米)
3×2=4(厘米)
说明这个三角形的直角边分别为6厘米,4厘米。
(画法不唯一)
【点睛】本题考查了比的应用以及三角形的面积的灵活应用。
23.50立方分米
【分析】根据1升=1立方分米,则45升为45立方分米,已知相同质量的冰和水的体积之比是10∶9,则把冰看作10份,水看作9份,用45÷9即可求出1份是多少,进而求出10份是多少。据此解答。
【详解】45升=45立方分米
45÷9×10
=5×10
=50(立方分米)
答:结成冰后的体积是50立方分米。
【点睛】本题主要考查了比的应用,求出每份的量是多少是解答本题的关键。
24.男队员84名;女队员60名
【分析】男、女队员人数的比是7∶5,男队员人数占7份,女队员人数占5份,男队员比女队员多24名,根据男队员人数比女队员人数多的份数求出每份的量,最后乘男队员人数和女队员人数占的份数,据此解答。
【详解】24÷(7-5)
=24÷2
=12(名)
男队员:12×7=84(名)
女队员:12×5=60(名)
答:男队员有84名,女队员有60名。
【点睛】掌握按比例分配问题的解题方法是解答题目的关键。
25.42人
【分析】由题意可知,书法组的人数原来占两组人数总和的,将书法组的10名同学调到朗诵组去后,书法组的人数原来占两组人数总和的,则这10名学生占两组总人数的(-),根据除法的意义,用10除以(-)即可求出两组的总人数,再根据按比分配的方法求出原来书法组有多少人。
【详解】10÷(-)
=10÷(-)
=10÷
=10×
=72(人)
72×=42(人)
答:原来书法组有42人。
【点睛】本题考查按比分配问题,求出两组原来共有多少人是解题的关键。
26.960千克
【分析】已知苹果与橙子的质量比是3∶5,则把苹果的质量看作3份,橙子的质量看作5份,则苹果比橙子少(5-3)份,又已知运来苹果比橙子少240千克,则用240÷(5-3)即可求出每份是多少,进而求出(3+5)份是多少,也就是水果店运来苹果和橙子一共多少千克。
【详解】240÷(5-3)×(3+5)
=240÷2×8
=120×8
=960(千克)
答:水果店运来苹果和橙子一共960千克。
【点睛】本题主要考查了比的应用,关键是求出每份的量是多少。
27.苹果树150棵;桃树60棵
【分析】由题意可知,苹果树和桃树一共(5+2)份,苹果树的棵数占其中的5份,桃树的棵数占其中的2份,苹果树比桃树多(5-2)份,且苹果树比桃树多90棵,先求出比中每份表示的量,再乘苹果树、桃树占的份数,据此解答。
【详解】90÷(5-2)
=90÷3
=30(棵)
苹果树:30×5=150(棵)
桃树:30×2=60(棵)
答:果园里苹果树150棵,桃树60棵。
【点睛】本题主要考查比的应用,掌握按比例分配问题的解题方法是解答题目的关键。
28.2000尾
【分析】把鱼苗总数看作单位“1”,鲢鱼鱼苗占鱼苗总数的,用乘法计算即可求出鲢鱼的鱼苗应放养多少尾。
【详解】4500×
=4500×
=2000(尾)
答:鲢鱼的鱼苗应放养2000尾。
【点睛】考查比的应用,找准单位“1”,用单位“1”乘对应的分率即可求出对应的量。
29.(1)10小时
(2)
【分析】(1)根据绍兴的白昼与黑夜时间比约是5∶7,一天有24小时,用24小时除以(5+7),再乘5,求出这一天绍兴的白昼时间约是多少小时;
(2)根据绍兴的白昼与黑夜时间比约是5∶7,用24小时除以(5+7),再乘7,求出这一天绍兴的黑夜时间约是多少小时;再根据漠河县的白昼与黑夜时间比约是1∶2,用24小时除以(1+2),再乘2,求出这一天漠河的黑夜时间约是多少小时,最后求一个数是另一个数的几分之几,用除法即可求出。
【详解】(1)24÷(5+7)×5
=24÷12×5
=2×5
=10(小时)
答:“冬至”这一天绍兴的白昼约有10小时。
(2)24÷(5+7)×7
=24÷12×7
=2×7
=14(小时)
24÷(1+2)×2
=24÷3×2
=8×2
=16(小时)
14÷16=
答:绍兴的黑夜时间是漠河黑夜时间的。
【点睛】本题考查了比的应用,解题关键在于,能根据白昼和黑夜的比求出一份时间是多少小时。
30.第一个小时
【分析】根据题意,用560乘求出第一个小时修路长度,用560减去第一个小时修路长度得到剩下的长度,再按照3∶4分配,求出第二小时和第三小时修的长度,找出最长的即可;据此解答。
【详解】560×=210(米)
560-210=350(米)
350÷(3+4)
=350÷7
=50(米)
50×3=150(米)
50×4=200(米)
210米>200米>150米
答:第一个小时修的路最长。
【点睛】此题考查了分数与比的应用,关键能够结合条件求出对应的数量再比较。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
人教版六年级上册第四单元比(知识点梳理+能力百分练)五
知识点梳理
1、比的意义:两个数的比表示两个数相除。
2、比的各部分的名称:从左到右依次是比的前项、比号、比的后项。
3、区分比和比值:比是一个式子,表示两个数的关系,可以写成比的形式,也可以写成分数的形式。比值是一个数,通常用分数表示,也可以用整数或小数表示。
4、比的基本性质:比的前项和后项同时乘或除以相同的数(0除外),比值不变。
5、化简比:根据比的基本性质,可以把比化简成最简单的整数比。
6、按比例分配:把一个量按一定的比例分配的方法叫做按比例分配。
能力百分练
一、选择题(共16分)
1.若a、b是两个非0的自然数,a>b,则(a+b)∶a的比值( )。
A.是0到1之间的数 B.是1到2之间的数
C.有可能是2 D.有可能大于2
2.下列直角三角形,直角边a与直角边b的比不是2∶1的是( )。
A.A B.B C.C D.D
3.把50克蜂蜜加入500克水中,蜂蜜与蜂蜜水的质量比是( )。
A.1∶10 B.1∶11 C.10∶11 D.11∶10
4.小李走的路比小红多,小李走的时间是小红的,那么小李和小红的速度比是( )。
A. B. C. D.
5.一个等腰三角形的周长是120厘米,有两条相邻的边的长度比是2∶1,则这个三角形的底是( )厘米。
A.60 B.48 C.30 D.24
6.声乐社团中,男、女生的人数比是4∶5,下面说法正确的是( )。
A.女生人数是男生人数的 B.男生人数比女生人数少
C.女生人数比男生人数多 D.女生人数占社团总人数的
7.在4∶5中,如果比的后项增加10,要使比值不变,比的前项应( )。
A.乘2 B.乘3 C.增加10 D.减少10
8.小丽和小红从学校去图书馆,小丽需要9分钟,小红需要6分钟。小丽和小红的速度比是( )。
A.9∶6 B.3∶2 C.2∶3 D.∶
二、填空题(共16分)
9.把3.75∶1.8化成最简整数比是( ),比值是( )。
10.工程队挖一条水渠,已经挖了1200m,已经挖的米数与未挖米数的比是3∶5,这条水渠全长( )m。
11.有两堆小麦,甲堆小麦质量的正好等于乙堆质量的。甲乙两堆小麦质量的比是( )∶( )。
12.教室地面的周长是36m,长与宽的比是5∶4。这个教室的地面面积是( )m2。
13.如图,小新家的院子被分成5个形状、大小都相同的长方形,每个长方形的周长是10米,那么院子的周长是( )米。
14.一件衬衣的售价为100元,一条裤子的售价和衬衣的售价之比是;这条裤子的售价为( )元。
15.图书馆上午借出20本书籍,下午借出36本书籍,图书馆上午和下午借出的书籍的本数比是( )(填最简单的整数比),比值是( )。
16.一个等腰三角形,它的顶角与一个底角的度数比是1∶2,这个三角形中最大的内角度数是( )。
三、判断题(共8分)
17.甲数和乙数的比是2∶3,乙数和丙数的比是4∶5,则甲数∶丙数=2∶5。( )
18.上衣比裤子贵,则上衣和裤子的价格比是7∶2。( )
19.一个长方形的周长是36厘米,长和宽的比是2∶1,它的面积是288平方厘米。( )
20.红红和老师今年的年龄比为1∶9,10年后,他们的年龄比不变。( )
四、计算题(共6分)
21.(6分)化简比。
升∶350毫升
五、作图题(共6分)
22.(6分)画一个面积为12平方厘米的直角三角形,要求两条直角边比为3∶2。(每一格边长1厘米)
六、解答题(共48分)
23.(6分)相同质量的冰和水的体积之比是10∶9。现有体积为45升的水,结成冰后的体积是多少立方分米?
24.(6分)学校武术队的男队员比女队员多24名,已知男、女队员人数的比是7∶5,则女队员与男队员各有多少名?
25.(6分)书法组和朗诵组的人数比为7∶5,如果将书法组的10名同学调到朗诵组去,这时书法组和朗诵组的人数比为4∶5,原来书法组有多少人?
26.(6分)水果店运来苹果比橙子少240千克,已知苹果与橙子的质量比是3∶5,水果店运来苹果和橙子一共多少千克?
27.(6分)果园里苹果树比桃树多90棵,苹果树的棵数与桃树的棵数比为5∶2,果园里苹果树、桃树各多少棵?
28.(6分)一只鱼塘按4∶5放养鲢鱼和鲤鱼,一共可以放养4500尾,其中鲢鱼的鱼苗应放养多少尾?
29.(6分)2022年12月22日是“冬至”,是一年中白昼最短、黑夜最长的一天。这天绍兴的白昼与黑夜时间比约是5∶7,而“中国最北端”的漠河县的白昼与黑夜时间比约是1∶2。
(1)“冬至”这一天绍兴的白昼约有几小时?
(2)“冬至”这一天,绍兴的黑夜时间是漠河黑夜时间的几分之几?
30.(6分)工程队正在进行道路抢修,要求三小时修好一条560米的公路,第一个小时修了全长的,第二小时和第三小时修的长度比是3∶4,问:这三小时,哪一小时修的路最长?
参考答案
1.B
【分析】两个不为0的数相除,如果被除数大于除数,则商大于1;根据分数和比的关系,可知(a+b)∶a=,根据分数加法的意义,可得=1+;如果分子小于分母,则分数值小于1,据此解答即可。
【详解】a+b>a
根据比和除法的关系,可知(a+b)∶a的比值一定大于1;
(a+b)∶a
=
=+
=1+
a>b
所以<1
1+<2
据此可知,(a+b)∶a的比值是1到2之间的数。
故答案为:B
【点睛】本题可根据比和分数、除法之间的关系进行解答。
2.A
【分析】两数相除又叫两个数的比,分别数出各三角形直角边格数,写出a与b的比,能化简的化简即可。
【详解】A.2∶4=1∶2
B.4∶2=2∶1
C.2∶1
D.3∶1.5=30∶15=2∶1
故答案为:A
【点睛】关键是理解比的意义,掌握化简比的方法。
3.B
【分析】根据题意,先用蜂蜜的质量加上水的质量,求出蜂蜜水的质量;然后根据比的意义写出蜂蜜与蜂蜜水的质量比,再化简比即可。
【详解】50∶(50+500)
=50∶550
=(50÷50)∶(550÷50)
=1∶11
蜂蜜与蜂蜜水的质量比是1∶11。
故答案为:B
【点睛】本题考查比的意义及化简比。注意化简比的结果是一个比,它的前项和后项都是整数,并且是互质数。
4.A
【分析】小李走的路比小红多,将小红走的路看作4,则小李走的路是(4+1),小李走的时间是小红的,将小红走的时间看作11,则小李走的时间是10,速度=路程÷时间,据此表示出两人走的速度,写出速度比,化简即可。
【详解】小李速度:10÷(4+1)
=10÷5
=2
小红速度:11÷4=
小李和小红的速度比:2∶=(2×4)∶(×4)=8∶11
故答案为:A
【点睛】关键是理解速度、时间、路程之间的关系,理解分数和比的意义。
5.D
【分析】根据三角形三边关系,可以确定这个等腰三角形的3条边的比是2∶2∶1,共(2+2+1)份,求出一份数就是等腰三角形的底。
【详解】120×
=120×
=24(厘米)
则三角形的底是24厘米。
故答案为:D
【点睛】关键是熟悉三角形三边关系和等腰三角形的特征,理解比的意义。
6.B
【分析】把男生的人数看作“4”,则女生人数是“5”,总人数是“(4+5)”。
A.求女生人数是男生人数的几分之几,用女生人数除以男生人数。
B.求男生人数比女生人数少几分之几,用男、女生人数之差除以女生人数。
C.求女生人数比男生人数多几分之几,用男、女生人数之差除以男生人数。
D.求女生人数是社团人数的几分之几,用女生人数除以总人数,据此解答。
【详解】由分析可得:
A.5÷4=,女生人数是男生人数的,选项说法错误;
B.(5-4)÷5
=1÷5
=
男生人数比女生人数少,选项说法正确;
C.(5-4)÷4
=1÷4
=
女生人数比男生人数多,选项说法错误;
D.5÷(4+5)
=5÷9
=
女生人数占社团总人数的,选项说法错误。
故答案为:B
【点睛】求一个数是另一个数的几分之几,用这个数除以另一个数;求一个数比另一个数多或少几分之几,用这两数之差除以另一个数。
7.B
【分析】依据比的性质,即比的前项和后同时乘或除以一个不等于零的数,比的大小不变,即可求解。
【详解】4∶5,比的后项5增加10就变成15,就相当于扩大到原来的15÷5=3倍,
若使比值不变,前项也应扩大到原来的3倍,则变成4×3=12。
故答案为:B
【点睛】解答此题的关键是:看比的前项扩大到原来的几倍,比的后项也扩大相同的倍数,就能保证比值不变。
8.C
【分析】把从学校到图书馆的路程看作单位“1”,根据“路程÷时间=速度”分别求出小丽和小红的速度,进而根据题意求比即可判断。
【详解】(1÷9)∶(1÷6)
=∶
=(×54÷3)∶(×54÷3)
=2∶3
小丽和小红的速度比是2∶3。
故答案为:C
【点睛】解答此题用到的知识点:(1)比的意义;(2)路程、时间和速度三者之间的关系。
9. 25∶12
【分析】第一空根据比的基本性质作答,即比的前项和后项同时乘一个数或除以一个数(0除外)比值不变。第二空用最简整数比中比的前项除以后项即可。
【详解】3.75∶1.8
=(3.75÷0.15)∶(1.8÷0.15)
=25∶12
25∶12
=25÷12
=
即把3.75∶1.8化成最简整数比是25∶12,比值是。
【点睛】此题主要考查了化简比和求比值的方法,另外还要注意化简比的结果是一个比,它的前项和后项都是整数,并且是互质数;而求比值的结果是一个商,可以是整数,小数或分数。
10.3200
【分析】已经挖的米数与未挖米数的比是3∶5,说明已挖的长度是整条水渠长的,用已经挖的长度除以它占全长的分率,求出全长即可。
【详解】(m)
所以这条水渠全长3200m。
【点睛】本题考查按比分配,解答本题的关键是掌握按比分配解题的计算方法。
11. 2 3
【分析】根据“甲堆小麦质量的正好等于乙堆质量的”可得出,甲堆小麦质量×=乙堆质量×,两个乘法算式的积相等,可以设它们积都等于1;
然后根据“因数=积÷另一个因数”,分别求出甲堆小麦质量、乙堆小麦质量的值;
再根据比的意义,写出甲乙两堆小麦质量的比,并根据比的基本性质化简比。
【详解】设甲堆小麦质量×=乙堆质量×=1;
甲堆小麦质量=1÷=1×=
乙堆质量=1÷=1×4=4
甲堆小麦质量∶乙堆质量
=∶4
=(×3)∶(4×3)
=8∶12
=(8÷4)∶(12÷4)
=2∶3
甲乙两堆小麦质量的比是2∶3。
【点睛】运用赋值法,根据乘法中各部分的关系计算出甲堆小麦质量、乙堆小麦质量的值,再根据比的意义和比的化简解答。
12.80
【分析】根据长方形的周长公式:C=2(a+b),用36除以2即可求出该长方形的长与宽的和,再根据按比分配问题,求出长方形的长和宽的值,最后根据长方形的面积公式:S=ab,据此计算即可。
【详解】36÷2=18(m)
18÷(5+4)
=18÷9
=2(m)
2×5=10(m)
2×4=8(m)
10×8=80(m2)
则这个教室的地面面积是80m2。
【点睛】本题考查按比分配问题,结合长方形的周长和面积的计算方法是解题的关键。
13.22
【分析】已知每个小长方形的周长是10米,根据长方形的长、宽之和=周长÷2,求出小长方形长、宽的和;
从图中可知,2个小长方形的长等于3个小长方形的宽,则小长方形的长、宽之比是3∶2,即长、宽各占长、宽之和的、,根据求一个数的几分之几是多少,用乘法分别求出小长方形的长和宽;
从图中可知,院子的长等于小长方形长的2倍,院子的宽等于小长方形的长加宽,由此求出院子的长和宽,然后根据长方形的周长=(长+宽)×2,代入数据计算,即可求出这个院子的周长。
【详解】小长方形的长、宽之比是3∶2;
小长方形的长、宽之和:10÷2=5(米)
长:5×=3(米)
宽:5×=2(米)
院子的长:3×2=6(米)
院子的宽:3+2=5(米)
院子的周长:
(6+5)×2
=11×2
=22(米)
院子的周长是22米。
【点睛】本题考查按比分配问题以及长方形周长公式的灵活运用,从图中找出小长方形的长、宽之比,然后把比转化成分数,根据分数乘法的意义求出每个小长方形的长、宽是解题的关键。
14.150
【分析】已知两个数量的比和其中的一个数量,求另外一个数量的解题方法:已知量÷对应的份数=每份的量,每份量×相应份数=对应的量。此题中100元对应2份,用100÷2先求出每份的钱数,再用每份的钱数乘3求出这条裤子的售价。
【详解】100÷2×3
=50×3
=150(元)
所以这条裤子的售价为150元。
【点睛】解按比分配的问题时,一定要注意已知量所对应的份数是多少。
15. 5∶9
【分析】根据比的意义,写出图书馆上午和下午借出的书籍的本数比,再根据比的基本性质,比的前项和后项同时乘一个数或除以一个数(0除外)化简比;最后用比的前项除以后项即可。
【详解】20∶36
=(20÷4)∶(36÷4)
=5∶9
图书馆上午和下午借出的书籍的本数比是5∶9;
5∶9
=5÷9
=
比值是。
【点睛】此题主要考查了化简比和求比值的方法,另外还要注意化简比的结果是一个比,它的前项和后项都是整数,并且是互质数;而求比值的结果是一个商,可以是整数,小数或分数。
16.72度/72°
【分析】根据等腰三角形的特征,可知两个底角相等,可知三个角度的比是1∶2∶2,把三角形的三个内角分别看作1份、2份和2份,已知三角形的内角和是180度,用180÷(1+2+2)即可求出每份是多少,进而求出2份是多少,也就是最大的内角度数。
【详解】180÷(1+2+2)
=180÷5
=36(度)
36×2=72(度)
这个三角形中最大的内角度数是72度。
【点睛】本题考查了比的应用,明确三角形内角和是180度以及等腰三角形的特征是解题的关键。
17.×
【分析】根据比的基本性质,比的前项和后项同时乘或除以一个不为0的数,比值不变,据此化为三联比即可求解。
【详解】甲数∶乙数=2∶3=8∶12
乙数∶丙数=4∶5=12∶15
可得甲数∶乙数∶丙数=8∶12∶15
所以甲数∶丙数=8∶15。
故答案为:×
【点睛】本题考查比的性质,熟练运用比的基本性质是解题的关键。
18.×
【分析】假设裤子为100元,根据题意可知,上衣比裤子贵,把裤子的价格看作单位“1”,上衣的价格是裤子的(1+),根据分数乘法的意义,用100×(1+)即可求出上衣的价格,最后写出上衣和裤子的价格比,再化简即可,化简比根据比的基本性质作答,即比的前项和后项同时乘或除以一个数(0除外),比值不变。据此解答。
【详解】假设裤子为100元,
上衣:100×(1+)
=100×
=140(元)
140∶100
=(140÷20)∶(100÷20)
=7∶5
上衣比裤子贵,则上衣和裤子的价格比是7∶5。原题干说法错误。
故答案为:×
【点睛】本题考查了分数和比的关系的转化,可用假设法解决问题。
19.×
【分析】根据长方形的周长=(长+宽)×2,已知长方形的周长是36厘米,则用36÷2即可求出长与宽的和,又已知长和宽的比是2∶1,把长看作2份,宽看作1份,用36÷2÷(2+1)即可求出每份是多少,进而求出长和宽,最后根据长方形的面积公式求解即可。
【详解】36÷2÷(2+1)
=18÷3
=6(厘米)
6×2=12(厘米)
6×1=6(厘米)
12×6=72(平方厘米)
即它的面积是72平方厘米。
故答案为:×
【点睛】本题主要考查了按比分配问题,熟记长方形周长公式和面积公式是解题的关键。
20.×
【分析】比的前项和后项,同时乘或除以相同的数(0除外),比值不变,据此分析。
【详解】红红和老师今年的年龄比为1∶9,10年后,相当于年龄比的前项和后项同时加上10,年龄比会改变,所以原题说法错误。
故答案为:×
【点睛】关键是掌握并灵活运用比的基本性质。
21.8∶9;4∶1;5∶7
【分析】(1)根据比的基本性质比的前项和后项同时乘3和4的最小公倍数12。
(2)根据比的基本性质比的前项和后项同时乘100,把小数比转化为整数比128∶32;再把整数比的前项和后项同时除以128和32的最大公因数32。
(3)先把升换算为250毫升;再把比的前项和后项同时除以250和350的最大公因数50。
【详解】
=
=8∶9
=
=128∶32
=(128÷32)∶(32÷32)
=4∶1
升∶350毫升
=250毫升∶350毫升
=250∶350
=(250÷50)∶(350÷50)
=5∶7
22.见详解
【分析】因为三角形是一个直角三角形,则三角形的两条直角边相当于三角形的底和高,又已知三角形的面积为12平方厘米,两条直角边比为3∶2,设直角边为3x厘米,另一条直角边为2x厘米,根据三角形的面积公式可得,3x×2x÷2=12,据此求出x=4,进而求出直角边的长度,据此画图。
【详解】解:设直角边为3x厘米,另一条直角边为2x厘米。
3x×2x÷2=12
6x2÷2×2=12×2
6x2=24
6x2÷6=24÷6
x2=4
x=2
3×2=6(厘米)
3×2=4(厘米)
说明这个三角形的直角边分别为6厘米,4厘米。
(画法不唯一)
【点睛】本题考查了比的应用以及三角形的面积的灵活应用。
23.50立方分米
【分析】根据1升=1立方分米,则45升为45立方分米,已知相同质量的冰和水的体积之比是10∶9,则把冰看作10份,水看作9份,用45÷9即可求出1份是多少,进而求出10份是多少。据此解答。
【详解】45升=45立方分米
45÷9×10
=5×10
=50(立方分米)
答:结成冰后的体积是50立方分米。
【点睛】本题主要考查了比的应用,求出每份的量是多少是解答本题的关键。
24.男队员84名;女队员60名
【分析】男、女队员人数的比是7∶5,男队员人数占7份,女队员人数占5份,男队员比女队员多24名,根据男队员人数比女队员人数多的份数求出每份的量,最后乘男队员人数和女队员人数占的份数,据此解答。
【详解】24÷(7-5)
=24÷2
=12(名)
男队员:12×7=84(名)
女队员:12×5=60(名)
答:男队员有84名,女队员有60名。
【点睛】掌握按比例分配问题的解题方法是解答题目的关键。
25.42人
【分析】由题意可知,书法组的人数原来占两组人数总和的,将书法组的10名同学调到朗诵组去后,书法组的人数原来占两组人数总和的,则这10名学生占两组总人数的(-),根据除法的意义,用10除以(-)即可求出两组的总人数,再根据按比分配的方法求出原来书法组有多少人。
【详解】10÷(-)
=10÷(-)
=10÷
=10×
=72(人)
72×=42(人)
答:原来书法组有42人。
【点睛】本题考查按比分配问题,求出两组原来共有多少人是解题的关键。
26.960千克
【分析】已知苹果与橙子的质量比是3∶5,则把苹果的质量看作3份,橙子的质量看作5份,则苹果比橙子少(5-3)份,又已知运来苹果比橙子少240千克,则用240÷(5-3)即可求出每份是多少,进而求出(3+5)份是多少,也就是水果店运来苹果和橙子一共多少千克。
【详解】240÷(5-3)×(3+5)
=240÷2×8
=120×8
=960(千克)
答:水果店运来苹果和橙子一共960千克。
【点睛】本题主要考查了比的应用,关键是求出每份的量是多少。
27.苹果树150棵;桃树60棵
【分析】由题意可知,苹果树和桃树一共(5+2)份,苹果树的棵数占其中的5份,桃树的棵数占其中的2份,苹果树比桃树多(5-2)份,且苹果树比桃树多90棵,先求出比中每份表示的量,再乘苹果树、桃树占的份数,据此解答。
【详解】90÷(5-2)
=90÷3
=30(棵)
苹果树:30×5=150(棵)
桃树:30×2=60(棵)
答:果园里苹果树150棵,桃树60棵。
【点睛】本题主要考查比的应用,掌握按比例分配问题的解题方法是解答题目的关键。
28.2000尾
【分析】把鱼苗总数看作单位“1”,鲢鱼鱼苗占鱼苗总数的,用乘法计算即可求出鲢鱼的鱼苗应放养多少尾。
【详解】4500×
=4500×
=2000(尾)
答:鲢鱼的鱼苗应放养2000尾。
【点睛】考查比的应用,找准单位“1”,用单位“1”乘对应的分率即可求出对应的量。
29.(1)10小时
(2)
【分析】(1)根据绍兴的白昼与黑夜时间比约是5∶7,一天有24小时,用24小时除以(5+7),再乘5,求出这一天绍兴的白昼时间约是多少小时;
(2)根据绍兴的白昼与黑夜时间比约是5∶7,用24小时除以(5+7),再乘7,求出这一天绍兴的黑夜时间约是多少小时;再根据漠河县的白昼与黑夜时间比约是1∶2,用24小时除以(1+2),再乘2,求出这一天漠河的黑夜时间约是多少小时,最后求一个数是另一个数的几分之几,用除法即可求出。
【详解】(1)24÷(5+7)×5
=24÷12×5
=2×5
=10(小时)
答:“冬至”这一天绍兴的白昼约有10小时。
(2)24÷(5+7)×7
=24÷12×7
=2×7
=14(小时)
24÷(1+2)×2
=24÷3×2
=8×2
=16(小时)
14÷16=
答:绍兴的黑夜时间是漠河黑夜时间的。
【点睛】本题考查了比的应用,解题关键在于,能根据白昼和黑夜的比求出一份时间是多少小时。
30.第一个小时
【分析】根据题意,用560乘求出第一个小时修路长度,用560减去第一个小时修路长度得到剩下的长度,再按照3∶4分配,求出第二小时和第三小时修的长度,找出最长的即可;据此解答。
【详解】560×=210(米)
560-210=350(米)
350÷(3+4)
=350÷7
=50(米)
50×3=150(米)
50×4=200(米)
210米>200米>150米
答:第一个小时修的路最长。
【点睛】此题考查了分数与比的应用,关键能够结合条件求出对应的数量再比较。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
