人教版六年级数学上册第五单元圆同步学案(知识点梳理+能力百分练)一
文档属性
| 名称 | 人教版六年级数学上册第五单元圆同步学案(知识点梳理+能力百分练)一 |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-25 05:29:17 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版六年级数学上册第五单元圆(知识点梳理+能力百分练)一
知识点梳理
1、圆的定义:圆是由曲线围成的一种平面图形。
2、圆心:将一张圆形纸片对折两次,折痕相交于圆中心的一点,这一点叫做圆心,一般用字母О表示,它到圆上任意一点的距离都相等;
半径:连接圆心到圆上任意一点的线段叫做半径,一般用字母r表示,把圆规两脚分开,两脚之间的距离就是圆的半径;
直径:通过圆心并且两端都在圆上的线段叫做直径,一般用字母d表示,直径是一个圆内最长的线段。
圆心确定圆的位置,半径确定圆的大小。在同圆或等圆内,有无数条半径,有无数条直径。所有的半径都相等,所有的直径都相等。直径的长度是半径的2倍。
3、圆规画圆的步骤:(1)把圆规的两只脚分开,定好两只脚之间的距离;(2)把带针尖的脚固定在一个点上;(3)把装铅笔的脚绕着这个点旋转1圈,就画出了一个圆。
4、圆的周长:围成圆的曲线的长度叫做圆的周长。用字母C表示。任意一个圆的周长与它的直径的比值都是一个固定的数﹐我们把它叫做圆周率,用字母r表示。圆的周长计算公式C=Πd=2Πr。
5、圆的面积:圆所占平面的大小叫做圆的面积。用字母S表示。圆的面积计算公式:S=Πr2。
6、环形的面积:S环=Π(R2 -r2)
7、圆上任意两点之间的部分叫做弧。
8、扇形:一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。在扇形中,顶点在圆心的角叫做圆心角。
能力百分练
一、选择题(共16分)
1.小安在纸上画了两个大小不同的圆,比较这两个圆,( )是相同的。
A.圆周率 B.周长 C.半径 D.面积
2.小东想在空地上围出一块面积为706.5平方米的圆形土地来种菜他应该用多长的篱笆来围(圆周率取3.14)。( )
A.78.5米 B.87.5米 C.92.4米 D.94.2米
3.约2000年前,中国古代数学著作《周髀算经》中就有“周三径一”的说法,意思是说圆的周长约是它的直径的3倍。如果线段AF表示一个圆的周长,那么这个圆的直径可能是线段( )的长。
A.AB B.AD C.CE D.CF
4.观察下图的正方形、圆形、正六边形,下面的想法错误的是( )。
A.圆周长是正方形周长与正六边形周长和的一半
B.正方形周长是圆直径的4倍
C.圆周长比直径的3倍多,比圆的直径4倍少
5.一个周长为25.12cm的圆,直径减少2cm后,面积减少了( )cm2。
A.9.42 B.21.98 C.37.68 D.87.92
6.如图,有一个直径是6厘米的圆在一个宽是6厘米的长方形方框(厚度不计)内平移。这个圆不能覆盖部分的面积是( )平方厘米。
A.7.74 B.15.48 C.28.26 D.36
7.如图,中间是面积为16平方厘米的正方形,与这个正方形每一条边相连的都是圆心角为90°的扇形。那么涂色部分的面积是( )平方厘米。
A.π×12 B.π×22 C.π×42 D.π×62
8.下面三个正方形的边长都是4厘米,三个正方形中阴影部分的面积相比较,( )。
A.图①最大 B.图②最大 C.图③最大 D.同样大
二、填空题(共16分)
9.大圆的半径等于小圆的直径,大圆与小圆的面积之和是80平方厘米,那么大圆的面积是( )平方厘米。
10.如图,把一个圆平均分成若干份,再拼成一个近似的长方形。这个长方形的长与宽的比是( ); 如果这个长方形的长是9.42厘米,那么这个圆的面积是( )平方厘米。
11.如下图,将圆周12等分,那么A点在O点的( )方向,距离( )千米。
12.求阴影部分面积(长度单位:厘米),阴影部分面积是( )平方厘米。
13.小明用圆规画一个圆,圆规两脚张开的距离是3厘米,画出的圆的周长是( )厘米,面积是( )平方厘米。
14.一个边长是2厘米的正方形和一个圆组合在一起,形成了一个新的组合图形(如右上图),两个图形重合部分的面积是正方形面积的( )%。
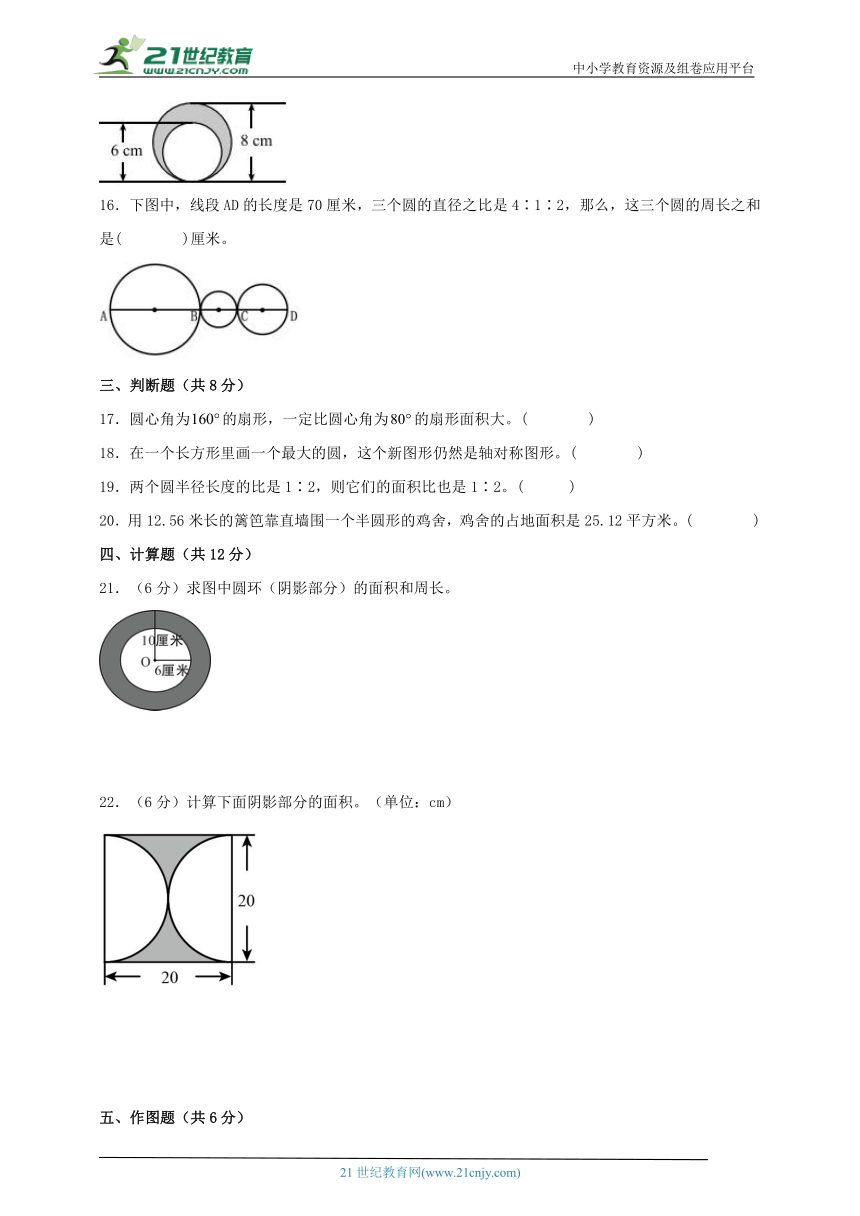
15.如图中两个圆的直径分别是8厘米和6厘米,阴影部分的面积是( )平方厘米。
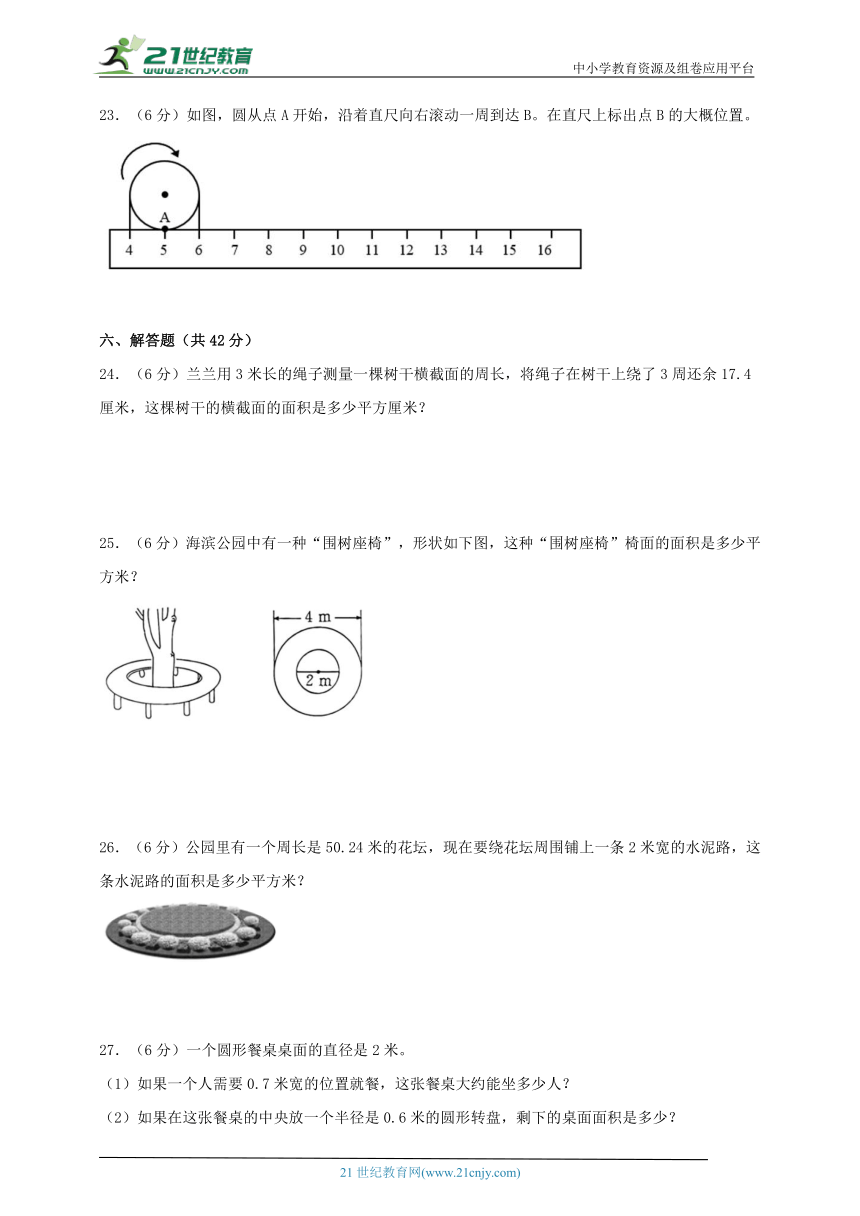
16.下图中,线段AD的长度是70厘米,三个圆的直径之比是4∶1∶2,那么,这三个圆的周长之和是( )厘米。
三、判断题(共8分)
17.圆心角为的扇形,一定比圆心角为的扇形面积大。( )
18.在一个长方形里画一个最大的圆,这个新图形仍然是轴对称图形。( )
19.两个圆半径长度的比是1∶2,则它们的面积比也是1∶2。( )
20.用12.56米长的篱笆靠直墙围一个半圆形的鸡舍,鸡舍的占地面积是25.12平方米。( )
四、计算题(共12分)
21.(6分)求图中圆环(阴影部分)的面积和周长。
22.(6分)计算下面阴影部分的面积。(单位:cm)
五、作图题(共6分)
23.(6分)如图,圆从点A开始,沿着直尺向右滚动一周到达B。在直尺上标出点B的大概位置。
六、解答题(共42分)
24.(6分)兰兰用3米长的绳子测量一棵树干横截面的周长,将绳子在树干上绕了3周还余17.4厘米,这棵树干的横截面的面积是多少平方厘米?
25.(6分)海滨公园中有一种“围树座椅”,形状如下图,这种“围树座椅”椅面的面积是多少平方米?
26.(6分)公园里有一个周长是50.24米的花坛,现在要绕花坛周围铺上一条2米宽的水泥路,这条水泥路的面积是多少平方米?
27.(6分)一个圆形餐桌桌面的直径是2米。
(1)如果一个人需要0.7米宽的位置就餐,这张餐桌大约能坐多少人?
(2)如果在这张餐桌的中央放一个半径是0.6米的圆形转盘,剩下的桌面面积是多少?
28.(6分)一张长方形纸,长是20厘米,宽是12厘米,小红用这张长方形纸,剪去一个最大的圆,剩下的边角料的面积是多少平方厘米?
29.(6分)观察下图,按照要求提出数学问题,并解答。
(1)用两步计算的问题:________________________________________
(2)用四步或四步以上计算的问题:_________________________________
30.(6分)李阿姨靠墙围了一个半圆形的菜园,半径是4米(如图)。
(1)围这个菜园需要多长的篱笆?
(2)如果要扩大这个菜园,把它的直径增加2米,菜园的面积增加了多少平方米?
参考答案
1.A
【分析】圆的周长与直径的比是个定值,也就是圆周率,圆的半径大小决定了圆的大小,也决定了圆面积的大小。
【详解】A.圆的周长与直径的比是个定值,也就是圆周率,所以A正确;
B.圆的大小不一样,所以周长不一样,所以B错误;
C.圆的大小不一样,所以半径不一样,所以C错误;
D.圆的大小不一样,所以面积不一样,所以D错误。
故答案为:A
【点睛】考查圆的特点,重点对圆的半径、面积、周长以及圆周率有深刻的理解和认识。
2.D
【分析】先根据圆的面积公式:S=,代入数据求出这块圆形菜地的半径,再根据圆的周长公式:C=,代入半径的数据,即可求出篱笆的长度。
【详解】r2=706.5÷3.14=225
因为15×15=225,
所以圆的半径为15米。
2×3.14×15=94.2(米)
即他应该用94.2米长篱笆来围。
故答案为:D
【点睛】此题的解题关键是灵活运用圆的周长和圆的面积公式求解。
3.C
【分析】由题意可知,圆的周长大约是它直径的3倍,则圆的直径大约占周长的,线段AF表示圆的周长,把AF平均分成3份,圆的直径约占其中的1份,据此解答。
【详解】由图可知,线段AC的长度大约占线段AF长度的,线段AB的长度小于线段AC的长度,线段AD和线段CF的长度大于线段AC的长度,线段CE和线段AC的长度基本相同,所以这个圆的直径可能是线段CE的长。
故答案为:C
【点睛】本题主要考查圆的周长与直径的关系,明确圆的直径大约占它周长的是解答题目的关键。
4.A
【分析】A.圆的直径=正方形边长,圆的半径=正六边形边长,圆的周长=πd,正方形周长=边长×4,正六边形周长=边长×6,据此直接计算即可;
B.圆的直径=正方形边长,正方形周长=边长×4,据此分析;
C.圆的周长=πd,据此分析。
【详解】假设正方形边长是4。
A.圆的周长=3.14×4=12.56
(4×4+4÷2×6)÷2
=(16+12)÷2
=28÷2
=14
圆的周长是12.56,正方形周长与正六边形周长和的一半是14,选项说法错误。
B.正方形周长=边长×4=圆的直径×4,选项说法正确。
C.圆的周长=πd,π一般取值3.14,圆周长比直径的3倍多,比圆的直径4倍少,说法正确。
故答案为:A
【点睛】关键是理解圆、正方形、正六边形之间的关系,掌握并灵活运用正方形和圆的周长公式。
5.B
【分析】先根据“”求出原来圆的直径,再求出现在圆的直径,最后根据“”表示出原来和现在圆的面积,并求出它们的差,据此解答。
【详解】25.12÷3.14=8(cm)
8-2=6(cm)
3.14×(8÷2)2-3.14×(6÷2)2
=3.14×16-3.14×9
=3.14×(16-9)
=3.14×7
=21.98(cm2)
所以,面积减少了21.98cm2。
故答案为:B
【点睛】熟练掌握圆的周长和面积的计算公式是解答题目的关键。
6.A
【分析】如图所示,这个圆不能覆盖的面积是1、2、3、4四部分的面积,把3和4向左平移至3’和4’的位置,这个圆不能覆盖部分的面积=正方形的面积-圆的面积,据此解答。
【详解】6×6-3.14×(6÷2)2
=6×6-3.14×9
=36-28.26
=7.74(平方厘米)
所以,这个圆不能覆盖部分的面积是7.74平方厘米。
故答案为:A
【点睛】准确找出这个圆不能覆盖部分的面积,并把该面积转化为正方形的面积和圆的面积的差是解答题目的关键。
7.C
【分析】根据题意可知,4个扇形可以组成一个圆,圆的半径是正方形的边长,已知正方形的面积是16平方厘米,根据圆面积公式:S=πr2,正方形的面积=边长×边长,可推出半径是4厘米,所以用π×42即可求出4个扇形的面积,阴影部分的面积占4个扇形面积的;用π×42即可求出阴影部分的面积。据此解答。
【详解】16=4×4
扇形的半径是4厘米,
π×42
=π×16
=12π(平方厘米)
涂色部分的面积是12π平方厘米,列式为π×42。
故答案为:C
【点睛】本题主要考查了圆面积公式的灵活应用以及分数乘法的应用,要熟练掌握公式。
8.D
【分析】利用圆的面积公式:S=r2,分别计算各阴影部分的面积,比较即可得出结论。
【详解】图①:3.14×42÷4
=3.14×4×(4÷4)
=3.14×4
=12.56(平方厘米)
图②:3.14×(4÷2)2
=3.14×4
=12.56(平方厘米)
图③:3.14×(4÷2÷2)2×4
=3.14×4
=12.56(平方厘米)
所以三个图形的阴影部分面积相等。
故答案为:D
【点睛】本题主要考查阴影部分的面积,关键利用圆的面积公式计算。
9.64
【分析】根据题意可知,设小圆的半径是x厘米,则大圆的半径是2x厘米,根据圆面积公式,π×2x×2x+π×x2=80,然后求出πx2的值,进而乘4即可求出大圆的面积。
【详解】解:设小圆的半径是x厘米,则大圆的半径是2x厘米。
π×2x×2x+π×x2=80
4πx2+πx2=80
5πx2=80
πx2=80÷5
πx2=16
4πx2
=16×4
=64(平方厘米)
大圆的面积是64平方厘米。
【点睛】本题主要考查了圆面积公式的灵活应用,明确大圆半径和小圆半径之间的关系是解答本题的关键。
10. π∶1 28.26
【分析】由圆的面积推导过程可知:将圆拼成近似的长方形后,长方形的长就等于圆的周长的一半,宽就等于圆的半径,根据圆周长公式:C=2πr,可知圆的周长的一半表示为πr,据此写出这个长方形的长与宽的比,再化简即可;如果这个长方形的长是9.42厘米,则圆的周长是(9.42×2)厘米,根据圆周长公式:C=2πr,用周长÷2÷3.14即可求出圆的半径;最后根据圆面积公式:S=πr2,代入数据解答即可。
【详解】这个长方形的长与宽的比:
πr∶r
=(πr÷r)∶(r÷r)
=π∶1
半径:9.42×2÷2÷3.14=3(厘米)
3.14×32
=3.14×9
=28.26(平方厘米)
把一个圆平均分成若干份,再拼成一个近似的长方形。这个长方形的长与宽的比是π∶1; 如果这个长方形的长是9.42厘米,那么这个圆的面积是28.26平方厘米。
【点睛】本题主要考查了圆周长公式、圆面积公式的灵活应用以及比的化简,解答此题的主要依据是圆的面积推导过程。
11. 东偏北60° 40
【分析】如下图,连接OA,周角是360°,将圆周12等分,所以∠BOA=360°÷12×2=。即A点在O点的东偏北(或北偏东)方向。1个单位长度是10千米,OB是4个单位长度,因为OA、OB都是圆的半径,所以OA=OB,即OA也是4个单位长度。
【详解】如上图,
∠BOA=360°÷12×2=60°,10×4=40(千米)。所以A点在O点的东偏北60°(或北偏东30°)方向,距离是40千米。
【点睛】此题考查了周角的度数、圆心角的度数的求法、根据方向和距离确定物体的位置。
12.37.68
【分析】根据圆环的面积公式:S=π(R2-r2),求出阴影部分的面积即可。
【详解】3.14×(42-22)
=3.14×(16-4)
=3.14×12
=37.68(平方厘米)
阴影部分面积是37.68平方厘米。
【点睛】本题考查的是圆环的面积公式的应用,明确大圆和小圆的半径是解题的关键。
13. 18.84 28.26
【分析】圆规两脚张开的距离是圆的半径,即=3厘米。圆的周长,圆的面积,把半径3厘米分别代入圆的周长公式、面积公式计算即可。
【详解】2×3.14×3
=2×3×3.14
=6×3.14
=18.84(厘米)
3.14×32
=3.14×9
=28.26(平方厘米)
所以画出的圆的周长是18.84厘米,面积是28.26平方厘米。
【点睛】在计算圆的面积时,不要把当成计算,应是。
14.78.5
【分析】已知正方形的边长是2厘米,根据正方形的面积公式S=a2,求出正方形的面积;
从图中可知,圆的半径等于正方形的边长;根据圆的面积公式S=πr2,求出圆的面积,再乘,即是两个图形重合部分的面积;
然后用两个图形重合部分的面积除以正方形面积,求出重合部分的面积是正方形面积的百分之几。
【详解】正方形的面积:
2×2=4(平方厘米)
两个图形重合部分的面积:
3.14×22×
=3.14×4×
=3.14(平方厘米)
3.14÷4×100%
=0.785×100%
=78.5%
两个图形重合部分的面积是正方形面积的78.5%。
【点睛】本题考查正方形的面积、圆的面积公式的运用,明确根据求一个数是另一个数的百分之几,用除法计算。
15.21.98
【分析】观察图形可知,阴影部分的面积=大圆的面积-小圆的面积,根据圆的面积公式S=πr2,代入数据计算即可求解。
【详解】3.14×(8÷2)2-3.14×(6÷2)2
=3.14×16-3.14×9
=50.24-28.26
=21.98(平方厘米)
阴影部分的面积是21.98平方厘米。
【点睛】本题考查圆的面积公式的运用,关键是观察图形,分析出阴影部分的面积是由哪些图形面积相减得到,再根据图形的面积公式列式计算。
16.219.8
【分析】把根据圆周长公式:C=πd,可知三个圆的周长和=3.14×AB+3.14×BC+3.14×CD,根据乘法分配律,可知三个圆的周长和=3.14×(AB+BC+CD)=3.14×AD,据此用3.14×70即可求出三个圆的周长和。
【详解】3.14×70=219.8(厘米)
这三个圆的周长之和是219.8厘米。
【点睛】本题主要考查了圆周长公式的灵活应用以及比的应用,这里可以应用圆的周长公式计算,比计算出每个直径的长度更简便。
17.×
【分析】计算扇形面积需要知道半径的大小和圆心角,只知道圆心角而不知道半径,则无法计算扇形的面积,也就无法比较大小。
【详解】计算扇形面积需要知道圆心角和半径,不知道半径的大小,就无法计算面积,也就不能比较面积大小了;所以原题说法错误。
故答案为:×
【点睛】此题主要考查扇形面积的计算方法,注意扇形的面积的大小是由圆心角的度数和半径的大小决定的。
18.√
【分析】如果一个平面图形沿着一条直线对折后,直线两侧的部分能够完全重合,那么这个图形就叫作轴对称图形,这条直线就叫作这个图形的对称轴。长方形是轴对称图形,有2条对称轴;圆是轴对称图形,有无数条对称轴。如下图,
、。
先根据题意画出图形,再根据轴对称的意义判断即可。
【详解】在一个长方形里画一个最大的圆,圆的直径等于长方形的宽。如下图,得到的新图形仍然是轴对称图形,有1条或2条对称轴。原题说法正确。
、
故答案为:√
【点睛】判断组合图形是不是轴对称图形时,要把这些图形看作一个整体,尝试从不同的位置对折。
19.×
【分析】圆的面积,所以圆的面积之比等于圆半径的平方之比,据此判断即可。
【详解】两个圆半径长度的比是1∶2,则它们的面积比是,本题说法错误;
故答案为:×。
【点睛】本题考查比、圆的面积,解答本题的关键是掌握比的意义。
20.√
【分析】由题意可知,篱笆的长度就是整圆周长的一半,据此求出圆的半径,再根据圆的面积公式:S=πr2,据此求出整圆的面积,再除以2就是鸡舍的占地面积。
【详解】12.56÷3.14=4(米)
3.14×42÷2
=3.14×16÷2
=50.24÷2
=25.12(平方米)
则鸡舍的占地面积是25.12平方米。原题干说法正确。
故答案为:√
【点睛】本题考查圆的周长和面积,熟记公式是解题的关键。
21.200.96平方厘米;100.48厘米
【分析】由图可知,大圆的半径为10厘米,小圆的半径为6厘米,利用“”求出圆环的面积;圆环的周长=大圆的周长+小圆的周长,利用“”求出圆环的周长,据此解答。
【详解】面积:3.14×(102-62)
=3.14×(100-36)
=3.14×64
=200.96(平方厘米)
周长:2×3.14×10+2×3.14×6
=2×3.14×(10+6)
=2×3.14×16
=6.28×16
=100.48(厘米)
所以,圆环的面积是200.96平方厘米,圆环的周长是100.48厘米。
22.86cm2
【分析】阴影部分的面积=正方形面积-圆的面积,正方形面积=边长×边长,圆的面积=πr2,据此列式计算。
【详解】20×20-3.14×(20÷2)2
=400-3.14×102
=400-3.14×100
=400-314
=86(cm2)
23.见详解
【分析】圆的周长=πd,点A在刻度5,点A所在刻度+圆的周长=点B所在刻度,据此分析。
【详解】3.14×2=6.28
5+6.28=11.28
【点睛】关键是掌握并灵活运用圆的周长公式。
24.706.5平方厘米
【分析】先用绳子的长减去17.4厘米,再除以3求出树干横截面的周长;由圆的周长可推导出,据此根据圆的周长求出圆的半径;最后利用圆的面积求出这棵树干的横截面的面积。
【详解】3米=300厘米
(300-17.4)÷3
=282.6÷3
=94.2(厘米)
94.2÷3.14÷2
=30÷2
=15(厘米)
3.14×152
=3.14×225
=706.5(平方厘米)
答:这棵树干的横截面的面积是706.5平方厘米。
【点睛】此题考查了圆的周长、圆的面积计算公式。在计算圆的面积时,不要把当成计算,应是。
25.9.42平方米
【分析】观察图形可知,这种“围树座椅”椅面的面积就是圆环的面积,根据圆环的面积公式:S=π(R2-r2),据此计算即可。
【详解】3.14×[(4÷2)2-(2÷2)2]
=3.14×[22-12]
=3.14×[4-1]
=3.14×3
=9.42(平方米)
答:这种“围树座椅”椅面的面积是9.42平方米。
【点睛】本题考查圆环的面积,熟记公式是解题的关键。
26.113.04平方米
【分析】水泥路的形状是个圆环,根据圆的半径=周长÷π÷2,先求出花坛半径,即小圆半径,小圆半径+路宽=大圆半径,确定大圆和小圆半径,根据圆环面积=π(R2-r2),列式解答即可。
【详解】50.24÷3.14÷2=8(米)
8+2=10(米)
3.14×(102-82)
=3.14×(100-64)
=3.14×36
=113.04(平方米)
答:这条水泥路的面积是113.04平方米。
【点睛】关键是掌握并灵活运用圆的周长和圆环面积公式。
27.(1)9人;(2)2.0096平方米
【分析】(1)根据圆的周长=πd,求出餐桌周长,餐桌周长÷一个人需要的长度=坐的人数,结果用四舍五入法保留整数即可。
(2)剩下的面积是个圆环,确定大圆和小圆的半径,根据圆环面积=π(R2-r2),列式解答即可。
【详解】(1)
(人
答:这张餐桌大约能坐9人。
(2)(米)
(平方米)
答:剩下的桌面面积是2.0096平方米。
【点睛】关键是掌握并灵活运用圆的周长和圆环面积公式。
28.126.96平方厘米
【分析】根据题意,可得最大的圆的直径是长方形的宽;然后用12除以2,求出圆的半径,进而求出圆的面积;最后用长方形的面积减去圆的面积,求出剩下的边角料的面积是多少平方厘米即可。
【详解】根据题意,可得最大的圆的直径是长方形的宽
即圆的直径是12厘米
20×12-3.14×(12÷2)2
=240-3.14×36
=240-113.04
=126.96(平方厘米)
答:剩下的边角料的面积是126.96平方厘米。
【点睛】解答此题的关键是熟练掌握长方形和圆的面积的求法。
29.(1)正方形的周长是多少厘米?16厘米;(2)阴影部分的面积是多少平方厘米?3.44平方厘米
【分析】问题合理即可,没有固定答案。例如:
(1)正方形的周长是多少厘米?正方形的边长相当于圆的直径,则用2×2×4即可求正方形周长。
(2)阴影部分的面积是多少平方厘米?根据正方形面积公式和圆面积公式求出正方形的面积和圆面积,然后求出它们的差即可。
【详解】(1)正方形的周长是多少厘米?
直径:2×2=4(厘米)
周长:4×4=16(厘米)
答:正方形的周长是16厘米。(答案不唯一)
(2)阴影部分的面积是多少平方厘米?
4×4 3.14×22
=4×4 3.14×4
=16 12.56
=3.44(平方厘米)
答:阴影部分的面积是3.44平方厘米。(答案不唯一)
【点睛】本题主要考查组合图形的面积,关键利用规则图形的面积公式计算。
30.(1)12.56米
(2)14.13平方米
【分析】(1)根据题意,篱笆是圆周长的一半,用公式:圆周长的一半=πr,将数据代入计算即可;
(2)直径增加2米,也就是半径增加1米,用公式:半圆的面积=πr2÷2,计算出原来菜园的面积与新的面积相减即可得出新增加了多少平方米。
【详解】(1)4×3.14=12.56(米)
答:围这个菜园需要12.56米的篱笆。
(2)2÷2=1(米)
4+1=5(米)
5×5×3.14÷2-4×4×3.14÷2
=25×3.14÷2-16×3.14÷2
=78.5÷2-50.24÷2
=39.25-25.12
=14.13(平方米)
答:菜园的面积增加了14.13平方米。
【点睛】此题考查了圆的周长以及面积计算,关键能够理解题目灵活运用公式解答。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
人教版六年级数学上册第五单元圆(知识点梳理+能力百分练)一
知识点梳理
1、圆的定义:圆是由曲线围成的一种平面图形。
2、圆心:将一张圆形纸片对折两次,折痕相交于圆中心的一点,这一点叫做圆心,一般用字母О表示,它到圆上任意一点的距离都相等;
半径:连接圆心到圆上任意一点的线段叫做半径,一般用字母r表示,把圆规两脚分开,两脚之间的距离就是圆的半径;
直径:通过圆心并且两端都在圆上的线段叫做直径,一般用字母d表示,直径是一个圆内最长的线段。
圆心确定圆的位置,半径确定圆的大小。在同圆或等圆内,有无数条半径,有无数条直径。所有的半径都相等,所有的直径都相等。直径的长度是半径的2倍。
3、圆规画圆的步骤:(1)把圆规的两只脚分开,定好两只脚之间的距离;(2)把带针尖的脚固定在一个点上;(3)把装铅笔的脚绕着这个点旋转1圈,就画出了一个圆。
4、圆的周长:围成圆的曲线的长度叫做圆的周长。用字母C表示。任意一个圆的周长与它的直径的比值都是一个固定的数﹐我们把它叫做圆周率,用字母r表示。圆的周长计算公式C=Πd=2Πr。
5、圆的面积:圆所占平面的大小叫做圆的面积。用字母S表示。圆的面积计算公式:S=Πr2。
6、环形的面积:S环=Π(R2 -r2)
7、圆上任意两点之间的部分叫做弧。
8、扇形:一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。在扇形中,顶点在圆心的角叫做圆心角。
能力百分练
一、选择题(共16分)
1.小安在纸上画了两个大小不同的圆,比较这两个圆,( )是相同的。
A.圆周率 B.周长 C.半径 D.面积
2.小东想在空地上围出一块面积为706.5平方米的圆形土地来种菜他应该用多长的篱笆来围(圆周率取3.14)。( )
A.78.5米 B.87.5米 C.92.4米 D.94.2米
3.约2000年前,中国古代数学著作《周髀算经》中就有“周三径一”的说法,意思是说圆的周长约是它的直径的3倍。如果线段AF表示一个圆的周长,那么这个圆的直径可能是线段( )的长。
A.AB B.AD C.CE D.CF
4.观察下图的正方形、圆形、正六边形,下面的想法错误的是( )。
A.圆周长是正方形周长与正六边形周长和的一半
B.正方形周长是圆直径的4倍
C.圆周长比直径的3倍多,比圆的直径4倍少
5.一个周长为25.12cm的圆,直径减少2cm后,面积减少了( )cm2。
A.9.42 B.21.98 C.37.68 D.87.92
6.如图,有一个直径是6厘米的圆在一个宽是6厘米的长方形方框(厚度不计)内平移。这个圆不能覆盖部分的面积是( )平方厘米。
A.7.74 B.15.48 C.28.26 D.36
7.如图,中间是面积为16平方厘米的正方形,与这个正方形每一条边相连的都是圆心角为90°的扇形。那么涂色部分的面积是( )平方厘米。
A.π×12 B.π×22 C.π×42 D.π×62
8.下面三个正方形的边长都是4厘米,三个正方形中阴影部分的面积相比较,( )。
A.图①最大 B.图②最大 C.图③最大 D.同样大
二、填空题(共16分)
9.大圆的半径等于小圆的直径,大圆与小圆的面积之和是80平方厘米,那么大圆的面积是( )平方厘米。
10.如图,把一个圆平均分成若干份,再拼成一个近似的长方形。这个长方形的长与宽的比是( ); 如果这个长方形的长是9.42厘米,那么这个圆的面积是( )平方厘米。
11.如下图,将圆周12等分,那么A点在O点的( )方向,距离( )千米。
12.求阴影部分面积(长度单位:厘米),阴影部分面积是( )平方厘米。
13.小明用圆规画一个圆,圆规两脚张开的距离是3厘米,画出的圆的周长是( )厘米,面积是( )平方厘米。
14.一个边长是2厘米的正方形和一个圆组合在一起,形成了一个新的组合图形(如右上图),两个图形重合部分的面积是正方形面积的( )%。
15.如图中两个圆的直径分别是8厘米和6厘米,阴影部分的面积是( )平方厘米。
16.下图中,线段AD的长度是70厘米,三个圆的直径之比是4∶1∶2,那么,这三个圆的周长之和是( )厘米。
三、判断题(共8分)
17.圆心角为的扇形,一定比圆心角为的扇形面积大。( )
18.在一个长方形里画一个最大的圆,这个新图形仍然是轴对称图形。( )
19.两个圆半径长度的比是1∶2,则它们的面积比也是1∶2。( )
20.用12.56米长的篱笆靠直墙围一个半圆形的鸡舍,鸡舍的占地面积是25.12平方米。( )
四、计算题(共12分)
21.(6分)求图中圆环(阴影部分)的面积和周长。
22.(6分)计算下面阴影部分的面积。(单位:cm)
五、作图题(共6分)
23.(6分)如图,圆从点A开始,沿着直尺向右滚动一周到达B。在直尺上标出点B的大概位置。
六、解答题(共42分)
24.(6分)兰兰用3米长的绳子测量一棵树干横截面的周长,将绳子在树干上绕了3周还余17.4厘米,这棵树干的横截面的面积是多少平方厘米?
25.(6分)海滨公园中有一种“围树座椅”,形状如下图,这种“围树座椅”椅面的面积是多少平方米?
26.(6分)公园里有一个周长是50.24米的花坛,现在要绕花坛周围铺上一条2米宽的水泥路,这条水泥路的面积是多少平方米?
27.(6分)一个圆形餐桌桌面的直径是2米。
(1)如果一个人需要0.7米宽的位置就餐,这张餐桌大约能坐多少人?
(2)如果在这张餐桌的中央放一个半径是0.6米的圆形转盘,剩下的桌面面积是多少?
28.(6分)一张长方形纸,长是20厘米,宽是12厘米,小红用这张长方形纸,剪去一个最大的圆,剩下的边角料的面积是多少平方厘米?
29.(6分)观察下图,按照要求提出数学问题,并解答。
(1)用两步计算的问题:________________________________________
(2)用四步或四步以上计算的问题:_________________________________
30.(6分)李阿姨靠墙围了一个半圆形的菜园,半径是4米(如图)。
(1)围这个菜园需要多长的篱笆?
(2)如果要扩大这个菜园,把它的直径增加2米,菜园的面积增加了多少平方米?
参考答案
1.A
【分析】圆的周长与直径的比是个定值,也就是圆周率,圆的半径大小决定了圆的大小,也决定了圆面积的大小。
【详解】A.圆的周长与直径的比是个定值,也就是圆周率,所以A正确;
B.圆的大小不一样,所以周长不一样,所以B错误;
C.圆的大小不一样,所以半径不一样,所以C错误;
D.圆的大小不一样,所以面积不一样,所以D错误。
故答案为:A
【点睛】考查圆的特点,重点对圆的半径、面积、周长以及圆周率有深刻的理解和认识。
2.D
【分析】先根据圆的面积公式:S=,代入数据求出这块圆形菜地的半径,再根据圆的周长公式:C=,代入半径的数据,即可求出篱笆的长度。
【详解】r2=706.5÷3.14=225
因为15×15=225,
所以圆的半径为15米。
2×3.14×15=94.2(米)
即他应该用94.2米长篱笆来围。
故答案为:D
【点睛】此题的解题关键是灵活运用圆的周长和圆的面积公式求解。
3.C
【分析】由题意可知,圆的周长大约是它直径的3倍,则圆的直径大约占周长的,线段AF表示圆的周长,把AF平均分成3份,圆的直径约占其中的1份,据此解答。
【详解】由图可知,线段AC的长度大约占线段AF长度的,线段AB的长度小于线段AC的长度,线段AD和线段CF的长度大于线段AC的长度,线段CE和线段AC的长度基本相同,所以这个圆的直径可能是线段CE的长。
故答案为:C
【点睛】本题主要考查圆的周长与直径的关系,明确圆的直径大约占它周长的是解答题目的关键。
4.A
【分析】A.圆的直径=正方形边长,圆的半径=正六边形边长,圆的周长=πd,正方形周长=边长×4,正六边形周长=边长×6,据此直接计算即可;
B.圆的直径=正方形边长,正方形周长=边长×4,据此分析;
C.圆的周长=πd,据此分析。
【详解】假设正方形边长是4。
A.圆的周长=3.14×4=12.56
(4×4+4÷2×6)÷2
=(16+12)÷2
=28÷2
=14
圆的周长是12.56,正方形周长与正六边形周长和的一半是14,选项说法错误。
B.正方形周长=边长×4=圆的直径×4,选项说法正确。
C.圆的周长=πd,π一般取值3.14,圆周长比直径的3倍多,比圆的直径4倍少,说法正确。
故答案为:A
【点睛】关键是理解圆、正方形、正六边形之间的关系,掌握并灵活运用正方形和圆的周长公式。
5.B
【分析】先根据“”求出原来圆的直径,再求出现在圆的直径,最后根据“”表示出原来和现在圆的面积,并求出它们的差,据此解答。
【详解】25.12÷3.14=8(cm)
8-2=6(cm)
3.14×(8÷2)2-3.14×(6÷2)2
=3.14×16-3.14×9
=3.14×(16-9)
=3.14×7
=21.98(cm2)
所以,面积减少了21.98cm2。
故答案为:B
【点睛】熟练掌握圆的周长和面积的计算公式是解答题目的关键。
6.A
【分析】如图所示,这个圆不能覆盖的面积是1、2、3、4四部分的面积,把3和4向左平移至3’和4’的位置,这个圆不能覆盖部分的面积=正方形的面积-圆的面积,据此解答。
【详解】6×6-3.14×(6÷2)2
=6×6-3.14×9
=36-28.26
=7.74(平方厘米)
所以,这个圆不能覆盖部分的面积是7.74平方厘米。
故答案为:A
【点睛】准确找出这个圆不能覆盖部分的面积,并把该面积转化为正方形的面积和圆的面积的差是解答题目的关键。
7.C
【分析】根据题意可知,4个扇形可以组成一个圆,圆的半径是正方形的边长,已知正方形的面积是16平方厘米,根据圆面积公式:S=πr2,正方形的面积=边长×边长,可推出半径是4厘米,所以用π×42即可求出4个扇形的面积,阴影部分的面积占4个扇形面积的;用π×42即可求出阴影部分的面积。据此解答。
【详解】16=4×4
扇形的半径是4厘米,
π×42
=π×16
=12π(平方厘米)
涂色部分的面积是12π平方厘米,列式为π×42。
故答案为:C
【点睛】本题主要考查了圆面积公式的灵活应用以及分数乘法的应用,要熟练掌握公式。
8.D
【分析】利用圆的面积公式:S=r2,分别计算各阴影部分的面积,比较即可得出结论。
【详解】图①:3.14×42÷4
=3.14×4×(4÷4)
=3.14×4
=12.56(平方厘米)
图②:3.14×(4÷2)2
=3.14×4
=12.56(平方厘米)
图③:3.14×(4÷2÷2)2×4
=3.14×4
=12.56(平方厘米)
所以三个图形的阴影部分面积相等。
故答案为:D
【点睛】本题主要考查阴影部分的面积,关键利用圆的面积公式计算。
9.64
【分析】根据题意可知,设小圆的半径是x厘米,则大圆的半径是2x厘米,根据圆面积公式,π×2x×2x+π×x2=80,然后求出πx2的值,进而乘4即可求出大圆的面积。
【详解】解:设小圆的半径是x厘米,则大圆的半径是2x厘米。
π×2x×2x+π×x2=80
4πx2+πx2=80
5πx2=80
πx2=80÷5
πx2=16
4πx2
=16×4
=64(平方厘米)
大圆的面积是64平方厘米。
【点睛】本题主要考查了圆面积公式的灵活应用,明确大圆半径和小圆半径之间的关系是解答本题的关键。
10. π∶1 28.26
【分析】由圆的面积推导过程可知:将圆拼成近似的长方形后,长方形的长就等于圆的周长的一半,宽就等于圆的半径,根据圆周长公式:C=2πr,可知圆的周长的一半表示为πr,据此写出这个长方形的长与宽的比,再化简即可;如果这个长方形的长是9.42厘米,则圆的周长是(9.42×2)厘米,根据圆周长公式:C=2πr,用周长÷2÷3.14即可求出圆的半径;最后根据圆面积公式:S=πr2,代入数据解答即可。
【详解】这个长方形的长与宽的比:
πr∶r
=(πr÷r)∶(r÷r)
=π∶1
半径:9.42×2÷2÷3.14=3(厘米)
3.14×32
=3.14×9
=28.26(平方厘米)
把一个圆平均分成若干份,再拼成一个近似的长方形。这个长方形的长与宽的比是π∶1; 如果这个长方形的长是9.42厘米,那么这个圆的面积是28.26平方厘米。
【点睛】本题主要考查了圆周长公式、圆面积公式的灵活应用以及比的化简,解答此题的主要依据是圆的面积推导过程。
11. 东偏北60° 40
【分析】如下图,连接OA,周角是360°,将圆周12等分,所以∠BOA=360°÷12×2=。即A点在O点的东偏北(或北偏东)方向。1个单位长度是10千米,OB是4个单位长度,因为OA、OB都是圆的半径,所以OA=OB,即OA也是4个单位长度。
【详解】如上图,
∠BOA=360°÷12×2=60°,10×4=40(千米)。所以A点在O点的东偏北60°(或北偏东30°)方向,距离是40千米。
【点睛】此题考查了周角的度数、圆心角的度数的求法、根据方向和距离确定物体的位置。
12.37.68
【分析】根据圆环的面积公式:S=π(R2-r2),求出阴影部分的面积即可。
【详解】3.14×(42-22)
=3.14×(16-4)
=3.14×12
=37.68(平方厘米)
阴影部分面积是37.68平方厘米。
【点睛】本题考查的是圆环的面积公式的应用,明确大圆和小圆的半径是解题的关键。
13. 18.84 28.26
【分析】圆规两脚张开的距离是圆的半径,即=3厘米。圆的周长,圆的面积,把半径3厘米分别代入圆的周长公式、面积公式计算即可。
【详解】2×3.14×3
=2×3×3.14
=6×3.14
=18.84(厘米)
3.14×32
=3.14×9
=28.26(平方厘米)
所以画出的圆的周长是18.84厘米,面积是28.26平方厘米。
【点睛】在计算圆的面积时,不要把当成计算,应是。
14.78.5
【分析】已知正方形的边长是2厘米,根据正方形的面积公式S=a2,求出正方形的面积;
从图中可知,圆的半径等于正方形的边长;根据圆的面积公式S=πr2,求出圆的面积,再乘,即是两个图形重合部分的面积;
然后用两个图形重合部分的面积除以正方形面积,求出重合部分的面积是正方形面积的百分之几。
【详解】正方形的面积:
2×2=4(平方厘米)
两个图形重合部分的面积:
3.14×22×
=3.14×4×
=3.14(平方厘米)
3.14÷4×100%
=0.785×100%
=78.5%
两个图形重合部分的面积是正方形面积的78.5%。
【点睛】本题考查正方形的面积、圆的面积公式的运用,明确根据求一个数是另一个数的百分之几,用除法计算。
15.21.98
【分析】观察图形可知,阴影部分的面积=大圆的面积-小圆的面积,根据圆的面积公式S=πr2,代入数据计算即可求解。
【详解】3.14×(8÷2)2-3.14×(6÷2)2
=3.14×16-3.14×9
=50.24-28.26
=21.98(平方厘米)
阴影部分的面积是21.98平方厘米。
【点睛】本题考查圆的面积公式的运用,关键是观察图形,分析出阴影部分的面积是由哪些图形面积相减得到,再根据图形的面积公式列式计算。
16.219.8
【分析】把根据圆周长公式:C=πd,可知三个圆的周长和=3.14×AB+3.14×BC+3.14×CD,根据乘法分配律,可知三个圆的周长和=3.14×(AB+BC+CD)=3.14×AD,据此用3.14×70即可求出三个圆的周长和。
【详解】3.14×70=219.8(厘米)
这三个圆的周长之和是219.8厘米。
【点睛】本题主要考查了圆周长公式的灵活应用以及比的应用,这里可以应用圆的周长公式计算,比计算出每个直径的长度更简便。
17.×
【分析】计算扇形面积需要知道半径的大小和圆心角,只知道圆心角而不知道半径,则无法计算扇形的面积,也就无法比较大小。
【详解】计算扇形面积需要知道圆心角和半径,不知道半径的大小,就无法计算面积,也就不能比较面积大小了;所以原题说法错误。
故答案为:×
【点睛】此题主要考查扇形面积的计算方法,注意扇形的面积的大小是由圆心角的度数和半径的大小决定的。
18.√
【分析】如果一个平面图形沿着一条直线对折后,直线两侧的部分能够完全重合,那么这个图形就叫作轴对称图形,这条直线就叫作这个图形的对称轴。长方形是轴对称图形,有2条对称轴;圆是轴对称图形,有无数条对称轴。如下图,
、。
先根据题意画出图形,再根据轴对称的意义判断即可。
【详解】在一个长方形里画一个最大的圆,圆的直径等于长方形的宽。如下图,得到的新图形仍然是轴对称图形,有1条或2条对称轴。原题说法正确。
、
故答案为:√
【点睛】判断组合图形是不是轴对称图形时,要把这些图形看作一个整体,尝试从不同的位置对折。
19.×
【分析】圆的面积,所以圆的面积之比等于圆半径的平方之比,据此判断即可。
【详解】两个圆半径长度的比是1∶2,则它们的面积比是,本题说法错误;
故答案为:×。
【点睛】本题考查比、圆的面积,解答本题的关键是掌握比的意义。
20.√
【分析】由题意可知,篱笆的长度就是整圆周长的一半,据此求出圆的半径,再根据圆的面积公式:S=πr2,据此求出整圆的面积,再除以2就是鸡舍的占地面积。
【详解】12.56÷3.14=4(米)
3.14×42÷2
=3.14×16÷2
=50.24÷2
=25.12(平方米)
则鸡舍的占地面积是25.12平方米。原题干说法正确。
故答案为:√
【点睛】本题考查圆的周长和面积,熟记公式是解题的关键。
21.200.96平方厘米;100.48厘米
【分析】由图可知,大圆的半径为10厘米,小圆的半径为6厘米,利用“”求出圆环的面积;圆环的周长=大圆的周长+小圆的周长,利用“”求出圆环的周长,据此解答。
【详解】面积:3.14×(102-62)
=3.14×(100-36)
=3.14×64
=200.96(平方厘米)
周长:2×3.14×10+2×3.14×6
=2×3.14×(10+6)
=2×3.14×16
=6.28×16
=100.48(厘米)
所以,圆环的面积是200.96平方厘米,圆环的周长是100.48厘米。
22.86cm2
【分析】阴影部分的面积=正方形面积-圆的面积,正方形面积=边长×边长,圆的面积=πr2,据此列式计算。
【详解】20×20-3.14×(20÷2)2
=400-3.14×102
=400-3.14×100
=400-314
=86(cm2)
23.见详解
【分析】圆的周长=πd,点A在刻度5,点A所在刻度+圆的周长=点B所在刻度,据此分析。
【详解】3.14×2=6.28
5+6.28=11.28
【点睛】关键是掌握并灵活运用圆的周长公式。
24.706.5平方厘米
【分析】先用绳子的长减去17.4厘米,再除以3求出树干横截面的周长;由圆的周长可推导出,据此根据圆的周长求出圆的半径;最后利用圆的面积求出这棵树干的横截面的面积。
【详解】3米=300厘米
(300-17.4)÷3
=282.6÷3
=94.2(厘米)
94.2÷3.14÷2
=30÷2
=15(厘米)
3.14×152
=3.14×225
=706.5(平方厘米)
答:这棵树干的横截面的面积是706.5平方厘米。
【点睛】此题考查了圆的周长、圆的面积计算公式。在计算圆的面积时,不要把当成计算,应是。
25.9.42平方米
【分析】观察图形可知,这种“围树座椅”椅面的面积就是圆环的面积,根据圆环的面积公式:S=π(R2-r2),据此计算即可。
【详解】3.14×[(4÷2)2-(2÷2)2]
=3.14×[22-12]
=3.14×[4-1]
=3.14×3
=9.42(平方米)
答:这种“围树座椅”椅面的面积是9.42平方米。
【点睛】本题考查圆环的面积,熟记公式是解题的关键。
26.113.04平方米
【分析】水泥路的形状是个圆环,根据圆的半径=周长÷π÷2,先求出花坛半径,即小圆半径,小圆半径+路宽=大圆半径,确定大圆和小圆半径,根据圆环面积=π(R2-r2),列式解答即可。
【详解】50.24÷3.14÷2=8(米)
8+2=10(米)
3.14×(102-82)
=3.14×(100-64)
=3.14×36
=113.04(平方米)
答:这条水泥路的面积是113.04平方米。
【点睛】关键是掌握并灵活运用圆的周长和圆环面积公式。
27.(1)9人;(2)2.0096平方米
【分析】(1)根据圆的周长=πd,求出餐桌周长,餐桌周长÷一个人需要的长度=坐的人数,结果用四舍五入法保留整数即可。
(2)剩下的面积是个圆环,确定大圆和小圆的半径,根据圆环面积=π(R2-r2),列式解答即可。
【详解】(1)
(人
答:这张餐桌大约能坐9人。
(2)(米)
(平方米)
答:剩下的桌面面积是2.0096平方米。
【点睛】关键是掌握并灵活运用圆的周长和圆环面积公式。
28.126.96平方厘米
【分析】根据题意,可得最大的圆的直径是长方形的宽;然后用12除以2,求出圆的半径,进而求出圆的面积;最后用长方形的面积减去圆的面积,求出剩下的边角料的面积是多少平方厘米即可。
【详解】根据题意,可得最大的圆的直径是长方形的宽
即圆的直径是12厘米
20×12-3.14×(12÷2)2
=240-3.14×36
=240-113.04
=126.96(平方厘米)
答:剩下的边角料的面积是126.96平方厘米。
【点睛】解答此题的关键是熟练掌握长方形和圆的面积的求法。
29.(1)正方形的周长是多少厘米?16厘米;(2)阴影部分的面积是多少平方厘米?3.44平方厘米
【分析】问题合理即可,没有固定答案。例如:
(1)正方形的周长是多少厘米?正方形的边长相当于圆的直径,则用2×2×4即可求正方形周长。
(2)阴影部分的面积是多少平方厘米?根据正方形面积公式和圆面积公式求出正方形的面积和圆面积,然后求出它们的差即可。
【详解】(1)正方形的周长是多少厘米?
直径:2×2=4(厘米)
周长:4×4=16(厘米)
答:正方形的周长是16厘米。(答案不唯一)
(2)阴影部分的面积是多少平方厘米?
4×4 3.14×22
=4×4 3.14×4
=16 12.56
=3.44(平方厘米)
答:阴影部分的面积是3.44平方厘米。(答案不唯一)
【点睛】本题主要考查组合图形的面积,关键利用规则图形的面积公式计算。
30.(1)12.56米
(2)14.13平方米
【分析】(1)根据题意,篱笆是圆周长的一半,用公式:圆周长的一半=πr,将数据代入计算即可;
(2)直径增加2米,也就是半径增加1米,用公式:半圆的面积=πr2÷2,计算出原来菜园的面积与新的面积相减即可得出新增加了多少平方米。
【详解】(1)4×3.14=12.56(米)
答:围这个菜园需要12.56米的篱笆。
(2)2÷2=1(米)
4+1=5(米)
5×5×3.14÷2-4×4×3.14÷2
=25×3.14÷2-16×3.14÷2
=78.5÷2-50.24÷2
=39.25-25.12
=14.13(平方米)
答:菜园的面积增加了14.13平方米。
【点睛】此题考查了圆的周长以及面积计算,关键能够理解题目灵活运用公式解答。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
