第1章 直角三角形的边角关系单元测试题(含解析)
文档属性
| 名称 | 第1章 直角三角形的边角关系单元测试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 832.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-25 18:12:16 | ||
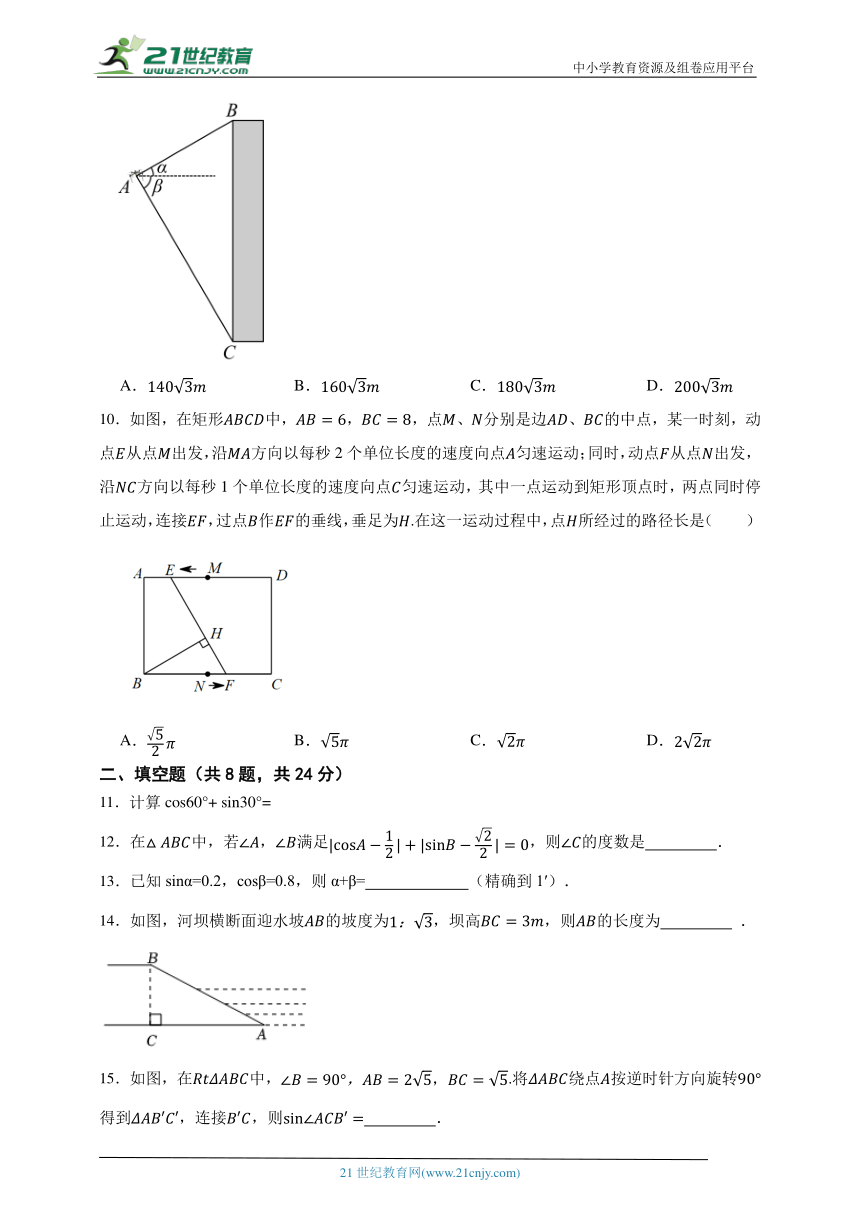
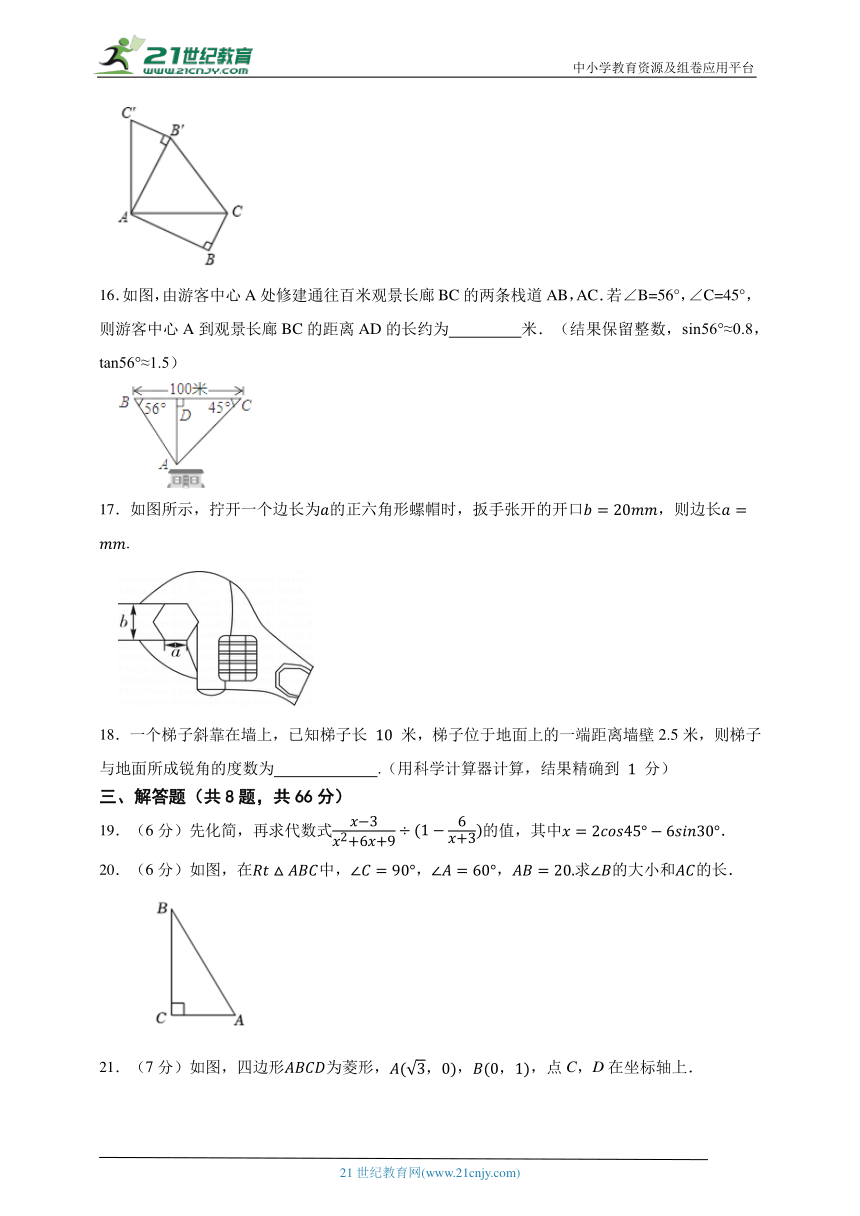
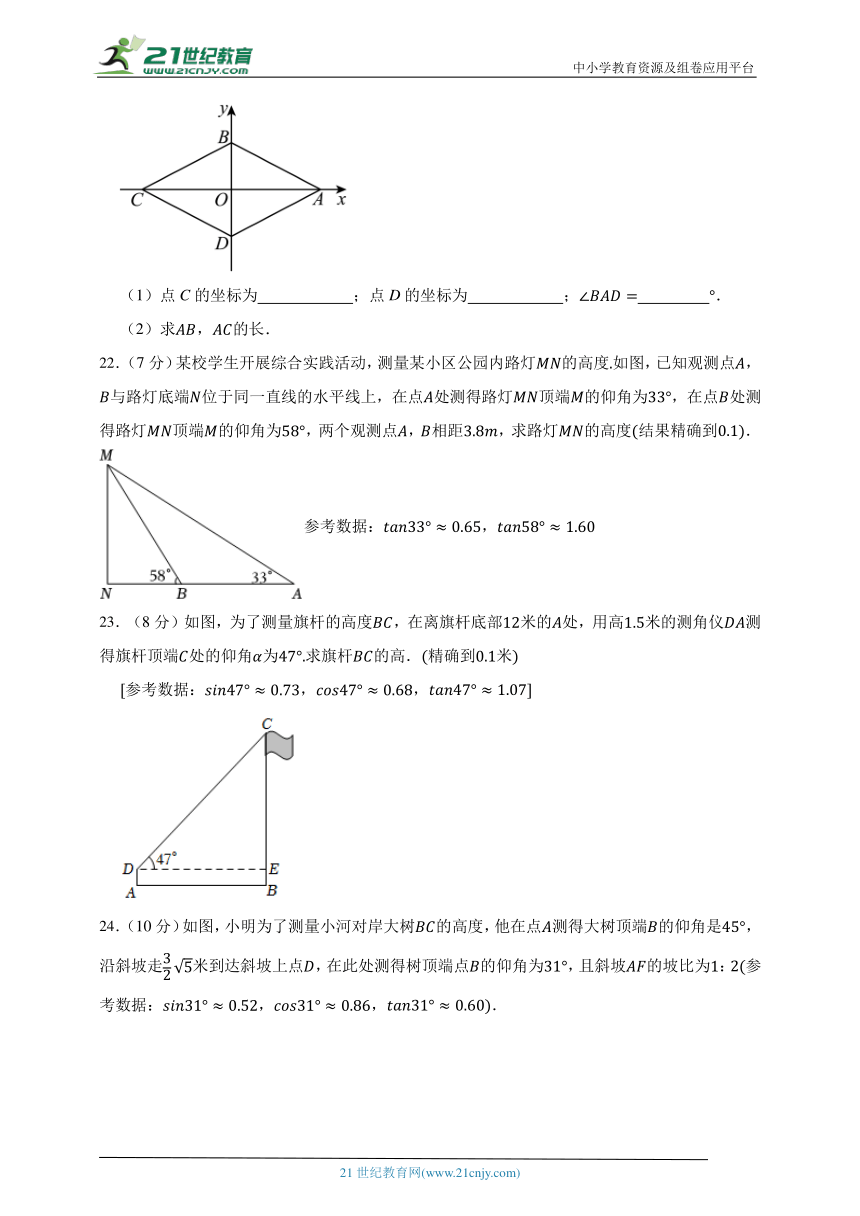
图片预览


文档简介
中小学教育资源及组卷应用平台
2023-2024学年北师大版九年级数学下册 第1章 直角三角形的边角关系 单元测试题
一、选择题(共10题,共30分)
1.在中,若角,满足,则的大小是( )
A. B. C. D.
2.如图,在高为,坡角为的楼梯上铺地毯,地毯的长度至少应为( )
A. B. C. D.
3.在Rt△ABC中,∠C=90°,若sinA=,则∠A的度数是( )
A.60° B.45° C.30° D.无法确定
4.若用我们数学课本上采用的科学计算器计算,按键顺序正确的是( )
A. B.
C. D.
5.如图所示,已知在平面直角坐标系中,点A,B的坐标分别为,点是轴正半轴上的一点,且满足,现有以下4个结论:①的外接圆的圆心在OC上;②∠ABC=60°;③△ABC的外接圆的半径等于;④.其中正确的是( ).
A.①② B.②③ C.③④ D.①④
6.西周时期,丞相周公且设置过一种通过测定日影长度来确定时间的仪器,称为圭表如图是一个根据北京的地理位置设计的圭表,其中,立柱高为已知,冬至时北京的正午日光入射角约为,则立柱根部与圭表的冬至线的距离即的长约为( )
A. B. C. D.
7.如图,一款可调节的笔记本电脑支架放置在水平桌面上,调节杆的最大仰角为.当时,则点到桌面的最大高度是( )
A. B. C. D.
8.如图,在综合实践活动中,小明在学校门口的点处测得树的顶端仰角为,同时测得米,则树的高(单位:米)为( )
A. B. C. D.
9.如图,从航拍无人机看一栋楼顶部的仰角为,看这栋楼底部的俯角为,无人机与楼的水平距离为,则这栋楼的高度为( )
A. B. C. D.
10.如图,在矩形中,,,点、分别是边、的中点,某一时刻,动点从点出发,沿方向以每秒2个单位长度的速度向点匀速运动;同时,动点从点出发,沿方向以每秒1个单位长度的速度向点匀速运动,其中一点运动到矩形顶点时,两点同时停止运动,连接,过点作的垂线,垂足为.在这一运动过程中,点所经过的路径长是( )
A. B. C. D.
二、填空题(共8题,共24分)
11.计算cos60°+ sin30°=
12.在中,若,满足,则的度数是 .
13.已知sinα=0.2,cosβ=0.8,则α+β= (精确到1′).
14.如图,河坝横断面迎水坡的坡度为,坝高,则的长度为 .
15.如图,在中,.将绕点按逆时针方向旋转得到,连接,则 .
16.如图,由游客中心A处修建通往百米观景长廊BC的两条栈道AB,AC.若∠B=56°,∠C=45°,则游客中心A到观景长廊BC的距离AD的长约为 米.(结果保留整数,sin56°≈0.8,tan56°≈1.5)
17.如图所示,拧开一个边长为的正六角形螺帽时,扳手张开的开口,则边长 .
18.一个梯子斜靠在墙上,已知梯子长 米,梯子位于地面上的一端距离墙壁2.5米,则梯子与地面所成锐角的度数为 .(用科学计算器计算,结果精确到 分)
三、解答题(共8题,共66分)
19.(6分)先化简,再求代数式的值,其中.
20.(6分)如图,在中,,,求的大小和的长.
21.(7分)如图,四边形为菱形,,,点C,D在坐标轴上.
(1)点C的坐标为 ;点D的坐标为 ; .
(2)求,的长.
22.(7分)某校学生开展综合实践活动,测量某小区公园内路灯的高度如图,已知观测点,与路灯底端位于同一直线的水平线上,在点处测得路灯顶端的仰角为,在点处测得路灯顶端的仰角为,两个观测点,相距,求路灯的高度结果精确到.
参考数据:,
23.(8分)如图,为了测量旗杆的高度,在离旗杆底部米的处,用高米的测角仪测得旗杆顶端处的仰角为求旗杆的高.精确到米
参考数据:,,
24.(10分)如图,小明为了测量小河对岸大树的高度,他在点测得大树顶端的仰角是,沿斜坡走米到达斜坡上点,在此处测得树顶端点的仰角为,且斜坡的坡比为:参考数据:,,.
(1)求小明从点走到点的过程中,他上升的高度;
(2)大树的高度约为多少米?
25.(10分)我校中学数学兴趣小组借助无人机测量一条河流的宽,如图所示,一架水平飞行的无人机在处测得正前方河流的左岸处的俯角为,无人机的正东方向继续飞行米至处,测得正前方河流右岸处的俯角为,线段的长为无人机距地面的垂直高度,点、、在同一条直线上,其中,米
(1)求无人机的飞行高度结果保留根号
(2)求河流的宽度结果精确到米,参考数据:,
26.(12分)爬山能强身健体,亲近自然,陶冶情操,王老师周末到公园爬山,山的形状如图,爬山路线示意图如图,王老师从山脚出发,沿走米到点,再沿到山顶点,已知山高为米,,,交的延长线于点,,图中所有点均在同一平面内
(1)求的长;
(2)求王老师从山脚点到达山顶点共走了多少米?结果精确到米参考数据:,,
答案解析部分
1.【答案】D
【知识点】三角形内角和定理;锐角三角函数的定义;实数的绝对值
【解析】【解答】解:由题意可得:
,解得:
A,B,C是三角形的内角
∴∠A=30°,∠B=45°
则∠C=180°-∠A-∠B=105°
故答案为:D
【分析】根据绝对值与二次根式的性质可求出,再根据三角形中内角的三角函数值的性质可得∠A=30°,∠B=45°,再根据三角形内角和定理即可求出答案.
2.【答案】D
【知识点】锐角三角函数的定义
【解析】【解答】解:由题意可得:地毯的长度为AB+AC长
∵BC=2,∠BAC=30°
则
∴
故答案为:D
【分析】在直角三角形中,根据锐角三角函数定义可求出AB长,再根据地毯的长度为AB+AC的长即可求出答案.
3.【答案】C
【知识点】特殊角的三角函数值
【解析】【解答】解:∵Rt△ABC中,∠C=90°,
∵sin30°= ,
∴∠A=30°.
故答案为:C.
【分析】由特殊角的三角函数值计算即可解答.
4.【答案】D
【知识点】计算器—三角函数
【解析】【解答】解:科学计算器计算,按键顺序是,
故答案为:D.
【分析】 根据科学计算器的使用方法知:按键顺序是.
5.【答案】C
【知识点】垂径定理;圆周角定理;三角形的外接圆与外心;解直角三角形;等腰直角三角形
【解析】【解答】解:如图,作出△ABC的外接圆,以AB为斜边在x轴上方作等腰直角三角形ABE,过点E作ED⊥x轴于点D,连接EC,过点E作EF⊥y轴于点F,
∵△ABC的外接圆的圆心一定在弦AB的垂直平分线上,
∴圆心肯定不在OC上,故①错误;
∵∠ACB=45°,
∴由圆周角定理得弧AB所对的圆心角一定为90°,
∵∠AEB=90°,
∴点E必为圆心,即AE、BE为半径,
∵A(4,0),B(-6,0),
∴AB=10,
在Rt△ABE中,AE2+BE2=AB2,∴AE=,故③正确;
∵AB=10,DE⊥AB,
∴AD=BD=5,
又∵OB=6,
∴OD=1,
∵∠EDO=∠DOF=∠OFE=90°,
∴四边形EDOF是矩形,
∴EF=OD=1,ED=OF=5,
在Rt△CEF中,由勾股定理得CF=7,
∴OF=12,故④正确;
∵,
∴∠ABC≠60°,故②错误.
故答案为:C.
【分析】作出△ABC的外接圆,以AB为斜边在x轴上方作等腰直角三角形ABE,过点E作ED⊥x轴于点D,连接EC,过点E作EF⊥y轴于点F,由垂径定理可得圆心一定在弦的垂直平分线上可判断①;再根据圆周角定理证出点E为△ABNC外接圆的圆心,利用勾股定理求出半径可判断③;判断出四边形EDOF是矩形,得EF=OD=1,ED=OF=5,再在Rt△ECF中利用勾股定理算出CF,可求出OC的长及∠ABC的正切值,从而即可判断②④.
6.【答案】D
【知识点】解直角三角形的应用
【解析】【解答】根据题意可得:
立柱根部与圭表的冬至线的距离为:,
故答案为:D.
【分析】利用正切的定义可得,再求出即可.
7.【答案】D
【知识点】解直角三角形的应用
【解析】【解答】解:如图,过点A作AF⊥BE于点F,过点B作BG⊥CD于点G;
∵AF⊥BE于点F,BG⊥CD于点G,
∴∠AFB=∠BGC=90°,
在Rt△ABF中,,∴,
在Rt△BCG中,,
∴,
∴点A到桌面的最大高度为AF+BG= .
故答案为:D.
【分析】过点A作AF⊥BE于点F,过点B作BG⊥CD于点G;在Rt△ABF中,利用∠ABF的正弦函数可表示出AF,在Rt△BCG中,利用∠BCG的正弦函数可表示出BG,最后根据点A到桌面的最大高度为:AF+BG,可算出答案.
8.【答案】B
【知识点】解直角三角形的应用﹣仰角俯角问题
【解析】【解答】解:在Rt△ABC中,∵∠ABC=90°,
∴,
又∵BC=20米,∠C=37°,
∴AB=BC×tan37°=20tan37°.
故答案为:B.
【分析】在Rt△ABC中,由∠C的正切函数可直接求出AB的长.
9.【答案】B
【知识点】解直角三角形的应用﹣仰角俯角问题
【解析】【解答】解:过点A作AD⊥BC于点D,
由题意可知,∠BAD=30°,∠CAD=60°,
在Rt△ABD中,
,
在Rt△ACD中
,
∴.
故答案为:B
【分析】过点A作AD⊥BC于点D,在Rt△ABD和Rt△ACD中,利用解直角三角形分别求出BD,CD的长,然后根据BC=CD+BD,代入计算求出BC的长.
10.【答案】A
【知识点】勾股定理;矩形的判定与性质;圆周角定理;弧长的计算;相似三角形的判定与性质
【解析】【解答】解:如图1中,连接交于点,连接.
四边形是矩形,,,
四边形是矩形,
,
,
,
,
,,
,
,
,
,
点在为直径的上运动,
当点与重合时,如图2中,连接,.点的运动轨迹是.
此时,,
,
,,
平分,
,
,
点的运动轨迹的长.
故答案为:A.
【分析】连接交于点,连接.证明,利用相似三角形的性质可得PN=2,PM=4,利用勾股定理求出BP=,由垂直的定义可得,可得点在为直径的上运动,当点与重合时,如图2中,连接,.点的运动轨迹是,利用弧长公式计算即可.
11.【答案】1
【知识点】特殊角的三角函数值
12.【答案】75°
【知识点】三角形内角和定理;特殊角的三角函数值;非负数之和为0
【解析】【解答】解:∵,
∴,,
∴,,
∴∠A=60°,∠B=45°,
∴∠C=180°-∠A-∠B=75°,
故答案为:75°.
【分析】根据题意先求出,,再利用特殊角的锐角三角函数值求出∠A=60°,∠B=45°,最后利用三角形的内角和计算求解即可。
13.【答案】48°24′
【知识点】计算器—三角函数
【解析】【解答】解:48°24′.
【分析】根据已知一个角的三角函数值求这个角的算法:先按MODE,选择模式.再键入数字,最后按2ndF和sin或cos,得到这三个角的度数.
14.【答案】6m
【知识点】解直角三角形的应用﹣坡度坡角问题
【解析】【解答】∵河坝横断面迎水坡的坡度为,
∴,
∵,
∴,
在Rt△ABC中,由勾股定理可得:,
故答案为:6.
【分析】先利用坡度比可得,再求出AC的长,最后利用勾股定理求出AB的长即可.
15.【答案】
【知识点】解直角三角形的应用;旋转的性质
【解析】【解答】解:过点B'作B'D⊥AC于点D,如图,
∵将绕点按逆时针方向旋转得到,
∴∠BAB'=90°,
∵∠ABC=90°,
∴BC∥AB',
∴∠B'AD=∠ACB,
在Rt△ABC中,,
,
,
在Rt△AB'D中,
,,
设AD=m,B'D=2m,
∴,
∴,
解得:m=2,
∴AD=2,B'D=4,
∴CD=AC-AD=5-2=3,
在Rt△B'CD中,
B'D=4,CD=3,
∴,
∴.
故答案为: .
【分析】过点B'作B'D⊥AC于点D,由旋转得∠BAB'=90°,因此BC∥AB',得∠B'AD=∠ACB,在Rt△ABC中得AC长和,在Rt△AB'D中,得AD、B'D长,在Rt△B'CD中,求得CD、B'C的长,即可求解.
16.【答案】60
【知识点】解直角三角形的应用
【解析】【解答】解:∵∠B=56°,∠C=45°,∠ADB=∠ADC=90°,BC=BD+CD=100米,
∴BD= ,CD= ,
∴ + =100,
解得AD≈60.
故答案为:60.
【分析】根据已知和三角函数的定义,得到BC=BD+CD的值,求出AD的值.
17.【答案】
【知识点】解直角三角形;正多边形的性质
【解析】【解答】解:如图,设正六边形ABCDEF的中心为O,连接OC、OD,过点O作OG⊥CD于点G,
∵∠COD=,OC=OD,
∴△COD是等边三角形,
又∵OG⊥CD,
∴∠COG=∠COD=30°,CD=2CG=a,OG=b=10mm,
∴CG=tan∠COG×OG=tan30°×10=mm,
∴a=CD=2CG=mm.
故答案为:.
【分析】设该六边形的中心为O,连接OC、OD,过点O作OG⊥CD于点G,由正多边形的中心角求法可得∠COD=60°,由有一个角为60°的等腰三角形是等边三角形得△COD是等边三角形,由等腰三角形的三线合一得∠COG=∠COD=30°,CD=2CG=a,根据正多边形的对称性得OG=b=10mm,从而由∠COG的正切函数可求出CG,此题得解.
18.【答案】75°31′
【知识点】锐角三角函数的定义;计算器—三角函数;近似数及有效数字
【解析】【解答】解:设一个梯子斜靠在墙上,梯子与地面所成锐角为 ,
∵梯子长10米,梯子位于地面上的一端距离墙壁2.5米,
∴ ,
解得: .
故答案为:75°31′.
【分析】设梯子与地面所成锐角为α,根据三角函数的概念可得cosα==,然后利用计算器进行计算即可.
19.【答案】解:原式
,
当时,原式.
【知识点】分式的化简求值;特殊角的三角函数值
【解析】【分析】将括号内通分并利用同分母分式减法法则计算,再将除法转化为乘法,进行约分即可化简,最后利用特殊角三角函数值求出x值,然后代入计算即可.
20.【答案】解:
;
,
;
答:,.
【知识点】三角形内角和定理;含30°角的直角三角形;锐角三角函数的定义
【解析】【分析】
根据三角形内角和定理求出∠B,再运用三角函数求出AC,也可根据含有30度角的直角三角形的性质求出AC。
21.【答案】(1);;60
(2)解:由(1)得:,
∵,
∴.
【知识点】菱形的性质;解直角三角形
【解析】【解答】解:(1)∵,,
∴OA=,OB=1,
∵四边形为菱形,
∴OC=OA=,OB=OD=1,∠BAD=2∠BAO,∠AOB=90°,
∴点C的坐标为(-,0),点D的坐标为(0,-1),
∵tan∠BAO=,
∴∠BAO=30°,
∴∠BAD=2∠BAO=60°,
故答案为:,,60.
【分析】(1)利用菱形的性质求出OC=OA=,OB=OD=1,∠BAD=2∠BAO,∠AOB=90°,可得点C、D的坐标,再利用解直角三角形的性质求出∠BAO=30°,可得∠BAD=2∠BAO=60°;
(2)利用勾股定理求出AB的长,再结合点A、C的坐标求出AC的长即可.
22.【答案】解:由题意得:,
设米,
米,
米,
在中,,
米,
在中,,
米,
,
解得:,
米,
【知识点】解直角三角形的应用﹣仰角俯角问题
【解析】【分析】设米,先求出,再利用解直角三角形的方法可得,,可得,再求出x的值即可.
23.【答案】解:过点作交于,
则米,
在中,有米,
米
故BC米,
答:旗杆的高度约为米.
【知识点】解直角三角形的应用
【解析】【分析】如图,过点D作DE⊥BC于E,在Rt△DEC中,DE=12,tan47°≈1.07,则可求出CE=12.8,再根据BE=1.5,BC=CE+BE即可求解。
24.【答案】(1)解:作于,如图.
在中,,
,
,
,
.
故他上升的高度为米;
(2)解:如图,延长交于点,设,
由题意得,,
,
,
,
在中,,
,
在中,,
.
,
,
解得.
答:大树的高度约为米.
【知识点】解直角三角形的应用﹣仰角俯角问题
【解析】【分析】(1)在直角三角形中,根据勾股定理即可求出答案.
(2)在直角三角形中,根据锐角三角形函数的定义即可求出答案.
25.【答案】(1)解:由题意得:
,
,
在中,米,
米,
无人机的飞行高度为米;
(2)解:过点作,垂足为,
则米,,
在中,,
米,
米,
米,
米,
河流的宽度约为米.
【知识点】平行线的性质;解直角三角形的应用﹣仰角俯角问题
【解析】【分析】(1)根据直线平行性质,可得,在中,解直角三角形即可求出答案。
(2)过点作,垂足为, 可得米,,在中,解直角三角形即可求出答案。
26.【答案】(1)解:在中,米,,
米,
的长为米;
(2)解:由题意得:米,
米,
米,
在中,,
米,
米,
王老师从山脚点到达山顶点共走了约米.
【知识点】含30°角的直角三角形;解直角三角形的应用﹣坡度坡角问题
【解析】【分析】(1)在中,根据含30度角的直角三角形的性质,即可求解;
(2)由题意得:米,在中,,根据正弦的定义求得BC,即可求解.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023-2024学年北师大版九年级数学下册 第1章 直角三角形的边角关系 单元测试题
一、选择题(共10题,共30分)
1.在中,若角,满足,则的大小是( )
A. B. C. D.
2.如图,在高为,坡角为的楼梯上铺地毯,地毯的长度至少应为( )
A. B. C. D.
3.在Rt△ABC中,∠C=90°,若sinA=,则∠A的度数是( )
A.60° B.45° C.30° D.无法确定
4.若用我们数学课本上采用的科学计算器计算,按键顺序正确的是( )
A. B.
C. D.
5.如图所示,已知在平面直角坐标系中,点A,B的坐标分别为,点是轴正半轴上的一点,且满足,现有以下4个结论:①的外接圆的圆心在OC上;②∠ABC=60°;③△ABC的外接圆的半径等于;④.其中正确的是( ).
A.①② B.②③ C.③④ D.①④
6.西周时期,丞相周公且设置过一种通过测定日影长度来确定时间的仪器,称为圭表如图是一个根据北京的地理位置设计的圭表,其中,立柱高为已知,冬至时北京的正午日光入射角约为,则立柱根部与圭表的冬至线的距离即的长约为( )
A. B. C. D.
7.如图,一款可调节的笔记本电脑支架放置在水平桌面上,调节杆的最大仰角为.当时,则点到桌面的最大高度是( )
A. B. C. D.
8.如图,在综合实践活动中,小明在学校门口的点处测得树的顶端仰角为,同时测得米,则树的高(单位:米)为( )
A. B. C. D.
9.如图,从航拍无人机看一栋楼顶部的仰角为,看这栋楼底部的俯角为,无人机与楼的水平距离为,则这栋楼的高度为( )
A. B. C. D.
10.如图,在矩形中,,,点、分别是边、的中点,某一时刻,动点从点出发,沿方向以每秒2个单位长度的速度向点匀速运动;同时,动点从点出发,沿方向以每秒1个单位长度的速度向点匀速运动,其中一点运动到矩形顶点时,两点同时停止运动,连接,过点作的垂线,垂足为.在这一运动过程中,点所经过的路径长是( )
A. B. C. D.
二、填空题(共8题,共24分)
11.计算cos60°+ sin30°=
12.在中,若,满足,则的度数是 .
13.已知sinα=0.2,cosβ=0.8,则α+β= (精确到1′).
14.如图,河坝横断面迎水坡的坡度为,坝高,则的长度为 .
15.如图,在中,.将绕点按逆时针方向旋转得到,连接,则 .
16.如图,由游客中心A处修建通往百米观景长廊BC的两条栈道AB,AC.若∠B=56°,∠C=45°,则游客中心A到观景长廊BC的距离AD的长约为 米.(结果保留整数,sin56°≈0.8,tan56°≈1.5)
17.如图所示,拧开一个边长为的正六角形螺帽时,扳手张开的开口,则边长 .
18.一个梯子斜靠在墙上,已知梯子长 米,梯子位于地面上的一端距离墙壁2.5米,则梯子与地面所成锐角的度数为 .(用科学计算器计算,结果精确到 分)
三、解答题(共8题,共66分)
19.(6分)先化简,再求代数式的值,其中.
20.(6分)如图,在中,,,求的大小和的长.
21.(7分)如图,四边形为菱形,,,点C,D在坐标轴上.
(1)点C的坐标为 ;点D的坐标为 ; .
(2)求,的长.
22.(7分)某校学生开展综合实践活动,测量某小区公园内路灯的高度如图,已知观测点,与路灯底端位于同一直线的水平线上,在点处测得路灯顶端的仰角为,在点处测得路灯顶端的仰角为,两个观测点,相距,求路灯的高度结果精确到.
参考数据:,
23.(8分)如图,为了测量旗杆的高度,在离旗杆底部米的处,用高米的测角仪测得旗杆顶端处的仰角为求旗杆的高.精确到米
参考数据:,,
24.(10分)如图,小明为了测量小河对岸大树的高度,他在点测得大树顶端的仰角是,沿斜坡走米到达斜坡上点,在此处测得树顶端点的仰角为,且斜坡的坡比为:参考数据:,,.
(1)求小明从点走到点的过程中,他上升的高度;
(2)大树的高度约为多少米?
25.(10分)我校中学数学兴趣小组借助无人机测量一条河流的宽,如图所示,一架水平飞行的无人机在处测得正前方河流的左岸处的俯角为,无人机的正东方向继续飞行米至处,测得正前方河流右岸处的俯角为,线段的长为无人机距地面的垂直高度,点、、在同一条直线上,其中,米
(1)求无人机的飞行高度结果保留根号
(2)求河流的宽度结果精确到米,参考数据:,
26.(12分)爬山能强身健体,亲近自然,陶冶情操,王老师周末到公园爬山,山的形状如图,爬山路线示意图如图,王老师从山脚出发,沿走米到点,再沿到山顶点,已知山高为米,,,交的延长线于点,,图中所有点均在同一平面内
(1)求的长;
(2)求王老师从山脚点到达山顶点共走了多少米?结果精确到米参考数据:,,
答案解析部分
1.【答案】D
【知识点】三角形内角和定理;锐角三角函数的定义;实数的绝对值
【解析】【解答】解:由题意可得:
,解得:
A,B,C是三角形的内角
∴∠A=30°,∠B=45°
则∠C=180°-∠A-∠B=105°
故答案为:D
【分析】根据绝对值与二次根式的性质可求出,再根据三角形中内角的三角函数值的性质可得∠A=30°,∠B=45°,再根据三角形内角和定理即可求出答案.
2.【答案】D
【知识点】锐角三角函数的定义
【解析】【解答】解:由题意可得:地毯的长度为AB+AC长
∵BC=2,∠BAC=30°
则
∴
故答案为:D
【分析】在直角三角形中,根据锐角三角函数定义可求出AB长,再根据地毯的长度为AB+AC的长即可求出答案.
3.【答案】C
【知识点】特殊角的三角函数值
【解析】【解答】解:∵Rt△ABC中,∠C=90°,
∵sin30°= ,
∴∠A=30°.
故答案为:C.
【分析】由特殊角的三角函数值计算即可解答.
4.【答案】D
【知识点】计算器—三角函数
【解析】【解答】解:科学计算器计算,按键顺序是,
故答案为:D.
【分析】 根据科学计算器的使用方法知:按键顺序是.
5.【答案】C
【知识点】垂径定理;圆周角定理;三角形的外接圆与外心;解直角三角形;等腰直角三角形
【解析】【解答】解:如图,作出△ABC的外接圆,以AB为斜边在x轴上方作等腰直角三角形ABE,过点E作ED⊥x轴于点D,连接EC,过点E作EF⊥y轴于点F,
∵△ABC的外接圆的圆心一定在弦AB的垂直平分线上,
∴圆心肯定不在OC上,故①错误;
∵∠ACB=45°,
∴由圆周角定理得弧AB所对的圆心角一定为90°,
∵∠AEB=90°,
∴点E必为圆心,即AE、BE为半径,
∵A(4,0),B(-6,0),
∴AB=10,
在Rt△ABE中,AE2+BE2=AB2,∴AE=,故③正确;
∵AB=10,DE⊥AB,
∴AD=BD=5,
又∵OB=6,
∴OD=1,
∵∠EDO=∠DOF=∠OFE=90°,
∴四边形EDOF是矩形,
∴EF=OD=1,ED=OF=5,
在Rt△CEF中,由勾股定理得CF=7,
∴OF=12,故④正确;
∵,
∴∠ABC≠60°,故②错误.
故答案为:C.
【分析】作出△ABC的外接圆,以AB为斜边在x轴上方作等腰直角三角形ABE,过点E作ED⊥x轴于点D,连接EC,过点E作EF⊥y轴于点F,由垂径定理可得圆心一定在弦的垂直平分线上可判断①;再根据圆周角定理证出点E为△ABNC外接圆的圆心,利用勾股定理求出半径可判断③;判断出四边形EDOF是矩形,得EF=OD=1,ED=OF=5,再在Rt△ECF中利用勾股定理算出CF,可求出OC的长及∠ABC的正切值,从而即可判断②④.
6.【答案】D
【知识点】解直角三角形的应用
【解析】【解答】根据题意可得:
立柱根部与圭表的冬至线的距离为:,
故答案为:D.
【分析】利用正切的定义可得,再求出即可.
7.【答案】D
【知识点】解直角三角形的应用
【解析】【解答】解:如图,过点A作AF⊥BE于点F,过点B作BG⊥CD于点G;
∵AF⊥BE于点F,BG⊥CD于点G,
∴∠AFB=∠BGC=90°,
在Rt△ABF中,,∴,
在Rt△BCG中,,
∴,
∴点A到桌面的最大高度为AF+BG= .
故答案为:D.
【分析】过点A作AF⊥BE于点F,过点B作BG⊥CD于点G;在Rt△ABF中,利用∠ABF的正弦函数可表示出AF,在Rt△BCG中,利用∠BCG的正弦函数可表示出BG,最后根据点A到桌面的最大高度为:AF+BG,可算出答案.
8.【答案】B
【知识点】解直角三角形的应用﹣仰角俯角问题
【解析】【解答】解:在Rt△ABC中,∵∠ABC=90°,
∴,
又∵BC=20米,∠C=37°,
∴AB=BC×tan37°=20tan37°.
故答案为:B.
【分析】在Rt△ABC中,由∠C的正切函数可直接求出AB的长.
9.【答案】B
【知识点】解直角三角形的应用﹣仰角俯角问题
【解析】【解答】解:过点A作AD⊥BC于点D,
由题意可知,∠BAD=30°,∠CAD=60°,
在Rt△ABD中,
,
在Rt△ACD中
,
∴.
故答案为:B
【分析】过点A作AD⊥BC于点D,在Rt△ABD和Rt△ACD中,利用解直角三角形分别求出BD,CD的长,然后根据BC=CD+BD,代入计算求出BC的长.
10.【答案】A
【知识点】勾股定理;矩形的判定与性质;圆周角定理;弧长的计算;相似三角形的判定与性质
【解析】【解答】解:如图1中,连接交于点,连接.
四边形是矩形,,,
四边形是矩形,
,
,
,
,
,,
,
,
,
,
点在为直径的上运动,
当点与重合时,如图2中,连接,.点的运动轨迹是.
此时,,
,
,,
平分,
,
,
点的运动轨迹的长.
故答案为:A.
【分析】连接交于点,连接.证明,利用相似三角形的性质可得PN=2,PM=4,利用勾股定理求出BP=,由垂直的定义可得,可得点在为直径的上运动,当点与重合时,如图2中,连接,.点的运动轨迹是,利用弧长公式计算即可.
11.【答案】1
【知识点】特殊角的三角函数值
12.【答案】75°
【知识点】三角形内角和定理;特殊角的三角函数值;非负数之和为0
【解析】【解答】解:∵,
∴,,
∴,,
∴∠A=60°,∠B=45°,
∴∠C=180°-∠A-∠B=75°,
故答案为:75°.
【分析】根据题意先求出,,再利用特殊角的锐角三角函数值求出∠A=60°,∠B=45°,最后利用三角形的内角和计算求解即可。
13.【答案】48°24′
【知识点】计算器—三角函数
【解析】【解答】解:48°24′.
【分析】根据已知一个角的三角函数值求这个角的算法:先按MODE,选择模式.再键入数字,最后按2ndF和sin或cos,得到这三个角的度数.
14.【答案】6m
【知识点】解直角三角形的应用﹣坡度坡角问题
【解析】【解答】∵河坝横断面迎水坡的坡度为,
∴,
∵,
∴,
在Rt△ABC中,由勾股定理可得:,
故答案为:6.
【分析】先利用坡度比可得,再求出AC的长,最后利用勾股定理求出AB的长即可.
15.【答案】
【知识点】解直角三角形的应用;旋转的性质
【解析】【解答】解:过点B'作B'D⊥AC于点D,如图,
∵将绕点按逆时针方向旋转得到,
∴∠BAB'=90°,
∵∠ABC=90°,
∴BC∥AB',
∴∠B'AD=∠ACB,
在Rt△ABC中,,
,
,
在Rt△AB'D中,
,,
设AD=m,B'D=2m,
∴,
∴,
解得:m=2,
∴AD=2,B'D=4,
∴CD=AC-AD=5-2=3,
在Rt△B'CD中,
B'D=4,CD=3,
∴,
∴.
故答案为: .
【分析】过点B'作B'D⊥AC于点D,由旋转得∠BAB'=90°,因此BC∥AB',得∠B'AD=∠ACB,在Rt△ABC中得AC长和,在Rt△AB'D中,得AD、B'D长,在Rt△B'CD中,求得CD、B'C的长,即可求解.
16.【答案】60
【知识点】解直角三角形的应用
【解析】【解答】解:∵∠B=56°,∠C=45°,∠ADB=∠ADC=90°,BC=BD+CD=100米,
∴BD= ,CD= ,
∴ + =100,
解得AD≈60.
故答案为:60.
【分析】根据已知和三角函数的定义,得到BC=BD+CD的值,求出AD的值.
17.【答案】
【知识点】解直角三角形;正多边形的性质
【解析】【解答】解:如图,设正六边形ABCDEF的中心为O,连接OC、OD,过点O作OG⊥CD于点G,
∵∠COD=,OC=OD,
∴△COD是等边三角形,
又∵OG⊥CD,
∴∠COG=∠COD=30°,CD=2CG=a,OG=b=10mm,
∴CG=tan∠COG×OG=tan30°×10=mm,
∴a=CD=2CG=mm.
故答案为:.
【分析】设该六边形的中心为O,连接OC、OD,过点O作OG⊥CD于点G,由正多边形的中心角求法可得∠COD=60°,由有一个角为60°的等腰三角形是等边三角形得△COD是等边三角形,由等腰三角形的三线合一得∠COG=∠COD=30°,CD=2CG=a,根据正多边形的对称性得OG=b=10mm,从而由∠COG的正切函数可求出CG,此题得解.
18.【答案】75°31′
【知识点】锐角三角函数的定义;计算器—三角函数;近似数及有效数字
【解析】【解答】解:设一个梯子斜靠在墙上,梯子与地面所成锐角为 ,
∵梯子长10米,梯子位于地面上的一端距离墙壁2.5米,
∴ ,
解得: .
故答案为:75°31′.
【分析】设梯子与地面所成锐角为α,根据三角函数的概念可得cosα==,然后利用计算器进行计算即可.
19.【答案】解:原式
,
当时,原式.
【知识点】分式的化简求值;特殊角的三角函数值
【解析】【分析】将括号内通分并利用同分母分式减法法则计算,再将除法转化为乘法,进行约分即可化简,最后利用特殊角三角函数值求出x值,然后代入计算即可.
20.【答案】解:
;
,
;
答:,.
【知识点】三角形内角和定理;含30°角的直角三角形;锐角三角函数的定义
【解析】【分析】
根据三角形内角和定理求出∠B,再运用三角函数求出AC,也可根据含有30度角的直角三角形的性质求出AC。
21.【答案】(1);;60
(2)解:由(1)得:,
∵,
∴.
【知识点】菱形的性质;解直角三角形
【解析】【解答】解:(1)∵,,
∴OA=,OB=1,
∵四边形为菱形,
∴OC=OA=,OB=OD=1,∠BAD=2∠BAO,∠AOB=90°,
∴点C的坐标为(-,0),点D的坐标为(0,-1),
∵tan∠BAO=,
∴∠BAO=30°,
∴∠BAD=2∠BAO=60°,
故答案为:,,60.
【分析】(1)利用菱形的性质求出OC=OA=,OB=OD=1,∠BAD=2∠BAO,∠AOB=90°,可得点C、D的坐标,再利用解直角三角形的性质求出∠BAO=30°,可得∠BAD=2∠BAO=60°;
(2)利用勾股定理求出AB的长,再结合点A、C的坐标求出AC的长即可.
22.【答案】解:由题意得:,
设米,
米,
米,
在中,,
米,
在中,,
米,
,
解得:,
米,
【知识点】解直角三角形的应用﹣仰角俯角问题
【解析】【分析】设米,先求出,再利用解直角三角形的方法可得,,可得,再求出x的值即可.
23.【答案】解:过点作交于,
则米,
在中,有米,
米
故BC米,
答:旗杆的高度约为米.
【知识点】解直角三角形的应用
【解析】【分析】如图,过点D作DE⊥BC于E,在Rt△DEC中,DE=12,tan47°≈1.07,则可求出CE=12.8,再根据BE=1.5,BC=CE+BE即可求解。
24.【答案】(1)解:作于,如图.
在中,,
,
,
,
.
故他上升的高度为米;
(2)解:如图,延长交于点,设,
由题意得,,
,
,
,
在中,,
,
在中,,
.
,
,
解得.
答:大树的高度约为米.
【知识点】解直角三角形的应用﹣仰角俯角问题
【解析】【分析】(1)在直角三角形中,根据勾股定理即可求出答案.
(2)在直角三角形中,根据锐角三角形函数的定义即可求出答案.
25.【答案】(1)解:由题意得:
,
,
在中,米,
米,
无人机的飞行高度为米;
(2)解:过点作,垂足为,
则米,,
在中,,
米,
米,
米,
米,
河流的宽度约为米.
【知识点】平行线的性质;解直角三角形的应用﹣仰角俯角问题
【解析】【分析】(1)根据直线平行性质,可得,在中,解直角三角形即可求出答案。
(2)过点作,垂足为, 可得米,,在中,解直角三角形即可求出答案。
26.【答案】(1)解:在中,米,,
米,
的长为米;
(2)解:由题意得:米,
米,
米,
在中,,
米,
米,
王老师从山脚点到达山顶点共走了约米.
【知识点】含30°角的直角三角形;解直角三角形的应用﹣坡度坡角问题
【解析】【分析】(1)在中,根据含30度角的直角三角形的性质,即可求解;
(2)由题意得:米,在中,,根据正弦的定义求得BC,即可求解.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
