1.1.3 第2课时 补集及其应用 课件(共43张PPT)
文档属性
| 名称 | 1.1.3 第2课时 补集及其应用 课件(共43张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 596.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-25 15:34:43 | ||
图片预览










文档简介
(共43张PPT)
第一章 集合与常用逻辑用语
1.1 集合
1.1.3 集合的基本运算
第2课时 补集及其应用
基础知识
3.补集
情境与问题
如果学校里所有同学组成的集合记为 S,所有男同学组成的集合记为 M,所有女同学组成的集合记为 F,那么:
这三个集合之间有什么联系
(2) 如果x∈S且x M,你能得到什么结论
可以看出,集合 M 和集合 F 都是集合 S 的子集,而且如果x∈S 且x M,则一定有x∈F.
在研究集合与集合之间的关系时,如果所要研究的集合都是某一给定集合的子集,那么称这个给定的集合为全集,全集通常用 U 表示 如果集合 A 是全集 U 的一个子集,则由U 中不属于 A 的所有元素组成的集合,称为 A 在 U 中的补集,记作
UA
读作“A 在U中的补集”,由全集 U 及其子集 A 得到 UA,通常称为补集运算.
集合的补集也可用维恩图形象地表示,其中全集通常用矩形区域代表,如图所示。
因此,上述情境与问题中的集合满足
sF =M
sM =F
例如,如果U={1,2,3,4,5,6},A={1,3,5},则
UA= {2,4,6}
注意,此时 UA仍是U 的一个子集,因此 U ( UA) 也是有意义的,此例中的
U ( UA)= {1,3,5}=A
事实上,给定全集U及其任意一个子集A,补集运算具有如下性质:
(1)A∪( UA) =U;
(2) A∩ ( UA) = ;
(3) UA ( UA) =A.
典例精析
已知U={x∈N | x ≤ 7},A={x∈U | x ≤7},B={x∈U | 0<2x ≤7},求 UA, UB,( UA)∪( UB), U (A∩B).
分析:注意U中的元素都是自然数,而且A,B都是U的子集.
解:不难看出
U={0,1,2,3,4,5,6,7},A={0,1,2},B= {1,2,3}.
因此
UA={3,4,5,6,7}
UB={0,4,5,6,7}
( UA)∪( UB) ={0,3,4,5,6,7}
U (A∩B)={0,3,4,5,6,7}
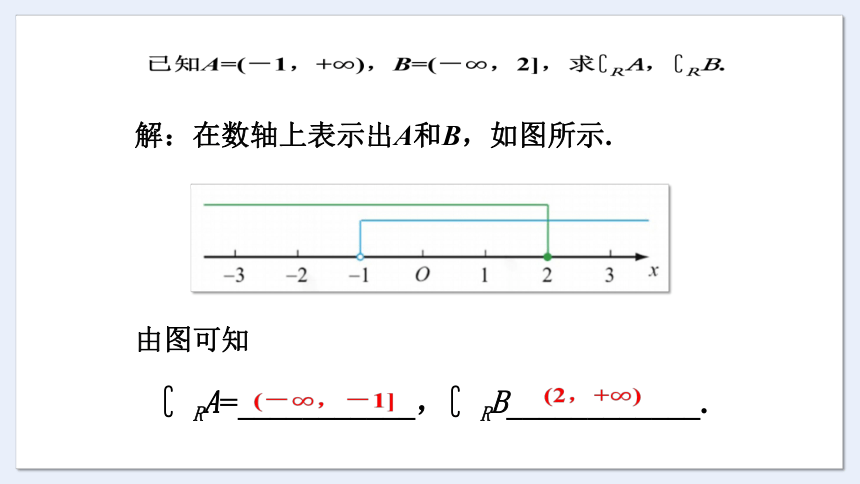
已知A=(-1,+),B=(-,2],求 RA, RB.
解:在数轴上表示出A和B,如图所示.
由图可知
RA=___________, RB____________.
(-,-1]
(2,+)
基础自测
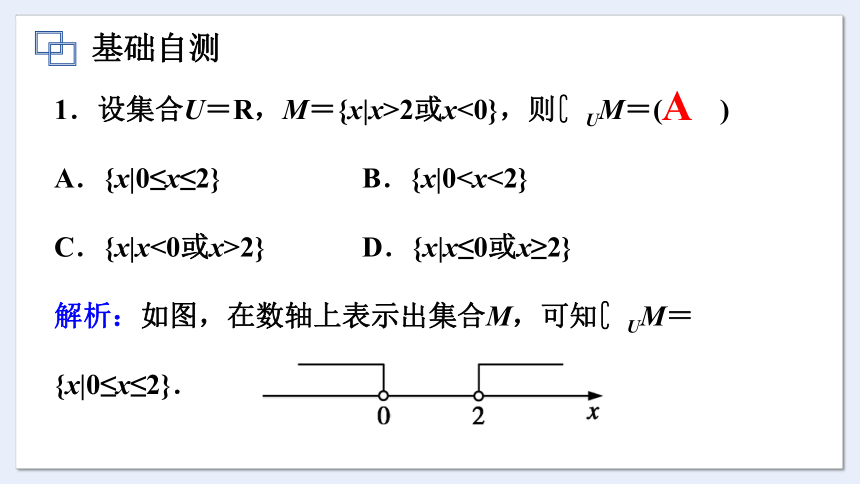
1.设集合U=R,M={x|x>2或x<0},则 UM=( )
A.{x|0≤x≤2} B.{x|0C.{x|x<0或x>2} D.{x|x≤0或x≥2}
解析:如图,在数轴上表示出集合M,可知 UM={x|0≤x≤2}.
A
2.已知全集U={x|-5解析:易知U={-4,-3,-2,-1,0,1,2,3,4},A={0,1,2},故 UA={-4,-3,-2,-1,3,4}.
{-4,-3,-2,-1,3,4}
3.下列说法正确的是___________(填序号).
①全集一定包含任何元素;
②同一个集合在不同的全集中补集不同;
③不同的集合在同一个全集中的补集也不同.
②③
4.若全集U={x∈R|-2≤x≤2},则集合A={x∈R|-2≤x≤0}的补集 UA=______________.
解析:借助数轴易得 UA={x∈R|0{x|05.设全集为U,M={0,2,4}, UM={6},则U=___________.
解析:∵M={0,2,4}, UM={6},∴U={0,2,4,6}.
{0,2,4,6}
补集的运算
典例剖析
已知全集U=R,集合A={x|-3求:(1) UA, UB;
(2) U(A∩B).
思路探究:(1)根据补集的定义,借助于数轴写出;(2)先求A∩B,再根据补集的定义写出。
归纳提升:求集合补集的方法
(1)当集合用列举法表示时,可借助维恩图求解。
(2)当集合是用描述法表示的连续数集时,可借助数轴,利用数轴分析求解。
对点训练
(1)若全集U={0,1,2,3}且 UA={2},则集合A的真子集共有( )
A.3个 B.5个
C.7个 D.8个
(2)已知全集U=[-3,+∞),集合A=(-3,4],则 UA=___________________.
C
{-3}∪(4,+∞)
解析:(1)因为U={0,1,2,3}且 UA={2},所以A={0,1,3},所以集合A的真子集共有7个.
(2)借助数轴得 UA={-3}∪(4,+∞).
交集、并集、补集的综合运算
典例剖析
(1)已知全集U={x|x≤4},集合A={x|-2(2)全集U={x|x<10,x∈N+},A U,B U,( UB)∩A={1,9},A∩B={3},( UA)∩( UB)={4,6,7},求集合A,B.
思路探究:(1)可借助数轴分析求解。(2)将集合用维恩图表示出来,进行观察易写出集合A和B中的元素;也可直接根据集合运算的含义分析求解。
解析:(1)把全集U和集合A,B在数轴上表示(如图所示),
由图可知 UA={x|x≤-2,或3≤x≤4},
A∩B={x|-2 U(A∩B)={x|x≤-2,或3≤x≤4},
( UA)∩B={x|-3(2)方法一:根据题意作出维恩图如图所示.
由图可知A={1,3,9},B={2,3,5,8}.
方法二:∵( UB)∩A={1,9},
( UA)∩( UB)={4,6,7},∴ UB={1,4,6,7,9}.
又U={1,2,3,4,5,6,7,8,9},∴B={2,3,5,8}.
∵( UB)∩A={1,9},A∩B={3}.
∴A={1,3,9}.
归纳提升:解决集合运算问题的方法
1. 解决集合的混合运算问题时,一般先运算括号内的部分,如求( UA)∩B时,先求出 UA,再求交集;求 U(A∪B)时,先求出A∪B,再求补集。
2. 当集合是用列举法表示时(如数集),可以通过列举集合的元素分别得到所求的集合;当集合是用描述法表示时(如区间形式表示的集合),则可运用数轴求解。
对点训练
(1)如图所示,I是全集,M,P,S是I的3个子集,则阴影部分所表示的集合是( )
A.(M∩P)∩S
B.(M∩P)∪S
C.(M∩P)∩ IS
D.(M∩P)∪ IS
(2)已知全集U=(-∞,4],集合A=(-2,3),B=[-3,2],求A∩B,( UA)∪B,A∩( UB),( UA)∪( UB).
C
典例剖析
补集运算中的参数问题
(1)设全集U={2,3,a2+2a-3},A={|2a-1|,2}, UA={5},求实数a的值.
(2)已知集合A={x|x思路探究:解题时要注意对参数取值的检验.(1)中需对a的值是否满足A U进行检验.(2)中要验证“=”能否取到.
a≥2
解析:(1)∵ UA={5},∴5∈U,且5 A,
∴a2+2a-3=5,解得a=2或a=-4.
∴U={2,3,a2+2a-3}={2,3,5}.
当a=2时,A={|2a-1|,2}={3,2},A U,符合题意;
当a=-4时,A={|2a-1|,2}={9,2},A不是U的子集,故舍去.
∴a=2.
(2) RB={x|x≤1,或x≥2},由于A∪ RB=R,如图所示,所以a≥2.
归纳提升:由集合的补集求解参数的方法
(1)有限集:由补集求参数问题,若集合中元素个数有限时,可利用补集定义并结合集合知识求解。
(2)无限集:与集合交、并、补运算有关的求参数问题,若集合中元素有无限个时,一般借助数轴分析求解。
对点训练
设集合A={x|x+m≥0},B={x|-2解析:由已知A={x|x≥-m},得 UA={x|x<-m},
因为B={x|-2所以-m≤-2,即m≥2,
所以m的取值范围是[2,+∞).
补集思想的应用——正难则反
典例剖析
若集合A={x|ax2+3x+2=0}中至多有1个元素,则实数a的取值范围为__________________.
思路探究:若采取分类讨论的方法,所分情况较多,求解比较麻烦,可考虑构造“补集”,然后再利用“补集”的补集求解。
归纳提升:运用补集思想解题的步骤
当从正面考虑情况较多,问题较复杂时,往往考虑运用补集思想。其解题步骤为:
第一步,否定已知条件,考虑反面问题;
第二步,求解反面问题对应的参数范围;
第三步,取反面问题对应的参数范围的“补集”。
对点训练
已知集合A={y|y>a2+1或y解析:因为A={y|y>a2+1或y我们不妨先考虑当A∩B= 时a的取值范围,
在数轴上表示集合A,B,如图所示.
忽视全集
已知集合A={x|x2-4mx+1=0,x∈R},B=(-∞,0),若A∩B≠ ,求实数m的取值范围。
典例剖析
误区警示:当出现“至少”“至多”或正面直接求解情况较多时,我们可以考虑运用补集思想去解决,但必须明确全集是谁,只有正确求出全集,才可能求出补集。
图示法
典例剖析
进行集合的交、并综合运算时,为了保证运算的准确性、有效性、简捷性,通常需要借助Venn图或数轴这两个有力的工具,数形结合来分析得出结果。
一般来说,用列举法表示的数集或者研究比较抽象的集合之间关系时,用Venn图比较方便,如( UA)∩B,( UB)∩A等在图示法中的表示如图所示。
如图所示,两条封闭相交的曲线将集合U分为四个部分:
(1)( UA)∩B;
(2)( UB)∩A;
(3)A∩B;
(4) U(A∪B).
用描述法表示的数集,特别是和不等式相关的集合之间的运算。通常用数轴分析得出结果,这样可以将抽象问题直观化。
已知全集U={x|x∈N,且x是不大于20的素数},M U,N U,且M∩( UN)={3,5},( UM)∩N={7,19},( UM)∩( UN)={2,17},求集合M、N。
解析:用Venn图表示集合U、M、N(如图),将符合条件的元素依次填入图中相应的区域内。由图可知,M={3,5,11,13},N={7,11,13,19}。
完成课后相关练习
谢谢观看
谢谢观看
第一章 集合与常用逻辑用语
1.1 集合
1.1.3 集合的基本运算
第2课时 补集及其应用
基础知识
3.补集
情境与问题
如果学校里所有同学组成的集合记为 S,所有男同学组成的集合记为 M,所有女同学组成的集合记为 F,那么:
这三个集合之间有什么联系
(2) 如果x∈S且x M,你能得到什么结论
可以看出,集合 M 和集合 F 都是集合 S 的子集,而且如果x∈S 且x M,则一定有x∈F.
在研究集合与集合之间的关系时,如果所要研究的集合都是某一给定集合的子集,那么称这个给定的集合为全集,全集通常用 U 表示 如果集合 A 是全集 U 的一个子集,则由U 中不属于 A 的所有元素组成的集合,称为 A 在 U 中的补集,记作
UA
读作“A 在U中的补集”,由全集 U 及其子集 A 得到 UA,通常称为补集运算.
集合的补集也可用维恩图形象地表示,其中全集通常用矩形区域代表,如图所示。
因此,上述情境与问题中的集合满足
sF =M
sM =F
例如,如果U={1,2,3,4,5,6},A={1,3,5},则
UA= {2,4,6}
注意,此时 UA仍是U 的一个子集,因此 U ( UA) 也是有意义的,此例中的
U ( UA)= {1,3,5}=A
事实上,给定全集U及其任意一个子集A,补集运算具有如下性质:
(1)A∪( UA) =U;
(2) A∩ ( UA) = ;
(3) UA ( UA) =A.
典例精析
已知U={x∈N | x ≤ 7},A={x∈U | x ≤7},B={x∈U | 0<2x ≤7},求 UA, UB,( UA)∪( UB), U (A∩B).
分析:注意U中的元素都是自然数,而且A,B都是U的子集.
解:不难看出
U={0,1,2,3,4,5,6,7},A={0,1,2},B= {1,2,3}.
因此
UA={3,4,5,6,7}
UB={0,4,5,6,7}
( UA)∪( UB) ={0,3,4,5,6,7}
U (A∩B)={0,3,4,5,6,7}
已知A=(-1,+),B=(-,2],求 RA, RB.
解:在数轴上表示出A和B,如图所示.
由图可知
RA=___________, RB____________.
(-,-1]
(2,+)
基础自测
1.设集合U=R,M={x|x>2或x<0},则 UM=( )
A.{x|0≤x≤2} B.{x|0
解析:如图,在数轴上表示出集合M,可知 UM={x|0≤x≤2}.
A
2.已知全集U={x|-5
{-4,-3,-2,-1,3,4}
3.下列说法正确的是___________(填序号).
①全集一定包含任何元素;
②同一个集合在不同的全集中补集不同;
③不同的集合在同一个全集中的补集也不同.
②③
4.若全集U={x∈R|-2≤x≤2},则集合A={x∈R|-2≤x≤0}的补集 UA=______________.
解析:借助数轴易得 UA={x∈R|0
解析:∵M={0,2,4}, UM={6},∴U={0,2,4,6}.
{0,2,4,6}
补集的运算
典例剖析
已知全集U=R,集合A={x|-3
(2) U(A∩B).
思路探究:(1)根据补集的定义,借助于数轴写出;(2)先求A∩B,再根据补集的定义写出。
归纳提升:求集合补集的方法
(1)当集合用列举法表示时,可借助维恩图求解。
(2)当集合是用描述法表示的连续数集时,可借助数轴,利用数轴分析求解。
对点训练
(1)若全集U={0,1,2,3}且 UA={2},则集合A的真子集共有( )
A.3个 B.5个
C.7个 D.8个
(2)已知全集U=[-3,+∞),集合A=(-3,4],则 UA=___________________.
C
{-3}∪(4,+∞)
解析:(1)因为U={0,1,2,3}且 UA={2},所以A={0,1,3},所以集合A的真子集共有7个.
(2)借助数轴得 UA={-3}∪(4,+∞).
交集、并集、补集的综合运算
典例剖析
(1)已知全集U={x|x≤4},集合A={x|-2
思路探究:(1)可借助数轴分析求解。(2)将集合用维恩图表示出来,进行观察易写出集合A和B中的元素;也可直接根据集合运算的含义分析求解。
解析:(1)把全集U和集合A,B在数轴上表示(如图所示),
由图可知 UA={x|x≤-2,或3≤x≤4},
A∩B={x|-2
( UA)∩B={x|-3
由图可知A={1,3,9},B={2,3,5,8}.
方法二:∵( UB)∩A={1,9},
( UA)∩( UB)={4,6,7},∴ UB={1,4,6,7,9}.
又U={1,2,3,4,5,6,7,8,9},∴B={2,3,5,8}.
∵( UB)∩A={1,9},A∩B={3}.
∴A={1,3,9}.
归纳提升:解决集合运算问题的方法
1. 解决集合的混合运算问题时,一般先运算括号内的部分,如求( UA)∩B时,先求出 UA,再求交集;求 U(A∪B)时,先求出A∪B,再求补集。
2. 当集合是用列举法表示时(如数集),可以通过列举集合的元素分别得到所求的集合;当集合是用描述法表示时(如区间形式表示的集合),则可运用数轴求解。
对点训练
(1)如图所示,I是全集,M,P,S是I的3个子集,则阴影部分所表示的集合是( )
A.(M∩P)∩S
B.(M∩P)∪S
C.(M∩P)∩ IS
D.(M∩P)∪ IS
(2)已知全集U=(-∞,4],集合A=(-2,3),B=[-3,2],求A∩B,( UA)∪B,A∩( UB),( UA)∪( UB).
C
典例剖析
补集运算中的参数问题
(1)设全集U={2,3,a2+2a-3},A={|2a-1|,2}, UA={5},求实数a的值.
(2)已知集合A={x|x
a≥2
解析:(1)∵ UA={5},∴5∈U,且5 A,
∴a2+2a-3=5,解得a=2或a=-4.
∴U={2,3,a2+2a-3}={2,3,5}.
当a=2时,A={|2a-1|,2}={3,2},A U,符合题意;
当a=-4时,A={|2a-1|,2}={9,2},A不是U的子集,故舍去.
∴a=2.
(2) RB={x|x≤1,或x≥2},由于A∪ RB=R,如图所示,所以a≥2.
归纳提升:由集合的补集求解参数的方法
(1)有限集:由补集求参数问题,若集合中元素个数有限时,可利用补集定义并结合集合知识求解。
(2)无限集:与集合交、并、补运算有关的求参数问题,若集合中元素有无限个时,一般借助数轴分析求解。
对点训练
设集合A={x|x+m≥0},B={x|-2
因为B={x|-2
所以m的取值范围是[2,+∞).
补集思想的应用——正难则反
典例剖析
若集合A={x|ax2+3x+2=0}中至多有1个元素,则实数a的取值范围为__________________.
思路探究:若采取分类讨论的方法,所分情况较多,求解比较麻烦,可考虑构造“补集”,然后再利用“补集”的补集求解。
归纳提升:运用补集思想解题的步骤
当从正面考虑情况较多,问题较复杂时,往往考虑运用补集思想。其解题步骤为:
第一步,否定已知条件,考虑反面问题;
第二步,求解反面问题对应的参数范围;
第三步,取反面问题对应的参数范围的“补集”。
对点训练
已知集合A={y|y>a2+1或y
在数轴上表示集合A,B,如图所示.
忽视全集
已知集合A={x|x2-4mx+1=0,x∈R},B=(-∞,0),若A∩B≠ ,求实数m的取值范围。
典例剖析
误区警示:当出现“至少”“至多”或正面直接求解情况较多时,我们可以考虑运用补集思想去解决,但必须明确全集是谁,只有正确求出全集,才可能求出补集。
图示法
典例剖析
进行集合的交、并综合运算时,为了保证运算的准确性、有效性、简捷性,通常需要借助Venn图或数轴这两个有力的工具,数形结合来分析得出结果。
一般来说,用列举法表示的数集或者研究比较抽象的集合之间关系时,用Venn图比较方便,如( UA)∩B,( UB)∩A等在图示法中的表示如图所示。
如图所示,两条封闭相交的曲线将集合U分为四个部分:
(1)( UA)∩B;
(2)( UB)∩A;
(3)A∩B;
(4) U(A∪B).
用描述法表示的数集,特别是和不等式相关的集合之间的运算。通常用数轴分析得出结果,这样可以将抽象问题直观化。
已知全集U={x|x∈N,且x是不大于20的素数},M U,N U,且M∩( UN)={3,5},( UM)∩N={7,19},( UM)∩( UN)={2,17},求集合M、N。
解析:用Venn图表示集合U、M、N(如图),将符合条件的元素依次填入图中相应的区域内。由图可知,M={3,5,11,13},N={7,11,13,19}。
完成课后相关练习
谢谢观看
谢谢观看
