1.1.1 变化率问题 课件(苏教版选修2-2)
文档属性
| 名称 | 1.1.1 变化率问题 课件(苏教版选修2-2) |

|
|
| 格式 | zip | ||
| 文件大小 | 933.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-14 00:00:00 | ||
图片预览


文档简介
课件19张PPT。业精于勤,荒于嬉,行成于思,毁于随。 学 而 不 思 则 罔, 思 而 不 学 则 殆。 成绩=勤奋的学习+正确的方法+少谈空话博学之,审问之,慎思之,明辨之,笃行之。 自觉、自律、自信、自强 !第一章 导数及其应用1.1.1 平均变化率 深圳市建文中学
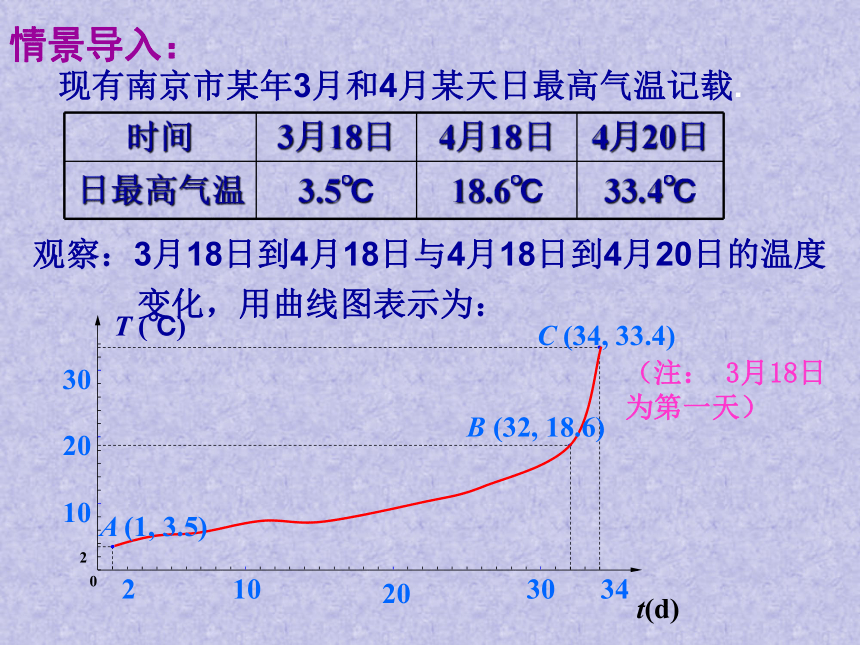
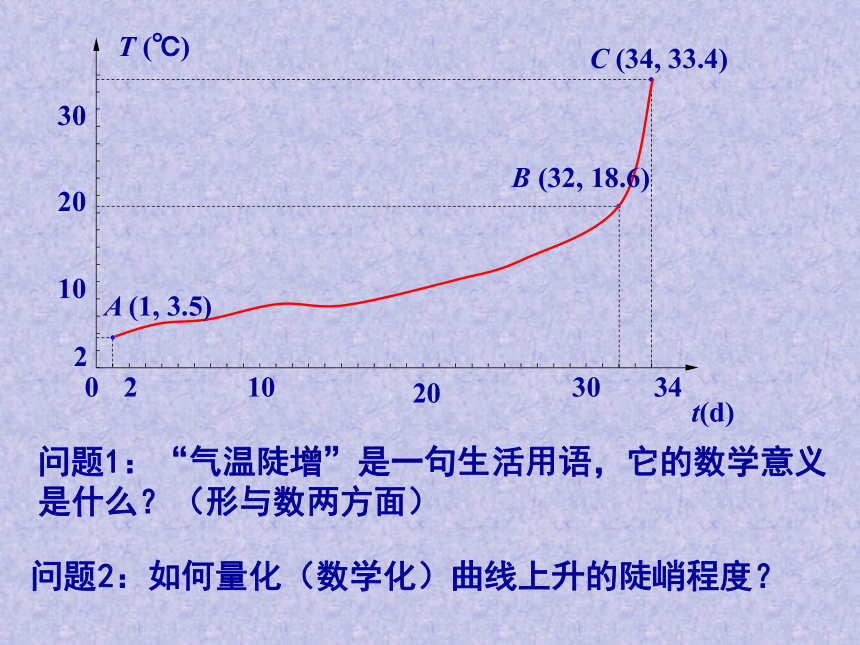
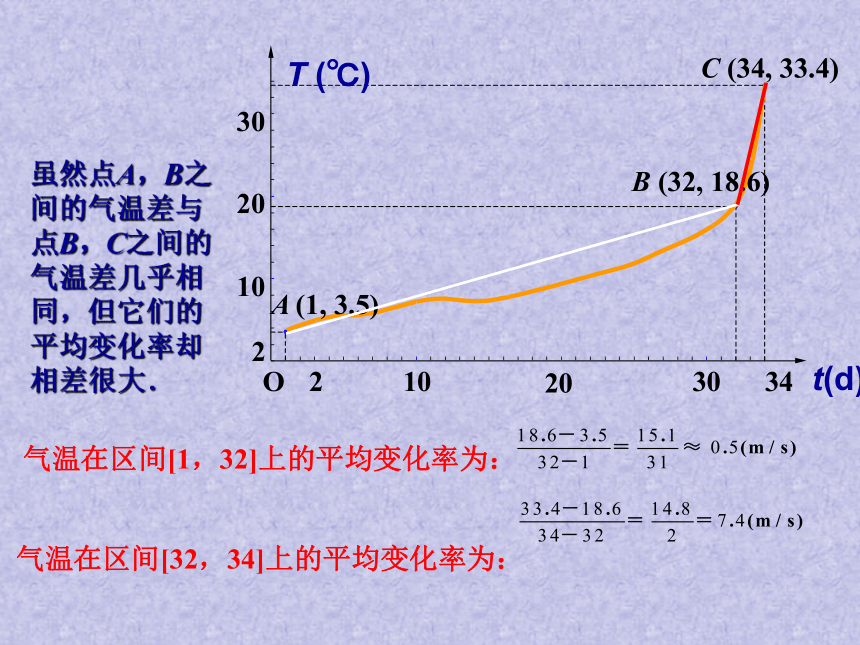
高中数学老师欧阳文丰现有南京市某年3月和4月某天日最高气温记载.观察:3月18日到4月18日与4月18日到4月20日的温度变化,用曲线图表示为:(注: 3月18日为第一天)情景导入:问题1:“气温陡增”是一句生活用语,它的数学意义
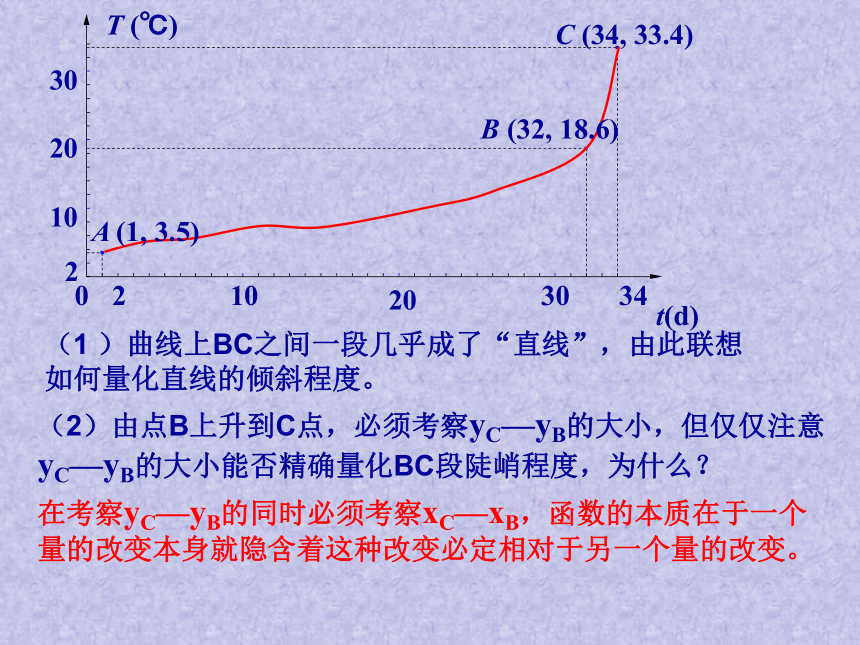
是什么?(形与数两方面)问题2:如何量化(数学化)曲线上升的陡峭程度?(1 )曲线上BC之间一段几乎成了“直线”,由此联想如何量化直线的倾斜程度。(2)由点B上升到C点,必须考察yC—yB的大小,但仅仅注意
yC—yB的大小能否精确量化BC段陡峭程度,为什么?在考察yC—yB的同时必须考察xC—xB,函数的本质在于一个
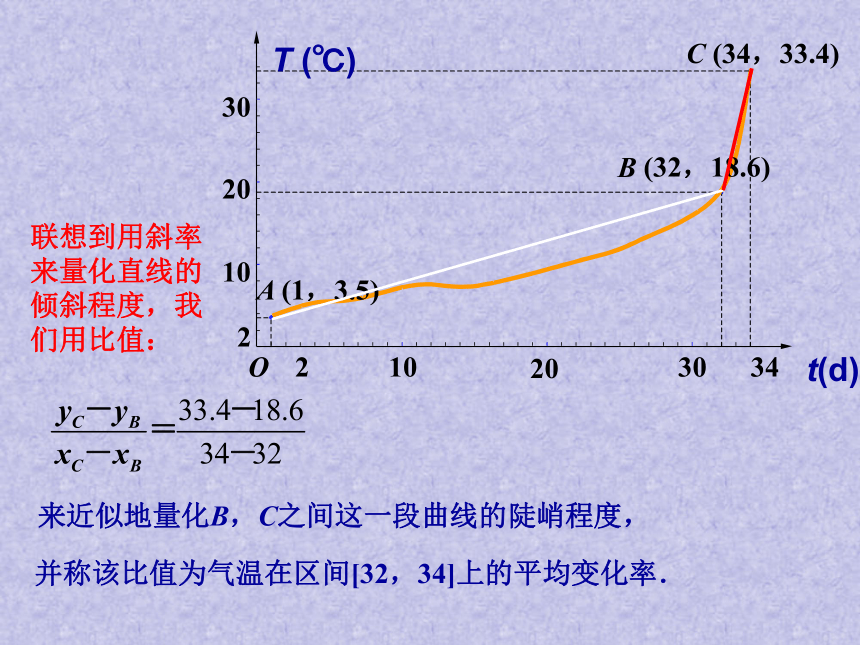
量的改变本身就隐含着这种改变必定相对于另一个量的改变。 t(d)2030 342 10 20 30 A (1,3.5) B (32,18.6) OC (34,33.4) T (℃)
2 10联想到用斜率来量化直线的倾斜程度,我们用比值:来近似地量化B,C之间这一段曲线的陡峭程度,并称该比值为气温在区间[32,34]上的平均变化率.2030 342 10 20 30 A (1, 3.5) B (32, 18.6) OC (34, 33.4)T (℃) 2 10气温在区间[1,32]上的平均变化率为:气温在区间[32,34]上的平均变化率为:虽然点A,B之间的气温差与点B,C之间的气温差几乎相同,但它们的平均变化率却相差很大. t(d)一般地,函数f(x)在区间[x1,x2]上的平均变化率为 建构数学注意:不能脱离区间而言定义:平均变化率: 式子 称为函数 f (x)从x1到 x2的平均变化率.令△x = x2 – x1 , △ y = f (x2) – f (x1) ,则关于平均变化率的理解思考:观察函数f(x)的图象
平均变化率
表示什么?OABxyY=f(x)x1x2f(x1)f(x2)x2-x1f(x2)-f(x1)直线AB的斜率例1 某婴儿从出生到第12个月的体重变化如图所示,试分别计算从出生到第3个月与第6个月到第12个月该婴儿体重的平均变化率.数学运用平均变化率: 解 从出生到第3个月,婴儿体重平均变化率为从第6个月到第12个月,婴儿体重平均变化率为不同的区间上平均变化率可能不同(kg/月)(kg/月)例2 水经过虹吸管从容器甲中流向容器乙,t s后容器甲中水的体积V(t)=5×2-0.1t(单位:cm3),试计算第一个10s内V的平均变化率.问题1 例2中的平均变化率的实际意义是什么?解 在第一个10s内,体积V的平均变化率为平均变化率可正可负问题2 负号表示容器甲中的水在减少,但是否表示10秒内每一时刻容器甲中水的体积减少的速度呢? 甲乙问题3 乙容器中水的体积平均变化率为多少?甲乙解 在第一个10s内,体积V的平均变化率为例2 水经过虹吸管从容器甲中流向容器乙,t s后容器甲中水的体积V(t)=5×2-0.1t(单位:cm3),试计算第一个10s内V的平均变化率.例3 已知函数 ,分别计算 在下列区间上的平均变化率: (1)[1,3];
(2)[1,2];
(3)[1,1.1];
(4)[1,1.001];例4 已知函数f(x)=2x+1,g(x)=-2x, 分别计算在区间[-3,-1],[0,5]上f(x)及g(x)的平均变化率. 你在解本题的过程中有没有发现什么?一次函数y=kx+b在区间[m,n]上的平均变化率等于斜率k.ABx1x2f(x1)f(x2)△x△y你能解释为什么会出现这一现象吗?小结:1.函数的平均变化率2.求函数的平均变化率的步骤:
(1)求函数的增量Δf=Δy=f(x2)-f(x1);
(2)计算平均变化率
课后作业预习第1.1.2节瞬时变化率----导数.2. 课本P7 练习1---5;P16 习题1.1 第1题.
高中数学老师欧阳文丰现有南京市某年3月和4月某天日最高气温记载.观察:3月18日到4月18日与4月18日到4月20日的温度变化,用曲线图表示为:(注: 3月18日为第一天)情景导入:问题1:“气温陡增”是一句生活用语,它的数学意义
是什么?(形与数两方面)问题2:如何量化(数学化)曲线上升的陡峭程度?(1 )曲线上BC之间一段几乎成了“直线”,由此联想如何量化直线的倾斜程度。(2)由点B上升到C点,必须考察yC—yB的大小,但仅仅注意
yC—yB的大小能否精确量化BC段陡峭程度,为什么?在考察yC—yB的同时必须考察xC—xB,函数的本质在于一个
量的改变本身就隐含着这种改变必定相对于另一个量的改变。 t(d)2030 342 10 20 30 A (1,3.5) B (32,18.6) OC (34,33.4) T (℃)
2 10联想到用斜率来量化直线的倾斜程度,我们用比值:来近似地量化B,C之间这一段曲线的陡峭程度,并称该比值为气温在区间[32,34]上的平均变化率.2030 342 10 20 30 A (1, 3.5) B (32, 18.6) OC (34, 33.4)T (℃) 2 10气温在区间[1,32]上的平均变化率为:气温在区间[32,34]上的平均变化率为:虽然点A,B之间的气温差与点B,C之间的气温差几乎相同,但它们的平均变化率却相差很大. t(d)一般地,函数f(x)在区间[x1,x2]上的平均变化率为 建构数学注意:不能脱离区间而言定义:平均变化率: 式子 称为函数 f (x)从x1到 x2的平均变化率.令△x = x2 – x1 , △ y = f (x2) – f (x1) ,则关于平均变化率的理解思考:观察函数f(x)的图象
平均变化率
表示什么?OABxyY=f(x)x1x2f(x1)f(x2)x2-x1f(x2)-f(x1)直线AB的斜率例1 某婴儿从出生到第12个月的体重变化如图所示,试分别计算从出生到第3个月与第6个月到第12个月该婴儿体重的平均变化率.数学运用平均变化率: 解 从出生到第3个月,婴儿体重平均变化率为从第6个月到第12个月,婴儿体重平均变化率为不同的区间上平均变化率可能不同(kg/月)(kg/月)例2 水经过虹吸管从容器甲中流向容器乙,t s后容器甲中水的体积V(t)=5×2-0.1t(单位:cm3),试计算第一个10s内V的平均变化率.问题1 例2中的平均变化率的实际意义是什么?解 在第一个10s内,体积V的平均变化率为平均变化率可正可负问题2 负号表示容器甲中的水在减少,但是否表示10秒内每一时刻容器甲中水的体积减少的速度呢? 甲乙问题3 乙容器中水的体积平均变化率为多少?甲乙解 在第一个10s内,体积V的平均变化率为例2 水经过虹吸管从容器甲中流向容器乙,t s后容器甲中水的体积V(t)=5×2-0.1t(单位:cm3),试计算第一个10s内V的平均变化率.例3 已知函数 ,分别计算 在下列区间上的平均变化率: (1)[1,3];
(2)[1,2];
(3)[1,1.1];
(4)[1,1.001];例4 已知函数f(x)=2x+1,g(x)=-2x, 分别计算在区间[-3,-1],[0,5]上f(x)及g(x)的平均变化率. 你在解本题的过程中有没有发现什么?一次函数y=kx+b在区间[m,n]上的平均变化率等于斜率k.ABx1x2f(x1)f(x2)△x△y你能解释为什么会出现这一现象吗?小结:1.函数的平均变化率2.求函数的平均变化率的步骤:
(1)求函数的增量Δf=Δy=f(x2)-f(x1);
(2)计算平均变化率
课后作业预习第1.1.2节瞬时变化率----导数.2. 课本P7 练习1---5;P16 习题1.1 第1题.
