人教版八年级上册13.4 课题学习 最短路径问题 教学设计
文档属性
| 名称 | 人教版八年级上册13.4 课题学习 最短路径问题 教学设计 |  | |
| 格式 | docx | ||
| 文件大小 | 36.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-26 16:17:08 | ||
图片预览

文档简介
《最短路径问题》教学设计
教材分析
本节课是八年级上册第三章的最后一节内容,是在学习了轴对称的知识后学 习的与实际问题密切相关的最短路径问题,体现了数学知识在实际生活中的作 用。
学情分析
八年级学生总的来说观察、操作、猜想的能力较强,具有一定的探究精神和 合作意识,但灵活运用数学知识解决实际问题的能力较薄弱,说理上还不规范, 几何演绎推理能力有待加强。他们虽然已经学习了“两点之问,线段最短 ”、“垂 线段最短 ”以及轴对称和垂直平分线的性质等相关知识,但由于学习态度和学习 能力的差异导致学习的效果差异也很大,后进生面大。加上他们此前并未接触过 最短问题,数学经验不足,特别是实际问题中最短问题,比较陌生。
教学目标
能利用轴对称解决简单的最短路径问题,体会图形的变化在解决最值问题中 的作用,感悟转化思想.
教学重点
利用轴对称将最短路径问题转化为“两点之间,线段最短 ”问题.
教学难点
如何利用轴对称将最短路径问题转化为线段和最小问题。
教学过程
一、情境导入
1.看视频,然后回答问题:
人们为什么常常违规横穿马路?你能用学过的数学知识解释这一现象吗? (学生回答后借机进行安全教育)
2.这类问题,就是我们今天要研究的“最短路径 ”问题。
二、探索新知
1.将军饮马问题
传说,古希腊亚历山大里亚城里有一位久负盛名的学者,名叫海伦.有一天, 一位将军专程拜访海伦,求教一个百思不得其解的问题:
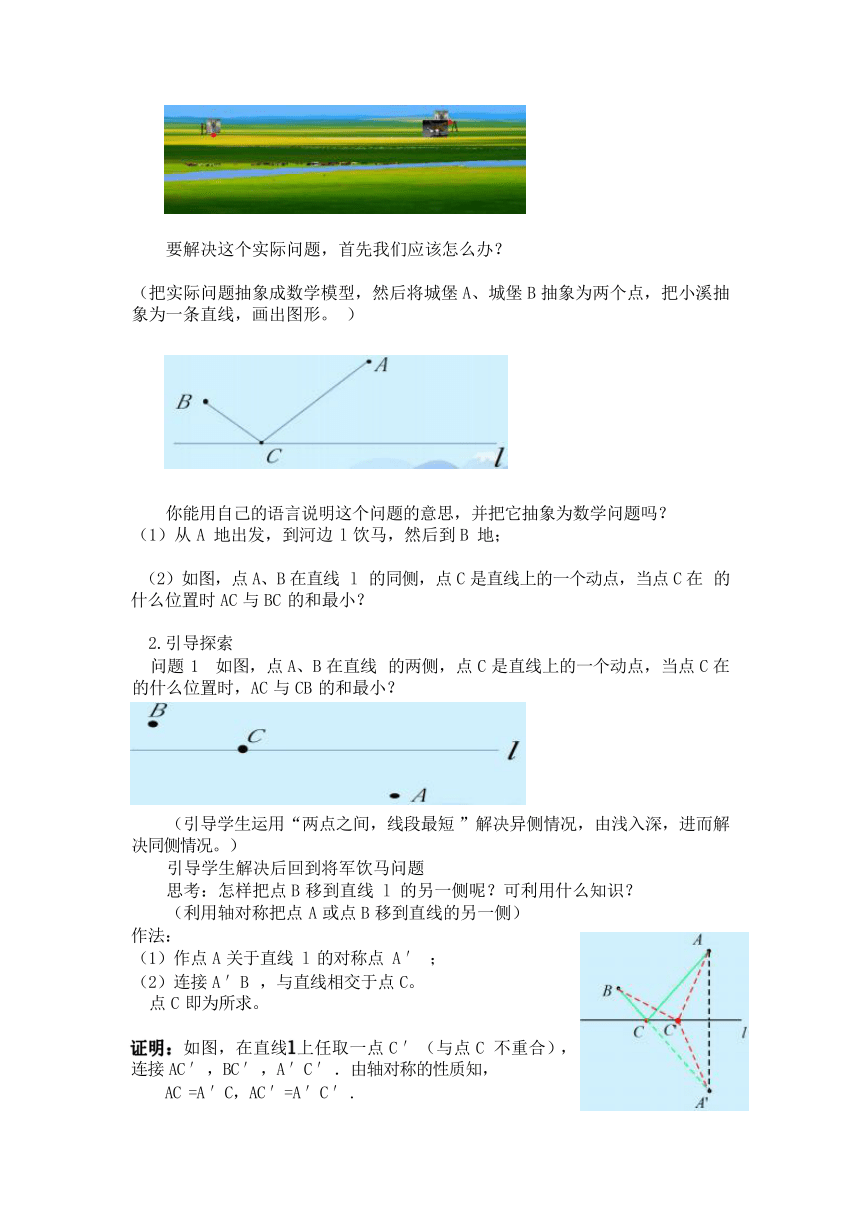
看图:将军每天骑马从城堡 A 到城堡 B,途中马要到小溪边饮水一次,到小 溪什么地方饮马可使他所走的路线全最短?
要解决这个实际问题,首先我们应该怎么办?
(把实际问题抽象成数学模型,然后将城堡 A、城堡 B 抽象为两个点,把小溪抽 象为一条直线,画出图形。 )
你能用自己的语言说明这个问题的意思,并把它抽象为数学问题吗? (1)从 A 地出发,到河边 l 饮马,然后到 B 地;
(2)如图,点 A、B 在直线 l 的同侧,点 C 是直线上的一个动点,当点 C 在 的 什么位置时 AC 与 BC 的和最小?
2.引导探索
问题 1 如图,点 A、B 在直线 的两侧,点 C 是直线上的一个动点,当点 C 在 的什么位置时,AC 与 CB 的和最小?
(引导学生运用“两点之间,线段最短 ”解决异侧情况,由浅入深,进而解 决同侧情况。)
引导学生解决后回到将军饮马问题
思考:怎样把点 B 移到直线 l 的另一侧呢?可利用什么知识?
(利用轴对称把点 A 或点 B 移到直线的另一侧)
作法:
(1)作点 A 关于直线 l 的对称点 A ′ ;
(2)连接 A ′B ,与直线相交于点 C。
点 C 即为所求。
证明:如图,在直线l上任取一点 C ′(与点 C 不重合),
连接 AC ′ ,BC ′ ,A ′C ′ .由轴对称的性质知,
AC =A ′C,AC ′=A ′C ′ .
∴ AC +BC= A ′C +BC = A ′B,
AC ′+BC ′= A ′C ′+BC ′ .
在△A ′BC ′ 中,
A ′B<A ′C ′+BC ′,
∴ AC +BC<AC ′+BC ′ .
即 AC +BC 最短.
问:
证明 AC +BC 最短时,为什么要在直线 l 上任取一点 C ′(与点 C 不重合), 证明 AC +BC <AC ′+BC ′ ?这里的“C ′” 的作用是什么?
(若直线 l 上任意一点(与点 C 不重合)与 A,B 两点的距离和都大于 AC+BC, 就说明 AC + BC 最小. )
三、类比练习
1、已知:P、Q 是 ABC 边 AB、AC 上的点,你能在 BC 上确定一个点 R,使 PQR
的周长最短吗?
2、如图:A 为马厩,B 为帐篷,将军某一天要从马厩牵出马,先到草地边某
一处牧马,再到河边饮马,然后回到帐篷,请你帮他确定这一天的最短路线。
归纳总结:
在解决这一类问题时,我们要善于根据“两点之间,线段最短 ”作定点关于 动点所在直线的对称点将所求线段之和转变为一条线段,从而得出方案或结果。
四、课堂小结
同学们谈谈这节课运用了哪些数学知识,你们学到了什么?
(利用轴对称解决两点之间最短路径问题)
五、布置作业
1.ABC 边 BC 上的点 P,在 AB 边上找一个点 Q,在 AC 边上找一个点 R,构成 △PQR ,使△PQR 的周长最短。
2.已知平面直角坐标系中两点 A(-1,3)、B(-3,1),在 x、y 轴上分别找一点 C、D,使四边形 ABCD 周长最小.
教材分析
本节课是八年级上册第三章的最后一节内容,是在学习了轴对称的知识后学 习的与实际问题密切相关的最短路径问题,体现了数学知识在实际生活中的作 用。
学情分析
八年级学生总的来说观察、操作、猜想的能力较强,具有一定的探究精神和 合作意识,但灵活运用数学知识解决实际问题的能力较薄弱,说理上还不规范, 几何演绎推理能力有待加强。他们虽然已经学习了“两点之问,线段最短 ”、“垂 线段最短 ”以及轴对称和垂直平分线的性质等相关知识,但由于学习态度和学习 能力的差异导致学习的效果差异也很大,后进生面大。加上他们此前并未接触过 最短问题,数学经验不足,特别是实际问题中最短问题,比较陌生。
教学目标
能利用轴对称解决简单的最短路径问题,体会图形的变化在解决最值问题中 的作用,感悟转化思想.
教学重点
利用轴对称将最短路径问题转化为“两点之间,线段最短 ”问题.
教学难点
如何利用轴对称将最短路径问题转化为线段和最小问题。
教学过程
一、情境导入
1.看视频,然后回答问题:
人们为什么常常违规横穿马路?你能用学过的数学知识解释这一现象吗? (学生回答后借机进行安全教育)
2.这类问题,就是我们今天要研究的“最短路径 ”问题。
二、探索新知
1.将军饮马问题
传说,古希腊亚历山大里亚城里有一位久负盛名的学者,名叫海伦.有一天, 一位将军专程拜访海伦,求教一个百思不得其解的问题:
看图:将军每天骑马从城堡 A 到城堡 B,途中马要到小溪边饮水一次,到小 溪什么地方饮马可使他所走的路线全最短?
要解决这个实际问题,首先我们应该怎么办?
(把实际问题抽象成数学模型,然后将城堡 A、城堡 B 抽象为两个点,把小溪抽 象为一条直线,画出图形。 )
你能用自己的语言说明这个问题的意思,并把它抽象为数学问题吗? (1)从 A 地出发,到河边 l 饮马,然后到 B 地;
(2)如图,点 A、B 在直线 l 的同侧,点 C 是直线上的一个动点,当点 C 在 的 什么位置时 AC 与 BC 的和最小?
2.引导探索
问题 1 如图,点 A、B 在直线 的两侧,点 C 是直线上的一个动点,当点 C 在 的什么位置时,AC 与 CB 的和最小?
(引导学生运用“两点之间,线段最短 ”解决异侧情况,由浅入深,进而解 决同侧情况。)
引导学生解决后回到将军饮马问题
思考:怎样把点 B 移到直线 l 的另一侧呢?可利用什么知识?
(利用轴对称把点 A 或点 B 移到直线的另一侧)
作法:
(1)作点 A 关于直线 l 的对称点 A ′ ;
(2)连接 A ′B ,与直线相交于点 C。
点 C 即为所求。
证明:如图,在直线l上任取一点 C ′(与点 C 不重合),
连接 AC ′ ,BC ′ ,A ′C ′ .由轴对称的性质知,
AC =A ′C,AC ′=A ′C ′ .
∴ AC +BC= A ′C +BC = A ′B,
AC ′+BC ′= A ′C ′+BC ′ .
在△A ′BC ′ 中,
A ′B<A ′C ′+BC ′,
∴ AC +BC<AC ′+BC ′ .
即 AC +BC 最短.
问:
证明 AC +BC 最短时,为什么要在直线 l 上任取一点 C ′(与点 C 不重合), 证明 AC +BC <AC ′+BC ′ ?这里的“C ′” 的作用是什么?
(若直线 l 上任意一点(与点 C 不重合)与 A,B 两点的距离和都大于 AC+BC, 就说明 AC + BC 最小. )
三、类比练习
1、已知:P、Q 是 ABC 边 AB、AC 上的点,你能在 BC 上确定一个点 R,使 PQR
的周长最短吗?
2、如图:A 为马厩,B 为帐篷,将军某一天要从马厩牵出马,先到草地边某
一处牧马,再到河边饮马,然后回到帐篷,请你帮他确定这一天的最短路线。
归纳总结:
在解决这一类问题时,我们要善于根据“两点之间,线段最短 ”作定点关于 动点所在直线的对称点将所求线段之和转变为一条线段,从而得出方案或结果。
四、课堂小结
同学们谈谈这节课运用了哪些数学知识,你们学到了什么?
(利用轴对称解决两点之间最短路径问题)
五、布置作业
1.ABC 边 BC 上的点 P,在 AB 边上找一个点 Q,在 AC 边上找一个点 R,构成 △PQR ,使△PQR 的周长最短。
2.已知平面直角坐标系中两点 A(-1,3)、B(-3,1),在 x、y 轴上分别找一点 C、D,使四边形 ABCD 周长最小.
