3.1.2 第1课时 单调性的定义与证明 课件(共45张PPT)
文档属性
| 名称 | 3.1.2 第1课时 单调性的定义与证明 课件(共45张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 954.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-25 18:57:16 | ||
图片预览









文档简介
(共45张PPT)
第三章 函数
3.1 函数的概念与性质
3.1.2 函数的单调性
第1课时 单调性的定义与证明
基础知识
情境与问题
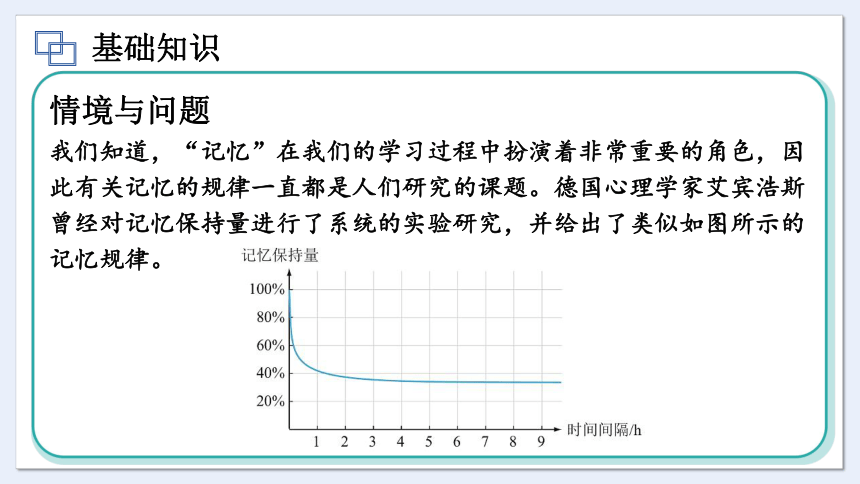
我们知道,“记忆”在我们的学习过程中扮演着非常重要的角色,因此有关记忆的规律一直都是人们研究的课题。德国心理学家艾宾浩斯曾经对记忆保持量进行了系统的实验研究,并给出了类似如图所示的记忆规律。
如果我们以 x 表示时间间隔 (单位: h),y 表示记忆保持量,则不难看出,上图中,y是x的函数,记这个函数为 y=f(x)。
这个函数反映出记忆具有什么规律 你能从中得到什么启发
情境与问题中的函数 y=f (x) 反映出记忆的如下规律:随着时间间隔x的增大,记忆保持量 y 将减小。
给定一个函数,人们有时候关心的是,函数值会随着自变量增大而怎样变化,类似的内容我们在初中曾经接触过。
如图,从正比例函数y=2x的图象可以看出,当自变量由小变大时,这个函数的函数值逐渐变大,即 y 随着 x 的增大而增大;从反比例函数 y=的图象可以看出,在(-∞,0)和(0,+∞)內,这个函数的函数值 y 都随着 x 的增大而减小。
一般地,设函数y=f(x)的定义域为 D,且ID:
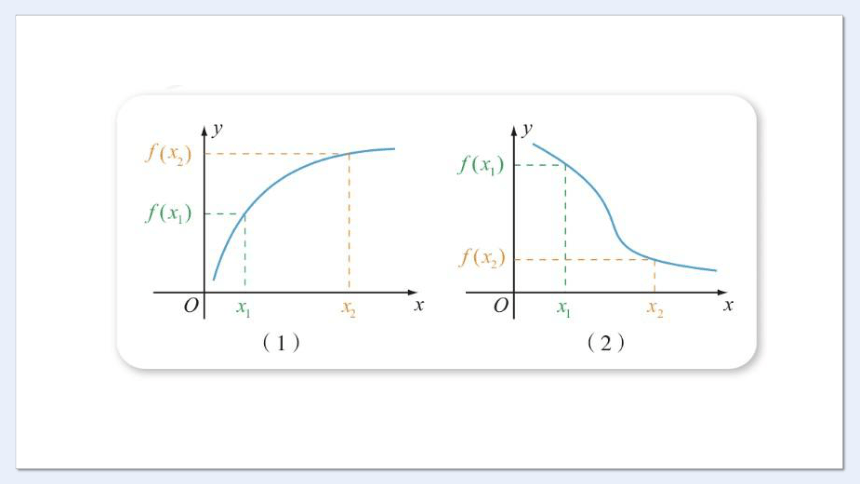
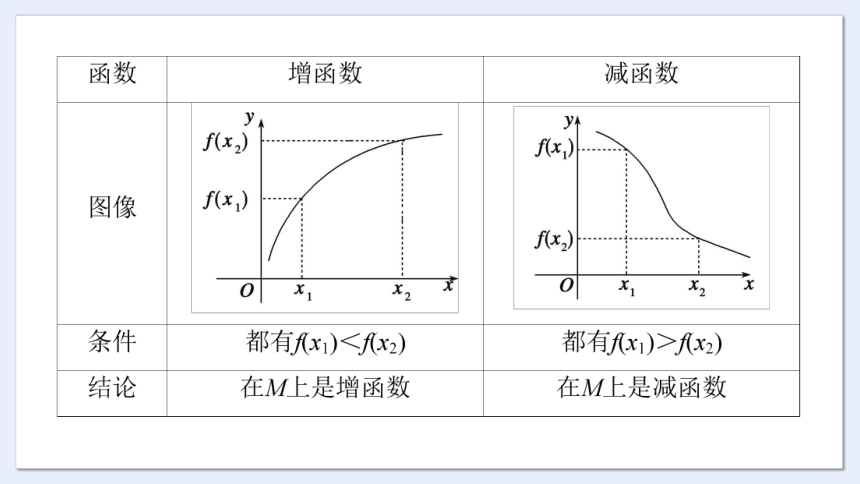
如果对任意 x1,x2∈I,当x1<x2时,都有 f(x1)<f (x2),则称y=f(x)在I上是增函数 (也称在I上单调递增),如图(1)所示;
(2)如果对任意 x1,x2∈I,当x1<x2时,都有f(x1)>f(x2),则称
y=f(x)在I上是减函数 (也称在I上单调递减),如图(2)所示。
两种情况下,都称函数在I上具有单调性 (当I为区间时,称I为函数的单调区间,也可分别称为单调递增区间或单调递减区间)。
由增函数和减函数的定义可知,前面给出的例子中,y=2x在R上是增函数;y=在(-∞,0) 上是减函数,在 (0,+∞)上也是减函数。
尝试与发现
如图所示的函数 y=f(x),在[-6,-4] 上是增函数,在 [-4,-2] 上是减函数,在 [-2,1] 上是__________函数,在 [1,3] 上是__________函数,在 [3,6]上是__________函数。
增
增
减
由尝试与发现可知,从函数的图象能方便地看出函数的单调性。但一般情况下,得到函数的图象并不容易,而且手工作出的图象往往都不精确,因此我们要探讨怎样从函数的解析式来证明函数的单调性。这可以利用函数单调性的定义和不等式的证明方法。
思考1:若把增、减函数定义中的“任意x1,x2”改为“存在x1,x2”可以吗?
提示:不可以,如图:
思考2:“函数f(x)的单调增(减)区间是D”与“函数f(x)在区间D上是增(减)函数”是否相同?
提示:不相同。函数f(x)的单调增(减)区间是D,这一说法意味着除D之外,函数f(x)再无其他单调增(减)区间。
函数f(x)在区间D上是增(减)函数,则意味着区间D是函数f(x)的单调增(减)区间的子区间,即除区间D外,函数f(x)还可能有其他的单调增(减)区间。
典例精析
求证:函数 f(x)= -2x 在 R 上是减函数。
证明:任取x1,x2∈R且x1<x2,则x1-x2<0,那么f(x1)-f(x2)=(-2x1)-(-2x2)=2(x2-x1)>0,
从而 f(x1)>f(x2)。
因此,函数 f(x)=-2x 在 R上是减函数。
一般地,设函数 f(x)的定义域为 D,且x0∈D,如果对任意x∈D,都有f(x)≤f(x0),则称f(x)的最大值为 f(x0),而x0称为 f(x)的最大值点;如果对任意 x∈D,都有 f(x)≥f(x0),则称f(x)的最小值为f(x0),而x0称为 f(x)的最小值点。最大值和最小值统称为最值,最大值点和最小值点统称为最值点。
不难看出,如果函数有最值而且函数的单调性容易求出,则可利用函数的单调性求出函数的最值点和最值。
判断函数 f(x)=3x+5,x∈[-1,6] 的单调性,并求这个函数的最值。
典例精析
解:任取x1,x2∈[-1,6]且x1所以这个函数是_________函数。
因此,当-1≤x≤6 时,有
f(-1) ≤ f(x) ≤ f(6),
从而这个函数的最小值为 f(-1)=_______,最大值为 f(6)= _______。
结论也可由不等式的知识得到:因为-1 ≤ x ≤ 6,所以
-3≤3x≤18,2≤3x+5≤23,
即 f(-1) ≤ f(x) ≤ f(6),其余同上。
增
2
23
基础自测
1.函数f(x)=2在[-2,4]上的单调性为( )
A.减函数 B.增函数
C.先减后增 D.不具有单调性
解析:当x∈[-2,4]时,f(x)的值恒等于2,故函数f(x)=2在[-2,4]上不具有单调性.
D
2.对于函数y=f(x),在给定区间内有两个值x1、x2,且x1A.一定是增函数 B.一定是减函数
C.可能是常数函数 D.单调性不能确定
解析:由函数单调性的定义可知,判断单调性时不能用特殊值代替任意值,故选D。
D
3.函数y=f(x)的图像如图所示,其增区间是___________.
4.函数f(x)=-x2-2x的单调递增区间是______________.
解析:f(x)=-(x+1)2+1,函数f(x)的对称轴为x=-1,故函数的递增区间为(-∞,-1].
[-3,1]
(-∞,-1]
5.若y=(2k-1)x+b是R上的减函数,则k的取值范围为_________,b的取值范围为____.
R
典例剖析
求函数的单调区间
已知x∈R,函数f(x)=x|x-2|,试画出y=f(x)的图像,并结合图像写出函数的单调区间。
思路探究:首先分类讨论,去掉绝对值号,将函数化为分段函数,然后画出图像求解即可。
归纳提升:1.作出函数的图像,利用图形的直观性能快速判断函数的单调区间,但要注意图像一定要画准确。
2.函数的单调区间是函数定义域的子集,在求解的过程中不要忽略了函数的定义域。
3.一个函数出现两个或两个以上的单调区间时,不能用“∪”连接两个单调区间,而要用“和”或“,”连接。
对点训练
(1)如图是定义在区间[-2,2]的函数y=f(x),则f(x)的单调递减区间是___________.
(2)函数f(x)=x|x|-2x的单调递增区间为_________________________.
解析:(1)由图像可以看出f(x)的单调递减区间是[-1,1].
(2)x≥0时,f(x)=x2-2x,对称轴为x=1,开口向上,在(1,+∞)单调递增,x<0时f(x)=-x2-2x,对称轴x=-1,开口向下,在(-∞,-1)单调递增,所以函数的单调递增区间是(-∞,-1)和(1,+∞).
[-1,1]
(-∞,-1)和(1,+∞)
典例剖析
用定义证明函数的单调性
思路探究:函数解析式和区间已给出,要证明函数的单调性,只需用定义证明即可。
归纳提升:利用定义证明函数单调性的步骤如下:
(1)取值:设x1、x2是该区间内的任意两个值,且x1(2)作差变形:作差f(x1)-f(x2),并通过因式分解、通分、配方、有理化等手段,转化为易判断正负的式子。
(3)定号:确定f(x1)-f(x2)的符号。
(4)结论:根据f(x1)-f(x2)的符号及定义判断单调性。
对点训练
典例剖析
证明含参数的函数的单调性
归纳提升:判断含参数的函数的单调性时,利用定义边证明边讨论,从而确定单调性。
对点训练
∴当a>0时,f(x2)-f(x1)<0,
故此时函数f(x)在(0,+∞)上是减函数,
当a<0时,f(x2)-f(x1)>0,
故此时函数f(x)在(0,+∞)上是增函数。
综上所述,当a>0时, f(x)在(0,+∞)上是减函数,
当a<0时, f(x)在(0,+∞)上是增函数。
典例剖析
函数单调性的简单应用
1.利用单调性解函数不等式
已知f(t)是定义在区间[-1,1]上的增函数,且f(x-2)<f(1-x),则x的取值范围为________.
思路探究:
典例剖析
利用函数的单调性求参数的取值范围
(0,3]
解析:因为函数f(x)在R上是增函数,所以f(x)在(-∞,1)上单调递增,故a>0,设y=ax-1,x∈(-∞,1),因为a>0,所以y<a-1.而当x≥1时,f(x)=x2+1单调递增,且此时f(x)min=12+1=2,故只需a-1≤2,即a≤3即可.所以a的取值范围是(0,3].
归纳提升:1.利用函数的单调性比较大小或解不等式
利用函数的单调性可以比较函数值或自变量的大小。
在解决比较函数值大小的问题时,要注意将对应的自变量转化到同一个单调区间上。
利用函数的单调性比较大小、解不等式时有如下结论:一是正向应用,即若y=f(x)在给定区间M上单调递增,则x1<x2且x1,x2∈M时,f(x1)<f(x2);当x1>x2且x1,x2∈M时,f(x1)>f(x2)。
二是逆向应用,即若y=f(x)在给定区间M上单调递增且x1,x2∈M,则当f(x1)<f(x2)时,x1<x2;当f(x1)>f(x2)时,x1>x2.(若y=f(x)在给定区间M上单调递减,同理可得相应结论)。
2.分段函数的单调性
解决分段函数的单调性问题时,一般从两个方面考虑:一方面每个分段区间上函数具有相同的单调性,由此列出相关式子;另一方面要考虑端点处的衔接情况,由此列出另一相关式子,求解即可。
对点训练
D
完成课后相关练习
谢谢观看
谢谢观看
第三章 函数
3.1 函数的概念与性质
3.1.2 函数的单调性
第1课时 单调性的定义与证明
基础知识
情境与问题
我们知道,“记忆”在我们的学习过程中扮演着非常重要的角色,因此有关记忆的规律一直都是人们研究的课题。德国心理学家艾宾浩斯曾经对记忆保持量进行了系统的实验研究,并给出了类似如图所示的记忆规律。
如果我们以 x 表示时间间隔 (单位: h),y 表示记忆保持量,则不难看出,上图中,y是x的函数,记这个函数为 y=f(x)。
这个函数反映出记忆具有什么规律 你能从中得到什么启发
情境与问题中的函数 y=f (x) 反映出记忆的如下规律:随着时间间隔x的增大,记忆保持量 y 将减小。
给定一个函数,人们有时候关心的是,函数值会随着自变量增大而怎样变化,类似的内容我们在初中曾经接触过。
如图,从正比例函数y=2x的图象可以看出,当自变量由小变大时,这个函数的函数值逐渐变大,即 y 随着 x 的增大而增大;从反比例函数 y=的图象可以看出,在(-∞,0)和(0,+∞)內,这个函数的函数值 y 都随着 x 的增大而减小。
一般地,设函数y=f(x)的定义域为 D,且ID:
如果对任意 x1,x2∈I,当x1<x2时,都有 f(x1)<f (x2),则称y=f(x)在I上是增函数 (也称在I上单调递增),如图(1)所示;
(2)如果对任意 x1,x2∈I,当x1<x2时,都有f(x1)>f(x2),则称
y=f(x)在I上是减函数 (也称在I上单调递减),如图(2)所示。
两种情况下,都称函数在I上具有单调性 (当I为区间时,称I为函数的单调区间,也可分别称为单调递增区间或单调递减区间)。
由增函数和减函数的定义可知,前面给出的例子中,y=2x在R上是增函数;y=在(-∞,0) 上是减函数,在 (0,+∞)上也是减函数。
尝试与发现
如图所示的函数 y=f(x),在[-6,-4] 上是增函数,在 [-4,-2] 上是减函数,在 [-2,1] 上是__________函数,在 [1,3] 上是__________函数,在 [3,6]上是__________函数。
增
增
减
由尝试与发现可知,从函数的图象能方便地看出函数的单调性。但一般情况下,得到函数的图象并不容易,而且手工作出的图象往往都不精确,因此我们要探讨怎样从函数的解析式来证明函数的单调性。这可以利用函数单调性的定义和不等式的证明方法。
思考1:若把增、减函数定义中的“任意x1,x2”改为“存在x1,x2”可以吗?
提示:不可以,如图:
思考2:“函数f(x)的单调增(减)区间是D”与“函数f(x)在区间D上是增(减)函数”是否相同?
提示:不相同。函数f(x)的单调增(减)区间是D,这一说法意味着除D之外,函数f(x)再无其他单调增(减)区间。
函数f(x)在区间D上是增(减)函数,则意味着区间D是函数f(x)的单调增(减)区间的子区间,即除区间D外,函数f(x)还可能有其他的单调增(减)区间。
典例精析
求证:函数 f(x)= -2x 在 R 上是减函数。
证明:任取x1,x2∈R且x1<x2,则x1-x2<0,那么f(x1)-f(x2)=(-2x1)-(-2x2)=2(x2-x1)>0,
从而 f(x1)>f(x2)。
因此,函数 f(x)=-2x 在 R上是减函数。
一般地,设函数 f(x)的定义域为 D,且x0∈D,如果对任意x∈D,都有f(x)≤f(x0),则称f(x)的最大值为 f(x0),而x0称为 f(x)的最大值点;如果对任意 x∈D,都有 f(x)≥f(x0),则称f(x)的最小值为f(x0),而x0称为 f(x)的最小值点。最大值和最小值统称为最值,最大值点和最小值点统称为最值点。
不难看出,如果函数有最值而且函数的单调性容易求出,则可利用函数的单调性求出函数的最值点和最值。
判断函数 f(x)=3x+5,x∈[-1,6] 的单调性,并求这个函数的最值。
典例精析
解:任取x1,x2∈[-1,6]且x1
因此,当-1≤x≤6 时,有
f(-1) ≤ f(x) ≤ f(6),
从而这个函数的最小值为 f(-1)=_______,最大值为 f(6)= _______。
结论也可由不等式的知识得到:因为-1 ≤ x ≤ 6,所以
-3≤3x≤18,2≤3x+5≤23,
即 f(-1) ≤ f(x) ≤ f(6),其余同上。
增
2
23
基础自测
1.函数f(x)=2在[-2,4]上的单调性为( )
A.减函数 B.增函数
C.先减后增 D.不具有单调性
解析:当x∈[-2,4]时,f(x)的值恒等于2,故函数f(x)=2在[-2,4]上不具有单调性.
D
2.对于函数y=f(x),在给定区间内有两个值x1、x2,且x1
C.可能是常数函数 D.单调性不能确定
解析:由函数单调性的定义可知,判断单调性时不能用特殊值代替任意值,故选D。
D
3.函数y=f(x)的图像如图所示,其增区间是___________.
4.函数f(x)=-x2-2x的单调递增区间是______________.
解析:f(x)=-(x+1)2+1,函数f(x)的对称轴为x=-1,故函数的递增区间为(-∞,-1].
[-3,1]
(-∞,-1]
5.若y=(2k-1)x+b是R上的减函数,则k的取值范围为_________,b的取值范围为____.
R
典例剖析
求函数的单调区间
已知x∈R,函数f(x)=x|x-2|,试画出y=f(x)的图像,并结合图像写出函数的单调区间。
思路探究:首先分类讨论,去掉绝对值号,将函数化为分段函数,然后画出图像求解即可。
归纳提升:1.作出函数的图像,利用图形的直观性能快速判断函数的单调区间,但要注意图像一定要画准确。
2.函数的单调区间是函数定义域的子集,在求解的过程中不要忽略了函数的定义域。
3.一个函数出现两个或两个以上的单调区间时,不能用“∪”连接两个单调区间,而要用“和”或“,”连接。
对点训练
(1)如图是定义在区间[-2,2]的函数y=f(x),则f(x)的单调递减区间是___________.
(2)函数f(x)=x|x|-2x的单调递增区间为_________________________.
解析:(1)由图像可以看出f(x)的单调递减区间是[-1,1].
(2)x≥0时,f(x)=x2-2x,对称轴为x=1,开口向上,在(1,+∞)单调递增,x<0时f(x)=-x2-2x,对称轴x=-1,开口向下,在(-∞,-1)单调递增,所以函数的单调递增区间是(-∞,-1)和(1,+∞).
[-1,1]
(-∞,-1)和(1,+∞)
典例剖析
用定义证明函数的单调性
思路探究:函数解析式和区间已给出,要证明函数的单调性,只需用定义证明即可。
归纳提升:利用定义证明函数单调性的步骤如下:
(1)取值:设x1、x2是该区间内的任意两个值,且x1
(3)定号:确定f(x1)-f(x2)的符号。
(4)结论:根据f(x1)-f(x2)的符号及定义判断单调性。
对点训练
典例剖析
证明含参数的函数的单调性
归纳提升:判断含参数的函数的单调性时,利用定义边证明边讨论,从而确定单调性。
对点训练
∴当a>0时,f(x2)-f(x1)<0,
故此时函数f(x)在(0,+∞)上是减函数,
当a<0时,f(x2)-f(x1)>0,
故此时函数f(x)在(0,+∞)上是增函数。
综上所述,当a>0时, f(x)在(0,+∞)上是减函数,
当a<0时, f(x)在(0,+∞)上是增函数。
典例剖析
函数单调性的简单应用
1.利用单调性解函数不等式
已知f(t)是定义在区间[-1,1]上的增函数,且f(x-2)<f(1-x),则x的取值范围为________.
思路探究:
典例剖析
利用函数的单调性求参数的取值范围
(0,3]
解析:因为函数f(x)在R上是增函数,所以f(x)在(-∞,1)上单调递增,故a>0,设y=ax-1,x∈(-∞,1),因为a>0,所以y<a-1.而当x≥1时,f(x)=x2+1单调递增,且此时f(x)min=12+1=2,故只需a-1≤2,即a≤3即可.所以a的取值范围是(0,3].
归纳提升:1.利用函数的单调性比较大小或解不等式
利用函数的单调性可以比较函数值或自变量的大小。
在解决比较函数值大小的问题时,要注意将对应的自变量转化到同一个单调区间上。
利用函数的单调性比较大小、解不等式时有如下结论:一是正向应用,即若y=f(x)在给定区间M上单调递增,则x1<x2且x1,x2∈M时,f(x1)<f(x2);当x1>x2且x1,x2∈M时,f(x1)>f(x2)。
二是逆向应用,即若y=f(x)在给定区间M上单调递增且x1,x2∈M,则当f(x1)<f(x2)时,x1<x2;当f(x1)>f(x2)时,x1>x2.(若y=f(x)在给定区间M上单调递减,同理可得相应结论)。
2.分段函数的单调性
解决分段函数的单调性问题时,一般从两个方面考虑:一方面每个分段区间上函数具有相同的单调性,由此列出相关式子;另一方面要考虑端点处的衔接情况,由此列出另一相关式子,求解即可。
对点训练
D
完成课后相关练习
谢谢观看
谢谢观看
