3.1.3 第1课时 函数的奇偶性 课件(共53张PPT)
文档属性
| 名称 | 3.1.3 第1课时 函数的奇偶性 课件(共53张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 706.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-25 00:00:00 | ||
图片预览










文档简介
(共53张PPT)
第三章 函数
3.1 函数的概念与性质
3.1.3 函数的奇偶性
第1课时 函数的奇偶性
基础知识
初中时我们学习过有关轴对称和中心对称的知识,而且已经知道,在平面直角坐标系中,点 (x,y) 关于 y 轴的对称点为 (-x,y),关于原点的对称点为 (-x,-y)。例如,(-2,3) 关于 y 轴的对称点为_____________,关于原点的对称点为____________.
(2,3)
(2,-3)
不难发现,上述两个函数,当自变量取互为相反数的两个值x和-x时,对应的函数值相等,即
f(-x)=(-x)2=x2 = f(x),
g(-x) = = = g(x)
一般地,设函数 y=f(x)的定义域为D,如果对D内的任意一个x,都有-x∈D,且
f(-x)=f(x),
则称 y=f(x)为偶函数
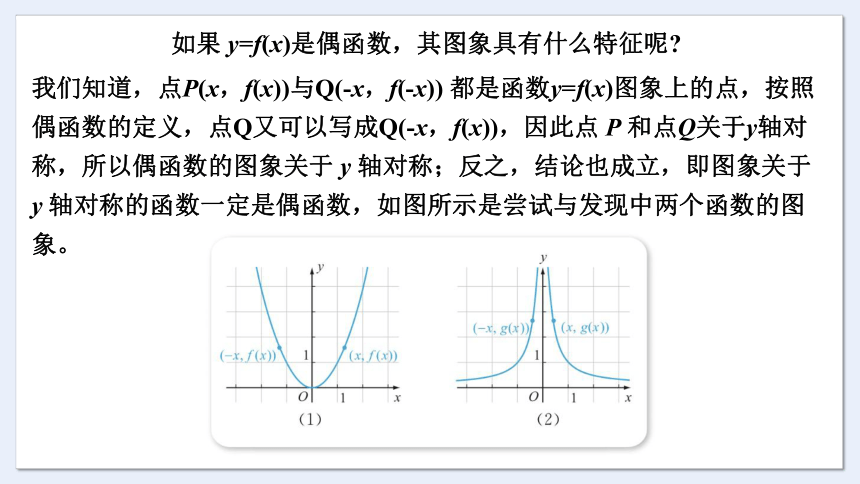
如果 y=f(x)是偶函数,其图象具有什么特征呢
我们知道,点P(x,f(x))与Q(-x,f(-x)) 都是函数y=f(x)图象上的点,按照偶函数的定义,点Q又可以写成Q(-x,f(x)),因此点 P 和点Q关于y轴对称,所以偶函数的图象关于 y 轴对称;反之,结论也成立,即图象关于 y 轴对称的函数一定是偶函数,如图所示是尝试与发现中两个函数的图象。
尝试与发现
按照类似的方式得到奇函数的定义,以及奇函数图象的特征:一般地,设函数 y=f(x) 的定义域为 D,如果对D内的任意一个x,都有__________,且
_____________
则称 y=f(x)为奇函数。
奇函数的图象关于__________对称.
-x∈D
f(-x)=- f(x)
原点
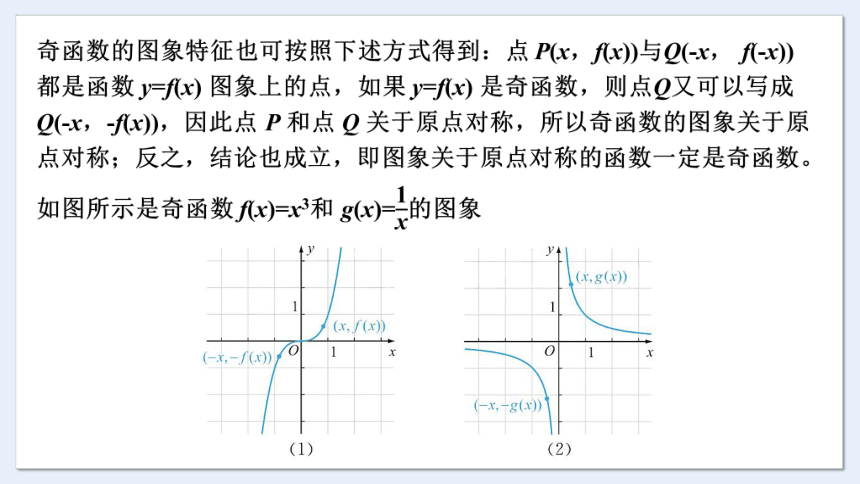
奇函数的图象特征也可按照下述方式得到:点 P(x,f(x))与Q(-x, f(-x)) 都是函数 y=f(x) 图象上的点,如果 y=f(x) 是奇函数,则点Q又可以写成 Q(-x,-f(x)),因此点 P 和点 Q 关于原点对称,所以奇函数的图象关于原点对称;反之,结论也成立,即图象关于原点对称的函数一定是奇函数。如图所示是奇函数 f(x)=x3和 g(x)=的图象
如果一个函数是偶函数或是奇函数,则称这个函数具有奇偶性。可以看出,当 n 是正整数时,函数 f(x)=x2n是偶函数,函数 g(x)= x2n-1 是奇函数。
前提 函数f(x)定义域D内的________________________,
条件 且_______________ 且_________________
结论 则称y=f(x)为偶函数 则y=f(x)为奇函数
任意一个x,都有-x∈D
f(-x)=f(x)
f(-x)=-f(x)
思考:函数奇偶性的注意点是什么?
提示:(1)从奇函数、偶函数的定义可知,当x是定义域中的一个数值时,则-x也必是定义域中的一个数值,因此函数y=f(x)是奇函数或偶函数的一个必不可少的条件是定义域关于原点对称.换言之,若所给函数的定义域不关于原点对称,则这个函数不具有奇偶性.例如,函数y=x2在区间(-∞,+∞)上是偶函数,但在区间[-3,5]上却不具有奇偶性。
(2)若奇函数f(x)在x=0处有定义,则根据定义可得,f(-0)=-f(0),即f(0)=0.
(3)若f(-x)=-f(x),且f(-x)=f(x),则f(x)既是奇函数又是偶函数,这样的函数有且只有一类,即f(x)=0,x∈D,D是关于原点对称的非空数集。
奇、偶函数的单调性
根据奇、偶函数的图像特征,我们不难得出以下结论。
(1)奇函数在关于原点对称的区间上有相同的单调性,偶函数在关于原点对称的区间上有相反的单调性.上述结论可简记为“___________”.
(2)________________________________________________,取最值时的自变量互为相反数;
___________________________________________________,取最值时的自变量也互为相反数。
奇同偶异
偶函数在关于原点对称的区间上有相同的最大(小)值
奇函数在关于原点对称的区间上的最值互为相反数
典例精析
判断下列函数是否具有奇偶性:
(1)f(x)=x+x3+x5; (2) f(x)=x2+1;
(3)f(x)=x+1; (4)f(x)=x2,x∈[-1,3].
解:(1)因为函数的定义域为 R,所以x∈R时,-x∈R。
又因为
f(-x)=(-x)+(-x)3+(-x)5= -(x+x3+x5)= -f(x),
所以函数f(x)= x+x3+x5是_________函数。
(2) 因为函数的定义域为 R,所以x∈R时,-x∈R.
又因为 f(-x)=(-x)2+1=x2+1=f(x),
所以函数f(x)=x2+1是_________函数。
奇
偶
(3)因为函数的定义域为 R,所以x∈R 时,-x∈R.
又因为 f(-1)=0,f(1)=2,所以
f(-1) ≠ -f(1)且f(-1) ≠ f(1),
因此函数 f(x)= x+1 既不是奇函数也不是偶函数(也可说成 f(x)是非奇非偶函数)。
(4)因为函数的定义域为 [-1,3],而3∈[-1,3],但-3 [-1,3],所以函数 f(x)=x2,x∈[-1,3] 是非奇非偶函数。
上题(4)说明,设函数 f(x)的定义域为 D,如果存在x0∈D,但-x0 D,即函数 f(x) 的定义域不关于原点对称,则 f(x) 既不是奇函数也不是偶函数。
已知奇函数f(x)的定义域为 D,且0∈D,求证:f(0)=0.
证明:因为 f(x) 是奇函数,所以
f(-0)= -f(0),
即f(0)= -f(0),所以 2f(0)=0,因此f(0)=0.
基础自测
D
2.对于定义域是R的任意奇函数f(x),都有( )
A.f(x)-f(-x)>0 B.f(x)-f(-x)≤0
C.f(x)·f(-x)≤0 D.f(x)·f(-x)>0
解析:∵f(x)为奇函数,∴f(-x)=-f(x).
∴f(x)·f(-x)=f(x)·[-f(x)]=-[f(x)]2≤0.
C
3.若函数f(x)=x2-ax+1为偶函数,则a=____.
解析:解法一:∵f(x)为偶函数,
∴f(-x)=f(x),
x2+ax+1=x2-ax+1,
即2ax=0(x∈R)恒成立,
∴a=0.
解法二:∵f(x)为偶函数,
∴f(-1)=f(1),即1+a+1=1-a+1,
∴a=0.
0
4.下列图像表示的函数是奇函数的是_______,是偶函数的是_______(填序号)。
解析:①③关于y轴对称是偶函数,②④关于原点对称是奇函数。
②④
①③
5.已知y=f(x)是定义在R上的奇函数,当x≥0时,f(x)=x2-2x,则f(x)在R上的解析式为_______________________.
典例剖析
判断函数的奇偶性
判断下列函数的奇偶性:
思路探究:先求定义域,验证定义域是否关于原点对称,再看f(-x)与f(x)的关系,进而做出判断。
归纳提升:如何判断函数的奇偶性
1.判断函数的奇偶性一般不用其定义,而是利用定义的等价形式,即考察f(-x)与f(x)的关系,具体步骤如下:
(1)求f(x)的定义域。
(2)若定义域不关于原点对称,则函数f(x)不具有奇偶性,若定义域关于原点对称,可再利用定义验证f(-x)与f(x)的关系。
2.关于一些较复杂的函数,也可以用如下性质判断函数的奇偶性:
(1)偶函数的和、差、积、商(分母不为零)仍为偶函数。
(2)奇函数的和、差仍为奇函数。
(3)奇(偶)数个奇函数的积、商(分母不为零)为奇(偶)函数。
(4)一个奇函数与一个偶函数的积为奇函数。
对点训练
典例剖析
奇偶函数图像的应用
(1)如图1,给出了奇函数f(x)的局部图像,那么f(1)等于 ( )
A.-4
B.-2
C.2
D.4
B
(2)设偶函数f(x)的定义域为[-5,5],且f(3)=0,当x∈[0,5]时,f(x)的图像如图2所示,则不等式xf(x)<0的解集是________________________.
思路探究:根据函数的奇偶性可作出函数在y轴另一侧的图像,再根据图像来解题。
[-5,-3)∪(0,3)
图2
归纳提升:巧用奇偶性作函数图像的步骤
(1)确定函数的奇偶性。
(2)作出函数在[0,+∞)(或(-∞,0])上对应的图像。
(3)根据奇(偶)函数关于原点(y轴)对称得出在(-∞,0]或[0,+∞)上对应的函数图像。
对点训练
已知函数y=f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x,现已画出函数f(x)在y轴左侧的图像,如图所示。
(1)请补出完整函数y=f(x)的图像;
(2)根据图像写出函数y=f(x)的增区间、值域.
解析:(1)由题意作出函数图像如图:
(2)据图可知,单调增区间为(-1,0),(1,+∞),值域为[-1,+∞)。
典例剖析
分段函数奇偶性的判定
思路探究:判断分段函数的奇偶性,要注意x与-x是在不同的“段”中,则f(-x)与f(x)是不同的关系式。
归纳提升:1.判断分段函数的奇偶性,必须分段考虑。
2.若分段函数是奇函数或偶函数,常用含绝对值符号的函数表达式来表示。
对点训练
解析:函数f(x)的定义域为R,关于原点对称,
当x>0时,-x<0,f(-x)=-(-x)2-2=-x2-2=-(x2+2)=-f(x),
当x<0时,-x>0,f(-x)=(-x)2+2=x2+2=-(-x2-2)=-f(x)。
当x=0时,f(0)=0,即x=0时,f(-x)=-f(x)。
综上所述,x∈R,有f(-x)=-f(x),故该函数为奇函数。
典例剖析
已知f(x)是奇函数,且当x>0时,f(x)=x|x-2|,求当x<0时,f(x)的表达式。
思路探究:已知函数f(x)是奇函数,可利用对称性求对称区间上的解析式。
由函数的奇偶性求函数的解析式
解析:令x<0,则-x>0.
∴f(-x)=-x|-x-2|=-x|x+2|.
∵f(x)为奇函数,∴f(-x)=-f(x).
∴f(x)=x|x+2|.
故当x<0时,f(x)的表达式为f(x)=x|x+2|.
归纳提升:由函数奇偶性求函数解析式的解题策略
1.函数具有奇偶性,若只给出了部分区间上的解析式,则可以利用函数的奇偶性求出对称区间上的解析式,其解题理论为函数奇偶性的定义。
正用定义可以判断函数的奇偶性,逆用可以求出函数在对称区间上的解析式。
2.结论:
(1)若f(x)是奇函数,且已知x>0时的解析式,则x<0时的解析式只需将原函数式y=f(x)中的x,y分别替换为-x,-y,然后解出y即可。
(2)若f(x)是偶函数,且已知x>0时的解析式,则x<0时的解析式只需将原函数式y=f(x)中的x替换为-x,y不变,即得x<0时的解析式。
对点训练
若f(x)是定义在R上的奇函数,当x<0时,f(x)=x(1-x),求:当x≥0时,函数f(x)的解析式。
解析:当x>0时,-x<0,∵当x<0时,f(x)=x(1-x),
∴f(-x)=-x(1+x),又f(x)为奇函数,∴f(-x)=-f(x),
∴-f(x)=-x(1+x),∴f(x)=x(1+x),
又f(0)=f(-0)=-f(0),∴f(0)=0,
∴当x≥0时,f(x)=x(1+x).
典例剖析
抽象函数的奇偶性
已知函数y=f(x)(x∈R),若对于任意实数a、b都有f(a+b)=f(a)+f(b),求证: f(x)为奇函数。
思路探究:因为对于任意实数a、b都有f(a+b)=f(a)+f(b),可以先令a、b为某些特殊值,从而得出f(-x)=-f(x)。
证明:令a=0,则f(b)=f(0)+f(b),
∴f(0)=0,再令a=-x,b=x,
则f(0)=f(-x)+f(x),∴f(-x)=-f(x),且定义域x∈R关于原点对称,∴f(x)是奇函数.
归纳提升:判断抽象函数的奇偶性,应利用函数奇偶性定义,找准方向,巧妙赋值,合理,灵活变形配凑,找出f(-x)与f(x)的关系,从而判断或证明抽象函数的奇偶性。
对点训练
已知函数y=f(x)(x∈R),若对于任意实数x1、x2,都有f(x1+x2)+f(x1-x2)=2f(x1)·f(x2),求证: f(x)为偶函数.
证明:令x1=0,x2=x,
得f(x)+f(-x)=2f(0)·f(x),①
令x1=x,x2=0,得f(x)+f(x)=2f(0)·f(x),②
由①②得, f(-x)=f(x),且定义域x∈R关于原点对称,
∴函数f(x)为偶函数。
完成课后相关练习
谢谢观看
谢谢观看
第三章 函数
3.1 函数的概念与性质
3.1.3 函数的奇偶性
第1课时 函数的奇偶性
基础知识
初中时我们学习过有关轴对称和中心对称的知识,而且已经知道,在平面直角坐标系中,点 (x,y) 关于 y 轴的对称点为 (-x,y),关于原点的对称点为 (-x,-y)。例如,(-2,3) 关于 y 轴的对称点为_____________,关于原点的对称点为____________.
(2,3)
(2,-3)
不难发现,上述两个函数,当自变量取互为相反数的两个值x和-x时,对应的函数值相等,即
f(-x)=(-x)2=x2 = f(x),
g(-x) = = = g(x)
一般地,设函数 y=f(x)的定义域为D,如果对D内的任意一个x,都有-x∈D,且
f(-x)=f(x),
则称 y=f(x)为偶函数
如果 y=f(x)是偶函数,其图象具有什么特征呢
我们知道,点P(x,f(x))与Q(-x,f(-x)) 都是函数y=f(x)图象上的点,按照偶函数的定义,点Q又可以写成Q(-x,f(x)),因此点 P 和点Q关于y轴对称,所以偶函数的图象关于 y 轴对称;反之,结论也成立,即图象关于 y 轴对称的函数一定是偶函数,如图所示是尝试与发现中两个函数的图象。
尝试与发现
按照类似的方式得到奇函数的定义,以及奇函数图象的特征:一般地,设函数 y=f(x) 的定义域为 D,如果对D内的任意一个x,都有__________,且
_____________
则称 y=f(x)为奇函数。
奇函数的图象关于__________对称.
-x∈D
f(-x)=- f(x)
原点
奇函数的图象特征也可按照下述方式得到:点 P(x,f(x))与Q(-x, f(-x)) 都是函数 y=f(x) 图象上的点,如果 y=f(x) 是奇函数,则点Q又可以写成 Q(-x,-f(x)),因此点 P 和点 Q 关于原点对称,所以奇函数的图象关于原点对称;反之,结论也成立,即图象关于原点对称的函数一定是奇函数。如图所示是奇函数 f(x)=x3和 g(x)=的图象
如果一个函数是偶函数或是奇函数,则称这个函数具有奇偶性。可以看出,当 n 是正整数时,函数 f(x)=x2n是偶函数,函数 g(x)= x2n-1 是奇函数。
前提 函数f(x)定义域D内的________________________,
条件 且_______________ 且_________________
结论 则称y=f(x)为偶函数 则y=f(x)为奇函数
任意一个x,都有-x∈D
f(-x)=f(x)
f(-x)=-f(x)
思考:函数奇偶性的注意点是什么?
提示:(1)从奇函数、偶函数的定义可知,当x是定义域中的一个数值时,则-x也必是定义域中的一个数值,因此函数y=f(x)是奇函数或偶函数的一个必不可少的条件是定义域关于原点对称.换言之,若所给函数的定义域不关于原点对称,则这个函数不具有奇偶性.例如,函数y=x2在区间(-∞,+∞)上是偶函数,但在区间[-3,5]上却不具有奇偶性。
(2)若奇函数f(x)在x=0处有定义,则根据定义可得,f(-0)=-f(0),即f(0)=0.
(3)若f(-x)=-f(x),且f(-x)=f(x),则f(x)既是奇函数又是偶函数,这样的函数有且只有一类,即f(x)=0,x∈D,D是关于原点对称的非空数集。
奇、偶函数的单调性
根据奇、偶函数的图像特征,我们不难得出以下结论。
(1)奇函数在关于原点对称的区间上有相同的单调性,偶函数在关于原点对称的区间上有相反的单调性.上述结论可简记为“___________”.
(2)________________________________________________,取最值时的自变量互为相反数;
___________________________________________________,取最值时的自变量也互为相反数。
奇同偶异
偶函数在关于原点对称的区间上有相同的最大(小)值
奇函数在关于原点对称的区间上的最值互为相反数
典例精析
判断下列函数是否具有奇偶性:
(1)f(x)=x+x3+x5; (2) f(x)=x2+1;
(3)f(x)=x+1; (4)f(x)=x2,x∈[-1,3].
解:(1)因为函数的定义域为 R,所以x∈R时,-x∈R。
又因为
f(-x)=(-x)+(-x)3+(-x)5= -(x+x3+x5)= -f(x),
所以函数f(x)= x+x3+x5是_________函数。
(2) 因为函数的定义域为 R,所以x∈R时,-x∈R.
又因为 f(-x)=(-x)2+1=x2+1=f(x),
所以函数f(x)=x2+1是_________函数。
奇
偶
(3)因为函数的定义域为 R,所以x∈R 时,-x∈R.
又因为 f(-1)=0,f(1)=2,所以
f(-1) ≠ -f(1)且f(-1) ≠ f(1),
因此函数 f(x)= x+1 既不是奇函数也不是偶函数(也可说成 f(x)是非奇非偶函数)。
(4)因为函数的定义域为 [-1,3],而3∈[-1,3],但-3 [-1,3],所以函数 f(x)=x2,x∈[-1,3] 是非奇非偶函数。
上题(4)说明,设函数 f(x)的定义域为 D,如果存在x0∈D,但-x0 D,即函数 f(x) 的定义域不关于原点对称,则 f(x) 既不是奇函数也不是偶函数。
已知奇函数f(x)的定义域为 D,且0∈D,求证:f(0)=0.
证明:因为 f(x) 是奇函数,所以
f(-0)= -f(0),
即f(0)= -f(0),所以 2f(0)=0,因此f(0)=0.
基础自测
D
2.对于定义域是R的任意奇函数f(x),都有( )
A.f(x)-f(-x)>0 B.f(x)-f(-x)≤0
C.f(x)·f(-x)≤0 D.f(x)·f(-x)>0
解析:∵f(x)为奇函数,∴f(-x)=-f(x).
∴f(x)·f(-x)=f(x)·[-f(x)]=-[f(x)]2≤0.
C
3.若函数f(x)=x2-ax+1为偶函数,则a=____.
解析:解法一:∵f(x)为偶函数,
∴f(-x)=f(x),
x2+ax+1=x2-ax+1,
即2ax=0(x∈R)恒成立,
∴a=0.
解法二:∵f(x)为偶函数,
∴f(-1)=f(1),即1+a+1=1-a+1,
∴a=0.
0
4.下列图像表示的函数是奇函数的是_______,是偶函数的是_______(填序号)。
解析:①③关于y轴对称是偶函数,②④关于原点对称是奇函数。
②④
①③
5.已知y=f(x)是定义在R上的奇函数,当x≥0时,f(x)=x2-2x,则f(x)在R上的解析式为_______________________.
典例剖析
判断函数的奇偶性
判断下列函数的奇偶性:
思路探究:先求定义域,验证定义域是否关于原点对称,再看f(-x)与f(x)的关系,进而做出判断。
归纳提升:如何判断函数的奇偶性
1.判断函数的奇偶性一般不用其定义,而是利用定义的等价形式,即考察f(-x)与f(x)的关系,具体步骤如下:
(1)求f(x)的定义域。
(2)若定义域不关于原点对称,则函数f(x)不具有奇偶性,若定义域关于原点对称,可再利用定义验证f(-x)与f(x)的关系。
2.关于一些较复杂的函数,也可以用如下性质判断函数的奇偶性:
(1)偶函数的和、差、积、商(分母不为零)仍为偶函数。
(2)奇函数的和、差仍为奇函数。
(3)奇(偶)数个奇函数的积、商(分母不为零)为奇(偶)函数。
(4)一个奇函数与一个偶函数的积为奇函数。
对点训练
典例剖析
奇偶函数图像的应用
(1)如图1,给出了奇函数f(x)的局部图像,那么f(1)等于 ( )
A.-4
B.-2
C.2
D.4
B
(2)设偶函数f(x)的定义域为[-5,5],且f(3)=0,当x∈[0,5]时,f(x)的图像如图2所示,则不等式xf(x)<0的解集是________________________.
思路探究:根据函数的奇偶性可作出函数在y轴另一侧的图像,再根据图像来解题。
[-5,-3)∪(0,3)
图2
归纳提升:巧用奇偶性作函数图像的步骤
(1)确定函数的奇偶性。
(2)作出函数在[0,+∞)(或(-∞,0])上对应的图像。
(3)根据奇(偶)函数关于原点(y轴)对称得出在(-∞,0]或[0,+∞)上对应的函数图像。
对点训练
已知函数y=f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x,现已画出函数f(x)在y轴左侧的图像,如图所示。
(1)请补出完整函数y=f(x)的图像;
(2)根据图像写出函数y=f(x)的增区间、值域.
解析:(1)由题意作出函数图像如图:
(2)据图可知,单调增区间为(-1,0),(1,+∞),值域为[-1,+∞)。
典例剖析
分段函数奇偶性的判定
思路探究:判断分段函数的奇偶性,要注意x与-x是在不同的“段”中,则f(-x)与f(x)是不同的关系式。
归纳提升:1.判断分段函数的奇偶性,必须分段考虑。
2.若分段函数是奇函数或偶函数,常用含绝对值符号的函数表达式来表示。
对点训练
解析:函数f(x)的定义域为R,关于原点对称,
当x>0时,-x<0,f(-x)=-(-x)2-2=-x2-2=-(x2+2)=-f(x),
当x<0时,-x>0,f(-x)=(-x)2+2=x2+2=-(-x2-2)=-f(x)。
当x=0时,f(0)=0,即x=0时,f(-x)=-f(x)。
综上所述,x∈R,有f(-x)=-f(x),故该函数为奇函数。
典例剖析
已知f(x)是奇函数,且当x>0时,f(x)=x|x-2|,求当x<0时,f(x)的表达式。
思路探究:已知函数f(x)是奇函数,可利用对称性求对称区间上的解析式。
由函数的奇偶性求函数的解析式
解析:令x<0,则-x>0.
∴f(-x)=-x|-x-2|=-x|x+2|.
∵f(x)为奇函数,∴f(-x)=-f(x).
∴f(x)=x|x+2|.
故当x<0时,f(x)的表达式为f(x)=x|x+2|.
归纳提升:由函数奇偶性求函数解析式的解题策略
1.函数具有奇偶性,若只给出了部分区间上的解析式,则可以利用函数的奇偶性求出对称区间上的解析式,其解题理论为函数奇偶性的定义。
正用定义可以判断函数的奇偶性,逆用可以求出函数在对称区间上的解析式。
2.结论:
(1)若f(x)是奇函数,且已知x>0时的解析式,则x<0时的解析式只需将原函数式y=f(x)中的x,y分别替换为-x,-y,然后解出y即可。
(2)若f(x)是偶函数,且已知x>0时的解析式,则x<0时的解析式只需将原函数式y=f(x)中的x替换为-x,y不变,即得x<0时的解析式。
对点训练
若f(x)是定义在R上的奇函数,当x<0时,f(x)=x(1-x),求:当x≥0时,函数f(x)的解析式。
解析:当x>0时,-x<0,∵当x<0时,f(x)=x(1-x),
∴f(-x)=-x(1+x),又f(x)为奇函数,∴f(-x)=-f(x),
∴-f(x)=-x(1+x),∴f(x)=x(1+x),
又f(0)=f(-0)=-f(0),∴f(0)=0,
∴当x≥0时,f(x)=x(1+x).
典例剖析
抽象函数的奇偶性
已知函数y=f(x)(x∈R),若对于任意实数a、b都有f(a+b)=f(a)+f(b),求证: f(x)为奇函数。
思路探究:因为对于任意实数a、b都有f(a+b)=f(a)+f(b),可以先令a、b为某些特殊值,从而得出f(-x)=-f(x)。
证明:令a=0,则f(b)=f(0)+f(b),
∴f(0)=0,再令a=-x,b=x,
则f(0)=f(-x)+f(x),∴f(-x)=-f(x),且定义域x∈R关于原点对称,∴f(x)是奇函数.
归纳提升:判断抽象函数的奇偶性,应利用函数奇偶性定义,找准方向,巧妙赋值,合理,灵活变形配凑,找出f(-x)与f(x)的关系,从而判断或证明抽象函数的奇偶性。
对点训练
已知函数y=f(x)(x∈R),若对于任意实数x1、x2,都有f(x1+x2)+f(x1-x2)=2f(x1)·f(x2),求证: f(x)为偶函数.
证明:令x1=0,x2=x,
得f(x)+f(-x)=2f(0)·f(x),①
令x1=x,x2=0,得f(x)+f(x)=2f(0)·f(x),②
由①②得, f(-x)=f(x),且定义域x∈R关于原点对称,
∴函数f(x)为偶函数。
完成课后相关练习
谢谢观看
谢谢观看
