3.1.3 第2课时 函数奇偶性的应用 课件(共42张PPT)
文档属性
| 名称 | 3.1.3 第2课时 函数奇偶性的应用 课件(共42张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 610.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-25 18:58:33 | ||
图片预览











文档简介
(共42张PPT)
第三章 函数
3.1 函数的概念与性质
3.1.3 函数的奇偶性
第2课时 函数奇偶性的应用
基础知识
因为函数的奇偶性描述了函数图象具有的对称性,所以利用函数的奇偶性能简化函数性质的研究。如果知道一个函数是奇函数或是偶函数,那么其定义域能分成关于原点对称的两部分,得出函数在其中一部分上的性质和图象,就可得出这个函数在另一部分上的性质和图象。
尝试与发现
已知函数 f(x) 满足 f(5)= -3,分别在条件“f(x)是偶函数”与“f(x)是奇函数”下求出 f(-5) 的值。
显然,如果 f(x)是偶函数,则 f(-5)= f(5)= -3;如果 f(x)是奇函数,则f(-5)= -f(5) =3.
典例精析
已知函数 f(x) 满足 f(5)<f(3),分别在下列各条件下比较f(-5)与f(-3)的大小:
(1) f(x)是函数; (2) f(x)是函数
解:(1) 因为 f(x) 是偶函数,所以 f(-x)= f(x) ,因此
f(-5)= f(5) , f(-3)= f(3),
从而由条件可知 f(-5)(2) 因为 f(x) 是函数,所以 f(-x)= -f(x) ,因此
f(-5)= -f(5) , f(-3)= -f(3),
又由条件可知-f(5)>-f(3),从而 f(-5)>f(-3).
说明,当f(x)具有奇偶性时,函数的单调性会有一定规律。
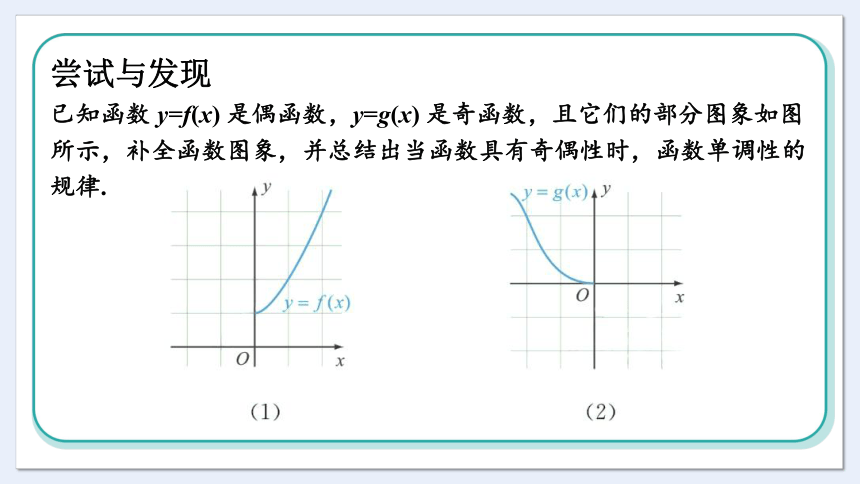
尝试与发现
已知函数 y=f(x) 是偶函数,y=g(x) 是奇函数,且它们的部分图象如图所示,补全函数图象,并总结出当函数具有奇偶性时,函数单调性的规律.
不难看出,如果 y=f(x)是偶函数,那么其在x>0与x<0 时的单调性相反;如果 y=f(x)是奇函数,那么其在x>0 与x<0时的单调性相同。
典例精析
研究函数 y=的性质,并作出函数图象
解:要使函数表达式有意义,需有x≠0,因此函数的定义域为
D={x∈R|x≠0},
从而可知函数的图象有左右两部分.
设f(x)=,则对任意x∈D,都有-x∈D,而且
f(-x)= = = f(x)
所以函数 y=是偶函数,函数的两部分图象关于 y 轴对称。
下面研究函数在区间 (0,+∞) 上的性质及图象.
因为x1,x2∈(0,+∞) 时,有
所以 y=在(0,+∞)上是减函数
又因为x∈(0,+∞)时, y=>0,所以函数图象在右边的部分一定在第一象限。列出部分函数值如下表所示,然后可以描点作图。
再根据函数是偶函数,可以得出函数的图象,如图所示,而且函数的定义域为{x∈R| x≠0},函数是偶函数,在 (-∞,0)上单调递增,在(0,+∞)上单调递减,函数的值域是(0,+∞)。
利用研究奇偶函数的类似方法还可以研究更一般的函数图象的对称性。
尝试与发现
初中时,我们就在观察图象的基础上总结出过这个结论,但当时并没有给出严格的证明。为了证明函数的图象关于x=0(即 y 轴) 对称,只需证明x轴上关于原点对称的两点对应的函数值相等,那么该怎样证明函数的图象关于x= -2 对称呢
如图所示,已知数轴上的 A,B 两点关于-2对应的点对称,而且点A的坐标是-2+h,则点 B 的坐标是______________
-2-h
证明:任取h∈R,因为
f(-2+h)=(-2+h)2+4(-2+h)+6
=h2+2,
f(-2-h)=(-2-h)2+4(-2-h)+6
=h2+2,
所以 f(-2+h)=f(-2-h),这就说明函数的图象关于 x= -2 对称。
求证:二次函数 f(x)= x +4x+6 的图象关于 x = -2 对称.
典例精析
由上题可知,要证明函数图象关于垂直于 x 轴的直线对称并不难,但怎样才能找到对应的对称轴呢?以上题所示的二次函数为例,注意到
f(x)=x2+4x+6=(x+2)2+2,
由此就容易得到 f(-2+h)=f(-2-h),从而可知 f(x)图象的对称轴为x=-2.
定义
(2)_______法:奇(偶)函数的充要条件是它的图像关于原点(或y轴)对称.
(3)_______法:偶函数的和、差、积、商(分母不为零)仍为偶函数;奇函数的和、差仍为奇函数;奇(偶)数个奇函数的积、商(分母不为零)为奇(偶)函数;一个奇函数与一个偶函数的积为奇函数.
(注:利用上述结论要注意各函数的定义域)
2.F1(x)=f(x)+f(-x)为偶函数,F2(x)=f(x)-f(-x)为奇函数.(注:F1(x)、F2(x)的定义域是关于原点对称的区间)
3.奇函数在关于原点对称的两个区间上单调性相_____;偶函数在关于原点对称的两个区间上的单调性相_____.
图像
性质
同
反
基础自测
A
2.若函数f(x)=x3,则函数g(x)=f(-2x)在其定义域上是( )
A.单调递增的偶函数
B.单调递增的奇函数
C.单调递减的偶函数
D.单调递减的奇函数
解析:∵f(x)=x3,∴g(x)=f(-2x)=-8x3.又g(-x)=8x3=-g(x),∴g(x)为奇函数.又∵f(x)=x3为增函数,∴g(x)=-8x3为减函数.
D
3.已知函数f(x)是奇函数,x>0时,f(x)=1,则f(-2)=( )
A.0 B.1
C.-1 D.±1
解析:设x<0,则-x>0,f(-x)=1.
∵f(x)是奇函数,∴f(-x)=-f(x).
∴-f(x)=1,f(x)=-1(x<0).
∴f(-2)=-1.
C
4.偶函数f(x)在区间[0,+∞)上的图像如图,则函数f(x)的增区间为______________________.
解析:由图像可知当x>0时,f(x)在[0,1]上单调递减,在[1,+∞)上单调递增,又∵f(x)为偶函数,∴f(x)的图像关于y轴对称。
∴f(x)在[-1,0]上单调递增,在(-∞,-1]上单调递减。故f(x)的增区间为[-1,0]和[1,+∞)。
[-1,0]和[1,+∞)
5.若函数f(x)=x2-|x+a|为偶函数,求实数a的值。
解析:∵函数f(x)=x2-|x+a|为偶函数,
∴f(-x)=f(x),
即(-x)2-|-x+a|=x2-|x+a|,
∴|-x+a|=|x+a|,
即|x-a|=|x+a|,∴a=0.
典例剖析
利用奇偶性求函数值
(1)已知函数f(x)=ax3+bx-6,且f(-2)=8,则f(2)=_______.
(2)已知f(x),g(x)均为R上的奇函数,且F(x)=af(x)+bg(x)+2在区间(0,+∞)上的最大值为8,则在区间(-∞,0)上的最小值为______.
-20
-4
思路探究:(1)可构造g(x)=ax3+bx,利用g(x)的奇偶性求解。
(2)因为f(x)和g(x)的具体表达式并没有给出,因此应充分利用“f(x),g(x)均为R上的奇函数”这一条件,构造一个新函数来间接求解.
解析:(1)方法一 令g(x)=ax3+bx,易知g(x)是奇函数,
从而g(-2)=-g(2).
由f(x)=g(x)-6,得f(-2)=g(-2)-6=8,
∴g(-2)=14,
∴g(2)=-g(-2)=-14,
∴f(2)=g(2)-6=-14-6=-20.
(2)由f(x),g(x)均为R上的奇函数,知af(x)+bg(x)为R上的奇函数.由F(x)=af(x)+bg(x)+2在(0,+∞)上的最大值为8,得F(x)-2=af(x)+bg(x)在(0,+∞)上的最大值为6.根据奇函数的性质可知F(x)-2=af(x)+bg(x)在(-∞,0)上的最小值为-6,故F(x)=af(x)+bg(x)+2在(-∞,0)上的最小值为-6+2=-4.
归纳提升:利用函数奇偶性求函数值的解题思路
已知f(a)求f(-a)的思路:判断f(x)的奇偶性或构造已知奇偶性的函数,利用奇偶性找出f(a)与f(-a)的关系,若还有其他条件,可再利用其转化,进而求出f(-a).
对点训练
已知f(x)是奇函数,g(x)是偶函数,且f(-1)+g(1)=2,f(1)+g(-1)=4,则g(1)=____.
解析:由题意知f(-1)+g(1)=-f(1)+g(1)=2,f(1)+g(-1)=f(1)+g(1)=4,两式相加,解得g(1)=3.
3
典例精析
含有参数的函数的奇偶性的判断
设a为实数,讨论函数f(x)=x2+|x-a|+1的奇偶性.
思路探究:以a是否为0进行分类讨论.
解析:当a=0时,f(x)=x2+|x|+1,
∴f(-x)=(-x)2+|-x|+1=x2+|x|+1=f(x),
∴当a=0时,函数f(x)为偶函数.
当a≠0时,f(1)=2+|1-a|,f(-1)=2+|1+a|,
假设f(1)=f(-1),
则|1-a|=|1+a|,(1-a)2=(1+a)2,
∴a=0,这与a≠0矛盾,
假设f(-1)=-f(1),则2+|1+a|=-2-|1-a|这显然不可能成立(∵2+|1+a|>0,-2-|1-a|<0),
∴f(-1)≠f(1),f(-1)≠-f(1),
∴当a≠0时,函数f(x)是非奇非偶函数。
归纳提升:判断含参数的函数的奇偶性时,应注意对参数进行分类讨论,若函数为非奇非偶函数时,可用特值法进行判断。
对点训练
当a≠0时,f(1)=1+a,f(-1)=1-a,
∴f(-1)≠f(1),∴f(x)不是偶函数.
f(-1)+f(1)=2≠0,
∴f(-1)≠-f(1),
∴f(x)不是奇函数.
∴f(x)既不是奇函数,也不是偶函数.
典例剖析
函数奇偶性与图像的对称性的综合应用
(1)定义在R上的函数f(x)在(-∞,2)上是增函数,且f(x+2)为偶函数,则( )
A.f(-1)<f(3) B.f(0)>f(3)
C.f(-1)=f(3) D.f(0)=f(3)
A
0
归纳提升:
(1)解决函数奇偶性与图像的对称性的综合问题时,要注意把已知函数的奇偶性按定义转化,再判断函数图像的对称轴或对称中心,也可利用图像变化关系得出函数图像的对称性。总之,要充分利用已知条件进行适当转化。
(2)关于函数的对称性
函数f(x)若对于任意x∈R,a是常数,
①关于直线x=a对称: f(a+x)=f(a-x)(f(2a-x)=f(x)),
②关于点(a,b)对称: f(a+x)+f(a-x)=2b(f(2a-x)+f(x)=2b),
特别地:关于点(a,0)对称,则f(a+h)=-f(a-h).
对点训练
典例剖析
忽略题目中的隐含条件致错
已知函数f(x)=x2-2ax+b是定义在区间[-2b,3b-1]上的偶函数,则函数f(x)的值域为_________.
错因探究:此处易忽略函数的定义域关于坐标原点对称这一隐含条件。
[1,5]
解析:∵f(x)为偶函数,∴f(-x)=f(x),即a=0.
又f(x)的定义域为[-2b,3b-1],
∴-2b+3b-1=0,∴b=1.
∴f(x)=x2+1,x∈[-2,2],
∴函数f(x)的值域为[1,5].
误区警示:f(x)是奇(偶)函数,包含两个条件:①定义域关于坐标原点对称;②f(-x)=-f(x)(f(-x)=f(x)).切记不能漏掉①。
奇偶性与单调性的综合应用
1.比较大小问题,一般解法是利用奇偶性,把不在同一单调区间上的两个或多个自变量的函数值转化为与在同一单调区间上的自变量的函数值有关,然后利用单调性比较大小。
2.抽象不等式问题的解题步骤如下:
(1)将所给的不等式转化为两个函数值的大小关系;
(2)利用单调性脱去符号“f ”,转化为解不等式(组)的问题。
需要注意的是:在转化时,自变量的取值必须在同一单调区间上;当不等式一边没有符号“f ”时,需要转化为含有符号“f ”的形式,如0=f(1),f(x-1)<0,则f(x-1)<f(1);偶函数中f(x)=f(|x|)的灵活应用。
典例剖析
已知函数f(x)是定义在(-2,2)上的奇函数且是减函数,若f(m-1)+f(1-2m)≥0,求实数m的取值范围。
思路探究:利用函数的单调性、奇偶性,化“抽象的不等式”为“具体的代数不等式”。
完成课后相关练习
谢谢观看
谢谢观看
第三章 函数
3.1 函数的概念与性质
3.1.3 函数的奇偶性
第2课时 函数奇偶性的应用
基础知识
因为函数的奇偶性描述了函数图象具有的对称性,所以利用函数的奇偶性能简化函数性质的研究。如果知道一个函数是奇函数或是偶函数,那么其定义域能分成关于原点对称的两部分,得出函数在其中一部分上的性质和图象,就可得出这个函数在另一部分上的性质和图象。
尝试与发现
已知函数 f(x) 满足 f(5)= -3,分别在条件“f(x)是偶函数”与“f(x)是奇函数”下求出 f(-5) 的值。
显然,如果 f(x)是偶函数,则 f(-5)= f(5)= -3;如果 f(x)是奇函数,则f(-5)= -f(5) =3.
典例精析
已知函数 f(x) 满足 f(5)<f(3),分别在下列各条件下比较f(-5)与f(-3)的大小:
(1) f(x)是函数; (2) f(x)是函数
解:(1) 因为 f(x) 是偶函数,所以 f(-x)= f(x) ,因此
f(-5)= f(5) , f(-3)= f(3),
从而由条件可知 f(-5)
f(-5)= -f(5) , f(-3)= -f(3),
又由条件可知-f(5)>-f(3),从而 f(-5)>f(-3).
说明,当f(x)具有奇偶性时,函数的单调性会有一定规律。
尝试与发现
已知函数 y=f(x) 是偶函数,y=g(x) 是奇函数,且它们的部分图象如图所示,补全函数图象,并总结出当函数具有奇偶性时,函数单调性的规律.
不难看出,如果 y=f(x)是偶函数,那么其在x>0与x<0 时的单调性相反;如果 y=f(x)是奇函数,那么其在x>0 与x<0时的单调性相同。
典例精析
研究函数 y=的性质,并作出函数图象
解:要使函数表达式有意义,需有x≠0,因此函数的定义域为
D={x∈R|x≠0},
从而可知函数的图象有左右两部分.
设f(x)=,则对任意x∈D,都有-x∈D,而且
f(-x)= = = f(x)
所以函数 y=是偶函数,函数的两部分图象关于 y 轴对称。
下面研究函数在区间 (0,+∞) 上的性质及图象.
因为x1,x2∈(0,+∞) 时,有
所以 y=在(0,+∞)上是减函数
又因为x∈(0,+∞)时, y=>0,所以函数图象在右边的部分一定在第一象限。列出部分函数值如下表所示,然后可以描点作图。
再根据函数是偶函数,可以得出函数的图象,如图所示,而且函数的定义域为{x∈R| x≠0},函数是偶函数,在 (-∞,0)上单调递增,在(0,+∞)上单调递减,函数的值域是(0,+∞)。
利用研究奇偶函数的类似方法还可以研究更一般的函数图象的对称性。
尝试与发现
初中时,我们就在观察图象的基础上总结出过这个结论,但当时并没有给出严格的证明。为了证明函数的图象关于x=0(即 y 轴) 对称,只需证明x轴上关于原点对称的两点对应的函数值相等,那么该怎样证明函数的图象关于x= -2 对称呢
如图所示,已知数轴上的 A,B 两点关于-2对应的点对称,而且点A的坐标是-2+h,则点 B 的坐标是______________
-2-h
证明:任取h∈R,因为
f(-2+h)=(-2+h)2+4(-2+h)+6
=h2+2,
f(-2-h)=(-2-h)2+4(-2-h)+6
=h2+2,
所以 f(-2+h)=f(-2-h),这就说明函数的图象关于 x= -2 对称。
求证:二次函数 f(x)= x +4x+6 的图象关于 x = -2 对称.
典例精析
由上题可知,要证明函数图象关于垂直于 x 轴的直线对称并不难,但怎样才能找到对应的对称轴呢?以上题所示的二次函数为例,注意到
f(x)=x2+4x+6=(x+2)2+2,
由此就容易得到 f(-2+h)=f(-2-h),从而可知 f(x)图象的对称轴为x=-2.
定义
(2)_______法:奇(偶)函数的充要条件是它的图像关于原点(或y轴)对称.
(3)_______法:偶函数的和、差、积、商(分母不为零)仍为偶函数;奇函数的和、差仍为奇函数;奇(偶)数个奇函数的积、商(分母不为零)为奇(偶)函数;一个奇函数与一个偶函数的积为奇函数.
(注:利用上述结论要注意各函数的定义域)
2.F1(x)=f(x)+f(-x)为偶函数,F2(x)=f(x)-f(-x)为奇函数.(注:F1(x)、F2(x)的定义域是关于原点对称的区间)
3.奇函数在关于原点对称的两个区间上单调性相_____;偶函数在关于原点对称的两个区间上的单调性相_____.
图像
性质
同
反
基础自测
A
2.若函数f(x)=x3,则函数g(x)=f(-2x)在其定义域上是( )
A.单调递增的偶函数
B.单调递增的奇函数
C.单调递减的偶函数
D.单调递减的奇函数
解析:∵f(x)=x3,∴g(x)=f(-2x)=-8x3.又g(-x)=8x3=-g(x),∴g(x)为奇函数.又∵f(x)=x3为增函数,∴g(x)=-8x3为减函数.
D
3.已知函数f(x)是奇函数,x>0时,f(x)=1,则f(-2)=( )
A.0 B.1
C.-1 D.±1
解析:设x<0,则-x>0,f(-x)=1.
∵f(x)是奇函数,∴f(-x)=-f(x).
∴-f(x)=1,f(x)=-1(x<0).
∴f(-2)=-1.
C
4.偶函数f(x)在区间[0,+∞)上的图像如图,则函数f(x)的增区间为______________________.
解析:由图像可知当x>0时,f(x)在[0,1]上单调递减,在[1,+∞)上单调递增,又∵f(x)为偶函数,∴f(x)的图像关于y轴对称。
∴f(x)在[-1,0]上单调递增,在(-∞,-1]上单调递减。故f(x)的增区间为[-1,0]和[1,+∞)。
[-1,0]和[1,+∞)
5.若函数f(x)=x2-|x+a|为偶函数,求实数a的值。
解析:∵函数f(x)=x2-|x+a|为偶函数,
∴f(-x)=f(x),
即(-x)2-|-x+a|=x2-|x+a|,
∴|-x+a|=|x+a|,
即|x-a|=|x+a|,∴a=0.
典例剖析
利用奇偶性求函数值
(1)已知函数f(x)=ax3+bx-6,且f(-2)=8,则f(2)=_______.
(2)已知f(x),g(x)均为R上的奇函数,且F(x)=af(x)+bg(x)+2在区间(0,+∞)上的最大值为8,则在区间(-∞,0)上的最小值为______.
-20
-4
思路探究:(1)可构造g(x)=ax3+bx,利用g(x)的奇偶性求解。
(2)因为f(x)和g(x)的具体表达式并没有给出,因此应充分利用“f(x),g(x)均为R上的奇函数”这一条件,构造一个新函数来间接求解.
解析:(1)方法一 令g(x)=ax3+bx,易知g(x)是奇函数,
从而g(-2)=-g(2).
由f(x)=g(x)-6,得f(-2)=g(-2)-6=8,
∴g(-2)=14,
∴g(2)=-g(-2)=-14,
∴f(2)=g(2)-6=-14-6=-20.
(2)由f(x),g(x)均为R上的奇函数,知af(x)+bg(x)为R上的奇函数.由F(x)=af(x)+bg(x)+2在(0,+∞)上的最大值为8,得F(x)-2=af(x)+bg(x)在(0,+∞)上的最大值为6.根据奇函数的性质可知F(x)-2=af(x)+bg(x)在(-∞,0)上的最小值为-6,故F(x)=af(x)+bg(x)+2在(-∞,0)上的最小值为-6+2=-4.
归纳提升:利用函数奇偶性求函数值的解题思路
已知f(a)求f(-a)的思路:判断f(x)的奇偶性或构造已知奇偶性的函数,利用奇偶性找出f(a)与f(-a)的关系,若还有其他条件,可再利用其转化,进而求出f(-a).
对点训练
已知f(x)是奇函数,g(x)是偶函数,且f(-1)+g(1)=2,f(1)+g(-1)=4,则g(1)=____.
解析:由题意知f(-1)+g(1)=-f(1)+g(1)=2,f(1)+g(-1)=f(1)+g(1)=4,两式相加,解得g(1)=3.
3
典例精析
含有参数的函数的奇偶性的判断
设a为实数,讨论函数f(x)=x2+|x-a|+1的奇偶性.
思路探究:以a是否为0进行分类讨论.
解析:当a=0时,f(x)=x2+|x|+1,
∴f(-x)=(-x)2+|-x|+1=x2+|x|+1=f(x),
∴当a=0时,函数f(x)为偶函数.
当a≠0时,f(1)=2+|1-a|,f(-1)=2+|1+a|,
假设f(1)=f(-1),
则|1-a|=|1+a|,(1-a)2=(1+a)2,
∴a=0,这与a≠0矛盾,
假设f(-1)=-f(1),则2+|1+a|=-2-|1-a|这显然不可能成立(∵2+|1+a|>0,-2-|1-a|<0),
∴f(-1)≠f(1),f(-1)≠-f(1),
∴当a≠0时,函数f(x)是非奇非偶函数。
归纳提升:判断含参数的函数的奇偶性时,应注意对参数进行分类讨论,若函数为非奇非偶函数时,可用特值法进行判断。
对点训练
当a≠0时,f(1)=1+a,f(-1)=1-a,
∴f(-1)≠f(1),∴f(x)不是偶函数.
f(-1)+f(1)=2≠0,
∴f(-1)≠-f(1),
∴f(x)不是奇函数.
∴f(x)既不是奇函数,也不是偶函数.
典例剖析
函数奇偶性与图像的对称性的综合应用
(1)定义在R上的函数f(x)在(-∞,2)上是增函数,且f(x+2)为偶函数,则( )
A.f(-1)<f(3) B.f(0)>f(3)
C.f(-1)=f(3) D.f(0)=f(3)
A
0
归纳提升:
(1)解决函数奇偶性与图像的对称性的综合问题时,要注意把已知函数的奇偶性按定义转化,再判断函数图像的对称轴或对称中心,也可利用图像变化关系得出函数图像的对称性。总之,要充分利用已知条件进行适当转化。
(2)关于函数的对称性
函数f(x)若对于任意x∈R,a是常数,
①关于直线x=a对称: f(a+x)=f(a-x)(f(2a-x)=f(x)),
②关于点(a,b)对称: f(a+x)+f(a-x)=2b(f(2a-x)+f(x)=2b),
特别地:关于点(a,0)对称,则f(a+h)=-f(a-h).
对点训练
典例剖析
忽略题目中的隐含条件致错
已知函数f(x)=x2-2ax+b是定义在区间[-2b,3b-1]上的偶函数,则函数f(x)的值域为_________.
错因探究:此处易忽略函数的定义域关于坐标原点对称这一隐含条件。
[1,5]
解析:∵f(x)为偶函数,∴f(-x)=f(x),即a=0.
又f(x)的定义域为[-2b,3b-1],
∴-2b+3b-1=0,∴b=1.
∴f(x)=x2+1,x∈[-2,2],
∴函数f(x)的值域为[1,5].
误区警示:f(x)是奇(偶)函数,包含两个条件:①定义域关于坐标原点对称;②f(-x)=-f(x)(f(-x)=f(x)).切记不能漏掉①。
奇偶性与单调性的综合应用
1.比较大小问题,一般解法是利用奇偶性,把不在同一单调区间上的两个或多个自变量的函数值转化为与在同一单调区间上的自变量的函数值有关,然后利用单调性比较大小。
2.抽象不等式问题的解题步骤如下:
(1)将所给的不等式转化为两个函数值的大小关系;
(2)利用单调性脱去符号“f ”,转化为解不等式(组)的问题。
需要注意的是:在转化时,自变量的取值必须在同一单调区间上;当不等式一边没有符号“f ”时,需要转化为含有符号“f ”的形式,如0=f(1),f(x-1)<0,则f(x-1)<f(1);偶函数中f(x)=f(|x|)的灵活应用。
典例剖析
已知函数f(x)是定义在(-2,2)上的奇函数且是减函数,若f(m-1)+f(1-2m)≥0,求实数m的取值范围。
思路探究:利用函数的单调性、奇偶性,化“抽象的不等式”为“具体的代数不等式”。
完成课后相关练习
谢谢观看
谢谢观看
