3.3 函数的应用(一)、3.4数学建模活动:决定苹果的最佳出售时间点 课件(共63张PPT)
文档属性
| 名称 | 3.3 函数的应用(一)、3.4数学建模活动:决定苹果的最佳出售时间点 课件(共63张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 714.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-25 18:59:50 | ||
图片预览










文档简介
(共63张PPT)
第三章 函数
3.3 函数的应用(一)
3.4 数学建模活动:
决定苹果的最佳出售时间点
基础知识
常见的函数模型
(1)一次函数模型
形如y=kx+b(k≠0)的函数模型是一次函数模型。应用一次函数的性质及图像解题时,应注意:
①一次函数有单调递增(一次项系数为正)和单调递减(一次项系数为负)两种情况;
②一次函数的图像是一条直线。
(2)二次函数模型
形如y=ax2+bx+c(a≠0)的函数模型是二次函数模型。二次函数模型是重要的数学模型之一,依据实际问题建立二次函数的解析式后,利用配方法求最值简单易懂,有时也可以依据二次函数的性质求最值,从而解决利润最大、用料最省等问题。
思考:一次、二次函数模型的定义域都是全体实数,在实际应用问题中,定义域一定是全体实数吗?
提示:不一定。在实际应用中,函数的自变量x往往具有实际意义,如x表示长度时,x≥0;x表示件数时,x≥0,且x∈Z等。在解答时,必须要考虑这些实际意义。
典例精析
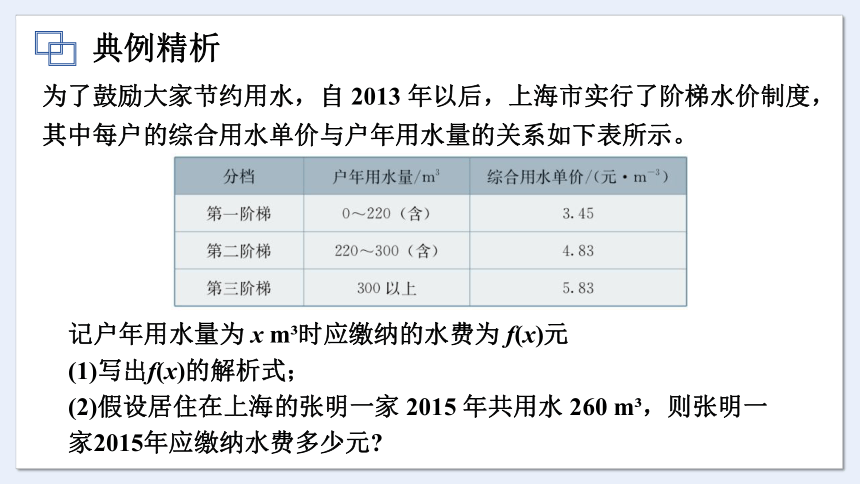
为了鼓励大家节约用水,自 2013 年以后,上海市实行了阶梯水价制度,其中每户的综合用水单价与户年用水量的关系如下表所示。
记户年用水量为 x m 时应缴纳的水费为 f(x)元
(1)写出f(x)的解析式;
(2)假设居住在上海的张明一家 2015 年共用水 260 m ,则张明一家2015年应缴纳水费多少元
解:(1) 不难看出, f(x)是一个分段函数,而且:
当0当220=4.83x-303.6;
当x>300 时,有
f(x)=220×3.45+(300-220)×4.83+(x-300)×5.83
=5.83x-603.6.
因此
f(x)=
3.45x,04.83x-303.6,2205.83x-603.6,x>300.
(2)因为 220<260≤300,所以
f(260)=4.83×260-303.6=952.2.
因此张明一家 2015 年应缴纳水费 952.2元。
由上题可知,可以用分段函数来描述生活中的阶梯水价、阶梯电价等内容。
典例精析
城镇化是国家现代化的重要指标,据有关资料显示,1978-2013年,我国城镇常住人口从1.7亿增加到7.3亿,假设每一年城镇常住人口的增加量都相等,记 1978 年后第t (限定t<40)年的城镇常住人口为 f(t)亿。写出f(t)的解析式,并由此估算出我国 2017 年的城镇常住人口数。
解:因为每一年城镇常住人口的增加量都相等,所以 f(t) 是一次函数,设 f(t)=kt+b,其中 k,b是常数。
注意到2013年是1978年后的第2013-1978=35 年,因此
即
f(0)=1.7,
f(35)=7.3,
b=1.7,
35k+6=7.3,
解得k=0.16,b=1.7。因此
f(t)=0.16t+1.7,t∈N且t<40.
又因为 2017 年是1978 年后的第2017-1978=39 年,而且
f(39)=0.16×39+1.7=7.94,
所以由此可估算出我国 2017 年的城镇常住人口为 7.94 亿。
典例精析
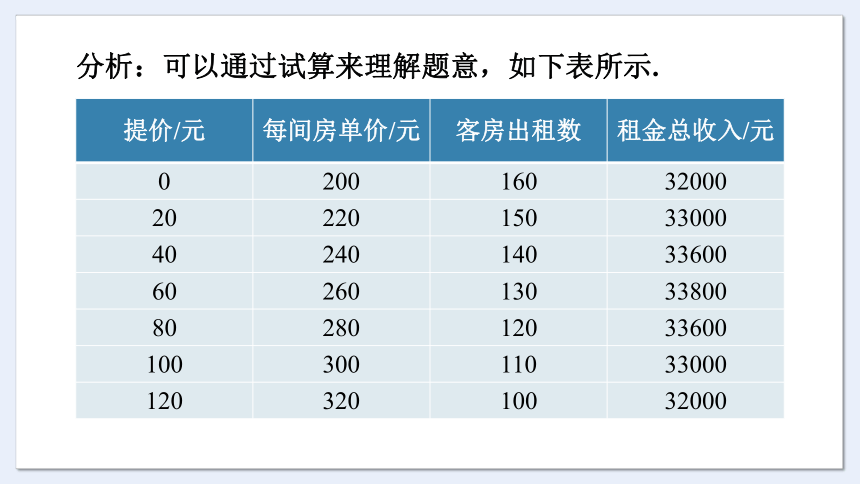
某农家旅游公司有客房 160 间,每间房单价为 200 元时,每天都客满。已知每间房单价每提高 20 元,则客房出租数就会减少 10 间。若不考虑其他因素,旅游公司把每间房单价提到多少时,每天客房的租金总收入最高
分析:可以通过试算来理解题意,如下表所示.
提价/元 每间房单价/元 客房出租数 租金总收入/元
0 200 160 32000
20 220 150 33000
40 240 140 33600
60 260 130 33800
80 280 120 33600
100 300 110 33000
120 320 100 32000
解:设每间房单价提高x个 20 元时,每天客房的租金总收入为 y 元。因为此时每间房单价为 200+20x 元,而客房出租数将减少10x间,即为 160-10x 间,所以
y=(200+20x)(160-10x)
=200(10+x)(16-x)
=200(-x2+6x+160)
=200[-(x-3)2+169]
=200(x-3)2+33 800.
从而可知,当 x=3 时,y 的最大值为 33 800。
因此每间房单价提到 200+20×3=260 元时,每天客房的租金总收入最高。
某单位计划用围墙围出一块矩形场地,现有材料可筑墙的总长度为l,如果要使围墙围出的场地面积最大,则矩形的长、宽各等于多少?
解:设矩形的长为x时,场地的面积为S。
典例精析
因为矩形的周长要为l,所以矩形的宽为(l-2x),由
x>0,
(l-2x)>0
可解得0<x<
又因为
S=(l-2x)x= -x +x= -(x-) +,
所以当x=, S的最大值为,此时矩形的宽为
(l-2×)=
即所围矩形是长、宽都为的正方形时,场地面积最大。
典例精析
已知某产品的总成本C与年产量Q之间的关系为 C=aQ +3 000,且当年产量是 100 时,总成本是 6 000.设该产品年产量为Q时的平均成本为 f(Q).
(1)求f(Q)的解析式;
(2)求年产量为多少时,平均成本最小,并求最小值.
解:(1)将Q=100,C=6 000代入 C=aQ +3 000 中,可得
100 a+3000=6 000,
从而a=,于是C= +3000
因此
f(Q)= = Q +, Q>0.
(2)因为
f(Q)= Q + ≥ 2 =60
且Q = ,即Q = 100时,上述等号成立。
因此,当年产量为 100 时,平均成本最小,且最小值为 60。
建模过程描述与介绍
俗话说,“物以稀为贵”。一般来说,当市面上某种商品的出售量比较多时,这种商品的价格就会比较低;而出售量比较少时,价格就会比较高。
例如,当市面上的苹果比较多时,苹果的价格就会降低。这时,如果利用一定的技术手段将苹果进行保鲜存储,等到市面上的苹果变少、价格上升之后再出售,则同样多的苹果就可以获得相对较高的销售收入,不过,需要注意的是,保鲜存储是有成本的,而且成本会随着时间的延长而增大。
针对上述这种日常生活中的现象,我们可以提出一些什么问题呢?
当然,我们可以探讨的问题很多。例如,为什么会发生这些现象?什么情况下不会发生这样的现象?能够利用哪些技术手段进行保鲜存储?哪种保鲜存储的成本最低?等等。类似的这些问题,因为不仅仅涉及量的关系,所以如果只用数学手段研究,将是十分困难的。
不过,上述现象中,涉及了量的增大与减少的问题,这可以用数学符号和语言进行描述。
仍以苹果为例,设市面上苹果的量为 x 万吨,苹果的单价为 y 元。上述现象说明,y会随着x的增大而减少,且 y 也会随着x的减少而增大——也就是说,如果y是x的函数并记作 y=f(x)的话, f(x)是减函数。
同样地,如果设保鲜存储的时间为 t 天,单位数量的保鲜存储成本为 C 元,且C是t的函数并记作 C=g(t) 的话, g(t)是一个增函数。
由于市面上苹果的量x会随着时间 t 的变化而变化,因此可以认为x是t的函数,并记作x=h(t)。从上面这些描述不难看出,在第t天出售苹果时,单位数量的苹果所获得的收益z元可以用t表示出来,即
z=y-C=f(x)-g(t)=f(h(t))-g(t).
此时,如果 f(x),g(t),h(t) 都是已知的,则能得到 z 与 t 的具体关系式。有了关系式之后,就能解决如下问题:z是否有最大值?如果z有最大值,那么 t 为多少时z取最大值?
怎样才能确定上述 f(x),g(t),h(t)呢?这可以通过合理假设以及收集数据、确定参数来完成。
例如,为了简单起见,我们可以假设 f(x) 和g(t)都是一次函数,且f(x)=k1x+l1,g(t)=k2t+l2;
并假设 h(t)是一个二次函数,且
h(t)=at2+bt+c.
则有z=f(h(t))-g(t)=k1at2+(k1b-k2)t+ k1c+ l1-l2,其中k1<0, k2>0,a≠0.
上述各参数可以通过收集实际数据来确定,例如,如果我们收集到了如下实际数据。
利用待定系数法,根据前面的假设就可以确定出
y=f(x)= -0.5x+5,
C=g(t)=0.01t+0.1,
x=h(t)=0.002t2-0.14t+9.6,
因此
z= -0.001t2-0.06t+0.1.
注意到上式可以改写成 z = -0.001(t-30)2+1,所以此时在t=30 时,z 取最大值 1。也就是说,在上述情况下,保鲜存储 30 天时,单位商品所获得的利润最大,为1元。
这样一来,我们就建立了一个决定苹果的最佳出售时间点的模型,并通过有关数据进行了说明。
当然,实际情况与上面的建模结果可能会出现偏差,因为我们假设f(x)和 g(t)都是一次函数等就已经把问题进行了简化,如果条件容许的话,可以先不假设函数的具体形式,在收集尽量多的数据的基础上,通过对数据的分析来最终得出函数的具体形式,这样也就能优化我们最终建立的模型。
以上我们用叙述的方式,让大家经历了一个简单的数学建模全过程。由此可以看出,对现实问题进行数学抽象,用数学语言表达问题、用数学方法构建模型解决问题就是数学建模,数学建模过程主要包括:在实际情境中从数学的视角发现问题、提出问题,分析问题、建立模型,确定参数、计算求解,验证结果、改进模型,最终解决实际问题。
在实际的数学建模过程中,为了向别人介绍数学建模的成果,给别人提供参考,我们还需要将建模结果整理成论文的形式。
一般来说,数学建模论文的结构可以按照建模过程来确定。例如,图1、图2、图3 所示都可以是数学建模论文的主体结构。
论文标题
一、发现问题、提出问题
二、分析问题、建立模型
三、确定参数、计算求解
四、验证结果、改进模型
图1
论文标题
一、问题的提出与分析
二、模型的建立与计算
三、问题的解决与反思
图2
论文标题
一、背景介绍
二、问题提出与分析
三、模型假设与符号说明
四、模型的建立
五、模型的求解
六、模型的检验
七、模型的评价
图3
当然,数学建模论文中还可以根据需要增加作者、摘要、参考文献、附录等信息。
需要提醒的是,对于一些综合性比较强的问题而言,数学建模的过程中需要做的事情比较多,比如数据收集与整理、模型试算、对比不同的模型、将结果以可视化方式展示、资料整理与论文撰写等,因此数学建模的过程中,往往采用分工合作的方式进行。一般来说,一个数学建模小组由 3~5人组成。理想的小组中,既要有数学基础扎实的同学,也要有能熟练使用计算机的同学,还要有写作表达能力强的同学。
基础自测
1.某地固定电话市话收费规定:前三分钟0.20元(不满三分钟按三分钟计算),以后每加一分钟增收0.10元(不满一分钟按一分钟计算),那么某人打市话550 s,应支付电话费( )
A.1.00元 B.0.90元
C.1.20元 D.0.80元
B
2.某厂有许多形状为直角梯形的铁皮边角料,为了降低消耗,现要从这些边角料上截取矩形铁片(如图所示).当截取的矩形面积最大时,矩形两边的长x,y应为( )
A.x=15,y=12
B.x=12,y=15
C.x=14,y=10
D.x=10,y=14
A
3.将进货单价为80元的商品按90元/个售出时,能卖出400个。已知该商品每个涨价1元时,其销售量就会减少20个。为了获得最大利润,其售价应定为( )
A.110元/个 B.105元/个
C.100元/个 D.95元/个
D
解析:设商品每个涨价x元,利润为y元,则销售量为(400-20x)个。
根据题意,得y=(10+x)(400-20x)=-20x2+200x+4 000=-20(x-5)2+4 500.
所以当x=5时,y取得最大值,最大值为4 500.
即当每个涨价5元,也就是售价为95元/个时,可以获得最大利润,故选D。
4.某游乐场每天的盈利额y(单位:元)与售出的门票数x(单位:张)之间的函数关系如图所示。试分析图像,要使该游乐场每天的盈利额超过1 000元,那么每天至少应售出______张门票。
234
典例剖析
一家报刊推销员从报社买进报纸的价格是每份0.20元,卖出的价格是每份0.30元,卖不完的还可以以每份0.08元的价格退回报社。在一个月(以30天计算)内有20天每天可卖出400份,其余10天每天只能卖出250份,但每天从报社买进报纸的份数都相同,问应该从报社买多少份报纸才能使每月所获得的利润最大?并计算每月最多能赚多少钱。
一次函数模型的应用
思路探究:本题所给条件较多,数量关系比较复杂,可以列表分析。
则y=6x+750+0.8x-200-6x=0.8x+550(250≤x≤400,x∈N+).
∵函数y=0.8x+550在x∈[250,400]上是增函数,
∴当x=400时,y取得最大值870.
即每天从报社买进400份报纸时,每月获得的利润最大,最大利润为870元。
归纳提升:实际问题中列出的函数关系式,要考虑实际问题对自变量的限制,即注意自变量的实际意义。对于与一次函数有关的最值问题通常借助一次函数的单调性结合定义域来处理。
对点训练
若一根蜡烛长20 cm,点燃后每小时燃烧5 cm,则燃烧剩下的高度h(cm)与燃烧时间t(h)的函数关系用图像表示为图中的( )
解析:蜡烛剩下的长度随时间增加而缩短,根据实际意义不可能是D;更不可能是A,C.故选B.
B
典例剖析
二次函数模型的应用
某水果批发商销售每箱进价为40元的苹果,假设每箱售价不得低于50元且不得高于55元。市场调查发现,若每箱以50元的价格销售,平均每天销售90箱,价格每提高1元,平均每天少销售3箱。
(1)求平均每天的销售量y(箱)与销售单价x(元/箱)之间的函数关系;
(2)求该批发商平均每天的销售利润w(元)与销售单价x(元/箱)之间的函数关系式;
(3)当每箱苹果的售价为多少元时,可以获得最大利润?最大利润是多少?
思路探究:本题中平均每天的销售量y(箱)与销售单价x(元/箱)是一个一次函数关系,虽然x∈[50,55],x∈N,但仍可把问题看成一次函数模型的应用问题;平均每天的销售利润w(元)与销售单价x(元/箱)是一个二次函数关系,可看成是一个二次函数模型的应用题。
解析:(1)根据题意,得y=90-3(x-50),
化简,得y=-3x+240(50≤x≤55,x∈N)。
(2)因为该批发商平均每天的销售利润=平均每天的销售量×每箱销售利润。
所以w=(x-40)(-3x+240)=-3x2+360x-9 600(50≤x≤55,x∈N)。
(3)因为w=-3x2+360x-9 600=-3(x-60)2+1 200,
所以当x<60时,w随x的增大而增大。
又50≤x≤55,x∈N,所以当x=55时,w有最大值,最大值为1 125。
所以当每箱苹果的售价为55元时,可以获得最大利润,且最大利润为1 125元。
归纳提升:二次函数的实际应用
1.在根据实际问题建立函数解析式后,可利用配方法、判别式法、换元法、函数的单调性等方法来求函数的最值,从而解决实际问题中最值问题,二次函数求最值最好结合二次函数的图像来解答。
2.对于本题要清楚平均每天的销售利润=平均每天的销售量×每箱销售利润。
对点训练
渔场中鱼群的最大养殖量为m(m>0),为了保证鱼群的生长空间,实际养殖量x应小于m,以便留出适当的空闲量。已知鱼群的年增长量y和实际养殖量与空闲率(空闲率是空闲量与最大养殖量的比值)的乘积成正比,比例系数为k(k>0)。
(1)写出y关于x的函数关系式,并指出该函数的定义域;
(2)求鱼群年增长量的最大值;
(3)当鱼群年增长量达到最大值时,求k的取值范围。
典例剖析
分段函数模型的应用
WAP手机上网每月使用量在500 min以下(包括500 min),按30元计费;超过500 min的部分按0.15元/min计费。假如上网时间过短(小于60min)使用量在1 min以下不计费,在1 min以上(包括1 min)按0.5元/min计费。WAP手机上网不收通话费和漫游费。
(1)写出上网时间x min与所付费用y元之间的函数关系式;
(2)12月份小王WAP上网使用量为20 h,要付多少钱?
(3)小王10月份付了90元的WAP上网费,那么他上网的时间是多少?
思路探究:由于上网时间不同,收费标准不同,因此对所付费用作分段讨论,以确定付费标准,建立函数关系式,解决付费与上网时间的问题。
(2)当x=20×60=1 200(min)时x>500,应付y=30+0.15×(1 200-500)=135(元)。
(3)90元已超过30元,所以上网时间超过500 min,由解析式可得上网时间为900 min。
归纳提升:应用分段函数时的三个注意点
(1)分段函数的“段”一定要分得合理,不重不漏。
(2)分段函数的定义域为对应每一段自变量取值范围的并集。
(3)分段函数的值域求法为:逐渐求函数值的范围,最后比较再下结论。
对点训练
大气温度y(℃)随着距离地面的高度x(km)的增加而降低,当在高度不低于11 km的高空时气温几乎不变.设地面气温为22 ℃,大约每上升1 km大气温度降低6 ℃,则y关于x的函数关系式为__________________.
典例剖析
对勾函数模型
归纳提升:求解本题的关键在于以建墙费用为目标函数建立函数关系式,而难点在于求函数的最小值,两种方案的函数式结构相似,但求最值方法不同,一个可用均值不等式求最值,而另一个则必须改用函数的单调性求最值。
对点训练
某单位用2 160万元购得一块空地,计划在该地块上建造一栋至少10层,每层2 000平方米的楼房。经测算,如果将楼房建为x(x≥10)层,则每平方米的平均建筑费用为560+48x(单位:元)。为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
完成课后相关练习
谢谢观看
谢谢观看
第三章 函数
3.3 函数的应用(一)
3.4 数学建模活动:
决定苹果的最佳出售时间点
基础知识
常见的函数模型
(1)一次函数模型
形如y=kx+b(k≠0)的函数模型是一次函数模型。应用一次函数的性质及图像解题时,应注意:
①一次函数有单调递增(一次项系数为正)和单调递减(一次项系数为负)两种情况;
②一次函数的图像是一条直线。
(2)二次函数模型
形如y=ax2+bx+c(a≠0)的函数模型是二次函数模型。二次函数模型是重要的数学模型之一,依据实际问题建立二次函数的解析式后,利用配方法求最值简单易懂,有时也可以依据二次函数的性质求最值,从而解决利润最大、用料最省等问题。
思考:一次、二次函数模型的定义域都是全体实数,在实际应用问题中,定义域一定是全体实数吗?
提示:不一定。在实际应用中,函数的自变量x往往具有实际意义,如x表示长度时,x≥0;x表示件数时,x≥0,且x∈Z等。在解答时,必须要考虑这些实际意义。
典例精析
为了鼓励大家节约用水,自 2013 年以后,上海市实行了阶梯水价制度,其中每户的综合用水单价与户年用水量的关系如下表所示。
记户年用水量为 x m 时应缴纳的水费为 f(x)元
(1)写出f(x)的解析式;
(2)假设居住在上海的张明一家 2015 年共用水 260 m ,则张明一家2015年应缴纳水费多少元
解:(1) 不难看出, f(x)是一个分段函数,而且:
当0
当x>300 时,有
f(x)=220×3.45+(300-220)×4.83+(x-300)×5.83
=5.83x-603.6.
因此
f(x)=
3.45x,0
(2)因为 220<260≤300,所以
f(260)=4.83×260-303.6=952.2.
因此张明一家 2015 年应缴纳水费 952.2元。
由上题可知,可以用分段函数来描述生活中的阶梯水价、阶梯电价等内容。
典例精析
城镇化是国家现代化的重要指标,据有关资料显示,1978-2013年,我国城镇常住人口从1.7亿增加到7.3亿,假设每一年城镇常住人口的增加量都相等,记 1978 年后第t (限定t<40)年的城镇常住人口为 f(t)亿。写出f(t)的解析式,并由此估算出我国 2017 年的城镇常住人口数。
解:因为每一年城镇常住人口的增加量都相等,所以 f(t) 是一次函数,设 f(t)=kt+b,其中 k,b是常数。
注意到2013年是1978年后的第2013-1978=35 年,因此
即
f(0)=1.7,
f(35)=7.3,
b=1.7,
35k+6=7.3,
解得k=0.16,b=1.7。因此
f(t)=0.16t+1.7,t∈N且t<40.
又因为 2017 年是1978 年后的第2017-1978=39 年,而且
f(39)=0.16×39+1.7=7.94,
所以由此可估算出我国 2017 年的城镇常住人口为 7.94 亿。
典例精析
某农家旅游公司有客房 160 间,每间房单价为 200 元时,每天都客满。已知每间房单价每提高 20 元,则客房出租数就会减少 10 间。若不考虑其他因素,旅游公司把每间房单价提到多少时,每天客房的租金总收入最高
分析:可以通过试算来理解题意,如下表所示.
提价/元 每间房单价/元 客房出租数 租金总收入/元
0 200 160 32000
20 220 150 33000
40 240 140 33600
60 260 130 33800
80 280 120 33600
100 300 110 33000
120 320 100 32000
解:设每间房单价提高x个 20 元时,每天客房的租金总收入为 y 元。因为此时每间房单价为 200+20x 元,而客房出租数将减少10x间,即为 160-10x 间,所以
y=(200+20x)(160-10x)
=200(10+x)(16-x)
=200(-x2+6x+160)
=200[-(x-3)2+169]
=200(x-3)2+33 800.
从而可知,当 x=3 时,y 的最大值为 33 800。
因此每间房单价提到 200+20×3=260 元时,每天客房的租金总收入最高。
某单位计划用围墙围出一块矩形场地,现有材料可筑墙的总长度为l,如果要使围墙围出的场地面积最大,则矩形的长、宽各等于多少?
解:设矩形的长为x时,场地的面积为S。
典例精析
因为矩形的周长要为l,所以矩形的宽为(l-2x),由
x>0,
(l-2x)>0
可解得0<x<
又因为
S=(l-2x)x= -x +x= -(x-) +,
所以当x=, S的最大值为,此时矩形的宽为
(l-2×)=
即所围矩形是长、宽都为的正方形时,场地面积最大。
典例精析
已知某产品的总成本C与年产量Q之间的关系为 C=aQ +3 000,且当年产量是 100 时,总成本是 6 000.设该产品年产量为Q时的平均成本为 f(Q).
(1)求f(Q)的解析式;
(2)求年产量为多少时,平均成本最小,并求最小值.
解:(1)将Q=100,C=6 000代入 C=aQ +3 000 中,可得
100 a+3000=6 000,
从而a=,于是C= +3000
因此
f(Q)= = Q +, Q>0.
(2)因为
f(Q)= Q + ≥ 2 =60
且Q = ,即Q = 100时,上述等号成立。
因此,当年产量为 100 时,平均成本最小,且最小值为 60。
建模过程描述与介绍
俗话说,“物以稀为贵”。一般来说,当市面上某种商品的出售量比较多时,这种商品的价格就会比较低;而出售量比较少时,价格就会比较高。
例如,当市面上的苹果比较多时,苹果的价格就会降低。这时,如果利用一定的技术手段将苹果进行保鲜存储,等到市面上的苹果变少、价格上升之后再出售,则同样多的苹果就可以获得相对较高的销售收入,不过,需要注意的是,保鲜存储是有成本的,而且成本会随着时间的延长而增大。
针对上述这种日常生活中的现象,我们可以提出一些什么问题呢?
当然,我们可以探讨的问题很多。例如,为什么会发生这些现象?什么情况下不会发生这样的现象?能够利用哪些技术手段进行保鲜存储?哪种保鲜存储的成本最低?等等。类似的这些问题,因为不仅仅涉及量的关系,所以如果只用数学手段研究,将是十分困难的。
不过,上述现象中,涉及了量的增大与减少的问题,这可以用数学符号和语言进行描述。
仍以苹果为例,设市面上苹果的量为 x 万吨,苹果的单价为 y 元。上述现象说明,y会随着x的增大而减少,且 y 也会随着x的减少而增大——也就是说,如果y是x的函数并记作 y=f(x)的话, f(x)是减函数。
同样地,如果设保鲜存储的时间为 t 天,单位数量的保鲜存储成本为 C 元,且C是t的函数并记作 C=g(t) 的话, g(t)是一个增函数。
由于市面上苹果的量x会随着时间 t 的变化而变化,因此可以认为x是t的函数,并记作x=h(t)。从上面这些描述不难看出,在第t天出售苹果时,单位数量的苹果所获得的收益z元可以用t表示出来,即
z=y-C=f(x)-g(t)=f(h(t))-g(t).
此时,如果 f(x),g(t),h(t) 都是已知的,则能得到 z 与 t 的具体关系式。有了关系式之后,就能解决如下问题:z是否有最大值?如果z有最大值,那么 t 为多少时z取最大值?
怎样才能确定上述 f(x),g(t),h(t)呢?这可以通过合理假设以及收集数据、确定参数来完成。
例如,为了简单起见,我们可以假设 f(x) 和g(t)都是一次函数,且f(x)=k1x+l1,g(t)=k2t+l2;
并假设 h(t)是一个二次函数,且
h(t)=at2+bt+c.
则有z=f(h(t))-g(t)=k1at2+(k1b-k2)t+ k1c+ l1-l2,其中k1<0, k2>0,a≠0.
上述各参数可以通过收集实际数据来确定,例如,如果我们收集到了如下实际数据。
利用待定系数法,根据前面的假设就可以确定出
y=f(x)= -0.5x+5,
C=g(t)=0.01t+0.1,
x=h(t)=0.002t2-0.14t+9.6,
因此
z= -0.001t2-0.06t+0.1.
注意到上式可以改写成 z = -0.001(t-30)2+1,所以此时在t=30 时,z 取最大值 1。也就是说,在上述情况下,保鲜存储 30 天时,单位商品所获得的利润最大,为1元。
这样一来,我们就建立了一个决定苹果的最佳出售时间点的模型,并通过有关数据进行了说明。
当然,实际情况与上面的建模结果可能会出现偏差,因为我们假设f(x)和 g(t)都是一次函数等就已经把问题进行了简化,如果条件容许的话,可以先不假设函数的具体形式,在收集尽量多的数据的基础上,通过对数据的分析来最终得出函数的具体形式,这样也就能优化我们最终建立的模型。
以上我们用叙述的方式,让大家经历了一个简单的数学建模全过程。由此可以看出,对现实问题进行数学抽象,用数学语言表达问题、用数学方法构建模型解决问题就是数学建模,数学建模过程主要包括:在实际情境中从数学的视角发现问题、提出问题,分析问题、建立模型,确定参数、计算求解,验证结果、改进模型,最终解决实际问题。
在实际的数学建模过程中,为了向别人介绍数学建模的成果,给别人提供参考,我们还需要将建模结果整理成论文的形式。
一般来说,数学建模论文的结构可以按照建模过程来确定。例如,图1、图2、图3 所示都可以是数学建模论文的主体结构。
论文标题
一、发现问题、提出问题
二、分析问题、建立模型
三、确定参数、计算求解
四、验证结果、改进模型
图1
论文标题
一、问题的提出与分析
二、模型的建立与计算
三、问题的解决与反思
图2
论文标题
一、背景介绍
二、问题提出与分析
三、模型假设与符号说明
四、模型的建立
五、模型的求解
六、模型的检验
七、模型的评价
图3
当然,数学建模论文中还可以根据需要增加作者、摘要、参考文献、附录等信息。
需要提醒的是,对于一些综合性比较强的问题而言,数学建模的过程中需要做的事情比较多,比如数据收集与整理、模型试算、对比不同的模型、将结果以可视化方式展示、资料整理与论文撰写等,因此数学建模的过程中,往往采用分工合作的方式进行。一般来说,一个数学建模小组由 3~5人组成。理想的小组中,既要有数学基础扎实的同学,也要有能熟练使用计算机的同学,还要有写作表达能力强的同学。
基础自测
1.某地固定电话市话收费规定:前三分钟0.20元(不满三分钟按三分钟计算),以后每加一分钟增收0.10元(不满一分钟按一分钟计算),那么某人打市话550 s,应支付电话费( )
A.1.00元 B.0.90元
C.1.20元 D.0.80元
B
2.某厂有许多形状为直角梯形的铁皮边角料,为了降低消耗,现要从这些边角料上截取矩形铁片(如图所示).当截取的矩形面积最大时,矩形两边的长x,y应为( )
A.x=15,y=12
B.x=12,y=15
C.x=14,y=10
D.x=10,y=14
A
3.将进货单价为80元的商品按90元/个售出时,能卖出400个。已知该商品每个涨价1元时,其销售量就会减少20个。为了获得最大利润,其售价应定为( )
A.110元/个 B.105元/个
C.100元/个 D.95元/个
D
解析:设商品每个涨价x元,利润为y元,则销售量为(400-20x)个。
根据题意,得y=(10+x)(400-20x)=-20x2+200x+4 000=-20(x-5)2+4 500.
所以当x=5时,y取得最大值,最大值为4 500.
即当每个涨价5元,也就是售价为95元/个时,可以获得最大利润,故选D。
4.某游乐场每天的盈利额y(单位:元)与售出的门票数x(单位:张)之间的函数关系如图所示。试分析图像,要使该游乐场每天的盈利额超过1 000元,那么每天至少应售出______张门票。
234
典例剖析
一家报刊推销员从报社买进报纸的价格是每份0.20元,卖出的价格是每份0.30元,卖不完的还可以以每份0.08元的价格退回报社。在一个月(以30天计算)内有20天每天可卖出400份,其余10天每天只能卖出250份,但每天从报社买进报纸的份数都相同,问应该从报社买多少份报纸才能使每月所获得的利润最大?并计算每月最多能赚多少钱。
一次函数模型的应用
思路探究:本题所给条件较多,数量关系比较复杂,可以列表分析。
则y=6x+750+0.8x-200-6x=0.8x+550(250≤x≤400,x∈N+).
∵函数y=0.8x+550在x∈[250,400]上是增函数,
∴当x=400时,y取得最大值870.
即每天从报社买进400份报纸时,每月获得的利润最大,最大利润为870元。
归纳提升:实际问题中列出的函数关系式,要考虑实际问题对自变量的限制,即注意自变量的实际意义。对于与一次函数有关的最值问题通常借助一次函数的单调性结合定义域来处理。
对点训练
若一根蜡烛长20 cm,点燃后每小时燃烧5 cm,则燃烧剩下的高度h(cm)与燃烧时间t(h)的函数关系用图像表示为图中的( )
解析:蜡烛剩下的长度随时间增加而缩短,根据实际意义不可能是D;更不可能是A,C.故选B.
B
典例剖析
二次函数模型的应用
某水果批发商销售每箱进价为40元的苹果,假设每箱售价不得低于50元且不得高于55元。市场调查发现,若每箱以50元的价格销售,平均每天销售90箱,价格每提高1元,平均每天少销售3箱。
(1)求平均每天的销售量y(箱)与销售单价x(元/箱)之间的函数关系;
(2)求该批发商平均每天的销售利润w(元)与销售单价x(元/箱)之间的函数关系式;
(3)当每箱苹果的售价为多少元时,可以获得最大利润?最大利润是多少?
思路探究:本题中平均每天的销售量y(箱)与销售单价x(元/箱)是一个一次函数关系,虽然x∈[50,55],x∈N,但仍可把问题看成一次函数模型的应用问题;平均每天的销售利润w(元)与销售单价x(元/箱)是一个二次函数关系,可看成是一个二次函数模型的应用题。
解析:(1)根据题意,得y=90-3(x-50),
化简,得y=-3x+240(50≤x≤55,x∈N)。
(2)因为该批发商平均每天的销售利润=平均每天的销售量×每箱销售利润。
所以w=(x-40)(-3x+240)=-3x2+360x-9 600(50≤x≤55,x∈N)。
(3)因为w=-3x2+360x-9 600=-3(x-60)2+1 200,
所以当x<60时,w随x的增大而增大。
又50≤x≤55,x∈N,所以当x=55时,w有最大值,最大值为1 125。
所以当每箱苹果的售价为55元时,可以获得最大利润,且最大利润为1 125元。
归纳提升:二次函数的实际应用
1.在根据实际问题建立函数解析式后,可利用配方法、判别式法、换元法、函数的单调性等方法来求函数的最值,从而解决实际问题中最值问题,二次函数求最值最好结合二次函数的图像来解答。
2.对于本题要清楚平均每天的销售利润=平均每天的销售量×每箱销售利润。
对点训练
渔场中鱼群的最大养殖量为m(m>0),为了保证鱼群的生长空间,实际养殖量x应小于m,以便留出适当的空闲量。已知鱼群的年增长量y和实际养殖量与空闲率(空闲率是空闲量与最大养殖量的比值)的乘积成正比,比例系数为k(k>0)。
(1)写出y关于x的函数关系式,并指出该函数的定义域;
(2)求鱼群年增长量的最大值;
(3)当鱼群年增长量达到最大值时,求k的取值范围。
典例剖析
分段函数模型的应用
WAP手机上网每月使用量在500 min以下(包括500 min),按30元计费;超过500 min的部分按0.15元/min计费。假如上网时间过短(小于60min)使用量在1 min以下不计费,在1 min以上(包括1 min)按0.5元/min计费。WAP手机上网不收通话费和漫游费。
(1)写出上网时间x min与所付费用y元之间的函数关系式;
(2)12月份小王WAP上网使用量为20 h,要付多少钱?
(3)小王10月份付了90元的WAP上网费,那么他上网的时间是多少?
思路探究:由于上网时间不同,收费标准不同,因此对所付费用作分段讨论,以确定付费标准,建立函数关系式,解决付费与上网时间的问题。
(2)当x=20×60=1 200(min)时x>500,应付y=30+0.15×(1 200-500)=135(元)。
(3)90元已超过30元,所以上网时间超过500 min,由解析式可得上网时间为900 min。
归纳提升:应用分段函数时的三个注意点
(1)分段函数的“段”一定要分得合理,不重不漏。
(2)分段函数的定义域为对应每一段自变量取值范围的并集。
(3)分段函数的值域求法为:逐渐求函数值的范围,最后比较再下结论。
对点训练
大气温度y(℃)随着距离地面的高度x(km)的增加而降低,当在高度不低于11 km的高空时气温几乎不变.设地面气温为22 ℃,大约每上升1 km大气温度降低6 ℃,则y关于x的函数关系式为__________________.
典例剖析
对勾函数模型
归纳提升:求解本题的关键在于以建墙费用为目标函数建立函数关系式,而难点在于求函数的最小值,两种方案的函数式结构相似,但求最值方法不同,一个可用均值不等式求最值,而另一个则必须改用函数的单调性求最值。
对点训练
某单位用2 160万元购得一块空地,计划在该地块上建造一栋至少10层,每层2 000平方米的楼房。经测算,如果将楼房建为x(x≥10)层,则每平方米的平均建筑费用为560+48x(单位:元)。为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
完成课后相关练习
谢谢观看
谢谢观看
