总复习学案(山东省济南市历下区)

《变量之间的关系》专项练习
学习本章，重点是要区分变量和常量以及变量中的自变量和因变量．因变量是随着自变量和因变量的变化而变化的，表示变量之间的关系有三种：表格、关系式和图象．下面就本章内容分考点列举例题及练习如下：
考点一 理解表格刻画的变量之间的关系和用表格来刻画变量之间的关系
【例1】某公园决定投资开发新项目，通过考察确定有6个项目可供选择，各项目所需资金及预计年利润如下表：
（1）上表反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？
（2）如果投资一个4亿元的项目，那么其年利润预计有多少？
（3）如果要预计获得0.9千万元的年利润,投资一个项目需要多少资金
(4)如果该公司可以拿出10亿元进行多个项目的投资,预计最大年利润是多少
【反思】本题要求同学们能从表格中分析出某些变量之间的关系，并能根据表格信息进行简单的计算，发展有条理的进行思考和表达的能力．
专项练习
1．据世界人口组织公布，世界上的人口从1600年到1999年一直呈递增状态，即随着时间的变化，地球上人口数量在逐渐增加，如果用t表示时间，表示人口数量， 是自变量， 是因变量.
2．某商场出售某种商品，其销售件数与售价的关系如下表：
销售件数/件 1 2 3 4 5 ……
售价/元 8.4 16.8 25.2 33.6 42 ……
（1）上述表格中哪些量在变化？自变量和因变量各是什么？
（2）某顾客欲购买这种货物10件，但他只带了80元钱，你能知道他所带的钱是否够用？如果不够用，则最多可购买该货物多少件？
3.下表是红星电视机厂2002年前半年每个月的产量：
x/月 1 2 3 4 5 6
y/月 9 000 9 000 12 000 14 000 16 000 20 000
（1） 随着x的变化，y的变化趋势是什么？
（2） 由上表，你知道哪几个月的月产量保持不变？哪几个月月产量在匀速增长？哪几个月产量最高？
（3） 试求2002年前半年的平均月产量是多少？
考点二 根据已知条件确定关系式，利用关系式求值
【例2】（2006·辽宁十一市非课改,有改动）某蔬菜基地加工厂有工人100人，现对100人进行工作分工，或采摘蔬菜，或对当日采摘的蔬菜进行精加工．每人每天只能做一项工作．若采摘蔬菜，每人每天平均采摘48kg；若对采摘后的蔬菜进行精加工，每人每天可精加工32kg（每天精加工的蔬菜和没来得及精加工的蔬菜全部售出）．已知每千克蔬菜直接出售可获利润1元，精加工后再出售，每千克可获利润3元．设每天安排名工人进行蔬菜精加工．
（1）求每天蔬菜精加工后再出售所得利润（元）与（人）的关系式；
（2）如果每天精加工的蔬菜和没来得及精加工的蔬菜全部售出的利润为元，求与的关系式;
(3) 安排10名工人进行蔬菜精加工,能获得多少利润
(4)厂方预算部门经过核算他们最多能获得5760元利润,聪明的你想一想,需要安排多少名工人进行蔬菜精加工
【点评】本题着重考查学生分析问题、探求关系式、并代入求值．解这类问题时要求学生熟练掌握理解变量之间的纵横关系，还要有一定的生活常识．
专项练习
1． 设地面气温为20℃，如果每升高1千米，气温下降6℃
（1） 在这个变化过程中，自变量是_____，因变量是_____；
（2） 如果高度用h（千米）表示，气温用t（）表示，那么t随h的变化而变化的关系式为_____；
（3） 高度h=10千米时，气温是_____．
2． 拖拉机工作时，油箱中的余油量Q（升）与工作时间t（小时）的关系，可用Q=40-6t来表示，当t=2时，Q=_____；当t=5时，Q=_____．
3． 圆柱的底面半径是3cm，则圆柱的体积y(cm3)与圆柱的高x(cm)之间的关系式可记为_____．
4． 如果长方形的一边长为8，另一边长为x,此长方形的面积为y.
（1）长方形的面积y与x之间关系式是什么？
(2) 当x=8时，y的值是多少？此时它表示什么图形？
5． 商店出售一种瓜子，数量x（克）与售价c（元）之间的关系如下表：
数量x/克 售价c/元
100 0.9+0.1
200 1.8+0.1
300 2.7+0.1
400 3.6+0.1
表中售价栏中的0.10是塑料袋的价钱℃
(1) 写出售价c（元）与数量x（克）之间的关系式；
(3) 当数量 由1千克变化到3千克时，售价的变化范围是多少元？
8. 圆柱的高是10cm，圆柱底圆的半径为r cm,圆柱的侧面展开图的面积Scm2 ．写出圆柱侧面展开图的面积S与圆柱底面半径r之间的关系式．
考点三 从图象中获取和辨别信息
【例3】一根蜡烛长20cm，点燃后每小时燃烧5cm，燃烧时剩下的长度为y(cm)与燃烧时间x（小时）的关系用图象表示为下图中的（　　）
【解析】根据常识,知道随着燃烧时间变化,蜡烛长度会相应越来越短,而且这是一道实际问题,一次函数图象为一线段,选项A与实际情况相反,选项C表示蜡烛长度在燃烧长度不变,选项D没考虑实际意义,自变量有取值范围,图象应为线段.故选B.
专项练习
1．如图是桂林冬季某一天的气温随时间变化的图像，请根据图像填空：在 时气温最低，最低气温为 ℃当天最高气温是 ℃，在 时达到；这一天的温差是 ℃（所有结果均取整数）．
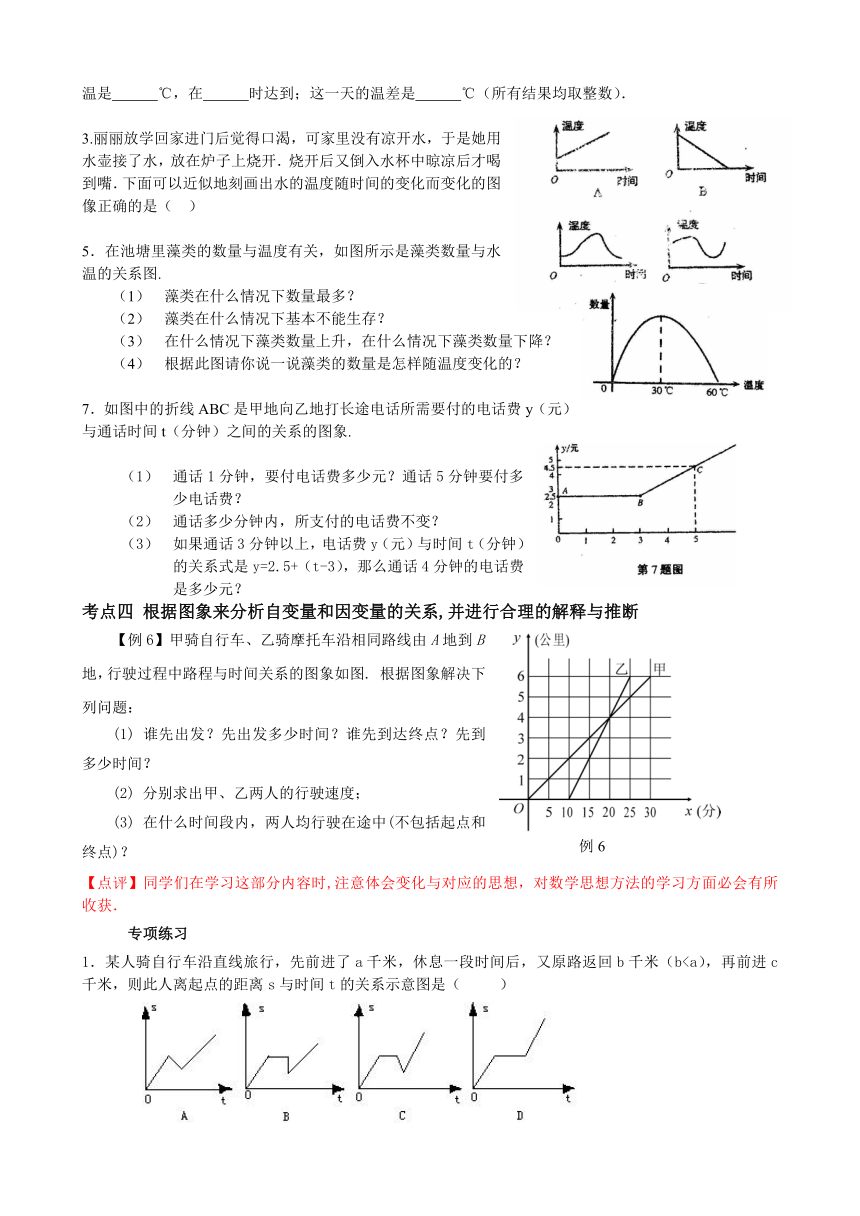
3.丽丽放学回家进门后觉得口渴，可家里没有凉开水，于是她用水壶接了水，放在炉子上烧开．烧开后又倒入水杯中晾凉后才喝到嘴．下面可以近似地刻画出水的温度随时间的变化而变化的图像正确的是（ ）
5．在池塘里藻类的数量与温度有关，如图所示是藻类数量与水温的关系图.
（1） 藻类在什么情况下数量最多？
（2） 藻类在什么情况下基本不能生存？
（3） 在什么情况下藻类数量上升，在什么情况下藻类数量下降？
（4） 根据此图请你说一说藻类的数量是怎样随温度变化的？
7．如图中的折线ABC是甲地向乙地打长途电话所需要付的电话费y（元）与通话时间t（分钟）之间的关系的图象.
（1） 通话1分钟，要付电话费多少元？通话5分钟要付多少电话费？
（2） 通话多少分钟内，所支付的电话费不变？
（3） 如果通话3分钟以上，电话费y（元）与时间t（分钟）的关系式是y=2.5+（t-3），那么通话4分钟的电话费是多少元？
考点四 根据图象来分析自变量和因变量的关系,并进行合理的解释与推断
【例6】甲骑自行车、乙骑摩托车沿相同路线由A地到B地，行驶过程中路程与时间关系的图象如图. 根据图象解决下列问题：
(1) 谁先出发？先出发多少时间？谁先到达终点？先到多少时间？
(2) 分别求出甲、乙两人的行驶速度；
(3) 在什么时间段内，两人均行驶在途中(不包括起点和终点)？
【点评】同学们在学习这部分内容时,注意体会变化与对应的思想，对数学思想方法的学习方面必会有所收获．
专项练习
1．某人骑自行车沿直线旅行，先前进了a千米，休息一段时间后，又原路返回b千米（b2． 如图⑩是小陈同学骑自行车上学的路程与时间的关系图，请你根据图像描述他上学路上的情形．
3．小刚、爸爸、爷爷同时同家中出发到达同一目的地后都立即返回，小刚去时骑自行车，返回时步行，爷爷去时步行，返回时骑自行车，爸爸往返都是步行．三人步行的速度不等，小刚与爷爷骑车速度相等，每个人离家的距离与行走的时间的关系，分别是下图中的一个，走完一个往返．问：
（1） 小刚、爸爸、爷爷往返各用了多少分钟？
（2） 他们三人的步行速度分别是多少？你能求出来吗？
4．某学校进行往返跑比赛，张佳同学去时以每秒6m的平均速度跑完，回来时以每秒5m的速度跑回起点，时间与速度的变化如图所示.
（1） 张佳共跑了多长时间？
（2） 哪些时段保持匀速？速度分别是多少？
（3） 试写出她在跑步过程中，离起点距离S（m）与时间t（s）之间的关系式？
一、小车下滑的时间
1．根据世界人口组织公布，地球上的人口从年到年一直呈递增趋势，即随着时间的变化，地球上的人口数量在逐渐地增加，在这个变化过程中_____是自变量．
2．小亮帮母亲预算家庭月份电费开支情况，下表是小亮家月初连续天每天早上电表显示的读数．
日期 1 2 3 4 5 6 7 8
电表读数 21 24 28 33 39 42 46 49
（1）表格中反映的变量是______，自变量是______，因变量是______．
（2）估计小亮家月份的用电量是______度，若每度电电费是元，估计他家月份应交的电费是______元．
3．一空水池现需注满水，水池深，现以不变的流量注水，数据如下：
水的深度
注水时间
（1）此题中流量是不是变量？
（2）找出自变量、因变量？
（3）你能推断出注满水所需的时间吗？
4．下表是小华做观察水的沸腾试验时所记录的数据：
时间（分） 0 1 2 3 4 5 6 7 8 9 10 11 12
温度（℃） 60 65 70 75 80 85 90 95 100 100 100 100 100
（1）时间是分钟时，水的温度为多少？
（2）此表反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？
（3）在这段时间内，水的温度是怎样随时间变化的？
5．某瓜果基地市场部为指导该基地某种蔬菜的生产和销售，在对历年市场行情和生产情况进行了调查的基础上，对今年这种蔬菜上市后的市场售价和生产成本进行了预测，获得每千克蔬菜的利润与月份的关系如下（“－”表示亏损）：
月份 2 3 4 5 6 7 8
利润（元／千克）
（1）从表上的趋势看，在今年哪几个月生产和出售这种蔬菜会亏损？在哪几个月生产和出售这种蔬菜会获利？你认为应该在几月份生产和销售这种蔬菜最好？
（2）如果5月份该瓜果基地生产这种蔬菜吨，则月份该基地可获得多少利润？
二、变化中的三角形
1．已知，如图1，一轮船在离港千米的地出发向港匀速行驶，分钟后离港千米（未到达港）．设小时后，轮船离港千米（未到达港），则与之间的关系式为______．
2．如图2，圆柱的底面半径是厘米，当圆柱的高由小到大变化时，圆柱的体积也随之发生了变化．（1）在这个变化中，自变量是______，因变量是______；（2）如果圆柱的高为（厘米），圆柱的体积是（厘米）与的关系为______；（3）当高由厘米变化到厘米时，圆柱的体积由____厘米变化到___厘米．
3．如图3，在中，过顶点的直线与边相交于点，当顶点沿直线向点运动，且越过点后逐渐远离后，在这一运动过程中，的面积的变化情况是（　　）
Ａ．由大变小Ｂ．由小变大Ｃ．先由大变小，后由小变大 Ｄ．先由小变大，后由大变小
4．一位卖报人从报社每天因定购买份报纸，报纸每份定价元．卖报人从报社买报时按付款，按原价卖出．但如果报纸卖不出去退回报社时，报社只退给他的款项．如果卖报人卖出的报数为，所获得利润为，试写出与的关系式．如果卖报人某天既未获利，也未亏本，他一共卖出了多少份报？
三、温度的变化
1．某托运公司托运行李的费用与托运行李的重量关系如图所示．由图4可知行李的重量只要不超过______千克，就可免费托运，行李的重为千克时收费______元，行李的重量年增加千克多收费______元．
2．为发展电信事业，方便用户，电信公司对移动电话采用不同的收费方式，其中所使用的“便民卡”和“如意卡”在该市所在范围内每月（30天）的通话时间（分钟）与通话费（元）的关系如图5所示，若某人每月通话时间为分钟，你选择哪种卡合适．
Ａ．便民卡 Ｂ．如意卡 Ｃ．两种费用相同 Ｄ．无法比较
3．如图6所示，是某港口从上午时到下午时的水深情况，根据图回答下列问题：
（1）在时到时，这段时间内大约什么时间港口的水位最深，深度是多少米？
（2）大约什么时候港口的水位置线，是多少？
（3）在这段时间里，水深是如何变化的？
4．图7是由权威机构发布的，在1993年4月～2005年4月期间由中国经济状况指标之一中国经济预警指数绘制的图表．
（1）请你仔细阅读图表，可从图表中得出：
我国经济发展过冷的最低点出现在____年；我国经济发展过冷的最低点出现在____年．
（2）根据该图表提供的信息，请你简单描述我国从1993年4月到2005年4月经济发展状况．
5．在池塘里藻类的数量与温度有关，如图8所示是藻类数量与水温的关系图．
（1）藻类在什么情况下数量最多？
（2）藻类在什么情况下基本不能生存？
（3）在什么情况下藻类数量上升，在什么情况下藻类数量下降？
（4）根据如图8所示，请说一说藻类的数量是怎样随温度变化的？
四、速度的变化
1．假定甲、乙两人在一次赛跑中，路程与时间的关系如图9所示，我们可以知道：（1）这是一次____米跑；（2）甲、乙两人中____先到达终点；（3）乙在这次赛跑中速度为____米／秒．
2．某开发区为了解决居民住房条件，对每年年底人口总数和人均住房面积的统计结果分别作图（图10－（1）为某开发区每年年底人口总数统计折线图，图10－（2）为某开发区每年年底人均面积统计图）．
（1）试根据图中折线图所提供的信息完成下面统计表格：
项目 1999年 2000年 2001年
人均住房面积／米
人口总数／万人
该市住房总面积／万平方米
（2）该开发区2000年和2001年两年中，哪一年增加的住房面积多？多增加多少万平方米？
3．如图11所示，折线表示某个实际问题的图象，请你编写一道符合该图象意义的情境．
20
y
4
x
O
D、
20
y
4
x
O
C、
20
y
4
x
O
B、
20
y
4
x
O
A、
例6