一次函数复习

一次函数
【核心复习】
一次函数的图象和性质是中考的热点。根据已知条件利用待定系数法确定一次函数表达式是本单元的重点，它是利用一次函数解决一切实际问题的基础。一次函数与一元一次方程、一元一次不等式及二元一次方程组有密切的联系，是数形结合思想、函数思想及函数模型的重要体现。
本单元主要复习以下内容
1、一次函数的图象和性质：
（1） 一次函数图象所经过的象限与k,b的符号关系：
k＞0,b>0时，图像在一、二、三象限；K>0,b<0时，图像在一、三、四象限；
k <0,b>0时，图像在一、二、四象限；K<0,b<0时，图像在二、三、四象限
反之，亦成立
（2） 一次函数的增减性：
k＞0时，y随x的增大而 增大 ；k <0 ，y随x的增大而 减小 。
（3） 一次函数与两坐标轴的交点坐标：
一次函数y=kx+b（k≠0）的图象与x轴的交于点（ ，0），
与y轴交于点（0，b）。
2、确定一次函数表达式
确定一次函数表达式常见有以下两种题型：
根据实际问题直接获得表达式；根据点的坐标利用待定系数法确定。
3、一次函数与一元一次方程、一元一次不等式的关系.
4、一次函数与二元一次方程、二元一次方程组的关系：
二元一次方程的解是相应的一 次函数图象上的点；
二元一次方程组的解是相应的两条直线的交点；当二元一次方程组有唯一解时，两直线相交；当二元一次方程组没有解时，两直线平行；当二元一次方程组有无数解时，两直线重合。
求两条直线的交点即转化为求二元一次方程组的解。
知识结构网络:
【思维体验】
一、一次函数的图象和性质
1、 （2006年青岛）点 是一次函数y=-4x+3图象上的两个点，且 ＜ , 则 与 的大小关系是（ A ）
A． > B． > >0 C． < D． ＝
2、无论m为何实数，直线y=2x+m与y=－x+4的交点不可能在（ C ）
A、第一象限 B、第二象限 C、第三象限 D、第四象限
3、（2006年江阴）已知为非0实数，且满足，则一次函数的图象一定经过 （ ）
A．第一、二、三象限 B．第二、四象限 C．第一象限 D．第二象限
4、已知一次函数
（1） m为何值时，它的图象经过点（一1，3）？
（2） m为何值时，它的图象与y轴交点在x轴下方？
（3） m为何值时，它的图象平行于直线 ？
解：（1）把（一1，3）代入表达式得解得m=0（2）由函数的图象与y轴交点在x轴下方，可得,即m>2（3）由函数的图象平行于直线 ，可得解得
【反思与小结】明确一次函数y=kx+b(k≠0)中的k,b各自的作用，以及k,b的符号共同决定了直线的大致位置。
二、和实际问题有关的一次函数问题
1、 （2007浙江嘉兴）周日上午，小俊从外地乘车回嘉兴．一路上，小俊记下了如下数据：
观察时间 9∶00（t＝0） 9∶06（t＝6） 9∶18（t＝18）
路牌内容 嘉兴90km 嘉兴80km 嘉兴60km
（注：“嘉兴90km”表示离嘉兴的距离为90千米）
假设汽车离嘉兴的距离s（千米）是行驶时间t（分钟）的一次函数，求s关于t的函数关系式．
解：设s＝kt＋b，则，解得：，所以s＝－＋90
2、（2007浙江温州）为调动销售人员的积极性，A、B两公司采取如下工资支付方式：A公司每月2000元基本工资，另加销售额的2%作为奖金；B公司每月1600元基本工资，另加销售额的4%作为奖金。已知A、B公司两位销售员小李、小张1～6月份的销售额如下表：
月份销售额 销售额（单位：元）
1月 2月 3月 4月 5月 6月
小李（A公司） 11600 12800 14000 15200 16400 17600
小张（B公司 7400 9200 1100 12800 14600 16400
(1)请问小李与小张3月份的工资各是多少？
(2)小李1～6月份的销售额与月份的函数关系式是小张1～6月份的销售额也是月份的一次函数，请求出与的函数关系式；
(3)如果7～12月份两人的销售额也分别满足（2）中两个一次函数的关系，问几月份起小张的工资高于小李的工资。
解：（1）小李3月份工资＝2000＋2%×14000＝2280（元）
　　　　小张3月份工资＝1600＋4%×11000＝2040（元）
（2）设，取表中的两对数（1，7400），（2，9200）代入解析式，得
（3）小李的工资
小李的工资
当小李的工资
解得，x>8
答：从9月份起，小张的工资高于小李的工资。
3．(06河北)甲、乙两个工程队分别同时开挖两段河渠，所挖河渠的长度与挖掘时间之间的关系如图11所示，请根据图象所提供的信息解答下列问题：
（1）乙队开挖到30m时，用了　　　　h．
开挖6h时甲队比乙队多挖了　　　m；
（2）请你求出：①甲队在的时段内，与之间的函数关系式；
②乙队在的时段内，与之间的函数关系式；
（3）当为何值时，甲、乙两队在施工过程中所挖河渠的长度相等？
解：（1）2，10；
　 （2）设甲队在的时段内与之间的函数关系式为，
　　　 由图可知，函数图象过点，　，解得，．
　　　 设乙队在的时段内与之间的函数关系式为，
　　　 由图可知，函数图象过点，
　　　解得．
（3）由题意，得，解得（h）．
　　　当为4h时，甲、乙两队所挖的河渠长度相等．
【反思与小结】一次函数在社会生活中的应用题，会通过表格或图象读取信息，得到两个条件确定一次函数表达式。会通过解二元一次方程组求两条直线的交点坐标。注意分类讨论的数学思想方法．
三、一次函数与一元一次方程、一元一次不等式
1．（07玉林市）某化妆公司每月付给销售人员的工资有两种方案．
方案一：没有底薪，只拿销售提成；
方案二：底薪加销售提成．
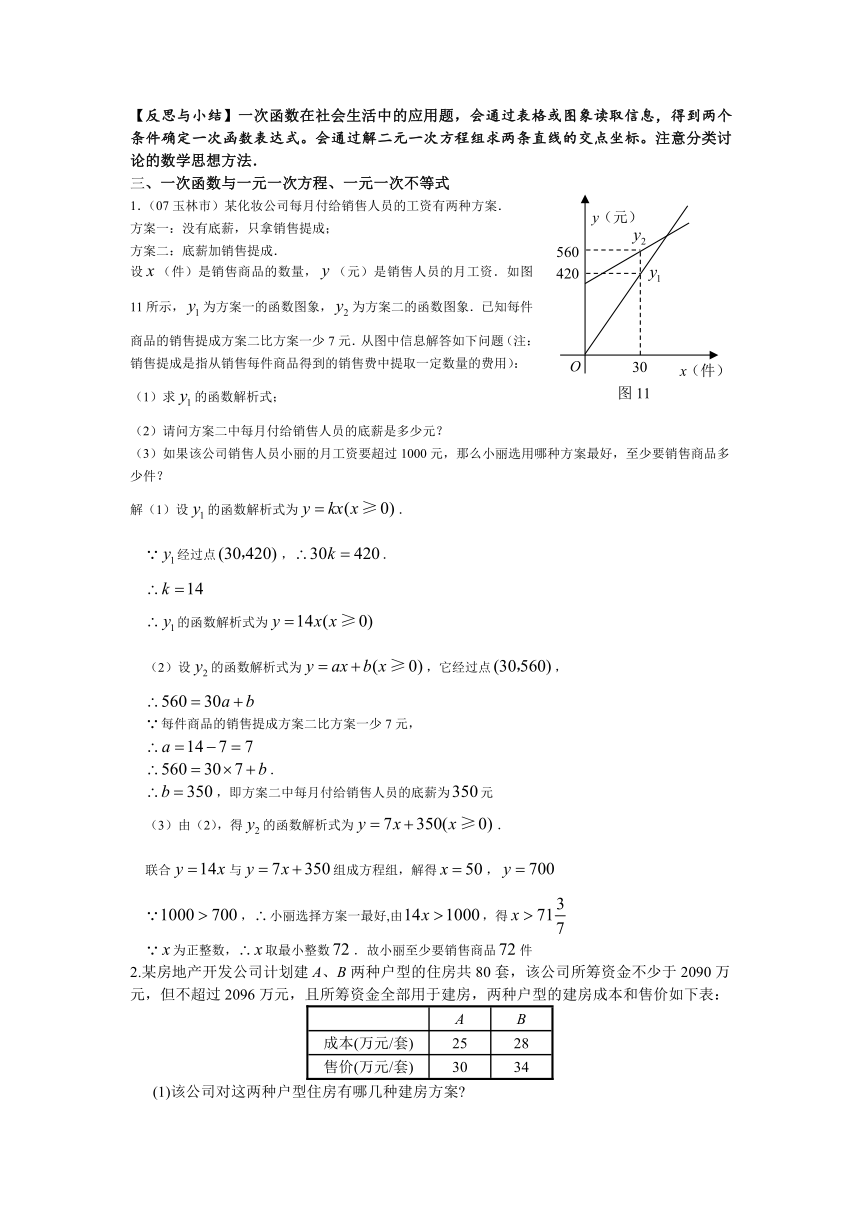
设（件）是销售商品的数量，（元）是销售人员的月工资．如图11所示，为方案一的函数图象，为方案二的函数图象．已知每件商品的销售提成方案二比方案一少7元．从图中信息解答如下问题（注：销售提成是指从销售每件商品得到的销售费中提取一定数量的费用）：
（1）求的函数解析式；
（2）请问方案二中每月付给销售人员的底薪是多少元？
（3）如果该公司销售人员小丽的月工资要超过1000元，那么小丽选用哪种方案最好，至少要销售商品多少件？
解（1）设的函数解析式为．
经过点，．
的函数解析式为
（2）设的函数解析式为，它经过点，
每件商品的销售提成方案二比方案一少7元，
．
，即方案二中每月付给销售人员的底薪为元
（3）由（2），得的函数解析式为．
联合与组成方程组，解得，
，小丽选择方案一最好,由，得
为正整数，取最小整数．故小丽至少要销售商品件
2.某房地产开发公司计划建A、B两种户型的住房共80套，该公司所筹资金不少于2090万元，但不超过2096万元，且所筹资金全部用于建房，两种户型的建房成本和售价如下表：
A B
成本(万元/套) 25 28
售价(万元/套) 30 34
(1)该公司对这两种户型住房有哪几种建房方案
(2)该公司如何建房获得利润最大
(3)根据市场调查，每套B型住房的售价不会改变，每套A型住房的售价将会提高a万元(a>0)，且所建的两种住房可全部售出，该公司又将如何建房获得利润最大
解析：(1)设A种户型的住房建x套，则B种户型的住房建(80-x)套．
由题意知2090≤25x+28(80-x)≤2096 48≤x≤50
∵ x取非负整数， ∴ x为48，49，50． ∴ 有三种建房方案：
A型48套，B型32套；A型49套，B型31套；A型50套，B型30套
(2)设该公司建房获得利润W(万元)． 由题意知W=5x+6(80-x)=480-x
∴ 当x=48时，W最大=432(万元) 即A型住房48套，B型住房32套获得利润最大
(3)由题意知W=(5+a)x+6(80-x)=480+(a-1)x ∴ 当O即A型住房建48套，B型住房建32套 当a=l时，a-1=0，三种建房方案获得利润相等
当a>1时，x=50，W最大，即A型住房建50套，B型住房建30套.
3. （2005沈阳）为实现沈阳森林城市建设的目标，今年春的绿化工作中，绿化办计划为某住宅小区购买并种植400株树苗，某树苗公司提供如下信息：
信息一：可供选择的树苗有杨树、丁香树、柳树、三种，并且要求购买杨树、丁香树的数量相等．
信息二：如下表：设购买杨树、柳树分别为x株，y株．
每株树苗批发价格（元） 两年后每株树苗对空气的净化指数
杨树 3 0.4
丁香树 2 0.1
柳树 P 0.2
（1） 写出y与x之间的函数关系式（不含自变量取值范围）
（2） 当每柳树的批发价P等于3元时，要使400株树苗两年后对该住宅小区的空气净化指数不低于90，应怎样安排这三种树苗的购买数量，才能使购买树苗的总费用最低？最低的总费用是多少元？
解：（1）由题意得
（2）根据题意得
解得设购买树苗的总费用为w元，则w=1200一x，故当x=200时，w最小，即当购买200株杨树、200株丁香树、不购买柳树苗时，能使购买树苗的总费用最低，最低的总费用是1000元．
【反思与小结】（1）解一元一次方程可以转化为：当函数值确定时，求与之对应的自变量的值。从图象上看，这相当于已知纵坐标确定横坐标的值。
（2）一元一次不等式ax+b>0或ax+b<0（a≠0）是一次函数y=ax+b（a≠0）的函数值不等于0的情形．
（3）直线y=ax+b上使函数值y>0（x轴上方的图像）的x的取值范围是ax+b＞0的解集；使函数值y<0（x轴下方的图像）的x的取值范围是ax+b＜0的解集．
四、分段函数
1．心理学家研究发现，一般情况下，学生的注意力随着教师讲课时间的变化而变化，讲课开始时，学生的注意力逐步增强，中间有一段时间学生的注意力保持较为理想的状态，随后学生的注意力开始分散，经过实验分析可知，学生的注意力y随时间t的变化规律有如下关系式：
（1）讲课开始后第5分钟时与讲课开始后第25分钟时比较，何时学生的注意力更集中？
（2）一道数学难题，需要讲解24分钟，为了效果较好，要求学生的注意力最低达到180，那么经过适当安排，老师能否在学生注意力达到所需的状态下讲解完这道题目？
解：（1）当x=5时，代入y=－t2+24t+100中，得y=195；当x=25时，代入y=－7t+24t+100中，得y=205．∴讲课开始后第25分钟时学生的注意力比讲课开始后第5分钟时更集中．
（2）当0＜t≤10时，令y=－t2+24t+100=180，得t=4；当10＜t≤20时，y=240；当20＜t≤40时，y=－7t+380=180，得t=28.57．
所以学生注意力在180以上的持续时间为28.57-4=24.57（分钟）．
∴老师可以经过适当安排，能在学生注意力达到所需的状态下讲解完这道题目．
2．参加保险公司的医疗保险，住院治疗的病人享受分段报销，保险公司制定的报销细则如下表.某人住院治疗后得到保险公司报销金额是1000元，那么此人住院的医疗费是___________．
住院医疗费（元） 报销率（%）
不超过500元的部分 0
超过500～1000元的部分 60
超过1000～3000元的部分 80
……
解：设住院医疗费为x（元），保险公司报销金额为y（元），根据表格有函数关系式：
y1=0（x≤500）；y2=（x-500）×60%=0.6x-300（500≤x≤1000），并且0≤y2≤300；
y3=（x-1000）×80%+500×60%=0.8x-500（1000≤x≤3000）并且 300≤y3≤1900…．
因y=1000（元），故应代入函数y3=0.8x-500中求解，所以当y=1000时，得x=1875．
即此人住院的医疗费是1875元．
3．荆州古城是闻名遐迩的历史文化名城．若“五一”黄金周有甲，乙两个旅行团到该景点参观，两团人数之和为120人，乙团不超过50人，设两团分别购票共付W元，甲团人数人，①求W与的函数关系式；②若甲团人数不超过100人，请说明两团合起来购票比分开购票最多可节约多少元？
解：（1）∵乙团不超过50人 ∴ 0＜120-x≤50 解得70≤x＜120，根据图象信息得，
当70≤x≤100时，W=6x+8（120-x）即，W=-2x+960（70≤x≤100）
当100＜x＜120时，W=4x+8（120-x）即，W=-4x+960（100＜x＜120）
（2）∵甲团人数不超过100人，∴ 70≤x≤100
即W与x函数关系式为W=-2x+960（70≤x≤100）
根据一次函数性质得，
当x=70时，W最大值=-2×70+960=820（元）
两团合起来购票应付款4×120=480（元）
所以两团合起来购票比分开购票最多可节约：
820-480=340（元）
【反思与小结】分段函数在近两年中考数学试题占有相当大的比例，能读懂分段函数表达式，并会根据实际问题或图象列表达式，在应用分段函数时，应特别注意自变量的取值范围。
【一试身手】
1. 如果点P(a,b)关于x轴的对称点p,在第三象限,那么直线y=ax+b的图像不经过 ( )
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
2.直线与轴交于点(－4 , 0)，则> 0时，的取值范围是 ( A )
A、>－4 B、>0 C、<－4 D、<0
3.已知一次函数y=x+m和y=-x+n的图像都经过点A(-2,0), 且与y轴分别交于B,C两点,那么△ABC的面积是 ( )
A. 2 B. 3 C. 4 D. 6
4.已知点A(-4, a),B(-2,b)都在一次函数y=x+k(k为常数)的图像上,则a与b的大小关系是a____b(填”<””=”或”>”);若k=2,则ab=___________.
5.根据一次函数y=-3x-6的图像,当函数值大于零时,x的范围是______________.
6.已知y-3与4x-2成正比例,且当x=1时,y=5.
(1) 求y与x的函数关系式;
(2) 求当x=-2时的函数值;
(3) 如果y的取值范围是0≤y≤5,求x的取值范围.
【提高训练】
1. 已知正比例函数y=(2m-1)x的图像上两点A(x1,y1),B(x2,y2),当x1y2,那么m的取值范围是 ( )
A. m< B. m> C. m<2 D. m>0
2. 一次函数y=2x+b与两坐标轴围成三角形的面积为4,则b=________________.
3. 已知一次函数y=2x-a与y=3x-b的图像交于x轴上原点外的一点,则=________.
4.若一次函数的图像于y轴分别交于点P和点Q，若点P与点Q关于x轴对称，则m= 。
5. (2007甘肃陇南) 如图，两摞相同规格的饭碗整齐地叠放在桌面上，请根据图中给的数据信息，解答下列问题：
（1）求整齐摆放在桌面上饭碗的高度y（cm）与饭碗数x（个）之间的一次函数解析式；
（2）把这两摞饭碗整齐地摆成一摞时，这摞饭碗的高度是多少？
解：（1）设．
由图可知：当时，；当时，．
把它们分别代入上式，得 ，
解得，．∴ 一次函数的解析式是．
(2)当时，．
即把这两摞饭碗整齐地摆成一摞时，这摞饭碗的高度是21cm．
6、（06安徽）15．如图①是公交公司某条公交线路的收支差额（即票价总收入减去运营成本）与乘客量之间的函数图象．目前这条线路亏损，为了扭亏，有关部门举行提高票价的听证会．
　　乘客代表认为：公交公司应改善管理，降低运营成本，以此举实现扭亏．
　　公交公司认为：运营成本难以下降，公司已尽力，应适当提高票价才能扭亏．
根据这两种意见，可以把图①分别改画成图②和图③．
（1）说明图①中点，点的实际意义．
（2）你认为图②和图③两个图象中，反映乘客意见的是图 ，反映公司意见的是图 ．
（3）如果公交公司采用适当提高票价，又减少成本的办法实现扭亏为赢，请你在图④中画出符合这种办法的与大致函数的图象．
解：（1）点表示公交公司的该条公交路线的运营成本为1万元．
点表示当乘客量为1.5万人时，公交公司的该条公交路线收支
恰好平衡．（2）图③；图②；
（3）把原射线略往上平移，再按逆时针旋转一个适当的角度
即可得到，如图所示．（若点沿轴平移至轴及轴上方不给分）
一次函数成就测试
班级 姓名 得分
一、用心填一填（每空10分，满分30分）．
1、（2007广西南宁）随着海拔高度的升高，大气压强下降，空气中的含氧量也随之下降，即含氧量与大气压强成正比例函数关系．
当时，，请写出与的函数关系式
2、已知直线与直线y=2+1的交点的横坐标为2，与直线y=－－8的交点的纵坐标为－7，则此直线的解析式是 。
3、（2007湖北孝感）如图，一次函数的图象经过A、B两点，则关于x的不等式的解集是 x<2
二、精心选一选（每小题10分，共30分）
1. 一次函数的图像交x轴于(2,0),交y轴于(0,3),当函数值大于0时,x的取值范围是 ( )
A. x>2 B. x<2 C. x>3 D. x<3
2、在同一坐标系中，直线y=(k－2)x+k和直线y=kx的位置可能是（ D ）
3、已知直线y=kx+b（k≠0）与x轴的交点在x轴的正半轴，下列结论（1）k＞0
b＞0 ；(2) k＞0 b＜0； (3) k＜0 b＞0； (4) k＜0 b＜0。 其中正确的有（ B ）
A、 1个 B、 2个 C、 3个 D、 4个
三、计算题（ 每小题20分，共40分）
1．（06南宁）第三届南宁国际龙舟赛于2006年6月3日至4日在南湖举行，甲、乙两队在比赛时，路程（米）与时间（分钟）的函数图象如图9所示，根据函数图象填空和解答问题：
（1）最先到达终点的是 队，比另一队领先 分钟到达；
（2）在比赛过程中，乙队在 分钟和 分钟时两次加速，图中点的坐标是 ，点的坐标是 ．
（3）假设乙队在第一次加速后，始终保持这个速度继续前进，那么甲、乙两队谁先到达终点？请说明理由．
解：（1）乙，；（2），，（每空1分，共6分）
　 （3）解：设所在直线表达式为
　　　　依题意　　　　解得
　　　　　　　　当米时，
　　　　（分钟）（或当时，米）
　　　　甲、乙两队同时到达终点
乙
甲
图11
图象与信息
（第3题图）
（万元）
Ａ
（万人）
Ｏ
Ｂ
图③
1
Ｂ
Ｏ
（万人）
Ａ
（万元）
图②
Ｂ
Ｏ
（万人）
Ａ
（万元）
图①
Ｂ
Ｏ
（万人）
Ａ
（万元）
Ｂ
Ｏ
（万人）
Ａ
（万元）
图④
O
30
560
420
人数(人)
6
图11
y（元）
x（件）
100
50
0
8
门票价格(元)
4