数学人教A版(2019)必修第一册5.2.1三角函数的概念 (第1课时) 课件(共20张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册5.2.1三角函数的概念 (第1课时) 课件(共20张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-25 20:54:23 | ||
图片预览





文档简介
(共20张PPT)
5.2任意角的三角函数
5.2.1 任意角的三角函数
第1课时
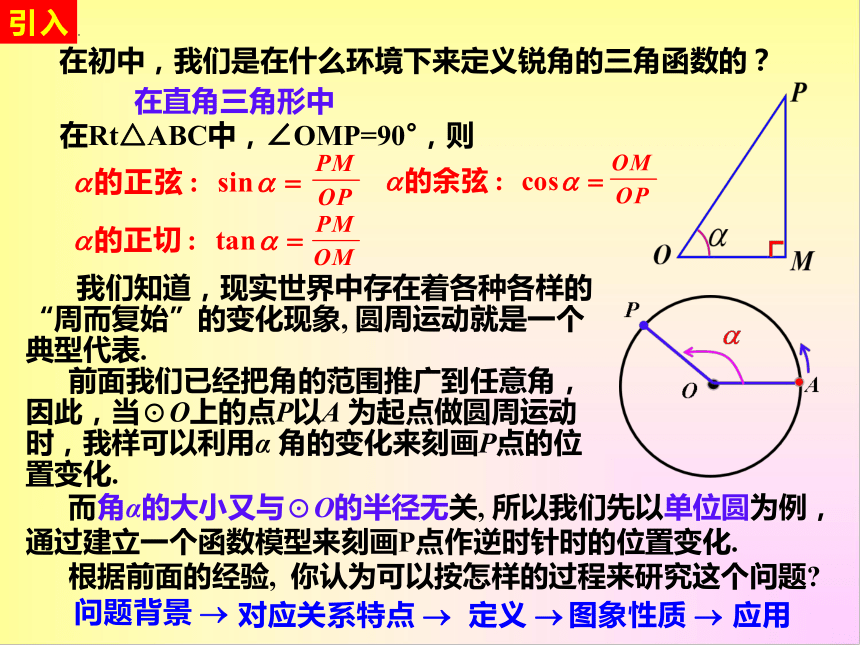
在初中,我们是在什么环境下来定义锐角的三角函数的?
引入
在直角三角形中
在Rt△ABC中,∠OMP=90°,则
我们知道,现实世界中存在着各种各样的“周而复始”的变化现象, 圆周运动就是一个典型代表.
前面我们已经把角的范围推广到任意角,因此,当⊙O上的点P以A 为起点做圆周运动时,我样可以利用α 角的变化来刻画P点的位置变化.
而角α的大小又与⊙O的半径无关, 所以我们先以单位圆为例,通过建立一个函数模型来刻画P点作逆时针时的位置变化.
根据前面的经验, 你认为可以按怎样的过程来研究这个问题
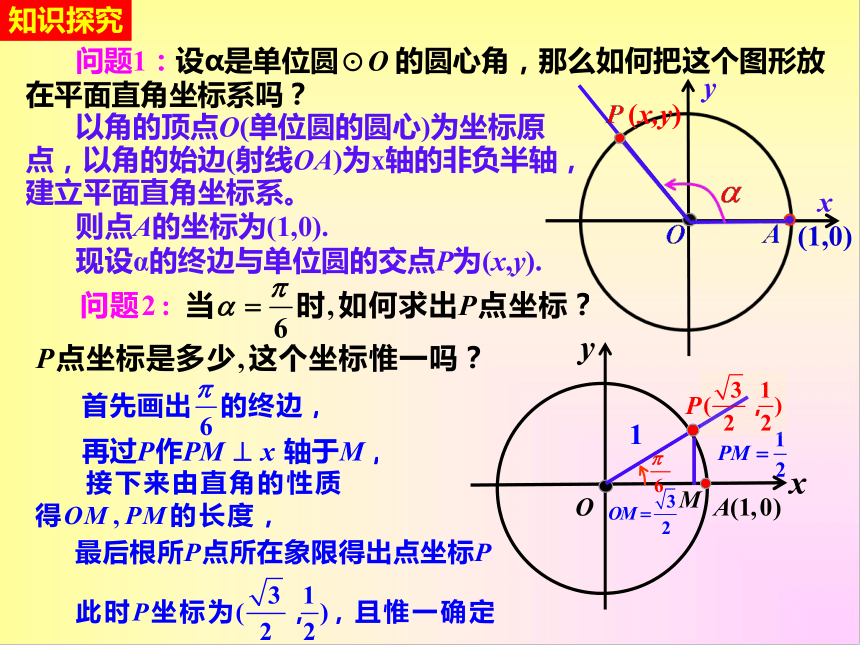
问题1:设α是单位圆⊙O 的圆心角,那么如何把这个图形放在平面直角坐标系吗?
知识探究
以角的顶点O(单位圆的圆心)为坐标原点,以角的始边(射线OA)为x轴的非负半轴,建立平面直角坐标系。
则点A的坐标为(1,0).
现设α的终边与单位圆的交点P为(x,y).
y
x
(1,0)
y
x
(x,y)
y
x
(1,0)
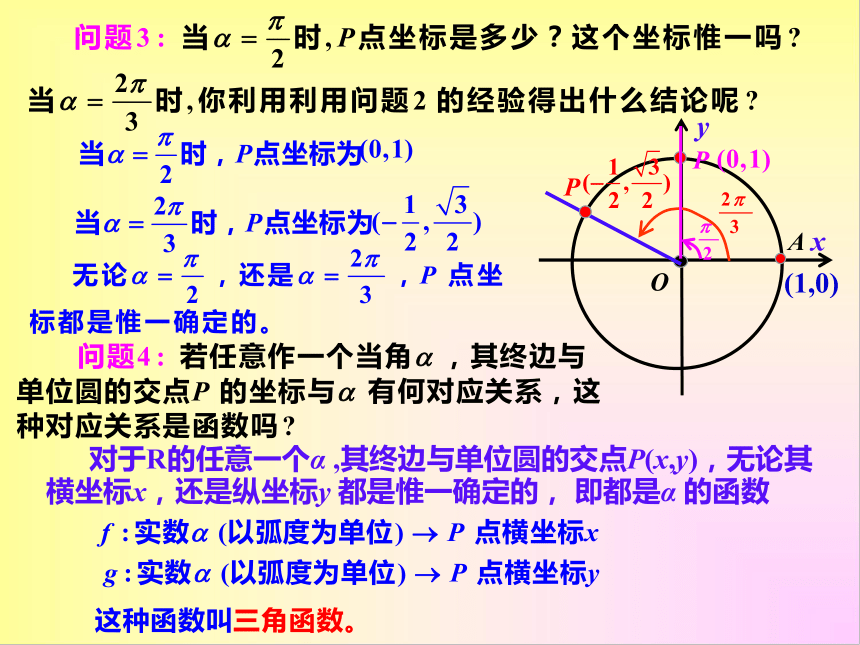
对于R的任意一个α ,其终边与单位圆的交点P(x,y),无论其横坐标x,还是纵坐标y 都是惟一确定的, 即都是α 的函数
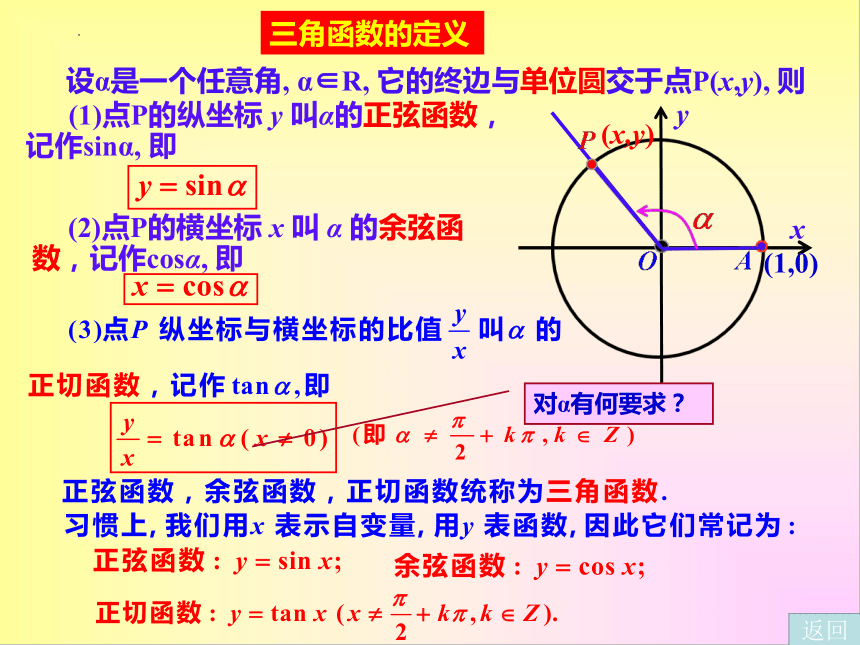
设α是一个任意角, α∈R, 它的终边与单位圆交于点P(x,y), 则
三角函数的定义
y
x
(1,0)
(x,y)
(1)点P的纵坐标 y 叫α的正弦函数,记作sinα, 即
(2)点P的横坐标 x 叫 α 的余弦函数,记作cosα, 即
对α有何要求?
返回
正弦函数y=sinx 余弦函数y=cosx 正切函数y=tanx
定义域
对应 关系
值域
三角函数的三要素
返回
y
x
如图,将Rt△POM平面直角坐标系,使点O与坐标原点重合,OM在经x轴的非负半轴上.
若射线OP与单位圆的交点为Q,
即现在的任意角三角函数与锐角三角函数的定义是相容的
作NQ⊥x轴于N
则点Q的横纵、坐标分别为
解:
例 析
解:
练习
轴线角的三角函数值
(教材P179练习第1 , 2题)
解:
解:
例析
设α 是一个任意角,P(x,y)是终边上的任意一点(除顶点外).
则点P与原点O的距离为
三角函数的定义
建系
画终边
取点
求比值
α 的三角函数只与终边的位置有关,与它终边上取点的位置无关。
所以,用单位圆上的点来定义并不失一般性,但更简单.
返回
解:
例析
由已知可得
1.已知角θ的终边过点 P(-12,5),求θ的三角函数值.
解:
练习
由已知可得
2.已知点P在半径为2的圆上沿顺时针方向做匀速圆周运动,角速度为1rad/s,求2s时点P的位置.
解:
设位置A为点P的起点.
∵点P的角速度为顺时针 1rad/s,
∴2s 时OP 转过的角α = -2rad/s.
现以圆心O 为坐标原点,射线 OA为x 轴的非负半轴建立直角坐标系。则
(教材P180练习第3,4题)
(教材P182练习第1题)
2.说说三角函数的定义
小 结
这两个定义等价吗 它与锐角三角函数相容吗?
1.说说三角函数概念的抽象过程,它与幂、指、对函数的对应关系有何异同?
3.根据定义求一个角三角函数的过程是怎样的?
定义1
定义2
1.教材P184习题5.2第1(1)(2),3题(要求:第1题只用定义法).
作 业
再 见
5.2任意角的三角函数
5.2.1 任意角的三角函数
第1课时
在初中,我们是在什么环境下来定义锐角的三角函数的?
引入
在直角三角形中
在Rt△ABC中,∠OMP=90°,则
我们知道,现实世界中存在着各种各样的“周而复始”的变化现象, 圆周运动就是一个典型代表.
前面我们已经把角的范围推广到任意角,因此,当⊙O上的点P以A 为起点做圆周运动时,我样可以利用α 角的变化来刻画P点的位置变化.
而角α的大小又与⊙O的半径无关, 所以我们先以单位圆为例,通过建立一个函数模型来刻画P点作逆时针时的位置变化.
根据前面的经验, 你认为可以按怎样的过程来研究这个问题
问题1:设α是单位圆⊙O 的圆心角,那么如何把这个图形放在平面直角坐标系吗?
知识探究
以角的顶点O(单位圆的圆心)为坐标原点,以角的始边(射线OA)为x轴的非负半轴,建立平面直角坐标系。
则点A的坐标为(1,0).
现设α的终边与单位圆的交点P为(x,y).
y
x
(1,0)
y
x
(x,y)
y
x
(1,0)
对于R的任意一个α ,其终边与单位圆的交点P(x,y),无论其横坐标x,还是纵坐标y 都是惟一确定的, 即都是α 的函数
设α是一个任意角, α∈R, 它的终边与单位圆交于点P(x,y), 则
三角函数的定义
y
x
(1,0)
(x,y)
(1)点P的纵坐标 y 叫α的正弦函数,记作sinα, 即
(2)点P的横坐标 x 叫 α 的余弦函数,记作cosα, 即
对α有何要求?
返回
正弦函数y=sinx 余弦函数y=cosx 正切函数y=tanx
定义域
对应 关系
值域
三角函数的三要素
返回
y
x
如图,将Rt△POM平面直角坐标系,使点O与坐标原点重合,OM在经x轴的非负半轴上.
若射线OP与单位圆的交点为Q,
即现在的任意角三角函数与锐角三角函数的定义是相容的
作NQ⊥x轴于N
则点Q的横纵、坐标分别为
解:
例 析
解:
练习
轴线角的三角函数值
(教材P179练习第1 , 2题)
解:
解:
例析
设α 是一个任意角,P(x,y)是终边上的任意一点(除顶点外).
则点P与原点O的距离为
三角函数的定义
建系
画终边
取点
求比值
α 的三角函数只与终边的位置有关,与它终边上取点的位置无关。
所以,用单位圆上的点来定义并不失一般性,但更简单.
返回
解:
例析
由已知可得
1.已知角θ的终边过点 P(-12,5),求θ的三角函数值.
解:
练习
由已知可得
2.已知点P在半径为2的圆上沿顺时针方向做匀速圆周运动,角速度为1rad/s,求2s时点P的位置.
解:
设位置A为点P的起点.
∵点P的角速度为顺时针 1rad/s,
∴2s 时OP 转过的角α = -2rad/s.
现以圆心O 为坐标原点,射线 OA为x 轴的非负半轴建立直角坐标系。则
(教材P180练习第3,4题)
(教材P182练习第1题)
2.说说三角函数的定义
小 结
这两个定义等价吗 它与锐角三角函数相容吗?
1.说说三角函数概念的抽象过程,它与幂、指、对函数的对应关系有何异同?
3.根据定义求一个角三角函数的过程是怎样的?
定义1
定义2
1.教材P184习题5.2第1(1)(2),3题(要求:第1题只用定义法).
作 业
再 见
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
