湖北省武汉市新洲区部分学校2023-2024学年高二上学期期中质量检测数学试题(含答案)
文档属性
| 名称 | 湖北省武汉市新洲区部分学校2023-2024学年高二上学期期中质量检测数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 823.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-25 21:19:15 | ||
图片预览




文档简介
武汉市新洲区部分学校2023-2024学年高二上学期期中质量检测
数学试题
考试用时:120分钟 满分:150分 2023.11
第Ⅰ卷(选择题 共60分)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.从长度为1,3,5,7,9的5根木棒中任选3根,能构成三角形的概率为( )
A. B. C. D.
2.已知向量,,若,则实数等于( )
A. B. C.0 D.1
3.直线的倾斜角为( )
A. B. C. D.
4.设,则“”是“直线与直线平行”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
5.求经过点,且以为圆心的圆的一般方程( )
A. B.
C. D.
6.椭圆:左右焦点分别为、,焦距为2,直线经过交椭圆于,两点,若的周长为12,则椭圆标准方程为( )
A. B. C. D.
7.若圆上总存在两点到原点的距离为1,则实数的取值范围是( )
A. B. C. D.
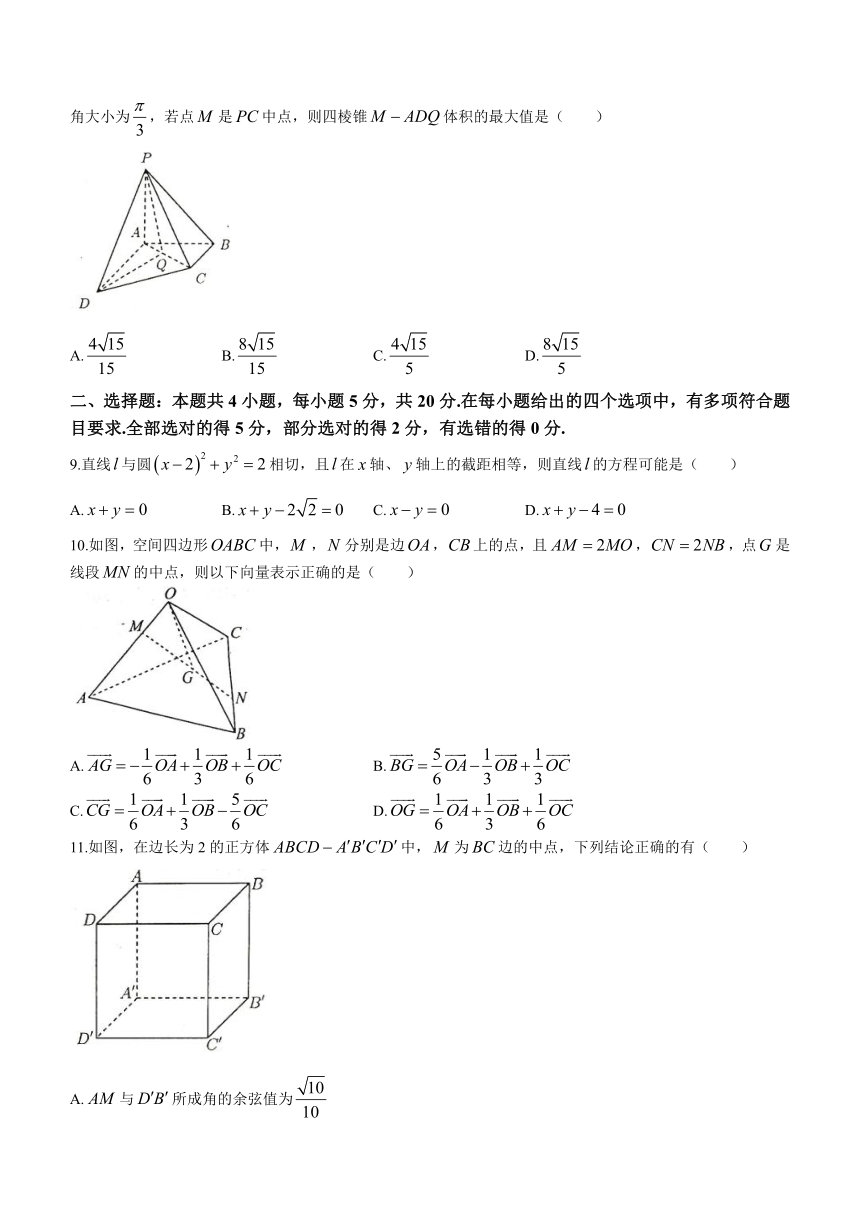
8.如图,在四棱锥中,已知:平面,,,,已知是四边形内部一点(包括边界),且二面角的平面角大小为,若点是中点,则四棱锥体积的最大值是( )
A. B. C. D.
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.直线与圆相切,且在轴、轴上的截距相等,则直线的方程可能是( )
A. B. C. D.
10.如图,空间四边形中,,分别是边,上的点,且,,点是线段的中点,则以下向量表示正确的是( )
A. B.
C. D.
11.如图,在边长为2的正方体中,为边的中点,下列结论正确的有( )
A.与所成角的余弦值为
B.过,,三点的正方体的截面面积为9
C.当在线段上运动时,三棱锥的体积恒为定值
D.若为正方体表面上的一个动点,,分别为的三等分点,则的最小值为
12.法国著名数学家加斯帕尔·蒙日在研究圆锥曲线时发现:椭圆的任意两条互相垂直的切线的交点的轨迹是以坐标原点为圆心,为半径的圆,这个圆称为蒙日圆.若矩形的四边均与椭圆相切,则下列说法正确的是( )
A.椭圆的蒙日圆方程为
B.若为正方形,则的边长为
C.若是椭圆蒙日圆上一个动点,过作椭圆的两条切线,与该蒙日圆分别交于,两点,则面积的最大值为18
D.若是直线:上的一点,过点作椭圆的两条切线与椭圆相切于,两点,是坐标原点,连接,当为直角时,或
第Ⅱ卷(非选择题 共90分)
三、填空题:本题共4小题,每小题5分,共20分
13.某公司的入职面试中有3道难度相当的题目,王宁答对每道题目的概率都是0.6,若每位面试者共有3次机会,一旦某次答对抽到的题目,则面试通过,否则就一直抽题到第3次为止.假设对抽到的不同题目能否答对是独立的,那么王宁最终通过面试的概率是________.
14.已知点,直线与圆:交于两点,若为等腰直角三角形,则直线的方程为________.(写出一条即可)
15.如图,正方形和的边长都是1,且平面,点、分别在、上移动,若,则线段长度的最小值为________.
16.已知椭圆的左、右焦点分别为,,为坐标原点,点在椭圆上,且,则________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分10分)
一个袋子中有4个红球,6个黄球,采用不放回方式从中依次随机地取出2个球.
(1)求第二次取到黄球的概率;
(2)求两次取到的球颜色相同的概率.
18.(本小题满分12分)
已知直线:和圆:.
(1)求与直线垂直且经过圆心的直线方程;
(2)求与直线平行且与圆相切的直线方程.
19.(本小题满分12分)
已知空间中三点,,.设,.
(1)求和;
(2)若与互相垂直,求实数的值.
20.(本小题满分12分)
已知圆:,点是直线:上的一动点,过点作圆的切线,,切点为,.
(1)当切线的长度为时,求点的坐标;
(2)求线段长度的最小值.
21.(本小题满分12分)
如图,已知四棱锥的底面是菱形,,为边的中点,,,.
(1)证明:;
(2)试判断线段上是否存在点使得二面角的余弦值为,若存在求出点的位置;若不存在,请说明理由.
22.(本小题满分12分)
如图所示,椭圆的上顶点和右顶点分别是和,离心率,,是椭圆上的两个动点,且.
(1)求椭圆的标准方程;
(2)求四边形面积的最大值;
(3)试判断直线与的斜率之积是否为定值,若是,求出定值;若不是,请说明理由.
武汉市新洲区部分学校2023-2024学年高二上学期期中质量检测
答案
一、单项选择题:
1.A 2.D 3.C 4.A 5.B 6.D 7.C 8.B
二、多项选择题:
9.ACD 10.CD 11.AC 12.ABD
三、填空题:
13.0.936 14.(或或) 15. 16.1
四、解答题:
17.解:(1)从10个球中不放回的随机取出2个球共有(种)可能,即.记事件“两次取出的都是红球”,则;记事件“第一次取出红球,第二次取出黄球”,则;记事件“第一次取出黄球,第二次取出红球”,则;记事件“两次取出的都是黄球”,则;事件,,,两两互斥.故(第二次取到黄球);
(2)(两次取到的球颜色相同)
18.解:(1)设与直线垂直的直线为
圆可化为,圆心为,又因为直线经过圆心,所以,即
故所求直线方程为.
(2)设与直线平行的直线为.
又因为直线与圆相切,所以圆心到直线的距离等于半径,即,所以,或5
故所求直线方程为或.
19.解:(1)∵,,,,.
∴,
于是
.
(2)∵,
又与互相垂直
∴
即
∴,
20.解:(1)由题可知,圆的半径,设,
因为是圆的一条切线,所以,
所以,
解得或
所以点的坐标为或.
(2)设,因为,是圆的两条切线,所以,
所以,,,四点共圆,且以为直径,设圆心为,则其方程为
,
即①
又圆②
①-②得圆与圆相交弦所在直线方程为
.
点到直线的距离,
所以相交弦长
,所以当时,有最小值.
21.解:(1)连接,因为,所以,
因为底面是菱形,,所以,因为为边的中点,所以
∴
因为,
所以
因此,即,
又因为,所以,
又,平面,平面,所以平面,又平面,所以,即
(2)由(1)知,,两两垂直,故以为坐标原点,,,为,,轴建立如图示空间直角坐标系,则,,,,,于是
,,令,
则
取平面的一个法向量为,设平面的一个法向量为,
因为,所以
又二面角为锐二面角且设为,所以
,
即,(负值舍去),
故存在点使得二面角的余弦值
为,此时点满足.
22.解:(1)因为,所以,又离心率为,所以,即,,所以椭圆的标准方程为
(2)因为,所以,所以,设直线的方程为,,,由得,
由得,又,
,
直线方程为,所以,
又直线与之间的距离为,故四边形的面积,令,则,令,则,所以,所以当时,即时,四边形面积的最大值为4
(3)由第(2)问得,,
,
故直线与的斜率之积为定值,且定值为.
数学试题
考试用时:120分钟 满分:150分 2023.11
第Ⅰ卷(选择题 共60分)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.从长度为1,3,5,7,9的5根木棒中任选3根,能构成三角形的概率为( )
A. B. C. D.
2.已知向量,,若,则实数等于( )
A. B. C.0 D.1
3.直线的倾斜角为( )
A. B. C. D.
4.设,则“”是“直线与直线平行”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
5.求经过点,且以为圆心的圆的一般方程( )
A. B.
C. D.
6.椭圆:左右焦点分别为、,焦距为2,直线经过交椭圆于,两点,若的周长为12,则椭圆标准方程为( )
A. B. C. D.
7.若圆上总存在两点到原点的距离为1,则实数的取值范围是( )
A. B. C. D.
8.如图,在四棱锥中,已知:平面,,,,已知是四边形内部一点(包括边界),且二面角的平面角大小为,若点是中点,则四棱锥体积的最大值是( )
A. B. C. D.
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.直线与圆相切,且在轴、轴上的截距相等,则直线的方程可能是( )
A. B. C. D.
10.如图,空间四边形中,,分别是边,上的点,且,,点是线段的中点,则以下向量表示正确的是( )
A. B.
C. D.
11.如图,在边长为2的正方体中,为边的中点,下列结论正确的有( )
A.与所成角的余弦值为
B.过,,三点的正方体的截面面积为9
C.当在线段上运动时,三棱锥的体积恒为定值
D.若为正方体表面上的一个动点,,分别为的三等分点,则的最小值为
12.法国著名数学家加斯帕尔·蒙日在研究圆锥曲线时发现:椭圆的任意两条互相垂直的切线的交点的轨迹是以坐标原点为圆心,为半径的圆,这个圆称为蒙日圆.若矩形的四边均与椭圆相切,则下列说法正确的是( )
A.椭圆的蒙日圆方程为
B.若为正方形,则的边长为
C.若是椭圆蒙日圆上一个动点,过作椭圆的两条切线,与该蒙日圆分别交于,两点,则面积的最大值为18
D.若是直线:上的一点,过点作椭圆的两条切线与椭圆相切于,两点,是坐标原点,连接,当为直角时,或
第Ⅱ卷(非选择题 共90分)
三、填空题:本题共4小题,每小题5分,共20分
13.某公司的入职面试中有3道难度相当的题目,王宁答对每道题目的概率都是0.6,若每位面试者共有3次机会,一旦某次答对抽到的题目,则面试通过,否则就一直抽题到第3次为止.假设对抽到的不同题目能否答对是独立的,那么王宁最终通过面试的概率是________.
14.已知点,直线与圆:交于两点,若为等腰直角三角形,则直线的方程为________.(写出一条即可)
15.如图,正方形和的边长都是1,且平面,点、分别在、上移动,若,则线段长度的最小值为________.
16.已知椭圆的左、右焦点分别为,,为坐标原点,点在椭圆上,且,则________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分10分)
一个袋子中有4个红球,6个黄球,采用不放回方式从中依次随机地取出2个球.
(1)求第二次取到黄球的概率;
(2)求两次取到的球颜色相同的概率.
18.(本小题满分12分)
已知直线:和圆:.
(1)求与直线垂直且经过圆心的直线方程;
(2)求与直线平行且与圆相切的直线方程.
19.(本小题满分12分)
已知空间中三点,,.设,.
(1)求和;
(2)若与互相垂直,求实数的值.
20.(本小题满分12分)
已知圆:,点是直线:上的一动点,过点作圆的切线,,切点为,.
(1)当切线的长度为时,求点的坐标;
(2)求线段长度的最小值.
21.(本小题满分12分)
如图,已知四棱锥的底面是菱形,,为边的中点,,,.
(1)证明:;
(2)试判断线段上是否存在点使得二面角的余弦值为,若存在求出点的位置;若不存在,请说明理由.
22.(本小题满分12分)
如图所示,椭圆的上顶点和右顶点分别是和,离心率,,是椭圆上的两个动点,且.
(1)求椭圆的标准方程;
(2)求四边形面积的最大值;
(3)试判断直线与的斜率之积是否为定值,若是,求出定值;若不是,请说明理由.
武汉市新洲区部分学校2023-2024学年高二上学期期中质量检测
答案
一、单项选择题:
1.A 2.D 3.C 4.A 5.B 6.D 7.C 8.B
二、多项选择题:
9.ACD 10.CD 11.AC 12.ABD
三、填空题:
13.0.936 14.(或或) 15. 16.1
四、解答题:
17.解:(1)从10个球中不放回的随机取出2个球共有(种)可能,即.记事件“两次取出的都是红球”,则;记事件“第一次取出红球,第二次取出黄球”,则;记事件“第一次取出黄球,第二次取出红球”,则;记事件“两次取出的都是黄球”,则;事件,,,两两互斥.故(第二次取到黄球);
(2)(两次取到的球颜色相同)
18.解:(1)设与直线垂直的直线为
圆可化为,圆心为,又因为直线经过圆心,所以,即
故所求直线方程为.
(2)设与直线平行的直线为.
又因为直线与圆相切,所以圆心到直线的距离等于半径,即,所以,或5
故所求直线方程为或.
19.解:(1)∵,,,,.
∴,
于是
.
(2)∵,
又与互相垂直
∴
即
∴,
20.解:(1)由题可知,圆的半径,设,
因为是圆的一条切线,所以,
所以,
解得或
所以点的坐标为或.
(2)设,因为,是圆的两条切线,所以,
所以,,,四点共圆,且以为直径,设圆心为,则其方程为
,
即①
又圆②
①-②得圆与圆相交弦所在直线方程为
.
点到直线的距离,
所以相交弦长
,所以当时,有最小值.
21.解:(1)连接,因为,所以,
因为底面是菱形,,所以,因为为边的中点,所以
∴
因为,
所以
因此,即,
又因为,所以,
又,平面,平面,所以平面,又平面,所以,即
(2)由(1)知,,两两垂直,故以为坐标原点,,,为,,轴建立如图示空间直角坐标系,则,,,,,于是
,,令,
则
取平面的一个法向量为,设平面的一个法向量为,
因为,所以
又二面角为锐二面角且设为,所以
,
即,(负值舍去),
故存在点使得二面角的余弦值
为,此时点满足.
22.解:(1)因为,所以,又离心率为,所以,即,,所以椭圆的标准方程为
(2)因为,所以,所以,设直线的方程为,,,由得,
由得,又,
,
直线方程为,所以,
又直线与之间的距离为,故四边形的面积,令,则,令,则,所以,所以当时,即时,四边形面积的最大值为4
(3)由第(2)问得,,
,
故直线与的斜率之积为定值,且定值为.
同课章节目录
