北京市海淀区重点中学2023-2024学年高二上学期期中练习数学试题(含答案)
文档属性
| 名称 | 北京市海淀区重点中学2023-2024学年高二上学期期中练习数学试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 701.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-25 00:00:00 | ||
图片预览



文档简介
北京市海淀区重点中学2023-2024学年高二上学期期中练习
数学
2023年11月3日
说明:本试卷共六道大题,共7页,满分150分,考试时间120分钟
第I卷(共18题,满分100分)
一、选择题(本大题共10小题,每小题4分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确答案填涂在答题纸上的相应位置。)
1.已知平面平面,直线,直线,则a与b的位置关系是( )
A.平行 B.平行或异面 C.异面 D.异面或相交
2.空间中点A的坐标是,若向量,则点B的坐标是( )
A. B. C. D.
3.一个水平放置的平面图形用斜二测画法作出的直观图是如图所示的等腰直角,其中,则平面图形的面积为( )
A. B. C. D.
4.已知,则下列说法错误的是( )
A.若分别是直线的方向向量,则所成角余弦值是
B.若分别是直线l的方向向量与平面的法向量,则l与所成角正弦值是
C.若分别是平面ABC,平面BCD的法向量,则二面角的余弦值是
D.若分别是直线l的方向向量与平面的法向量,则l与所成角余弦值是
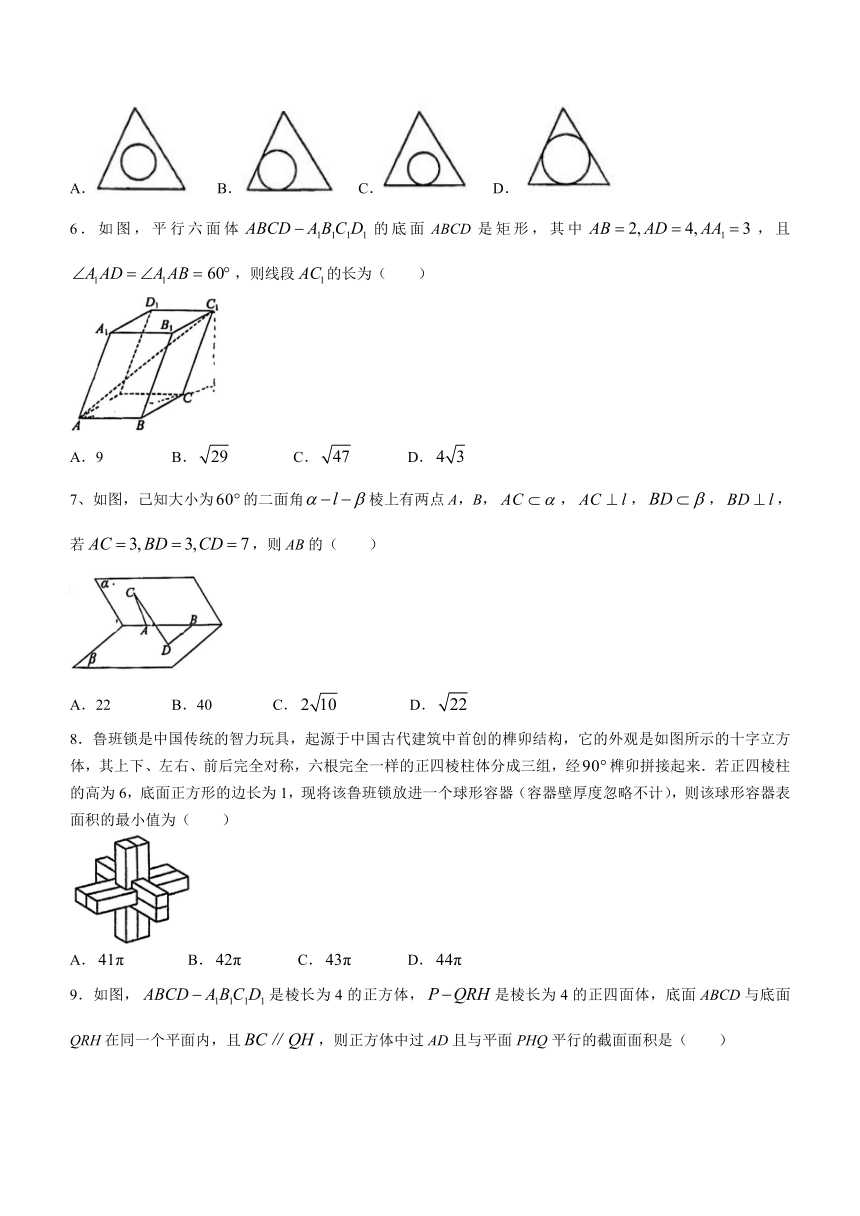
5.一个三棱锥的各棱长均相等,其内部有一个内切球,即球与三棱锥的各面均相切,过一条侧棱和其对边的中点作三棱锥的截面,所得截面图形是( )
A. B. C. D.
6.如图,平行六面体的底面ABCD是矩形,其中,且,则线段的长为( )
A.9 B. C. D.
7、如图,己知大小为的二面角棱上有两点A,B,,,,,若,则AB的( )
A.22 B.40 C. D.
8.鲁班锁是中国传统的智力玩具,起源于中国古代建筑中首创的榫卯结构,它的外观是如图所示的十字立方体,其上下、左右、前后完全对称,六根完全一样的正四棱柱体分成三组,经榫卯拼接起来.若正四棱柱的高为6,底面正方形的边长为1,现将该鲁班锁放进一个球形容器(容器壁厚度忽略不计),则该球形容器表面积的最小值为( )
A. B. C. D.
9.如图,是棱长为4的正方体,是棱长为4的正四面体,底面ABCD与底面QRH在同一个平面内,且,则正方体中过AD且与平面PHQ平行的截面面积是( )
A. B. C. D.
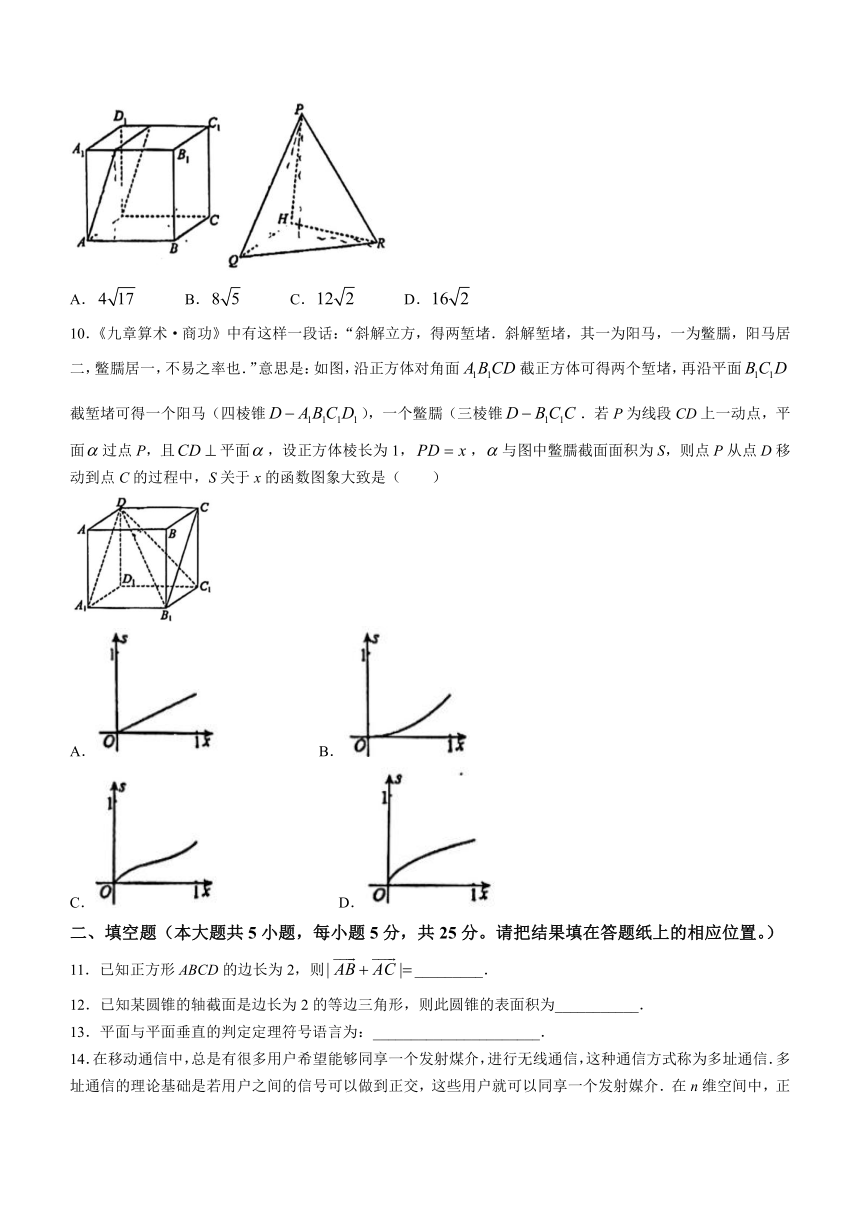
10.《九章算术·商功》中有这样一段话:“斜解立方,得两堑堵.斜解堑堵,其一为阳马,一为鳖臑,阳马居二,鳖臑居一,不易之率也.”意思是:如图,沿正方体对角面截正方体可得两个堑堵,再沿平面截堑堵可得一个阳马(四棱锥),一个鳖臑(三棱锥.若P为线段CD上一动点,平面过点P,且平面,设正方体棱长为1,,与图中鳖臑截面面积为S,则点P从点D移动到点C的过程中,S关于x的函数图象大致是( )
A. B.
C. D.
二、填空题(本大题共5小题,每小题5分,共25分。请把结果填在答题纸上的相应位置。)
11.已知正方形ABCD的边长为2,则_________.
12.已知某圆锥的轴截面是边长为2的等边三角形,则此圆锥的表面积为___________.
13.平面与平面垂直的判定定理符号语言为:______________________.
14.在移动通信中,总是有很多用户希望能够同享一个发射煤介,进行无线通信,这种通信方式称为多址通信.多址通信的理论基础是若用户之间的信号可以做到正交,这些用户就可以同享一个发射媒介.在n维空间中,正交的定义是两个n维向量满足.己知某通信方式中用户的信号是4维非零向量,有四个用户同享一个发射媒介,已知前三个用户的信号向量为,写出一个满足条件的第四个用户的信号向量____________.
15.一个三棱锥的三个侧面中有一个是边长为2的正三角形,另两个是等腰直角三角形,则该三棱锥的体积可能为___________.
三、解答题(本大题共3小题,共35分。解答应写出文字说明过程或演算步骤,请将答案写在答题纸上的相应位置。)
16.(本题10分)
已知空间直角坐标系中四个点的坐标分别为:,
(I)求;
(II)若,求x的值;
(Ⅲ)若D点在平面ABC上,直接写出x的值.
17.(本题12分)
如图所示,在四棱锥中,平面PAD,,E是PD的中点.
(I)求证:;
(II)求证:平面PAB;
(Ⅲ)若M是线段CE上一动点,则线段AD上是否存在点N,使平面PAB 并说明理由.
18.(本题13分)
如图所示,已知四棱锥中,ABCD是直角梯形,,平面平面ABCD,.
(I)证明:平面ABCD;
(I)求B到平面ADE的距离;
(Ⅲ)求二面角的余弦值.
第Ⅱ卷(共8道题,满分50分)
一、选择题(共4小题,每小题5分,共20分。在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确答案填涂在答题纸上的相应位置。)
19.关于空间中的角,下列说法中正确的个数是( )
①空间中两条直线所成角的取值范围是
②空间中直线与平面所成角的取值范围是
③空间中二面角的平面角的取值范围是
④空间中平面与平面所成角的取值范围是
A.1 B.2 C.3 D.4
20.如图,在正方形ABCD中,点E,F分别为边BC,AD的中点,将沿BF所在直线进行翻折,将沿DE所在直线进行翻折,在翻折的过程中,下列说法正确的是( )
A.点A与点C在某一位置可能重合 B.点A与点C的最大距离为
C.直线AB与直线DE可能垂直 D.直线AF与直线CE可能垂直
21.在正方体中,P为棱上一动点,Q为底面ABCD上一动点,M是线段PQ的中点,若点P,Q都运动时,点M构成的点集是一个空间几何体,则这个几何体是( )
A.棱柱 B.棱台 C.棱锥 D.球的一部分
22.如图,在棱长为2的正方体中,P为线段的中点,Q为线段上的动点,则下列结论正确的是( )
A.存在点Q,使得 B.存在点Q,使得PQ与AD所成的角为
C.三棱锥的体积是定值 D.存在点Q,使得平面
二、填空题(共3小题,每小题5分,共15分。把答案填在答题纸上的相应位置。)
23.如图,在边长为2正方体中,E为BC的中点,点P在正方体表面上移动,且满足,则点和满足条件的所有点P构成的图形的周长是___________.
24.已知正三棱柱的所有侧棱长及底面边长都为2,D是侧棱的中点,则直线AD与平面所成角的正弦值为___________.
25.点O是正四面体的外接球球心,.
若,其中,则动点P扫过的区域的体积为___________.
三、解答题(本小题15分,解答应写出文字说明过程或演算步骤。请将答案写在答题纸上的相应位置。)
26.己知自然数集,非空集合,若集合E满足:对任意,存在,使得,称集合E为集合A的一组m元基底.
(I)分别判断下列集合E是否为集合A的一组二元基底,并说明理由:
①;
②.
(II)若集合E是集合A的一组m元基底,证明:;
(III)若集合E为集合的一组m元基底,求m的最小值.
北京市海淀区重点中学2023-2024学年高二上学期期中练习
数学
参考答案及评分标准
I卷
一、选择题(共10小题,每小题4分,共40分。)
(1)B (2)C (3)B (4)C (5)B (6)C (7)C (8)A (9)C (10)B
二、填空题(共5小题,每小题5分,共25分。)
(11) (12)
(13)若,则
(14)(答案不唯一,即可)
(15)或或(仅看正确答案,答出1个2分,2个3分,答案全对5分)
三、解答题(共3小题,共35分。)
(16)(共10分)
解(I), 1分
3分
(II). 5分
因为,所以 6分
即,解得 7分
(III) 10分
(17)(共12分)
解:(I)因为平面PAD,在四棱锥中, 1分
平面ABCD, 2分
平面平面ABCD, 3分
所以
(II)取F为AP中点,连接EF,BF, 4分
因为E,F是PD,PA的中点.
所以且,
由(I)知,又.
所以四边形BCEF下为平行四边形, 5分
所以,
又平面PAB, 6分
平面PAB,
所以平面PAB 7分
(若用面面平行证明则对应给分;辅助线1分;两个平行各1分,两条相交直线1分)
(III)线段AD存在点N,使得平面PAB,理由如下: 8分
取AD中点N,连接CN,EN,
因为E,N分别为PD,AD的中点,所以,
因为平面PAB,
平面PAB,
所以平面PAB. 10分
由(II)知:平面PAB,
又平面CEN,
所以平面平面PAB,
又M是CE上的动点,平面CEN,
所以平面PAB,所以线段AD存在N,使得面PAB 12分
(18)(共13分)
解:(T)在四棱锥中,
,
因为,由勾股定理逆定理得 1分
又因为平面平面ABCD, 2分
平面平面, 3分
平面EAB, 4分
所以平面ABCD;
(II)由(I)得平面ABCD;
因为BA,平面ABCD,
所以,又,所以EB,BA,BC两两垂直,
以B为原点建立空间直角坐标系如图.
. 5分
设平面ADE的法向量,
,令,得 6分
设B到平面ADE距离为d,,
则 8分
几何法过B作AE的垂线段,直接求出高,
证明是垂线段的过程线面垂直2分,答案2分;
等积法,体积1分,底面积1分,答案2分.
(III)
设平面DEC的法向量,
令,得 10分
, 12分
设二面角为,由图可知为钝角,
故 13分
Ⅱ卷
一、选择题(共4小题,每小题5分,共20分)
(19)C (20)D (21)A (22)D
二、填空题(共3小题,每小题5分,共15分)
(23) (24) (25)
数学
2023年11月3日
说明:本试卷共六道大题,共7页,满分150分,考试时间120分钟
第I卷(共18题,满分100分)
一、选择题(本大题共10小题,每小题4分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确答案填涂在答题纸上的相应位置。)
1.已知平面平面,直线,直线,则a与b的位置关系是( )
A.平行 B.平行或异面 C.异面 D.异面或相交
2.空间中点A的坐标是,若向量,则点B的坐标是( )
A. B. C. D.
3.一个水平放置的平面图形用斜二测画法作出的直观图是如图所示的等腰直角,其中,则平面图形的面积为( )
A. B. C. D.
4.已知,则下列说法错误的是( )
A.若分别是直线的方向向量,则所成角余弦值是
B.若分别是直线l的方向向量与平面的法向量,则l与所成角正弦值是
C.若分别是平面ABC,平面BCD的法向量,则二面角的余弦值是
D.若分别是直线l的方向向量与平面的法向量,则l与所成角余弦值是
5.一个三棱锥的各棱长均相等,其内部有一个内切球,即球与三棱锥的各面均相切,过一条侧棱和其对边的中点作三棱锥的截面,所得截面图形是( )
A. B. C. D.
6.如图,平行六面体的底面ABCD是矩形,其中,且,则线段的长为( )
A.9 B. C. D.
7、如图,己知大小为的二面角棱上有两点A,B,,,,,若,则AB的( )
A.22 B.40 C. D.
8.鲁班锁是中国传统的智力玩具,起源于中国古代建筑中首创的榫卯结构,它的外观是如图所示的十字立方体,其上下、左右、前后完全对称,六根完全一样的正四棱柱体分成三组,经榫卯拼接起来.若正四棱柱的高为6,底面正方形的边长为1,现将该鲁班锁放进一个球形容器(容器壁厚度忽略不计),则该球形容器表面积的最小值为( )
A. B. C. D.
9.如图,是棱长为4的正方体,是棱长为4的正四面体,底面ABCD与底面QRH在同一个平面内,且,则正方体中过AD且与平面PHQ平行的截面面积是( )
A. B. C. D.
10.《九章算术·商功》中有这样一段话:“斜解立方,得两堑堵.斜解堑堵,其一为阳马,一为鳖臑,阳马居二,鳖臑居一,不易之率也.”意思是:如图,沿正方体对角面截正方体可得两个堑堵,再沿平面截堑堵可得一个阳马(四棱锥),一个鳖臑(三棱锥.若P为线段CD上一动点,平面过点P,且平面,设正方体棱长为1,,与图中鳖臑截面面积为S,则点P从点D移动到点C的过程中,S关于x的函数图象大致是( )
A. B.
C. D.
二、填空题(本大题共5小题,每小题5分,共25分。请把结果填在答题纸上的相应位置。)
11.已知正方形ABCD的边长为2,则_________.
12.已知某圆锥的轴截面是边长为2的等边三角形,则此圆锥的表面积为___________.
13.平面与平面垂直的判定定理符号语言为:______________________.
14.在移动通信中,总是有很多用户希望能够同享一个发射煤介,进行无线通信,这种通信方式称为多址通信.多址通信的理论基础是若用户之间的信号可以做到正交,这些用户就可以同享一个发射媒介.在n维空间中,正交的定义是两个n维向量满足.己知某通信方式中用户的信号是4维非零向量,有四个用户同享一个发射媒介,已知前三个用户的信号向量为,写出一个满足条件的第四个用户的信号向量____________.
15.一个三棱锥的三个侧面中有一个是边长为2的正三角形,另两个是等腰直角三角形,则该三棱锥的体积可能为___________.
三、解答题(本大题共3小题,共35分。解答应写出文字说明过程或演算步骤,请将答案写在答题纸上的相应位置。)
16.(本题10分)
已知空间直角坐标系中四个点的坐标分别为:,
(I)求;
(II)若,求x的值;
(Ⅲ)若D点在平面ABC上,直接写出x的值.
17.(本题12分)
如图所示,在四棱锥中,平面PAD,,E是PD的中点.
(I)求证:;
(II)求证:平面PAB;
(Ⅲ)若M是线段CE上一动点,则线段AD上是否存在点N,使平面PAB 并说明理由.
18.(本题13分)
如图所示,已知四棱锥中,ABCD是直角梯形,,平面平面ABCD,.
(I)证明:平面ABCD;
(I)求B到平面ADE的距离;
(Ⅲ)求二面角的余弦值.
第Ⅱ卷(共8道题,满分50分)
一、选择题(共4小题,每小题5分,共20分。在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确答案填涂在答题纸上的相应位置。)
19.关于空间中的角,下列说法中正确的个数是( )
①空间中两条直线所成角的取值范围是
②空间中直线与平面所成角的取值范围是
③空间中二面角的平面角的取值范围是
④空间中平面与平面所成角的取值范围是
A.1 B.2 C.3 D.4
20.如图,在正方形ABCD中,点E,F分别为边BC,AD的中点,将沿BF所在直线进行翻折,将沿DE所在直线进行翻折,在翻折的过程中,下列说法正确的是( )
A.点A与点C在某一位置可能重合 B.点A与点C的最大距离为
C.直线AB与直线DE可能垂直 D.直线AF与直线CE可能垂直
21.在正方体中,P为棱上一动点,Q为底面ABCD上一动点,M是线段PQ的中点,若点P,Q都运动时,点M构成的点集是一个空间几何体,则这个几何体是( )
A.棱柱 B.棱台 C.棱锥 D.球的一部分
22.如图,在棱长为2的正方体中,P为线段的中点,Q为线段上的动点,则下列结论正确的是( )
A.存在点Q,使得 B.存在点Q,使得PQ与AD所成的角为
C.三棱锥的体积是定值 D.存在点Q,使得平面
二、填空题(共3小题,每小题5分,共15分。把答案填在答题纸上的相应位置。)
23.如图,在边长为2正方体中,E为BC的中点,点P在正方体表面上移动,且满足,则点和满足条件的所有点P构成的图形的周长是___________.
24.已知正三棱柱的所有侧棱长及底面边长都为2,D是侧棱的中点,则直线AD与平面所成角的正弦值为___________.
25.点O是正四面体的外接球球心,.
若,其中,则动点P扫过的区域的体积为___________.
三、解答题(本小题15分,解答应写出文字说明过程或演算步骤。请将答案写在答题纸上的相应位置。)
26.己知自然数集,非空集合,若集合E满足:对任意,存在,使得,称集合E为集合A的一组m元基底.
(I)分别判断下列集合E是否为集合A的一组二元基底,并说明理由:
①;
②.
(II)若集合E是集合A的一组m元基底,证明:;
(III)若集合E为集合的一组m元基底,求m的最小值.
北京市海淀区重点中学2023-2024学年高二上学期期中练习
数学
参考答案及评分标准
I卷
一、选择题(共10小题,每小题4分,共40分。)
(1)B (2)C (3)B (4)C (5)B (6)C (7)C (8)A (9)C (10)B
二、填空题(共5小题,每小题5分,共25分。)
(11) (12)
(13)若,则
(14)(答案不唯一,即可)
(15)或或(仅看正确答案,答出1个2分,2个3分,答案全对5分)
三、解答题(共3小题,共35分。)
(16)(共10分)
解(I), 1分
3分
(II). 5分
因为,所以 6分
即,解得 7分
(III) 10分
(17)(共12分)
解:(I)因为平面PAD,在四棱锥中, 1分
平面ABCD, 2分
平面平面ABCD, 3分
所以
(II)取F为AP中点,连接EF,BF, 4分
因为E,F是PD,PA的中点.
所以且,
由(I)知,又.
所以四边形BCEF下为平行四边形, 5分
所以,
又平面PAB, 6分
平面PAB,
所以平面PAB 7分
(若用面面平行证明则对应给分;辅助线1分;两个平行各1分,两条相交直线1分)
(III)线段AD存在点N,使得平面PAB,理由如下: 8分
取AD中点N,连接CN,EN,
因为E,N分别为PD,AD的中点,所以,
因为平面PAB,
平面PAB,
所以平面PAB. 10分
由(II)知:平面PAB,
又平面CEN,
所以平面平面PAB,
又M是CE上的动点,平面CEN,
所以平面PAB,所以线段AD存在N,使得面PAB 12分
(18)(共13分)
解:(T)在四棱锥中,
,
因为,由勾股定理逆定理得 1分
又因为平面平面ABCD, 2分
平面平面, 3分
平面EAB, 4分
所以平面ABCD;
(II)由(I)得平面ABCD;
因为BA,平面ABCD,
所以,又,所以EB,BA,BC两两垂直,
以B为原点建立空间直角坐标系如图.
. 5分
设平面ADE的法向量,
,令,得 6分
设B到平面ADE距离为d,,
则 8分
几何法过B作AE的垂线段,直接求出高,
证明是垂线段的过程线面垂直2分,答案2分;
等积法,体积1分,底面积1分,答案2分.
(III)
设平面DEC的法向量,
令,得 10分
, 12分
设二面角为,由图可知为钝角,
故 13分
Ⅱ卷
一、选择题(共4小题,每小题5分,共20分)
(19)C (20)D (21)A (22)D
二、填空题(共3小题,每小题5分,共15分)
(23) (24) (25)
同课章节目录
