江苏省南京市玄武区2023-2024学年八年级上学期期中数学试题(无答案)
文档属性
| 名称 | 江苏省南京市玄武区2023-2024学年八年级上学期期中数学试题(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 972.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-26 21:38:02 | ||
图片预览

文档简介
2023~2024学年第一学期期中学业质量调研
八年级数学
注意事项:
1.本试卷共6页,全卷满分100分,考试时间为100分钟.考生答题全部答在答题卡上,答在本试卷上无效.
2.请认真核对监考教师在答题卡上所粘贴条形码的姓名、考试证号是否与本人相符合,再将自己的姓名、准考证号用0.5毫米黑色墨水签字笔填写在答题卡及本试卷上.
3.答选择题必须用2B铅笔将答题卡上对应的答案标号涂黑.如需改动,请用橡皮擦干净后,再选涂其他答案.答非选择题必须用0.5毫米黑色墨水签字笔写在答题卡上的指定位置,在其他位置答题一律无效.
4.作图必须用2B铅笔作答,并请加黑加粗,描写清楚.
一、选择题(本大题共8小题,每小题2分,共16分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡相应位置上)
1.下列图案中,是轴对称图形的是( )
A. B. C. D.
2.估计的值在( )
A.2到3之间 B.3到4之间 C.4到5之间 D.5到6之间
3.下列长度的三条线段能组成直角三角形的是( )
A.3,4,5 B.4,5,6 C.5,6,7 D.6,7,8
4.如图,在中,,DE垂直平分AC.若,,则的周长是( )
(第4题)
A.6 B.8 C.10 D.12
5.到三角形三个顶点距离相等的点是( )
A.三条高线的交点 B.三边垂直平分线的交点
C.三条角平分线的交点 D.三条中线的交点
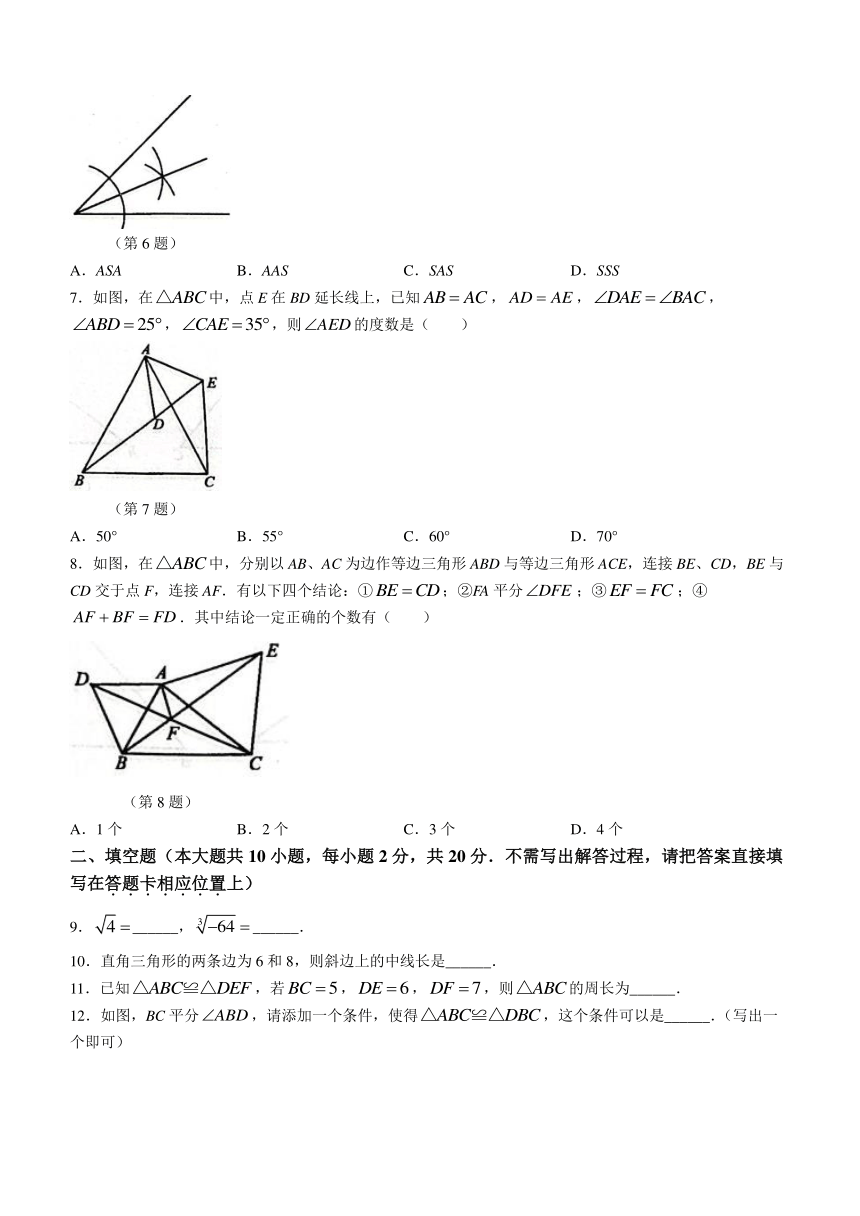
6.如图,用直尺和圆规作一个角的平分线,是运用了“全等三角形的对应角相等”这一性质,由作图所得条件,判定三角形全等运用的方法是( )
(第6题)
A.ASA B.AAS C.SAS D.SSS
7.如图,在中,点E在BD延长线上,已知,,,,,则的度数是( )
(第7题)
A.50° B.55° C.60° D.70°
8.如图,在中,分别以AB、AC为边作等边三角形ABD与等边三角形ACE,连接BE、CD,BE与CD交于点F,连接AF.有以下四个结论:①;②FA平分;③;④.其中结论一定正确的个数有( )
(第8题)
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共10小题,每小题2分,共20分.不需写出解答过程,请把答案直接填写在答题卡相应位置上)
9.______,______.
10.直角三角形的两条边为6和8,则斜边上的中线长是______.
11.已知,若,,,则的周长为______.
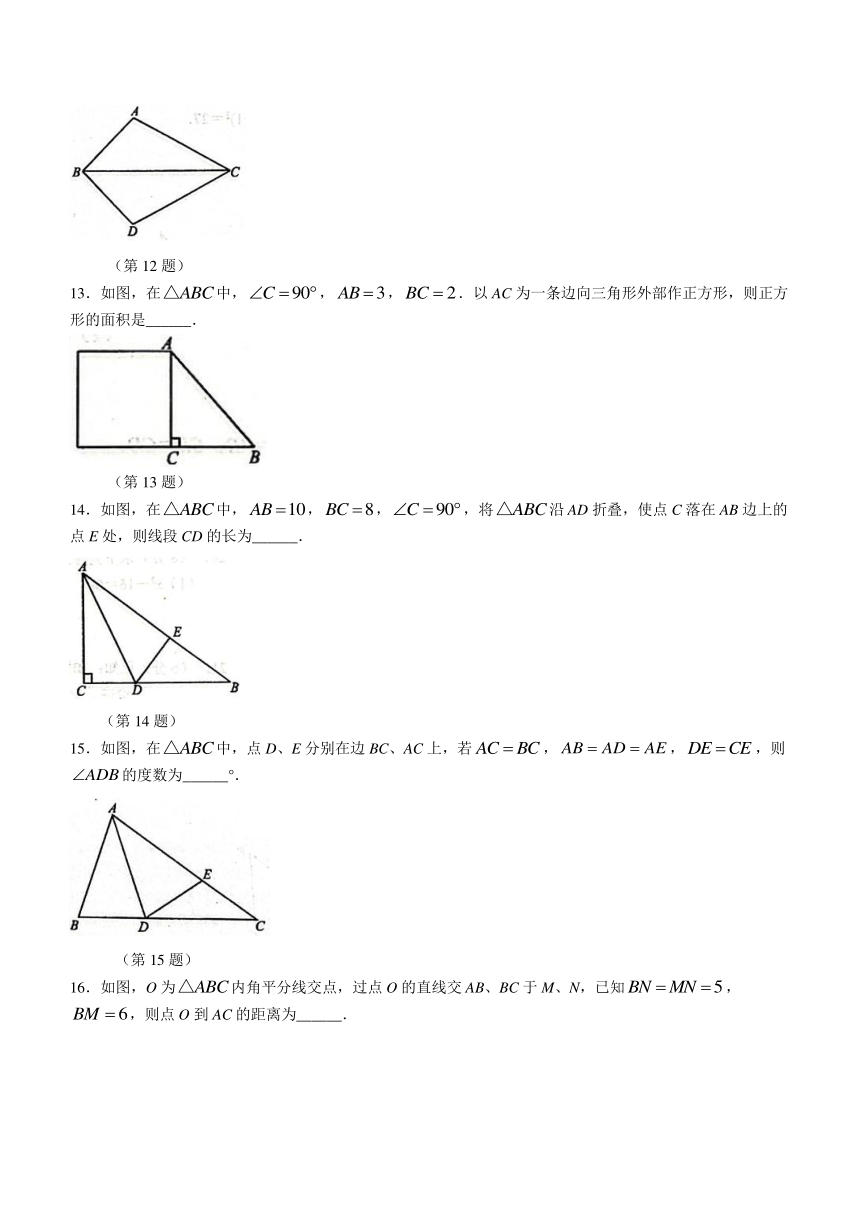
12.如图,BC平分,请添加一个条件,使得,这个条件可以是______.(写出一个即可)
(第12题)
13.如图,在中,,,.以AC为一条边向三角形外部作正方形,则正方形的面积是______.
(第13题)
14.如图,在中,,,,将沿AD折叠,使点C落在AB边上的点E处,则线段CD的长为______.
(第14题)
15.如图,在中,点D、E分别在边BC、AC上,若,,,则的度数为______°.
(第15题)
16.如图,O为内角平分线交点,过点O的直线交AB、BC于M、N,已知,,则点O到AC的距离为______.
(第16题)
17.在中,,,,在边上有一点P,且是等腰三角形,则满足条件的点P的个数为______.
18.如图,中,,,,D、E、F分别是AB、BC、AC边上的动点,则的最小值是______.
(第18题)
三、解答题(本大题共8小题,共64分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)
19.(6分)计算:.
20.(8分)求下列各式中的x:
(1); (2).
21.(6分)已知:如图,,.求证:.
(第21题)
22.(10分)如图,在中,于点D,,,.
(第22题)
(1)求BD的长;
(2)求的面积;
(3)判断的形状.
23.(8分)证明:角平分线上的点到角两边的距离相等.
已知:如图,OC平分,点P是OC任意上一点,,,E、F为垂足.
求证:______.
证明:
(第23题)
24.(8分)如图,四边形CEDF,,,A是边DE上一点,过点C作交DF延长线于点B.
(第24题)
(1)求证:;
(2)设三边分别为a、b、c,利用此图证明勾股定理.
25.(8分)过点P用两种不同的方法,利用直尺和圆规作直线l,交两边于B、C,使得为等腰三角形(保留作图痕迹,不写作法).
(第25题)
26.(10分)通过对下面数学模型的研究学习,解决下列问题:
【模型理解】
(1)如图①,,共顶点A,,,,连BD、CE.由,得.又,,可以推理得到,进而得到______,______.
图①
【问题研究】
(2)小明同学在思考完上述问题后,解决了下面的尺规作图问题.
如图②,已知直线a、b及点P,a与b不平行.作等腰直角,使得点A、B分别在直线a、b上.
图② 图③
小明同学作法简述如下:如图③,过点P作,垂足为点D,以P为直角顶点作等腰直角三角形PDE,过点E作,交b于点B,在a上截取,连AB.即为所要求作的等腰直角三角形.
请证明小明的作法是正确的.
【深入研究】
小明同学经过研究发现:在上题条件下,也能作出等边,使得点A、B分别在直线a、b上.
(3)请你简述作法,并在图④中画出示意图.(不需要尺规作图)
图④
八年级数学
注意事项:
1.本试卷共6页,全卷满分100分,考试时间为100分钟.考生答题全部答在答题卡上,答在本试卷上无效.
2.请认真核对监考教师在答题卡上所粘贴条形码的姓名、考试证号是否与本人相符合,再将自己的姓名、准考证号用0.5毫米黑色墨水签字笔填写在答题卡及本试卷上.
3.答选择题必须用2B铅笔将答题卡上对应的答案标号涂黑.如需改动,请用橡皮擦干净后,再选涂其他答案.答非选择题必须用0.5毫米黑色墨水签字笔写在答题卡上的指定位置,在其他位置答题一律无效.
4.作图必须用2B铅笔作答,并请加黑加粗,描写清楚.
一、选择题(本大题共8小题,每小题2分,共16分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡相应位置上)
1.下列图案中,是轴对称图形的是( )
A. B. C. D.
2.估计的值在( )
A.2到3之间 B.3到4之间 C.4到5之间 D.5到6之间
3.下列长度的三条线段能组成直角三角形的是( )
A.3,4,5 B.4,5,6 C.5,6,7 D.6,7,8
4.如图,在中,,DE垂直平分AC.若,,则的周长是( )
(第4题)
A.6 B.8 C.10 D.12
5.到三角形三个顶点距离相等的点是( )
A.三条高线的交点 B.三边垂直平分线的交点
C.三条角平分线的交点 D.三条中线的交点
6.如图,用直尺和圆规作一个角的平分线,是运用了“全等三角形的对应角相等”这一性质,由作图所得条件,判定三角形全等运用的方法是( )
(第6题)
A.ASA B.AAS C.SAS D.SSS
7.如图,在中,点E在BD延长线上,已知,,,,,则的度数是( )
(第7题)
A.50° B.55° C.60° D.70°
8.如图,在中,分别以AB、AC为边作等边三角形ABD与等边三角形ACE,连接BE、CD,BE与CD交于点F,连接AF.有以下四个结论:①;②FA平分;③;④.其中结论一定正确的个数有( )
(第8题)
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共10小题,每小题2分,共20分.不需写出解答过程,请把答案直接填写在答题卡相应位置上)
9.______,______.
10.直角三角形的两条边为6和8,则斜边上的中线长是______.
11.已知,若,,,则的周长为______.
12.如图,BC平分,请添加一个条件,使得,这个条件可以是______.(写出一个即可)
(第12题)
13.如图,在中,,,.以AC为一条边向三角形外部作正方形,则正方形的面积是______.
(第13题)
14.如图,在中,,,,将沿AD折叠,使点C落在AB边上的点E处,则线段CD的长为______.
(第14题)
15.如图,在中,点D、E分别在边BC、AC上,若,,,则的度数为______°.
(第15题)
16.如图,O为内角平分线交点,过点O的直线交AB、BC于M、N,已知,,则点O到AC的距离为______.
(第16题)
17.在中,,,,在边上有一点P,且是等腰三角形,则满足条件的点P的个数为______.
18.如图,中,,,,D、E、F分别是AB、BC、AC边上的动点,则的最小值是______.
(第18题)
三、解答题(本大题共8小题,共64分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)
19.(6分)计算:.
20.(8分)求下列各式中的x:
(1); (2).
21.(6分)已知:如图,,.求证:.
(第21题)
22.(10分)如图,在中,于点D,,,.
(第22题)
(1)求BD的长;
(2)求的面积;
(3)判断的形状.
23.(8分)证明:角平分线上的点到角两边的距离相等.
已知:如图,OC平分,点P是OC任意上一点,,,E、F为垂足.
求证:______.
证明:
(第23题)
24.(8分)如图,四边形CEDF,,,A是边DE上一点,过点C作交DF延长线于点B.
(第24题)
(1)求证:;
(2)设三边分别为a、b、c,利用此图证明勾股定理.
25.(8分)过点P用两种不同的方法,利用直尺和圆规作直线l,交两边于B、C,使得为等腰三角形(保留作图痕迹,不写作法).
(第25题)
26.(10分)通过对下面数学模型的研究学习,解决下列问题:
【模型理解】
(1)如图①,,共顶点A,,,,连BD、CE.由,得.又,,可以推理得到,进而得到______,______.
图①
【问题研究】
(2)小明同学在思考完上述问题后,解决了下面的尺规作图问题.
如图②,已知直线a、b及点P,a与b不平行.作等腰直角,使得点A、B分别在直线a、b上.
图② 图③
小明同学作法简述如下:如图③,过点P作,垂足为点D,以P为直角顶点作等腰直角三角形PDE,过点E作,交b于点B,在a上截取,连AB.即为所要求作的等腰直角三角形.
请证明小明的作法是正确的.
【深入研究】
小明同学经过研究发现:在上题条件下,也能作出等边,使得点A、B分别在直线a、b上.
(3)请你简述作法,并在图④中画出示意图.(不需要尺规作图)
图④
同课章节目录
