人教版8年级下册数学18.2.2 菱形 学案 (无答案)
文档属性
| 名称 | 人教版8年级下册数学18.2.2 菱形 学案 (无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 170.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-27 08:37:36 | ||
图片预览


文档简介
菱形
班级:_____________姓名:__________________组号:_________
菱形—巩固拓展
一、巩固训练
1.如图菱形ABCD中,∠BAD=120°,AB=2。
求证:(1)△ABC是等边三角形;
(2)求对角线AC和BD的长;
(3)求菱形ABCD的面积。
归纳:菱形的性质:①轴对称图形,对称轴 条;②四条边 ;
③两条对角线 ,并且每条对角线平分 。
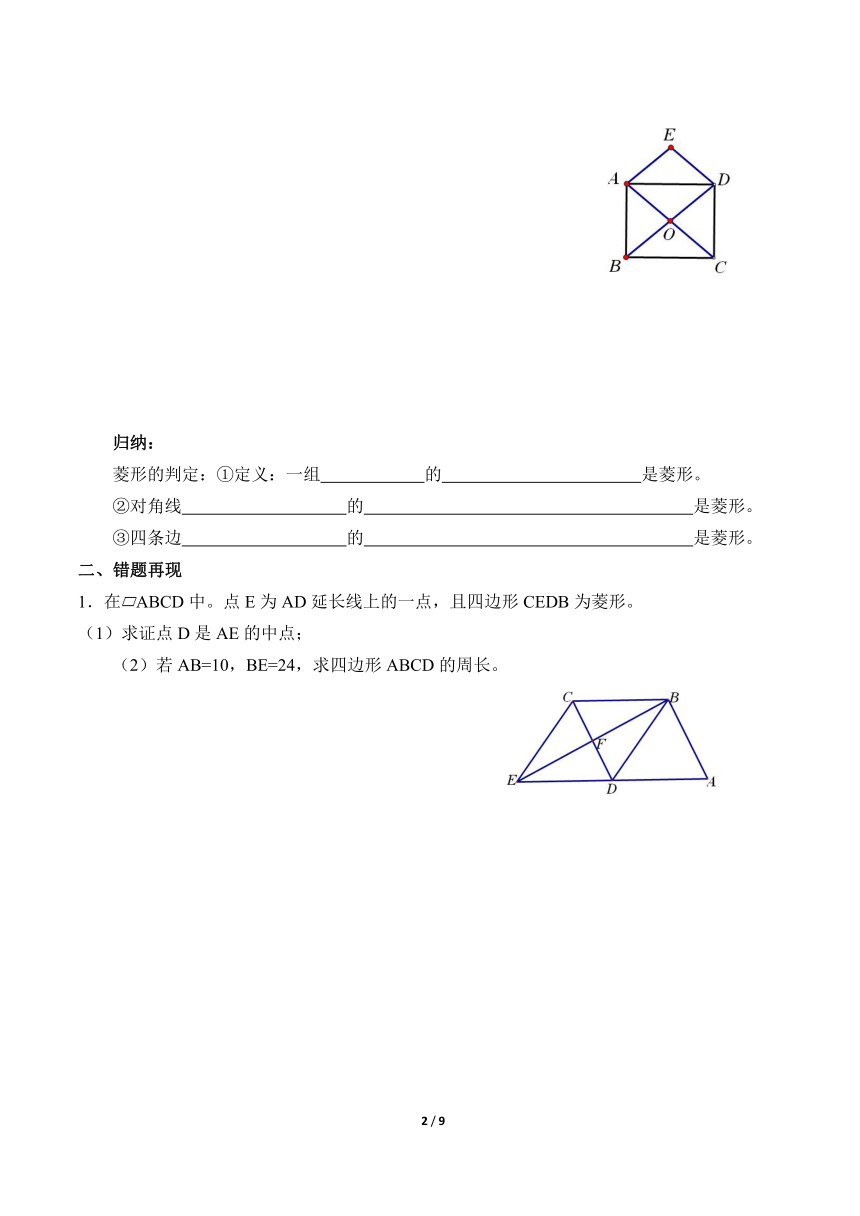
2.矩形ABCD的对角线相交于点O,DE∥CA,AE∥BD,求证四边形AODE是菱形。
归纳:
菱形的判定:①定义:一组 的 是菱形。
②对角线 的 是菱形。
③四条边 的 是菱形。
二、错题再现
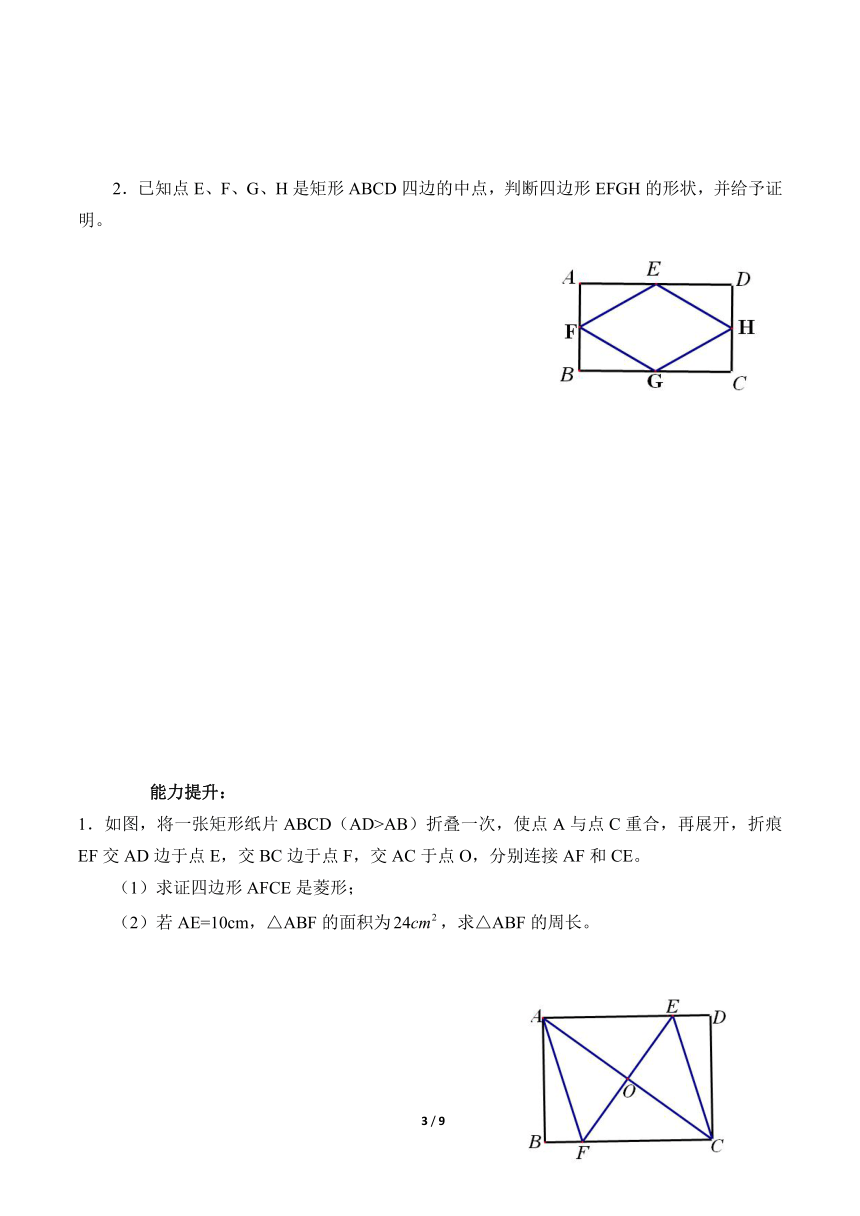
1.在ABCD中。点E为AD延长线上的一点,且四边形CEDB为菱形。
(1)求证点D是AE的中点;
(2)若AB=10,BE=24,求四边形ABCD的周长。
2.已知点E、F、G、H是矩形ABCD四边的中点,判断四边形EFGH的形状,并给予证明。
能力提升:
1.如图,将一张矩形纸片ABCD(AD>AB)折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,交AC于点O,分别连接AF和CE。
(1)求证四边形AFCE是菱形;
(2)若AE=10cm,△ABF的面积为,求△ABF的周长。
四、精练反馈
A组:
1.菱形的两条对角线长分别为6和8,则它的面积为_________,边长为_________。
2.如图,在菱形ABCD中,AB=17,BD=16,点E为对角线BD延长线上的一点,且AE=25,求DE的长。
B组:
3.如图,△ABC与△CDE都是等边三角形,点E、F分别在AC、BC上,且EF∥AB。
(1)求证:四边形EFCD是菱形;
(2)若CD=4,求D、F两点间的距离。
【答案】
【巩固训练】
1.(1)∵四边形ABCD是菱形,∠BAD=120°,
∴AB=BC,∠BAC=∠BAD=60°
∴△ABC是等边三角形;
(2)∵四边形ABCD是菱形,
∴AC⊥BD,
在Rt△ABO中,
∵∠BAC=60°,AB=2cm,
∴∠ABO=30°,
∴OA=AB=1cm
∴OD=
∴AC=2OA=2cm,BD=2OD=2cm。
(3)S=
归纳:①2 ②相等 ③互相垂直平分;每组对角
2.证明:∵DE∥AC,AE∥BD,
∴四边形AODE是平行四边形,
∵ABCD是矩形,∴OA=OD,
∴平行四边形AODE是菱形。
归纳:①邻边相等;平行四边形②互相垂直;平行四边形③都相等;四边形
【错题再现】
1.(1)∵四边形ABCD是平行四边形
∴AD=BC, AB=CD
∵CEDB是菱形
∴BC=DE
∴AD=DE
∴点D就是AE的中点
(2)∵四边形CEDB是菱形
∴BE⊥CD,BF=EF=12
∵四边形ABCD是平行四边形
∴AB=CD=10,CF=FD=5,
在Rt△EFD中,ED==13,
∴ED=AD=13
∴四边形ABCD的周长:13+13+10+10=46
2.解:四边形EFGH菱形
连接对角线AC和BD
∵E,F,G,H是矩形ABCD四边的中点
∴EF和GH分别是△ABD和△CBD的中位线
∴EF=GH= BD
且EF//GH
同理:EH=GF= AC 且EH//GF
又∵AC=BD
∴EF=GH=EH= GF
∴四边形EFGH菱形
【能力提升】
1.(1)证明∵四边形ABCD是矩形,
∴ AD∥ BC,∴∠ EAO=∠ FCO,AE∥ FC
由折叠的性质可得:OA=OC,AC⊥EF,
在△ AOE和△ COF中,
∠ EAO=∠ FCO,OA=OC,∠ AOE=∠ COF
∴ △ AOE≌ △ COF(ASA),
∴ AE=CF,
∴ 四边形AFCE是平行四边形,
∵ AC⊥EF,
∴ 四边形AFCE是菱形;
(2)∵ 四边形AFCE是菱形,
∴ AF=AE=10cm,
∵ 四边形ABCD是矩形,
∴ ∠ B=90°,
∴ S△ ABF=ABBF=24cm ,
∴ ABBF=48(cm ),
∴ AB +BF =(AB+BF) -2ABBF=(AB+BF) -2×48=AF =100(cm ),
∴ AB+BF=14(cm)
∴ △ ABF的周长为:AB+BF+AF=14+10=24(cm)。
【精练反馈】
1.24;5
2.先连接AC交BE于F,
∵ 四边形ABCD是菱形,
∴ AC⊥BD,BF=FD=8
在Rt△ABF中,
AF==15
∴ DF=15
在Rt△ADF中,
FE==20
∴ DE=FE-FD=20-8=12
3.(1)证明:∵△ABC与△CDE都是等边三角形,
∴CD=CE=DE,∠A=∠B=∠ACB=60°,
∵EF∥AB,
∴∠CEF=∠A,∠CFE=∠B
∴∠CEF=∠CFE=∠ACB
∴CE=CF=EF
∴CD=DE=EF=CF
∴四边形EFCD是菱形;
(2)连结DF交CE于O,
∵四边形EFCD是菱形
∴DF⊥CE,OC=OE,OD=OF=DF,DF平分∠CDE
∵∠CDE=60°
∴∠COD=90°,∠CDO=30°
在△COD中,OC=CD=2,
由勾股定理得:OC +OD =CD
∵OC=2,CD=4
∴OD =12
∴OD=2
∴DF=2OD=4
F
O
9 / 9
班级:_____________姓名:__________________组号:_________
菱形—巩固拓展
一、巩固训练
1.如图菱形ABCD中,∠BAD=120°,AB=2。
求证:(1)△ABC是等边三角形;
(2)求对角线AC和BD的长;
(3)求菱形ABCD的面积。
归纳:菱形的性质:①轴对称图形,对称轴 条;②四条边 ;
③两条对角线 ,并且每条对角线平分 。
2.矩形ABCD的对角线相交于点O,DE∥CA,AE∥BD,求证四边形AODE是菱形。
归纳:
菱形的判定:①定义:一组 的 是菱形。
②对角线 的 是菱形。
③四条边 的 是菱形。
二、错题再现
1.在ABCD中。点E为AD延长线上的一点,且四边形CEDB为菱形。
(1)求证点D是AE的中点;
(2)若AB=10,BE=24,求四边形ABCD的周长。
2.已知点E、F、G、H是矩形ABCD四边的中点,判断四边形EFGH的形状,并给予证明。
能力提升:
1.如图,将一张矩形纸片ABCD(AD>AB)折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,交AC于点O,分别连接AF和CE。
(1)求证四边形AFCE是菱形;
(2)若AE=10cm,△ABF的面积为,求△ABF的周长。
四、精练反馈
A组:
1.菱形的两条对角线长分别为6和8,则它的面积为_________,边长为_________。
2.如图,在菱形ABCD中,AB=17,BD=16,点E为对角线BD延长线上的一点,且AE=25,求DE的长。
B组:
3.如图,△ABC与△CDE都是等边三角形,点E、F分别在AC、BC上,且EF∥AB。
(1)求证:四边形EFCD是菱形;
(2)若CD=4,求D、F两点间的距离。
【答案】
【巩固训练】
1.(1)∵四边形ABCD是菱形,∠BAD=120°,
∴AB=BC,∠BAC=∠BAD=60°
∴△ABC是等边三角形;
(2)∵四边形ABCD是菱形,
∴AC⊥BD,
在Rt△ABO中,
∵∠BAC=60°,AB=2cm,
∴∠ABO=30°,
∴OA=AB=1cm
∴OD=
∴AC=2OA=2cm,BD=2OD=2cm。
(3)S=
归纳:①2 ②相等 ③互相垂直平分;每组对角
2.证明:∵DE∥AC,AE∥BD,
∴四边形AODE是平行四边形,
∵ABCD是矩形,∴OA=OD,
∴平行四边形AODE是菱形。
归纳:①邻边相等;平行四边形②互相垂直;平行四边形③都相等;四边形
【错题再现】
1.(1)∵四边形ABCD是平行四边形
∴AD=BC, AB=CD
∵CEDB是菱形
∴BC=DE
∴AD=DE
∴点D就是AE的中点
(2)∵四边形CEDB是菱形
∴BE⊥CD,BF=EF=12
∵四边形ABCD是平行四边形
∴AB=CD=10,CF=FD=5,
在Rt△EFD中,ED==13,
∴ED=AD=13
∴四边形ABCD的周长:13+13+10+10=46
2.解:四边形EFGH菱形
连接对角线AC和BD
∵E,F,G,H是矩形ABCD四边的中点
∴EF和GH分别是△ABD和△CBD的中位线
∴EF=GH= BD
且EF//GH
同理:EH=GF= AC 且EH//GF
又∵AC=BD
∴EF=GH=EH= GF
∴四边形EFGH菱形
【能力提升】
1.(1)证明∵四边形ABCD是矩形,
∴ AD∥ BC,∴∠ EAO=∠ FCO,AE∥ FC
由折叠的性质可得:OA=OC,AC⊥EF,
在△ AOE和△ COF中,
∠ EAO=∠ FCO,OA=OC,∠ AOE=∠ COF
∴ △ AOE≌ △ COF(ASA),
∴ AE=CF,
∴ 四边形AFCE是平行四边形,
∵ AC⊥EF,
∴ 四边形AFCE是菱形;
(2)∵ 四边形AFCE是菱形,
∴ AF=AE=10cm,
∵ 四边形ABCD是矩形,
∴ ∠ B=90°,
∴ S△ ABF=ABBF=24cm ,
∴ ABBF=48(cm ),
∴ AB +BF =(AB+BF) -2ABBF=(AB+BF) -2×48=AF =100(cm ),
∴ AB+BF=14(cm)
∴ △ ABF的周长为:AB+BF+AF=14+10=24(cm)。
【精练反馈】
1.24;5
2.先连接AC交BE于F,
∵ 四边形ABCD是菱形,
∴ AC⊥BD,BF=FD=8
在Rt△ABF中,
AF==15
∴ DF=15
在Rt△ADF中,
FE==20
∴ DE=FE-FD=20-8=12
3.(1)证明:∵△ABC与△CDE都是等边三角形,
∴CD=CE=DE,∠A=∠B=∠ACB=60°,
∵EF∥AB,
∴∠CEF=∠A,∠CFE=∠B
∴∠CEF=∠CFE=∠ACB
∴CE=CF=EF
∴CD=DE=EF=CF
∴四边形EFCD是菱形;
(2)连结DF交CE于O,
∵四边形EFCD是菱形
∴DF⊥CE,OC=OE,OD=OF=DF,DF平分∠CDE
∵∠CDE=60°
∴∠COD=90°,∠CDO=30°
在△COD中,OC=CD=2,
由勾股定理得:OC +OD =CD
∵OC=2,CD=4
∴OD =12
∴OD=2
∴DF=2OD=4
F
O
9 / 9
