初中数学人教版八年级上册13.3.2 等边三角形(1)》课件 16张PPT
文档属性
| 名称 | 初中数学人教版八年级上册13.3.2 等边三角形(1)》课件 16张PPT |  | |
| 格式 | pptx | ||
| 文件大小 | 13.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-27 11:06:19 | ||
图片预览






文档简介
(共16张PPT)
13.3.2 等边三角形
0
第一课时
我们在前面的两节课研究并证明了等腰三角形的性质和判定定理,我们知道,在等腰三角形中有一种特殊的等腰三角形-----等边三角形。下面,我们先来回顾一下等腰三角形的相关知识。
谈话导入
知识回顾
问题探究
课堂小结
随堂检测
0
(1)等腰三角形的定义:有两边_______的三角形叫做等腰三角形.
(2)等腰三角形的性质:
①等边对_________;
②等腰三角形的______________、______________、 ______________互相重合.
(3)等腰三角形的判定:等角对_________.
相等
等角
顶角平分线
底边上的中线
底边上的高
等边
知识回顾
问题探究
课堂小结
随堂检测
活动1
0
探究一:等边三角形的性质
在等腰三角形中,如果底边也等于腰长,会得到哪些结论呢?类比等腰三角形的定义,给等边三角形下一个定义。
定义:三条边都相等的三角形,叫等边三角形。
这是什么类型的问题?怎么证明呢?有哪些步骤呢?
画草图,写出已知求证,最后证明.
知识回顾
问题探究
课堂小结
随堂检测
活动1
0
探究一:等边三角形的性质
三条边相等
等角
三角形的内角和
练习:等边三角形 轴对称图形(填是或否).如果是,
它有 条对称轴,分别是
.
是
3
三个角的平分线(或三条边的中线或三条边的高线)所在的直线
知识回顾
问题探究
课堂小结
随堂检测
活动1
0
探究二:等边三角形的判定
探究判定1
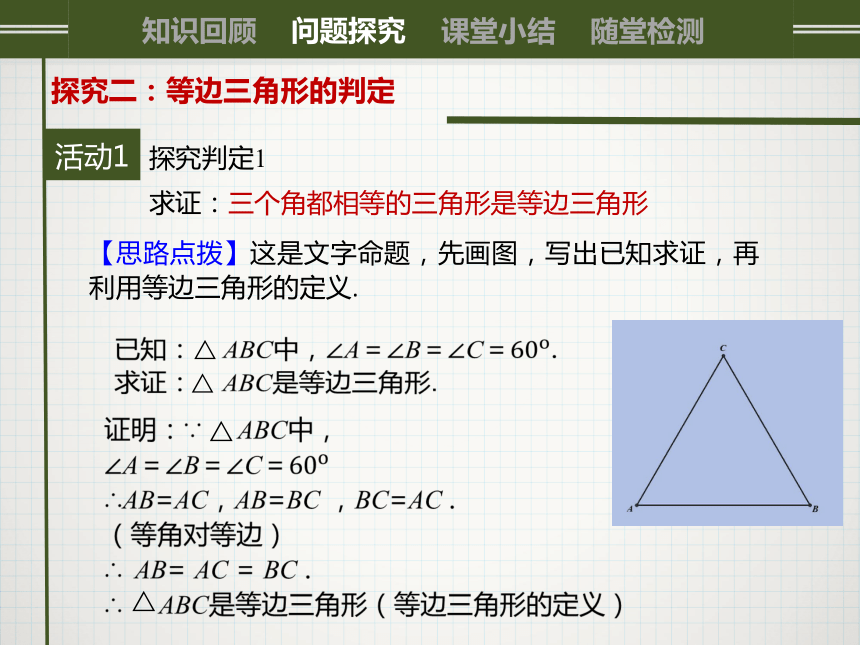
求证:三个角都相等的三角形是等边三角形
【思路点拨】这是文字命题,先画图,写出已知求证,再利用等边三角形的定义.
知识回顾
问题探究
课堂小结
随堂检测
活动2
0
探究二:等边三角形的判定
探究判定2
【思路点拨】这是文字命题,先画图,写出已知求证,再利用等边三角形的定义.
相等
知识回顾
问题探究
课堂小结
随堂检测
0
探究三:等边三角形的性质和判定运用
【思路点拨】先利用等边三角形的性质得出三个内角相等,再由平行线的性质得出∠ADE=∠B ,∠AED=∠C,最后再由等量代换得出小三角形的三个内角相等,再由等边三角形的判定1得证.
活动1
例1 如图, ABC是等边三角形,DE∥BC,分别交AB,AC于点D,E.
求证: ADE是等边三角形.
知识回顾
问题探究
课堂小结
随堂检测
0
探究三:等边三角形的性质和判定运用
活动1
例1 如图, ABC是等边三角形,DE∥BC,分别交AB,AC于点D,E.
求证: ADE是等边三角形.
证明:
∵ ABC是等边三角形,
∴∠A=∠B =∠C
(等边三角形的三个内角相等 )
∵DE∥BC,
∴∠ADE=∠B ,∠AED=∠C .
(两直线平行,同位角相等 )
∴∠A=∠ADE =∠AED .
∴ ADE是等边三角形
(三个角都相等的三角形是等边三角形)
知识回顾
问题探究
课堂小结
随堂检测
0
探究三:等边三角形的性质和判定运用
活动2
思维拓展
对于例1你还有其他方法证明吗?
知识回顾
问题探究
课堂小结
随堂检测
0
探究三:等边三角形的性质和判定运用
活动2
练习:如图,在等边三角形ABC的三边上,分别取点D,E,F,使AD=BE=CF.
求证: DEF是等边三角形.
【思路点拨】 先由 ABC是等边三角形,得出AB=BC=AC,∠A=∠B=∠C,再由已知AD=BE=CF和等式性质即可得出BD=EC=AF,最后由三角形全等得证.
知识回顾
问题探究
课堂小结
随堂检测
0
探究三:等边三角形的性质和判定运用
活动2
练习:如图,在等边三角形ABC的三边上,分别取点D,E,F,使AD=BE=CF.
求证: DEF是等边三角形.
证明:∵ ABC是等边三角形
∴AB=BC=AC,∠A=∠B=∠C
又∵AD=BE=CF
∴BD=EC=AF
∴ DBE≌ ECF≌ FAD(SAS)
∴DE=EF=DF
∴ DEF是等边三角形
知识梳理
知识回顾
问题探究
课堂小结
随堂检测
0
重难点归纳
问题探究
课堂小结
0
等腰三角形与等边三角形的区别和联系
等腰三角形 等边三角形
区别 性质 边 两边相等 三边相等
角 两个底角相等
三线合一 底边上的中线、高、和顶角的平分线互相重合 每一边上的中线、高和这一边所对的角的平分线互相重合
对称性 是轴对称图形,有1条对称轴 是轴对称图形,有3条对称轴
判定 边 有两条边相等的三角形是等腰三角形(定义法) 三边都相等的三角形是等边三角形(定义)
角 有两个角相等的三角形是等腰三角形(判定)
联系 等腰三角形包括等边三角形,等边三角形是一种特殊的等腰三角形 练习: 我的作业的相关内容
作业:1、教材练习题
2 、自行补充
谢谢大家的聆听
13.3.2 等边三角形
0
第一课时
我们在前面的两节课研究并证明了等腰三角形的性质和判定定理,我们知道,在等腰三角形中有一种特殊的等腰三角形-----等边三角形。下面,我们先来回顾一下等腰三角形的相关知识。
谈话导入
知识回顾
问题探究
课堂小结
随堂检测
0
(1)等腰三角形的定义:有两边_______的三角形叫做等腰三角形.
(2)等腰三角形的性质:
①等边对_________;
②等腰三角形的______________、______________、 ______________互相重合.
(3)等腰三角形的判定:等角对_________.
相等
等角
顶角平分线
底边上的中线
底边上的高
等边
知识回顾
问题探究
课堂小结
随堂检测
活动1
0
探究一:等边三角形的性质
在等腰三角形中,如果底边也等于腰长,会得到哪些结论呢?类比等腰三角形的定义,给等边三角形下一个定义。
定义:三条边都相等的三角形,叫等边三角形。
这是什么类型的问题?怎么证明呢?有哪些步骤呢?
画草图,写出已知求证,最后证明.
知识回顾
问题探究
课堂小结
随堂检测
活动1
0
探究一:等边三角形的性质
三条边相等
等角
三角形的内角和
练习:等边三角形 轴对称图形(填是或否).如果是,
它有 条对称轴,分别是
.
是
3
三个角的平分线(或三条边的中线或三条边的高线)所在的直线
知识回顾
问题探究
课堂小结
随堂检测
活动1
0
探究二:等边三角形的判定
探究判定1
求证:三个角都相等的三角形是等边三角形
【思路点拨】这是文字命题,先画图,写出已知求证,再利用等边三角形的定义.
知识回顾
问题探究
课堂小结
随堂检测
活动2
0
探究二:等边三角形的判定
探究判定2
【思路点拨】这是文字命题,先画图,写出已知求证,再利用等边三角形的定义.
相等
知识回顾
问题探究
课堂小结
随堂检测
0
探究三:等边三角形的性质和判定运用
【思路点拨】先利用等边三角形的性质得出三个内角相等,再由平行线的性质得出∠ADE=∠B ,∠AED=∠C,最后再由等量代换得出小三角形的三个内角相等,再由等边三角形的判定1得证.
活动1
例1 如图, ABC是等边三角形,DE∥BC,分别交AB,AC于点D,E.
求证: ADE是等边三角形.
知识回顾
问题探究
课堂小结
随堂检测
0
探究三:等边三角形的性质和判定运用
活动1
例1 如图, ABC是等边三角形,DE∥BC,分别交AB,AC于点D,E.
求证: ADE是等边三角形.
证明:
∵ ABC是等边三角形,
∴∠A=∠B =∠C
(等边三角形的三个内角相等 )
∵DE∥BC,
∴∠ADE=∠B ,∠AED=∠C .
(两直线平行,同位角相等 )
∴∠A=∠ADE =∠AED .
∴ ADE是等边三角形
(三个角都相等的三角形是等边三角形)
知识回顾
问题探究
课堂小结
随堂检测
0
探究三:等边三角形的性质和判定运用
活动2
思维拓展
对于例1你还有其他方法证明吗?
知识回顾
问题探究
课堂小结
随堂检测
0
探究三:等边三角形的性质和判定运用
活动2
练习:如图,在等边三角形ABC的三边上,分别取点D,E,F,使AD=BE=CF.
求证: DEF是等边三角形.
【思路点拨】 先由 ABC是等边三角形,得出AB=BC=AC,∠A=∠B=∠C,再由已知AD=BE=CF和等式性质即可得出BD=EC=AF,最后由三角形全等得证.
知识回顾
问题探究
课堂小结
随堂检测
0
探究三:等边三角形的性质和判定运用
活动2
练习:如图,在等边三角形ABC的三边上,分别取点D,E,F,使AD=BE=CF.
求证: DEF是等边三角形.
证明:∵ ABC是等边三角形
∴AB=BC=AC,∠A=∠B=∠C
又∵AD=BE=CF
∴BD=EC=AF
∴ DBE≌ ECF≌ FAD(SAS)
∴DE=EF=DF
∴ DEF是等边三角形
知识梳理
知识回顾
问题探究
课堂小结
随堂检测
0
重难点归纳
问题探究
课堂小结
0
等腰三角形与等边三角形的区别和联系
等腰三角形 等边三角形
区别 性质 边 两边相等 三边相等
角 两个底角相等
三线合一 底边上的中线、高、和顶角的平分线互相重合 每一边上的中线、高和这一边所对的角的平分线互相重合
对称性 是轴对称图形,有1条对称轴 是轴对称图形,有3条对称轴
判定 边 有两条边相等的三角形是等腰三角形(定义法) 三边都相等的三角形是等边三角形(定义)
角 有两个角相等的三角形是等腰三角形(判定)
联系 等腰三角形包括等边三角形,等边三角形是一种特殊的等腰三角形 练习: 我的作业的相关内容
作业:1、教材练习题
2 、自行补充
谢谢大家的聆听
