人教版8年级下册数学 第十八章 平行四边形 学案
文档属性
| 名称 | 人教版8年级下册数学 第十八章 平行四边形 学案 |  | |
| 格式 | doc | ||
| 文件大小 | 163.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-27 12:18:20 | ||
图片预览

文档简介
四边形全章复习
【学情分析】:
四边形既是几何中的基本图形,也是“图形与几何”领域的主要研究对象之一。这章平行四边形与各种特殊的平行四边形概念之间重叠交错,容易混淆。对于功底扎实的学生,有时也分清他不们之间的从属关系。因此,本节课通过复习和习题,不仅使学生疏通了知识,也提高了思维能力,更进一步体现了思维的深刻性和批判性。
【教学目标】:
1.通过复习使学生进一步理解平行四边形、矩形、菱形、正方形、梯形的概念,了解它们之间的关系。
2.进一步运用平行四边形、矩形、菱形、正方形、等腰梯形的性质和判定进行简单的证明和计算;
3.进一步提高学生的逻辑推理能力和逻辑表达能力,使学生掌握几何证明中的分析、综合、转化、分类等数学思想;进一步渗透数学的形式美和内涵美、抽象美和逻辑美,提高学生数学美的鉴赏能力。
【教学重点】:平行四边形的概念、性质和判定及与其它图形之间的联系。
【教学难点】:思维能力、推理能力的的提高。
【教学突破点】:用框架图使本章知识条理化、系统化.
【教法、学法设计】: 1.教法:引导复习法,指导归纳总结法,综合练习法。2.学法:主动归纳总结复习法,反思学习法,主动练习法。
【课前准备】:课件
【教学过程设计】:
教学环节 教学活动 设计意图
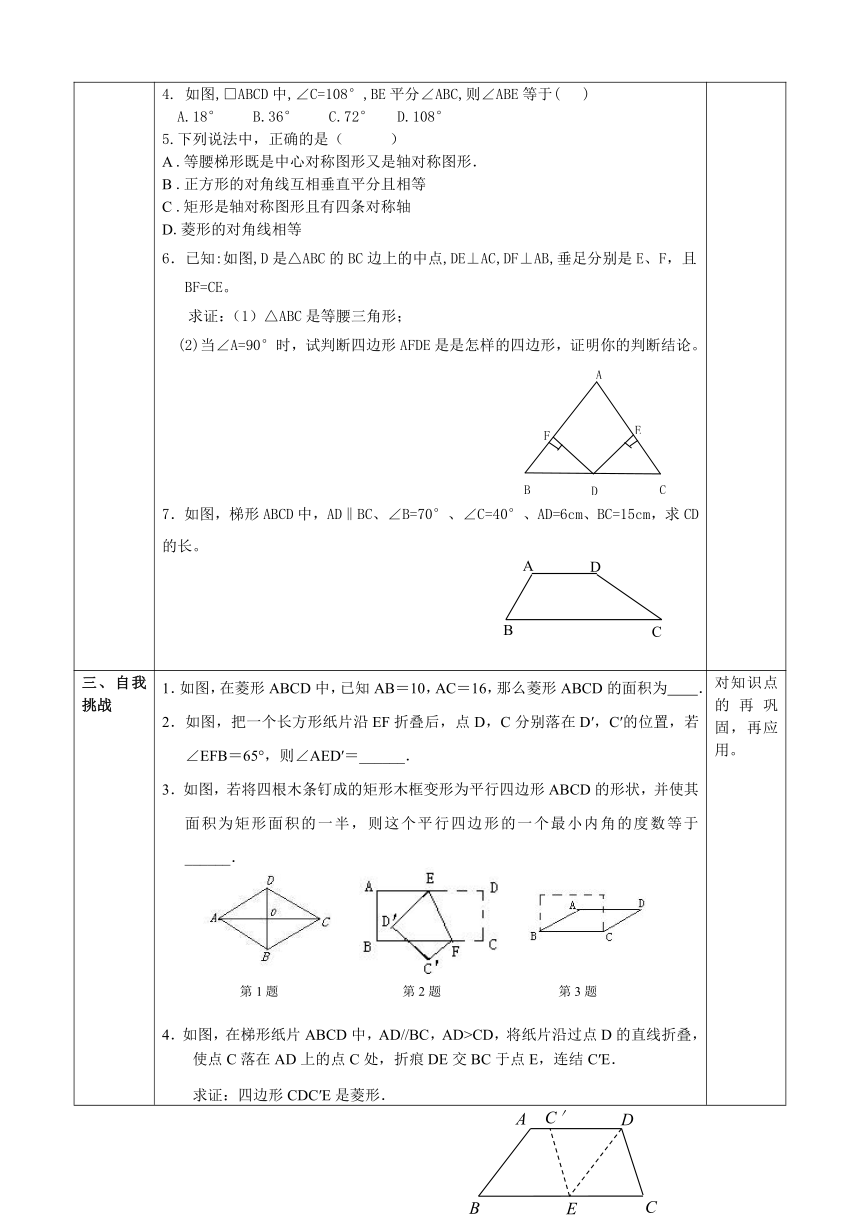
一、知识结构 梳理知识系统
二、基础过关 1. 有以下四个命题:(1)两条对角线互相平分的四边形是平行四边形.(2)两条对角线相等的四边形是菱形.(3)两条对角线互相垂直的四边形是正方形.(4)两条对角线相等且互相垂直的四边形是正方形,其中正确的个数为( )A.4 B.3 C.2 D.12.下面条件中,能判定四边形是平行四边形的条件是( ) A.一组对角相等 B.对角线互相平分 C.一组对边相等 D.对角线互相垂直3.在一个平面上有不在同一直线上的三点,则以这三点为顶点的平行四边形有( )A.1个 B.2个 C.3个 D.4个4. 如图,□ABCD中,∠C=108°,BE平分∠ABC,则∠ABE等于( )A.18° B.36° C.72° D.108°5.下列说法中,正确的是( ) B
A .等腰梯形既是中心对称图形又是轴对称图形.
B .正方形的对角线互相垂直平分且相等
C .矩形是轴对称图形且有四条对称轴
D.菱形的对角线相等6.已知:如图,D是△ABC的BC边上的中点,DE⊥AC,DF⊥AB,垂足分别是E、F,且BF=CE。求证:(1)△ABC是等腰三角形; (2)当∠A=90°时,试判断四边形AFDE是是怎样的四边形,证明你的判断结论。7.如图,梯形ABCD中,AD‖BC、∠B=70°、∠C=40°、AD=6cm、BC=15cm,求CD的长。 对知识点的再巩固,再应用。
三、自我挑战 1.如图,在菱形ABCD中,已知AB=10,AC=16,那么菱形ABCD的面积为 .2.如图,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置,若∠EFB=65°,则∠AED′=______.3.如图,若将四根木条钉成的矩形木框变形为平行四边形ABCD的形状,并使其面积为矩形面积的一半,则这个平行四边形的一个最小内角的度数等于______.4.如图,在梯形纸片ABCD中,AD//BC,AD>CD,将纸片沿过点D的直线折叠,使点C落在AD上的点C处,折痕DE交BC于点E,连结C′E.求证:四边形CDC′E是菱形.5.如图,正方形ABCD中,E为CD上一点,F是BC延长线上一点,CE=CF。(1) 求证△BCE≌△DCF;(2) 若∠BEC=60°,求∠EFD的度数。 对知识点的再巩固,再应用。
四、小结 让学生作解题后的小结,回顾解题过程,总结解题经验和体会,谈谈在本堂课中的体验、收获,不单是知识上的收获,更重要的是能力上的提高,数学思想、方法的领悟,过程的体验与感受。
五、作业 见后附课后练习 巩固提高
课后练习:
1.如图,在平行四边形ABCD中,EF∥BC,GH∥AB,EF、GH的交点P在BD上,图中面积相等的四边形共有( )
A.2对; B.3对; C.4对; D.5对.
2.已知△ABC中,AB=8,AC=6,AD是中线,则AD的取值范围是( )
A. B. C. D.
3.等腰梯形各边中点的连线组成的四边形为( )
A. 矩形 B. 菱形 C. 正方形 D. 等腰梯形
4.已知菱形的周长为,面积为16,则这个菱形较短的对角线长为( )
A.4 B.8 C. D.10
5.如图,面积为16的平行边形ABCD的两条对角线AC、BD交于点O,EF经过点O,且与AB、CD分别交于点E、点F,则图中阴影部分的面积为___________
6.如图,已知图中每个小正方形方格的边长为1,则点C到AB所在直线的距离等于_______
7.如图,点P是边长为2的正方形ABCD的对角线AC上一动点,M、N分别为AB、BC的中点,则MP+NP的最小值为____________
8.如图,在梯形纸片ABCD中,AD∥BC,AD > CD,将纸片沿过点D的直线折叠,使点C落在AD上的点C′处,折痕DE交BC于点E,连结C’E
(1)求证:四边形CDC’E是菱形;
(2)若BC = CD + AD,试判断四边形ABED的形状,并加以证明.
( http: / / www.1230.org )
答案:1.D 2.B 3.B 4.A 5.4 6. 7.2
8.(1)证明:根据题意,可知:CD = C’D,∠C’DE =∠CDE,CE = C’E,
∵ AD∥BC, ∴ ∠C’DE =∠CED. ∴ ∠CDE =∠CED. ∴ CD = CE.
∴ CD = C’D = C’E = CE. ∴ 四边形CDC’E为菱形.
(2)答:当BC = CD + AD时,四边形ABED是平行四边形.
证明:由(1)知CE = CD. ∵ BC = CD + AD, ∴ AD = BE.
又∵ AD∥BE, ∴ 四边形ABED为平行四边形.
26.(1)①S阴影=
②连结PP′,证△PBP′为等腰直角三角形,从而PC=6;
(2)将△PAB绕点B顺时针旋转90°到△P′CB的位置,由勾股逆定理证出∠P′CP=90°,再证∠BPC+∠APB=180°,即点P在对角线AC上.
A
D
B
C
第1题 第2题 第3题
A
D
E
B
C
C′
【学情分析】:
四边形既是几何中的基本图形,也是“图形与几何”领域的主要研究对象之一。这章平行四边形与各种特殊的平行四边形概念之间重叠交错,容易混淆。对于功底扎实的学生,有时也分清他不们之间的从属关系。因此,本节课通过复习和习题,不仅使学生疏通了知识,也提高了思维能力,更进一步体现了思维的深刻性和批判性。
【教学目标】:
1.通过复习使学生进一步理解平行四边形、矩形、菱形、正方形、梯形的概念,了解它们之间的关系。
2.进一步运用平行四边形、矩形、菱形、正方形、等腰梯形的性质和判定进行简单的证明和计算;
3.进一步提高学生的逻辑推理能力和逻辑表达能力,使学生掌握几何证明中的分析、综合、转化、分类等数学思想;进一步渗透数学的形式美和内涵美、抽象美和逻辑美,提高学生数学美的鉴赏能力。
【教学重点】:平行四边形的概念、性质和判定及与其它图形之间的联系。
【教学难点】:思维能力、推理能力的的提高。
【教学突破点】:用框架图使本章知识条理化、系统化.
【教法、学法设计】: 1.教法:引导复习法,指导归纳总结法,综合练习法。2.学法:主动归纳总结复习法,反思学习法,主动练习法。
【课前准备】:课件
【教学过程设计】:
教学环节 教学活动 设计意图
一、知识结构 梳理知识系统
二、基础过关 1. 有以下四个命题:(1)两条对角线互相平分的四边形是平行四边形.(2)两条对角线相等的四边形是菱形.(3)两条对角线互相垂直的四边形是正方形.(4)两条对角线相等且互相垂直的四边形是正方形,其中正确的个数为( )A.4 B.3 C.2 D.12.下面条件中,能判定四边形是平行四边形的条件是( ) A.一组对角相等 B.对角线互相平分 C.一组对边相等 D.对角线互相垂直3.在一个平面上有不在同一直线上的三点,则以这三点为顶点的平行四边形有( )A.1个 B.2个 C.3个 D.4个4. 如图,□ABCD中,∠C=108°,BE平分∠ABC,则∠ABE等于( )A.18° B.36° C.72° D.108°5.下列说法中,正确的是( ) B
A .等腰梯形既是中心对称图形又是轴对称图形.
B .正方形的对角线互相垂直平分且相等
C .矩形是轴对称图形且有四条对称轴
D.菱形的对角线相等6.已知:如图,D是△ABC的BC边上的中点,DE⊥AC,DF⊥AB,垂足分别是E、F,且BF=CE。求证:(1)△ABC是等腰三角形; (2)当∠A=90°时,试判断四边形AFDE是是怎样的四边形,证明你的判断结论。7.如图,梯形ABCD中,AD‖BC、∠B=70°、∠C=40°、AD=6cm、BC=15cm,求CD的长。 对知识点的再巩固,再应用。
三、自我挑战 1.如图,在菱形ABCD中,已知AB=10,AC=16,那么菱形ABCD的面积为 .2.如图,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置,若∠EFB=65°,则∠AED′=______.3.如图,若将四根木条钉成的矩形木框变形为平行四边形ABCD的形状,并使其面积为矩形面积的一半,则这个平行四边形的一个最小内角的度数等于______.4.如图,在梯形纸片ABCD中,AD//BC,AD>CD,将纸片沿过点D的直线折叠,使点C落在AD上的点C处,折痕DE交BC于点E,连结C′E.求证:四边形CDC′E是菱形.5.如图,正方形ABCD中,E为CD上一点,F是BC延长线上一点,CE=CF。(1) 求证△BCE≌△DCF;(2) 若∠BEC=60°,求∠EFD的度数。 对知识点的再巩固,再应用。
四、小结 让学生作解题后的小结,回顾解题过程,总结解题经验和体会,谈谈在本堂课中的体验、收获,不单是知识上的收获,更重要的是能力上的提高,数学思想、方法的领悟,过程的体验与感受。
五、作业 见后附课后练习 巩固提高
课后练习:
1.如图,在平行四边形ABCD中,EF∥BC,GH∥AB,EF、GH的交点P在BD上,图中面积相等的四边形共有( )
A.2对; B.3对; C.4对; D.5对.
2.已知△ABC中,AB=8,AC=6,AD是中线,则AD的取值范围是( )
A. B. C. D.
3.等腰梯形各边中点的连线组成的四边形为( )
A. 矩形 B. 菱形 C. 正方形 D. 等腰梯形
4.已知菱形的周长为,面积为16,则这个菱形较短的对角线长为( )
A.4 B.8 C. D.10
5.如图,面积为16的平行边形ABCD的两条对角线AC、BD交于点O,EF经过点O,且与AB、CD分别交于点E、点F,则图中阴影部分的面积为___________
6.如图,已知图中每个小正方形方格的边长为1,则点C到AB所在直线的距离等于_______
7.如图,点P是边长为2的正方形ABCD的对角线AC上一动点,M、N分别为AB、BC的中点,则MP+NP的最小值为____________
8.如图,在梯形纸片ABCD中,AD∥BC,AD > CD,将纸片沿过点D的直线折叠,使点C落在AD上的点C′处,折痕DE交BC于点E,连结C’E
(1)求证:四边形CDC’E是菱形;
(2)若BC = CD + AD,试判断四边形ABED的形状,并加以证明.
( http: / / www.1230.org )
答案:1.D 2.B 3.B 4.A 5.4 6. 7.2
8.(1)证明:根据题意,可知:CD = C’D,∠C’DE =∠CDE,CE = C’E,
∵ AD∥BC, ∴ ∠C’DE =∠CED. ∴ ∠CDE =∠CED. ∴ CD = CE.
∴ CD = C’D = C’E = CE. ∴ 四边形CDC’E为菱形.
(2)答:当BC = CD + AD时,四边形ABED是平行四边形.
证明:由(1)知CE = CD. ∵ BC = CD + AD, ∴ AD = BE.
又∵ AD∥BE, ∴ 四边形ABED为平行四边形.
26.(1)①S阴影=
②连结PP′,证△PBP′为等腰直角三角形,从而PC=6;
(2)将△PAB绕点B顺时针旋转90°到△P′CB的位置,由勾股逆定理证出∠P′CP=90°,再证∠BPC+∠APB=180°,即点P在对角线AC上.
A
D
B
C
第1题 第2题 第3题
A
D
E
B
C
C′
