人教版8年级下册数学 第十八章 平行四边形 学案(无答案)
文档属性
| 名称 | 人教版8年级下册数学 第十八章 平行四边形 学案(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 46.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-27 14:08:14 | ||
图片预览

文档简介
《平行四边形复习课》导学案
班级 : 组别: 组名: 姓名:
【学习目标】
1、掌握平行四边形、矩形、菱形、正方形的概念、性质和判定,并能灵活运用其进行有关论证和计算
2、理解平行四边形、矩形、菱形、正方形的区别与联系
【重点难点】
重点:平行四边形知识体系的结构化整理
难点:平行四边形知识的选择性应用
【学法指导】小组合作、分组展示
【知识链接】平行四边形、矩形、菱形、正方形的概念、性质和判定
【学习过程】
一、【自学】请阅读课本P66的内容,尝试完成以下问题:
知识点一:平行四边形的知识结构图
问题1:完成平行四边形知识结构定义图
问题2:完成平行四边形关系图
知识点二:平行四边形、矩形、菱形、正方形的性质
四边形 边 角 对 角 线 对称性
平行四边形
矩形
菱形
正方形
知识点三:平行四边形、矩形、菱形、正方形的判定方法
四边形 判 定 方 法
平行四边形
矩 形
菱 形
正 方 形
二、【知识应用】
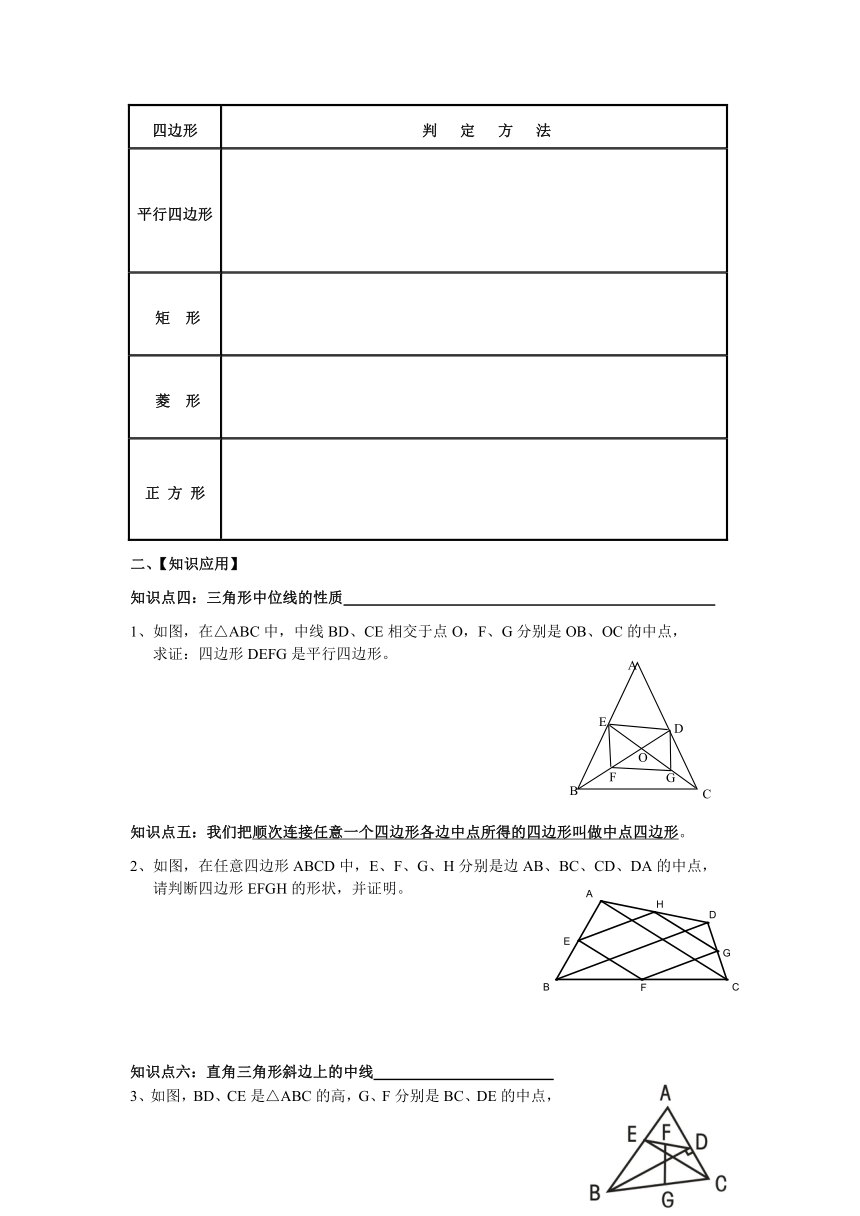
知识点四:三角形中位线的性质
(
A
B
C
D
E
F
G
O
)1、如图,在△ABC中,中线BD、CE相交于点O,F、G分别是OB、OC的中点,
求证:四边形DEFG是平行四边形。
知识点五:我们把顺次连接任意一个四边形各边中点所得的四边形叫做中点四边形。
2、如图,在任意四边形ABCD中,E、F、G、H分别是边AB、BC、CD、DA的中点,
请判断四边形EFGH的形状,并证明。
知识点六:直角三角形斜边上的中线
3、如图,BD、CE是△ABC的高,G、F分别是BC、DE的中点,
求证:FG⊥DE。(连接EG、DG)
三、【基础达标】
1、Rt△OAB的两条直角边在坐标轴上,已知点A(2,0),点B(0,3),则以点O,A,B为其中三个顶点的平行四边形的第四个顶点C的坐标为__________ _。
(
A
B
C
E
F
G
D
)2、如图,把两个大小完全相同的矩形拼成“L”型图案,
则∠FAC= , ∠FCA= 。
3、矩形的一条角平分线分矩形的一边为1和3两部分,则这个矩形的面积为 。
4、菱形的面积是24cm2,一条对角线长为6cm,则菱形的高为 。
知识点七:菱形面积的2种求法:(1) (2) 。
(
A
C
D
B
P
E
F
)5、如图,P在正方形ABCD的对角线BD上一个动点,且PE⊥BC于E,PF⊥CD于F,AB=5cm,则四边形PECF的周长是 。
四、【课堂小结】
知识小结:
方法小结:
五、【当堂检测】
1、如图,在平行四边形ABCD中,两对角线AC、BD相交于点O,且△AOB是边长为4cm的等边三角形,求平行四边形ABCD的面积?
(
A
D
C
B
O
)
2、以△ABC的边AB、AC为边作等边△ABD和等边△ACE,且四边形ADFE是平行四边形。(1)当∠BAC等于 时,四边形ADFE是矩形;
(2)当∠BAC等于 时,平行四边形ADFE不存在;
(3)当△ABC满足什么条件时,平行四边形ADFE是菱形?
(4)当△ABC满足什么条件时,平行四边形ADFE是正方形?
六、【课后反思】
班级 : 组别: 组名: 姓名:
【学习目标】
1、掌握平行四边形、矩形、菱形、正方形的概念、性质和判定,并能灵活运用其进行有关论证和计算
2、理解平行四边形、矩形、菱形、正方形的区别与联系
【重点难点】
重点:平行四边形知识体系的结构化整理
难点:平行四边形知识的选择性应用
【学法指导】小组合作、分组展示
【知识链接】平行四边形、矩形、菱形、正方形的概念、性质和判定
【学习过程】
一、【自学】请阅读课本P66的内容,尝试完成以下问题:
知识点一:平行四边形的知识结构图
问题1:完成平行四边形知识结构定义图
问题2:完成平行四边形关系图
知识点二:平行四边形、矩形、菱形、正方形的性质
四边形 边 角 对 角 线 对称性
平行四边形
矩形
菱形
正方形
知识点三:平行四边形、矩形、菱形、正方形的判定方法
四边形 判 定 方 法
平行四边形
矩 形
菱 形
正 方 形
二、【知识应用】
知识点四:三角形中位线的性质
(
A
B
C
D
E
F
G
O
)1、如图,在△ABC中,中线BD、CE相交于点O,F、G分别是OB、OC的中点,
求证:四边形DEFG是平行四边形。
知识点五:我们把顺次连接任意一个四边形各边中点所得的四边形叫做中点四边形。
2、如图,在任意四边形ABCD中,E、F、G、H分别是边AB、BC、CD、DA的中点,
请判断四边形EFGH的形状,并证明。
知识点六:直角三角形斜边上的中线
3、如图,BD、CE是△ABC的高,G、F分别是BC、DE的中点,
求证:FG⊥DE。(连接EG、DG)
三、【基础达标】
1、Rt△OAB的两条直角边在坐标轴上,已知点A(2,0),点B(0,3),则以点O,A,B为其中三个顶点的平行四边形的第四个顶点C的坐标为__________ _。
(
A
B
C
E
F
G
D
)2、如图,把两个大小完全相同的矩形拼成“L”型图案,
则∠FAC= , ∠FCA= 。
3、矩形的一条角平分线分矩形的一边为1和3两部分,则这个矩形的面积为 。
4、菱形的面积是24cm2,一条对角线长为6cm,则菱形的高为 。
知识点七:菱形面积的2种求法:(1) (2) 。
(
A
C
D
B
P
E
F
)5、如图,P在正方形ABCD的对角线BD上一个动点,且PE⊥BC于E,PF⊥CD于F,AB=5cm,则四边形PECF的周长是 。
四、【课堂小结】
知识小结:
方法小结:
五、【当堂检测】
1、如图,在平行四边形ABCD中,两对角线AC、BD相交于点O,且△AOB是边长为4cm的等边三角形,求平行四边形ABCD的面积?
(
A
D
C
B
O
)
2、以△ABC的边AB、AC为边作等边△ABD和等边△ACE,且四边形ADFE是平行四边形。(1)当∠BAC等于 时,四边形ADFE是矩形;
(2)当∠BAC等于 时,平行四边形ADFE不存在;
(3)当△ABC满足什么条件时,平行四边形ADFE是菱形?
(4)当△ABC满足什么条件时,平行四边形ADFE是正方形?
六、【课后反思】
