人教版8年级下册数学《第十八章 平行四边形》单元测试(含答案)
文档属性
| 名称 | 人教版8年级下册数学《第十八章 平行四边形》单元测试(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-27 13:23:21 | ||
图片预览


文档简介
人教版数学八年级下册
《第十八章 平行四边形》单元测试卷
分值:120分 时间:90分钟
一、选择题(本大题共12道小题,共36分)
A.,1.矩形、菱形、正方形都有的性质是
A.对角线相等 B.对角线互相平分
C.对角线互相垂直 D.对角线平分一组对角
2.如图,平行四边形的对角线和相交于点,与面积相等的三角形的个数是
A. B. C. D.
(2) (3)
3.如图,在平行四边形中,若,,对角线,相交于点,则长的取值范围是
A. B.
C. D.
4.已知四边形是平行四边形,,相交于点,下列结论错误的是
B.当时,四边形是菱形
C.当时,四边形是矩形
D.当且时,四边形是正方形
5.如图,在 中,对角线与相交于点,是边的中点,连结若,,则的度数为
A. B. C. D.
(5) (6)
6.如图,是 内任一点,若,则图中阴影部分的面积是
A. B. C. D.
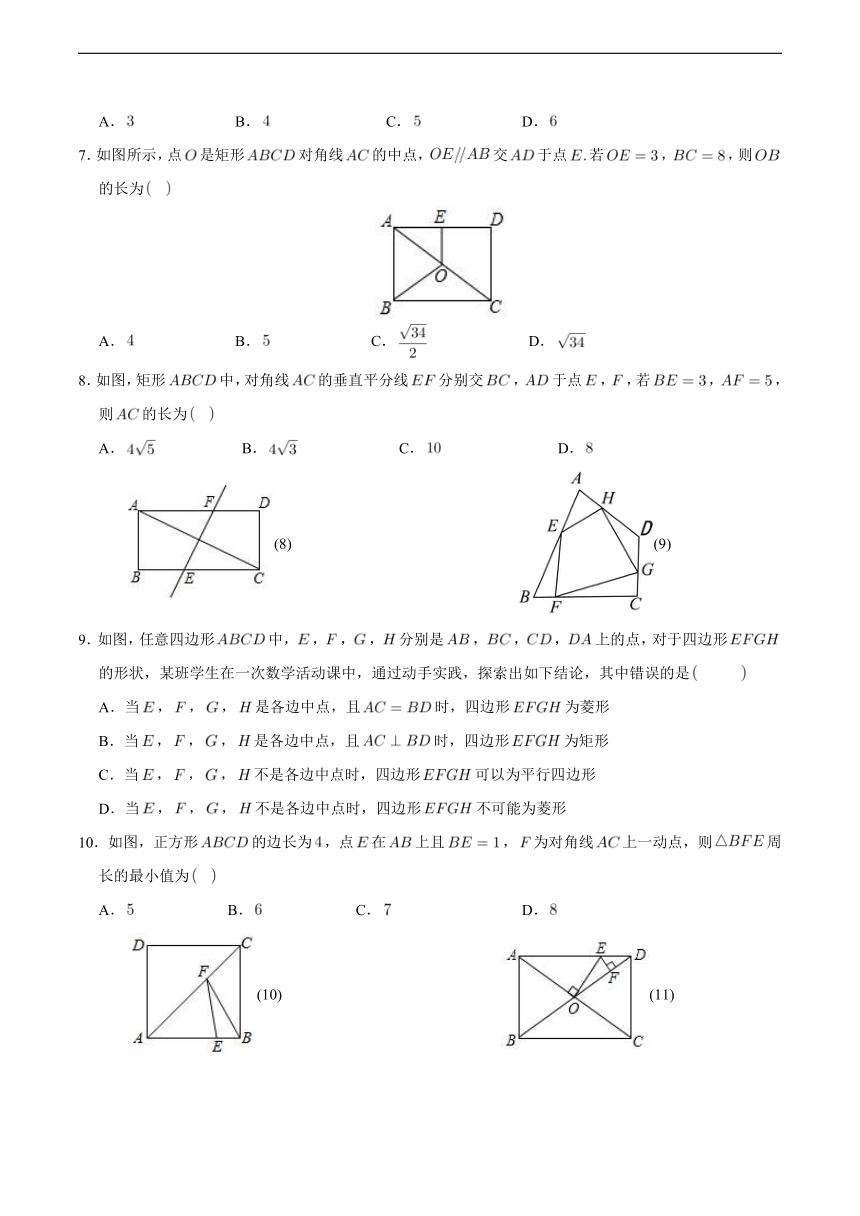
7.如图所示,点是矩形对角线的中点,交于点若,,则的长为
A. B. C. D.
8.如图,矩形中,对角线的垂直平分线分别交,于点,,若,,则的长为
A. B. C. D.
(8) (9)
9.如图,任意四边形中,,,,分别是,,,上的点,对于四边形的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是
A.当,,,是各边中点,且时,四边形为菱形
B.当,,,是各边中点,且时,四边形为矩形
C.当,,,不是各边中点时,四边形可以为平行四边形
D.当,,,不是各边中点时,四边形不可能为菱形
10.如图,正方形的边长为,点在上且,为对角线上一动点,则周长的最小值为
A. B. C. D.
(10) (11)
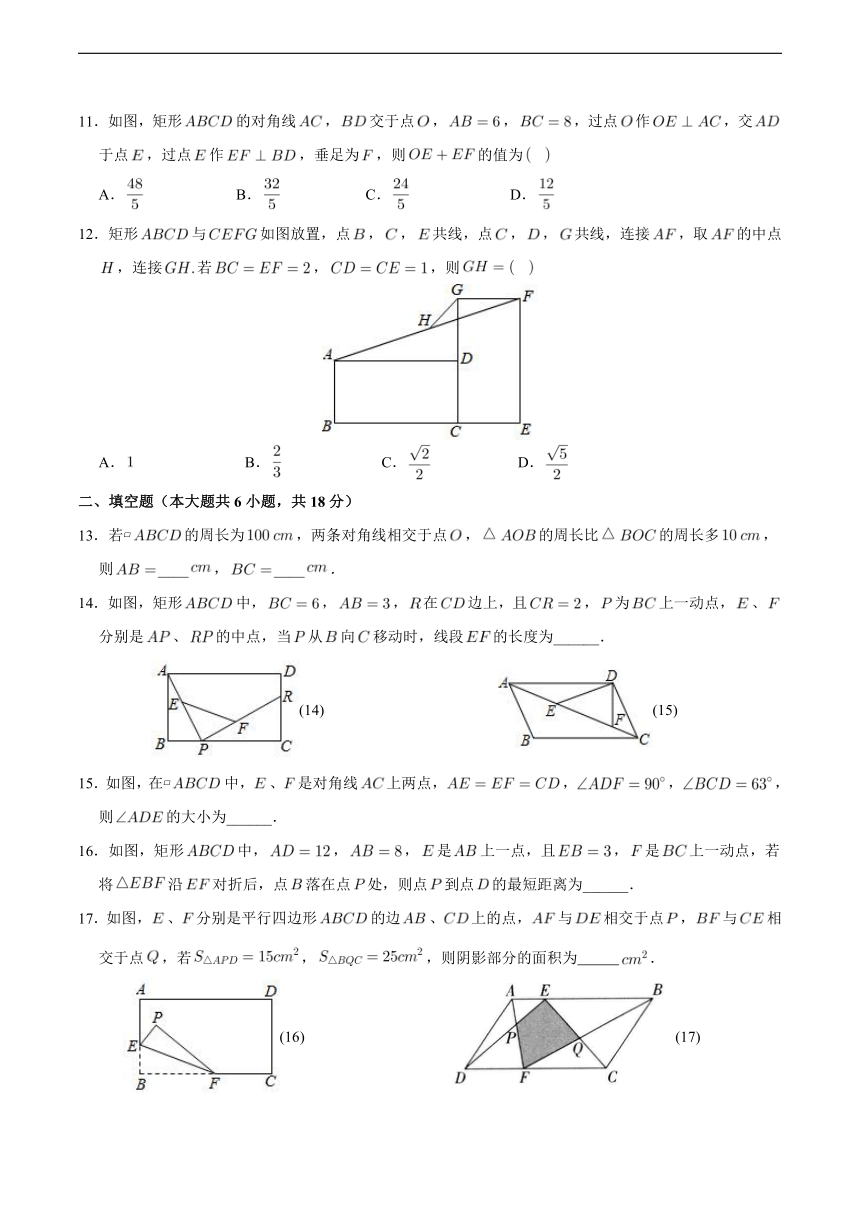
11.如图,矩形的对角线,交于点,,,过点作,交于点,过点作,垂足为,则的值为
A. B. C. D.
12.矩形与如图放置,点,,共线,点,,共线,连接,取的中点,连接若,,则
A. B. C. D.
二、填空题(本大题共6小题,共18分)
13.若 的周长为,两条对角线相交于点,的周长比的周长多,则____,____.
14.如图,矩形中,,,在边上,且,为上一动点,、分别是、的中点,当从向移动时,线段的长度为______.
(14) (15)
15.如图,在 中,、是对角线上两点,,,,则的大小为______.
16.如图,矩形中,,,是上一点,且,是上一动点,若将沿对折后,点落在点处,则点到点的最短距离为______.
17.如图,、分别是平行四边形的边、上的点,与相交于点,与相交于点,若,,则阴影部分的面积为 .
(16) (17)
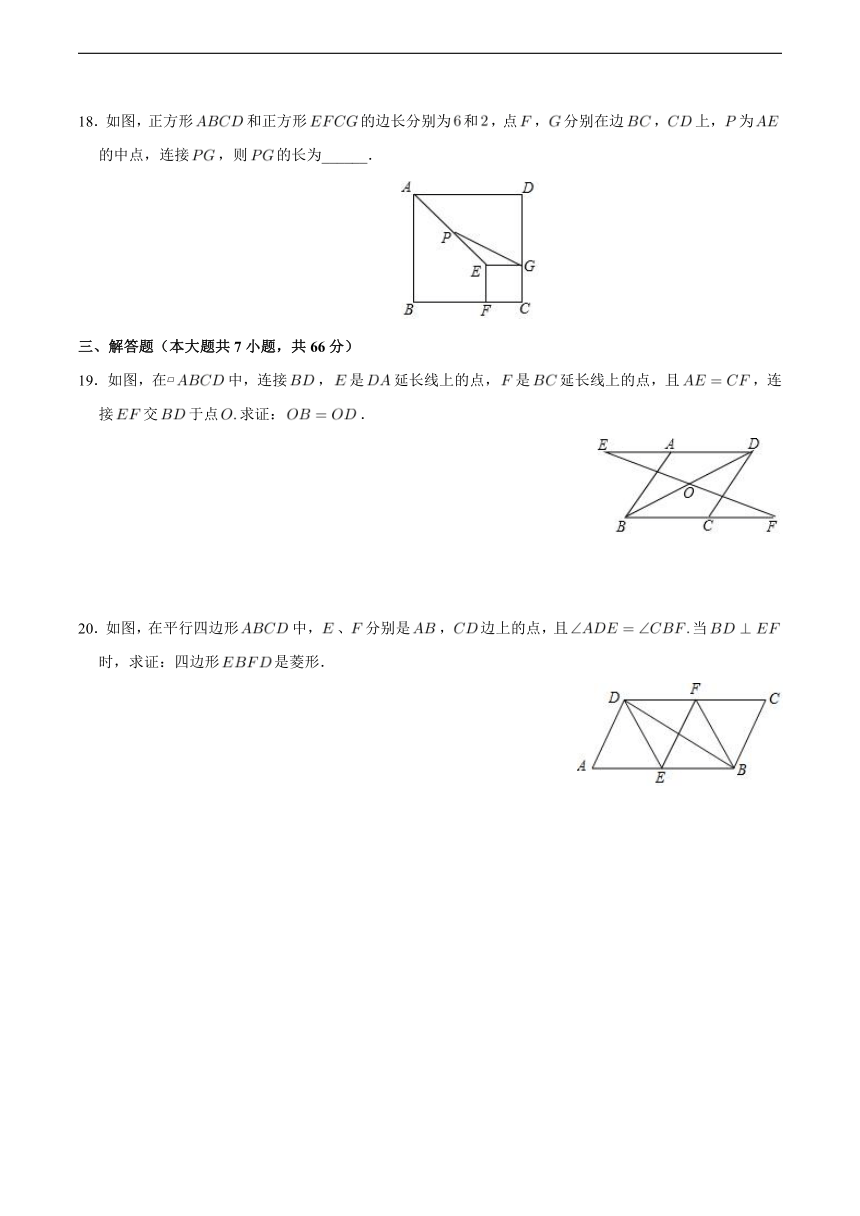
18.如图,正方形和正方形的边长分别为和,点,分别在边,上,为的中点,连接,则的长为______.
三、解答题(本大题共7小题,共66分)
19.如图,在 中,连接,是延长线上的点,是延长线上的点,且,连接交于点求证:.
20.如图,在平行四边形中,、分别是,边上的点,且当时,求证:四边形是菱形.
21.已知:如图,四边形是平行四边形,延长至点,使,连接、、,与交于点.
求证:四边形是平行四边形;
若求证:四边形是矩形.
22.如图,在 中,以点为圆心,长为半径画弧交于点,再分别以点、为圆心,大于的相同长为半径画弧,两弧交于点;连接并延长交于点,连接,则所得四边形是菱形.
根据以上尺规作图的过程,求证:四边形是菱形;
若菱形的周长为,,求的大小.
23.如图,点在 内部,,.
求证:≌;
设 的面积为,四边形的面积为,求的值.
24.如图,在中,是边上的一个动点,过点作直线,交的平分线于点,交的外角的平分线于点.
求证:
若,,求的长
连接,,当点在边上运动到什么位置时,四边形是矩形请说明理由.
25.如图,在四边形中,,,,,,点从点出发,以的速度向点运动点从点同时出发,以的速度向点运动规定其中一个动点到达端点时,另一个动点也随之停止运动设点,运动的时间为.
边的长度为 ,的取值范围为 .
从运动开始,当取何值时,
从运动开始,当取何值时,
在整个运动过程中是否存在值,使得四边形是菱形若存在,请求出值若不存在,请说明理由.
答案和解析
选择题(本大题共12道小题,共36分)
1-12
二、填空题(本大题共6小题,共18分)
13.;
14.
15.
16.
17.
18.
三、解答题(本大题共7小题,共66分)
19.证明: 中,,..
又,..
又,≌..
20.证明:四边形是平行四边形,
,,,,
在和中,,
≌,,
,即,
又,四边形是平行四边形,
,四边形是菱形.
21.证明: 中,且,
又,,,
四边形是平行四边形;
中,,,
又,,
,,
又平行四边形中,,
,
平行四边形是矩形.
22.解:在和中,
,≌,,
,,.
,四边形是平行四边形,
,四边形是菱形;
如图,连结,交于.
菱形的周长为,,
,,,.
在直角中,,,
.
四边形是平行四边形,.
23.解:四边形是平行四边形,
,,,
,,,同理得,
在和中,
,≌;
点在 内部,,
由知:≌,,
,
的面积为,四边形的面积为,.
24.证明:如图所示,
交的平分线于点,交的外角平分线于点,
,,
, ,, ,,
,, ;
解:,, ,
,,
, ;
解:当点在边上运动到中点时,四边形是矩形.
理由如下:当为的中点时,,
, 四边形是平行四边形,
, 平行四边形是矩形.
25.解:;;
,
当时,四边形为平行四边形,,
,,,,
当时;
由得当时四边形为平行四边形,此时,
当,运动到如图的位置时,
过点作于点,过点作于点,
则,
,
在和中≌,,
由得
,,,
综上所述,当的值为或时,;
不存在理由如下:
要使四边形为菱形,则四边形一定是平行四边形,
由得当时四边形是平行四边形,
此时,即,
四边形不是菱形,
所以不存在的值使四边形为菱形.
《第十八章 平行四边形》单元测试卷
分值:120分 时间:90分钟
一、选择题(本大题共12道小题,共36分)
A.,1.矩形、菱形、正方形都有的性质是
A.对角线相等 B.对角线互相平分
C.对角线互相垂直 D.对角线平分一组对角
2.如图,平行四边形的对角线和相交于点,与面积相等的三角形的个数是
A. B. C. D.
(2) (3)
3.如图,在平行四边形中,若,,对角线,相交于点,则长的取值范围是
A. B.
C. D.
4.已知四边形是平行四边形,,相交于点,下列结论错误的是
B.当时,四边形是菱形
C.当时,四边形是矩形
D.当且时,四边形是正方形
5.如图,在 中,对角线与相交于点,是边的中点,连结若,,则的度数为
A. B. C. D.
(5) (6)
6.如图,是 内任一点,若,则图中阴影部分的面积是
A. B. C. D.
7.如图所示,点是矩形对角线的中点,交于点若,,则的长为
A. B. C. D.
8.如图,矩形中,对角线的垂直平分线分别交,于点,,若,,则的长为
A. B. C. D.
(8) (9)
9.如图,任意四边形中,,,,分别是,,,上的点,对于四边形的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是
A.当,,,是各边中点,且时,四边形为菱形
B.当,,,是各边中点,且时,四边形为矩形
C.当,,,不是各边中点时,四边形可以为平行四边形
D.当,,,不是各边中点时,四边形不可能为菱形
10.如图,正方形的边长为,点在上且,为对角线上一动点,则周长的最小值为
A. B. C. D.
(10) (11)
11.如图,矩形的对角线,交于点,,,过点作,交于点,过点作,垂足为,则的值为
A. B. C. D.
12.矩形与如图放置,点,,共线,点,,共线,连接,取的中点,连接若,,则
A. B. C. D.
二、填空题(本大题共6小题,共18分)
13.若 的周长为,两条对角线相交于点,的周长比的周长多,则____,____.
14.如图,矩形中,,,在边上,且,为上一动点,、分别是、的中点,当从向移动时,线段的长度为______.
(14) (15)
15.如图,在 中,、是对角线上两点,,,,则的大小为______.
16.如图,矩形中,,,是上一点,且,是上一动点,若将沿对折后,点落在点处,则点到点的最短距离为______.
17.如图,、分别是平行四边形的边、上的点,与相交于点,与相交于点,若,,则阴影部分的面积为 .
(16) (17)
18.如图,正方形和正方形的边长分别为和,点,分别在边,上,为的中点,连接,则的长为______.
三、解答题(本大题共7小题,共66分)
19.如图,在 中,连接,是延长线上的点,是延长线上的点,且,连接交于点求证:.
20.如图,在平行四边形中,、分别是,边上的点,且当时,求证:四边形是菱形.
21.已知:如图,四边形是平行四边形,延长至点,使,连接、、,与交于点.
求证:四边形是平行四边形;
若求证:四边形是矩形.
22.如图,在 中,以点为圆心,长为半径画弧交于点,再分别以点、为圆心,大于的相同长为半径画弧,两弧交于点;连接并延长交于点,连接,则所得四边形是菱形.
根据以上尺规作图的过程,求证:四边形是菱形;
若菱形的周长为,,求的大小.
23.如图,点在 内部,,.
求证:≌;
设 的面积为,四边形的面积为,求的值.
24.如图,在中,是边上的一个动点,过点作直线,交的平分线于点,交的外角的平分线于点.
求证:
若,,求的长
连接,,当点在边上运动到什么位置时,四边形是矩形请说明理由.
25.如图,在四边形中,,,,,,点从点出发,以的速度向点运动点从点同时出发,以的速度向点运动规定其中一个动点到达端点时,另一个动点也随之停止运动设点,运动的时间为.
边的长度为 ,的取值范围为 .
从运动开始,当取何值时,
从运动开始,当取何值时,
在整个运动过程中是否存在值,使得四边形是菱形若存在,请求出值若不存在,请说明理由.
答案和解析
选择题(本大题共12道小题,共36分)
1-12
二、填空题(本大题共6小题,共18分)
13.;
14.
15.
16.
17.
18.
三、解答题(本大题共7小题,共66分)
19.证明: 中,,..
又,..
又,≌..
20.证明:四边形是平行四边形,
,,,,
在和中,,
≌,,
,即,
又,四边形是平行四边形,
,四边形是菱形.
21.证明: 中,且,
又,,,
四边形是平行四边形;
中,,,
又,,
,,
又平行四边形中,,
,
平行四边形是矩形.
22.解:在和中,
,≌,,
,,.
,四边形是平行四边形,
,四边形是菱形;
如图,连结,交于.
菱形的周长为,,
,,,.
在直角中,,,
.
四边形是平行四边形,.
23.解:四边形是平行四边形,
,,,
,,,同理得,
在和中,
,≌;
点在 内部,,
由知:≌,,
,
的面积为,四边形的面积为,.
24.证明:如图所示,
交的平分线于点,交的外角平分线于点,
,,
, ,, ,,
,, ;
解:,, ,
,,
, ;
解:当点在边上运动到中点时,四边形是矩形.
理由如下:当为的中点时,,
, 四边形是平行四边形,
, 平行四边形是矩形.
25.解:;;
,
当时,四边形为平行四边形,,
,,,,
当时;
由得当时四边形为平行四边形,此时,
当,运动到如图的位置时,
过点作于点,过点作于点,
则,
,
在和中≌,,
由得
,,,
综上所述,当的值为或时,;
不存在理由如下:
要使四边形为菱形,则四边形一定是平行四边形,
由得当时四边形是平行四边形,
此时,即,
四边形不是菱形,
所以不存在的值使四边形为菱形.
