第8章 数学广角数与形人教版小学六年级数学上册单元测试题(解析版)
文档属性
| 名称 | 第8章 数学广角数与形人教版小学六年级数学上册单元测试题(解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 242.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-26 15:08:35 | ||
图片预览


文档简介
人教版小学六年级数学上册 第8章 数学广角-数与形 单元测试题
一.选择题(共8小题)
1.5÷7的商用循环小数表示,这个小数的小数点后面第150位数字是( )
A.1 B.2 C.5 D.7
2.如图,按这样的规律第7个图形有( )个点.
A.21 B.25 C.28 D.29
3.一组有规律的数:1.1,1.2,1.3,1.4,1.5,□,1.7……框里的数是( )
A.0.5 B.1.5 C.0.6 D.1.6
4.同学们你们知道吗,在阿拉伯数字传入中国之前,我们的祖先也发明了记录数字的符号(如图),他们用横纵相间的方式来表示一个数.如:表示的是28.那:表示的是( )
A.211 B.226 C.271 D.276
5.某种细胞开始有2个,一小时后分裂成4个并死去1个,二小时分裂成6个并死去1个,三小时后分裂成10个并死去1个,按此规律,五小时后细胞存活的个数是( )
A.31 B.33 C.35 D.37
6.9,18,27,( ),45.
A.66 B.36 C.55
7.将一些半径相同的小圆按如图所示的规律摆放:第1个图形有6个小圆,第2个图形有10个小圆,第3个图形有16个小圆,第4个图形有24个小圆…依此规律,第10个图形中小圆的个数为( )
A.136 B.114 C.112 D.106
8.11÷9=1.222…,21÷9=2.333…,31÷9=3.444…,则算式61÷9的商是( )
A.4.555… B.5.666… C.6.777… D.7.888…
二.填空题(共8小题)
9.甲、乙两人在楼梯上玩石头剪子布的游戏,每次必须分出胜负.约定:每次胜者上5个台阶,负者下3个台阶.甲、乙二人同时在第50个台阶上开始玩,玩了25次后,甲的位置比乙高40个台阶.那么,甲胜了 次.
10.找规律.
(1)2,12,22, , , .
(2)95,75,55, , .
11.观察算式37×3=111,37×6=222,那么37×9= ,37×21= .
12.找出下列算式的规律,并根据规律把算式填写完整.
1×8+1=9
12×8+2=98
123×8+3=987
1234×8+4=9876
……
×8+9=
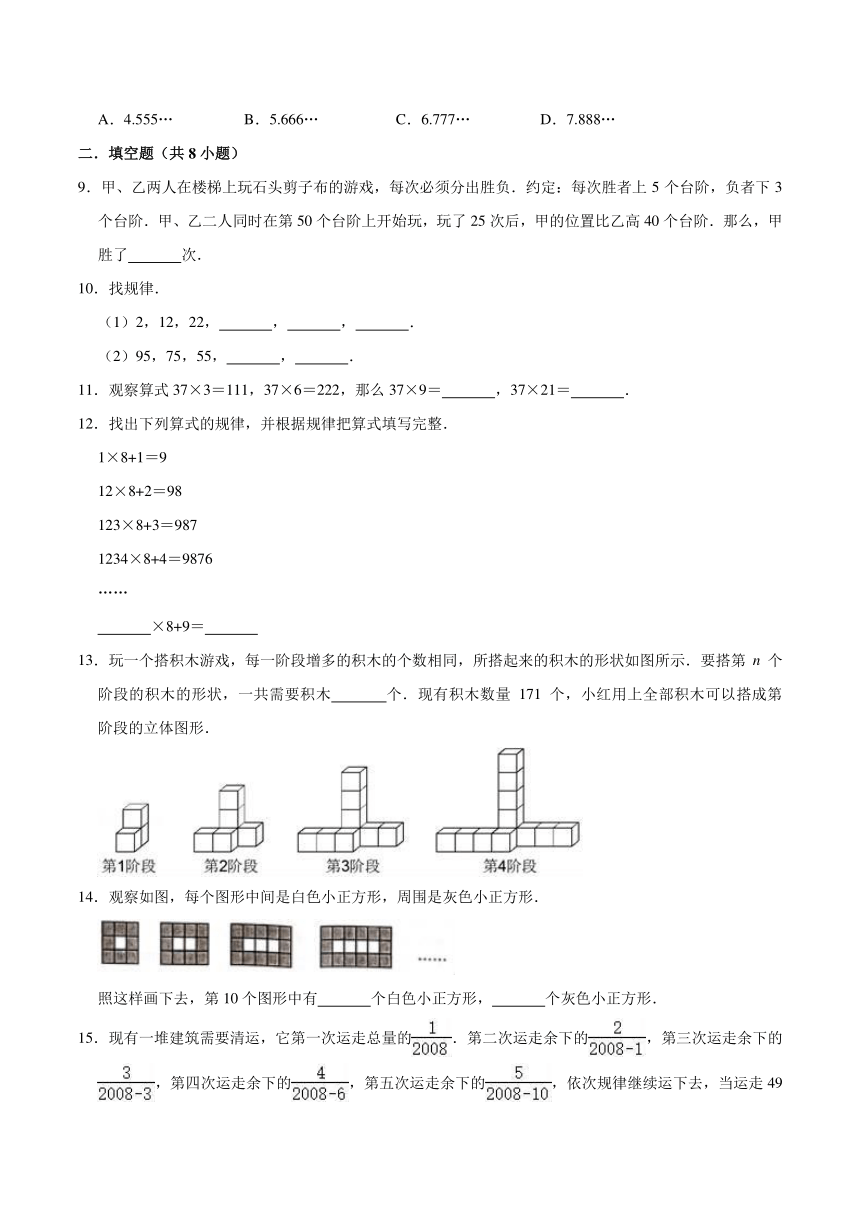
13.玩一个搭积木游戏,每一阶段增多的积木的个数相同,所搭起来的积木的形状如图所示.要搭第n个阶段的积木的形状,一共需要积木 个.现有积木数量171个,小红用上全部积木可以搭成第 阶段的立体图形.
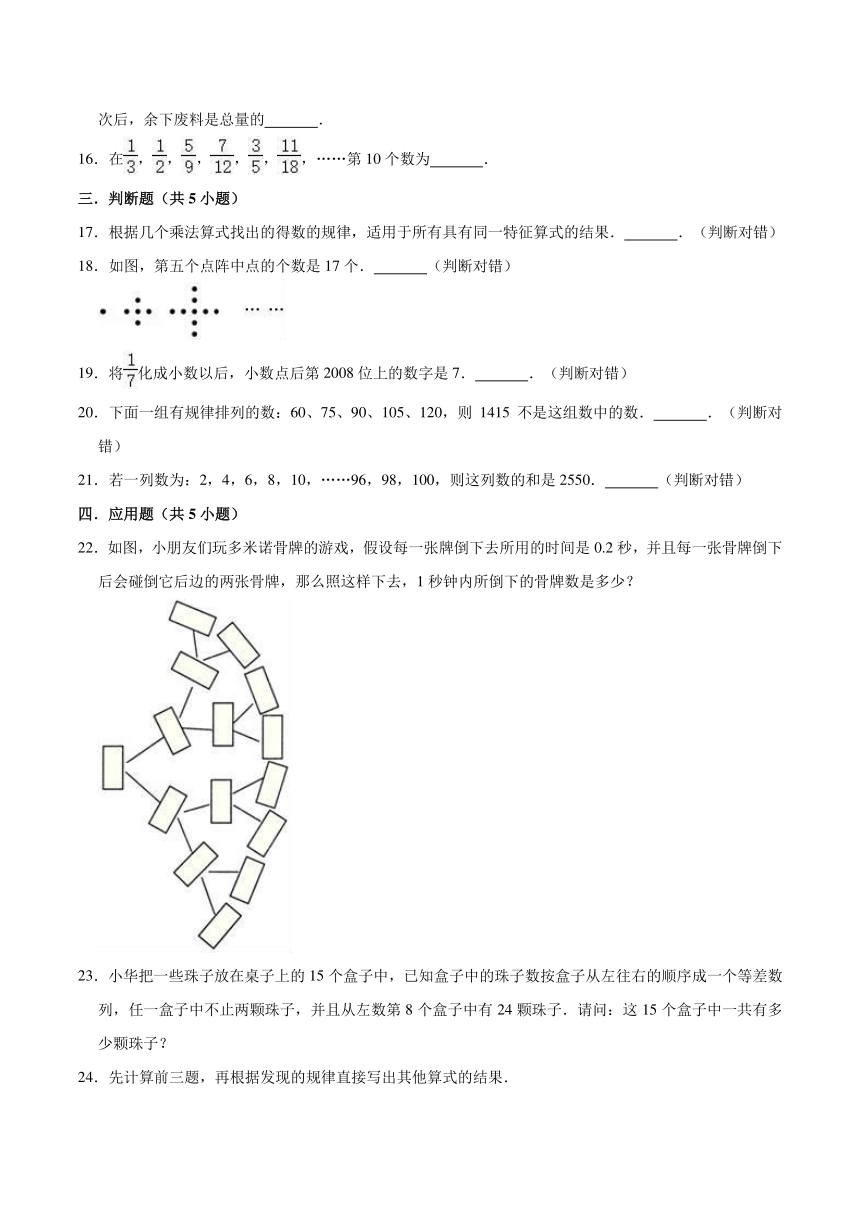
14.观察如图,每个图形中间是白色小正方形,周围是灰色小正方形.
照这样画下去,第10个图形中有 个白色小正方形, 个灰色小正方形.
15.现有一堆建筑需要清运,它第一次运走总量的.第二次运走余下的,第三次运走余下的,第四次运走余下的,第五次运走余下的,依次规律继续运下去,当运走49次后,余下废料是总量的 .
16.在,,,,,,……第10个数为 .
三.判断题(共5小题)
17.根据几个乘法算式找出的得数的规律,适用于所有具有同一特征算式的结果. .(判断对错)
18.如图,第五个点阵中点的个数是17个. (判断对错)
19.将化成小数以后,小数点后第2008位上的数字是7. .(判断对错)
20.下面一组有规律排列的数:60、75、90、105、120,则1415不是这组数中的数. .(判断对错)
21.若一列数为:2,4,6,8,10,……96,98,100,则这列数的和是2550. (判断对错)
四.应用题(共5小题)
22.如图,小朋友们玩多米诺骨牌的游戏,假设每一张牌倒下去所用的时间是0.2秒,并且每一张骨牌倒下后会碰倒它后边的两张骨牌,那么照这样下去,1秒钟内所倒下的骨牌数是多少?
23.小华把一些珠子放在桌子上的15个盒子中,已知盒子中的珠子数按盒子从左往右的顺序成一个等差数列,任一盒子中不止两颗珠子,并且从左数第8个盒子中有24颗珠子.请问:这15个盒子中一共有多少颗珠子?
24.先计算前三题,再根据发现的规律直接写出其他算式的结果.
1+3═ =22
1+3+5═ =32
1+3+5+7═ =
…
1+3+5+7+…+15═ =
1+3+5+7+…+2017= =
25.用6根同样长的小棒可以摆成一个正六边形(如图①),再接着摆下去(如图②、③、④),图⑧一共需要多少根小棒?
26.如图,第二个图形是由第一个图形连接三边中点而得到的,第三个图形是由第二个图形中间的一个三角形连接三边中点而得到的,以此类推……分别写出第二个图形、第三个图形和第四个图形中的三角形个数.如果第n个图形中的三角形个数为8057,n是多少?
五.操作题(共2小题)
27.根据下面几幅图的规律,接着怎么画?
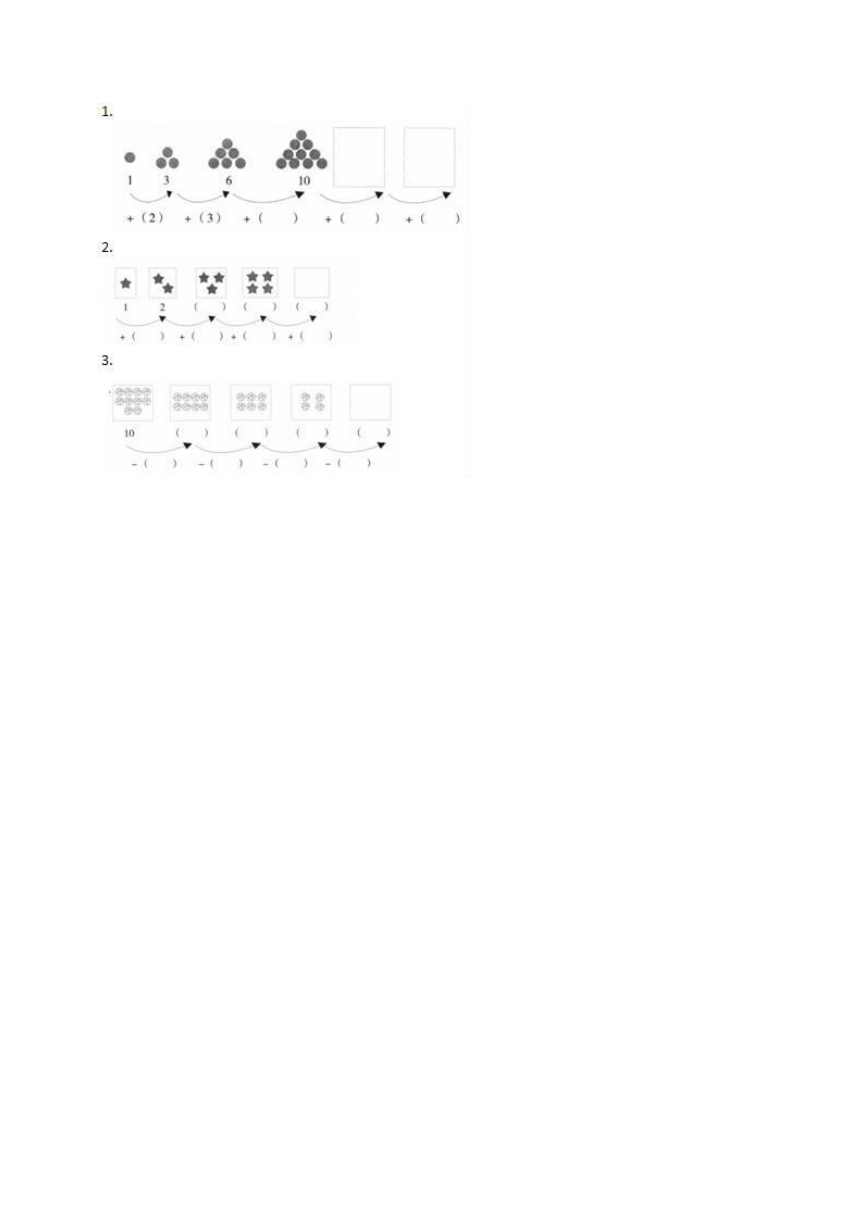
28.先找规律,再认真画规律.
参考答案与试题解析
一.选择题(共8小题)
1.【分析】把5÷7=0.,这个小数的循环节是714285,有6位数,150÷6=25(个,所以小数部分的第150位数字是25的最后一个数字是5,据此解答.
【解答】解:5÷7=0.,
循环节是714285六个数字;
150÷6=25(个),
所以第150位数字是第25个循环节的最后一个数字,是5.
故选:C.
【点评】解题的关键是找出循环节及循环节的数字,用150除以循环节的位数得出是第几个循环节,没有余数就是循环节的最后一个数字,有余数的,余数是几就是循环节的第几个数字.
2.【分析】认真观察图示,第1个图形点数是1,第2个图形点数是5,第3个图形点数是9,发现:相邻两个图形的点数相差是4,据此求出即可.
【解答】解:第1个图形点数是1,
第2个图形点数是5,
第3个图形点数是9,则:
第4个图形点数是:9+4=13,
第5个图形点数是:13+4=17,
第6个图形点数是:17+4=21,
第7个图形点数是:21+4=25.
故选:B.
【点评】认真观察图画,得出点数的规律是解题关键.
3.【分析】根据已知的6个数可得排列规律:从第1项开始每次递增0.1;据此解答.
【解答】解:1.5+0.1=1.6
故选:D.
【点评】数列中的规律:关键是根据已知的式子或数得出前后算式或前后数之间的变化关系和规律,然后再利用这个变化规律再回到问题中去解决问题.
4.【分析】根据纵式与横式表示数的规律,百位上两竖表示2;十位上一竖下面两横,表示7;个位一横下面一竖表示6.所以表示276.
【解答】解:表示276.
故选:D.
【点评】本题主要考查数与形结合的规律,关键根据所给图形发现规律,并运用规律做题.
5.【分析】由题意可知,1个活细胞一小时后分裂成2个.1小时后3个活的、2小时后5个活的、3小时后9个活的……3、5、9……可看作项数为1、2、3……首项为3差分别为1、4、8……的数列.5﹣3=2=21、9﹣5=4=22、17﹣9=8=23……由此可以推出:第n项为2n+1.
【解答】解:由分析所总结的规律:
25+1
=32+1
=33(个)
答:五小时后细胞存活的个数是33个.
故选:B.
【点评】解答此题的关键是根据小时数(可看作项数),与分成成的活细胞(可看作项)之间的关系找出规律,然后根据规律可求出任何小时(整数)后活细胞的个数.
6.【分析】18﹣9=9,27﹣18=9,推测规律为:后一个数等于前一个数加9,以此计算,得出结果后,验证得数和其后面的数是否符合规律.
【解答】解:由分析可知:第四项为27+9=36
45﹣36=9
所以,找到的规律是正确的.
故选:B.
【点评】本题主要考查了数列中的规律,需要学生具有较好的数感和推理能力.
7.【分析】分析数据可得:第1个图形中小圆的个数为6;第2个图形中小圆的个数为10;第3个图形中小圆的个数为16;第4个图形中小圆的个数为24;则知第n个图形中小圆的个数为n(n+1)+4;由此把n=10代入计算即可.
【解答】解:10×11+4
=110+4
=114(个)
答:第10个图形中小圆的个数为114个.
故选:B.
【点评】本题是一道找规律的题目,这类题型在中考中经常出现.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,得出通项公式,从而解决问题.
8.【分析】观察已知的三个算式,可以发现,商的整数部分等于被除数的十位数字,小数循环部分的循环节是被除数十位上数字加1,以此作答.
【解答】解:由分析可知:61÷9的商,整数部分为6,小数循环节为6+1=7,
所以,61÷9=6.7777……
故选:C.
【点评】本题主要考查了“式”的规律,需要学生具有较好的数感.
二.填空题(共8小题)
9.【分析】根据题意,每次二人相差3+5=8(个)台阶,甲比乙高40个台阶,说明甲比乙多赢40÷8=5(次),其余次数二人输赢一样多.据此解答即可.
【解答】解:[25+40÷(5+3)]÷2
=[25+40÷8]÷2
=[25+5]÷2
=30÷2
=15(次)
答:甲胜了15次.
故答案为:15.
【点评】本题主要考查算术中的规律,关键根据题意找出二人每次胜负的台阶差.
10.【分析】(1)根据每次增加10求解;
(2)根据每次减少20求解.
【解答】解:(1)2,12,22,32,42,52.
(2)95,75,55,35,15.
故答案为:32,42,52;35,15.
【点评】通过观察,分析、归纳并发现其中的规律,并应用发现的规律解决问题是应该具备的基本能力.
11.【分析】根据积的变化规律:一个因数不变,另一个因数扩大或缩小多少倍(0除外),积也会随着扩大或缩小相同的倍数,据此解答即可得到答案.
【解答】解:因为
37×3=111
37×6=222
所以
37×9=333,
37×21=37×3×7=777,
故答案为:333,777.
【点评】此题主要考查的是积的变化规律的灵活应用,关键是根据已知算式找到规律.
12.【分析】从以上几题可以看出,用自然数从一位数开始,按从小到大自然数的顺序组成不同位数的数乘以8再加前面数的个位数,发现几位与8相乘结果还是几位,只是数从高位从大到小按自然数顺序排列,根据此规律就可填出得数.
【解答】解:1×8+1=9
12×8+2=98
123×8+3=987
1234×8+4=9876
……
123456789×8+9=987654321
故答案为:123456789,987654321.
【点评】解答本题的关键是根据已知数据找出规律,然后利用规律解题.
13.【分析】根据所给图示发现:这组积木的排列规律:第1个阶段积木个数:3×1=3(个);第2个阶段积木个数:3×2=6(个);第3个阶段积木个数:3×3=9(个)……第n个阶段积木个数为:3×n=3n(个).据此解答.
【解答】解:第1个阶段积木个数:3×1=3(个)
第2个阶段积木个数:3×2=6(个)
第3个阶段积木个数:3×3=9(个)
……
第n个阶段积木个数为:3×n=3n(个)
3n=171
n=57
答:要搭第n个阶段的积木的形状,一共需要积木3n个.现有积木数量171个,小红用上全部积木可以搭成第57阶段的立体图形.
故答案为:3n;57.
【点评】本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力.
14.【分析】根据所给图示可知:这组图形的排列规律:第一个图形白色小正方形的个数为1个,灰色小正方形的个数为6+2=8(个);第二个图形白色小正方形的个数为:2个,灰色小正方形的个数为:6+2+2=10(个);……第n个图形的白色小正方形的个数为n个,灰色小正方形的个数为(6+2n)个.据此解答.
【解答】解:第一个图形白色小正方形的个数为1个,灰色小正方形的个数为6+2=8(个)
第二个图形白色小正方形的个数为:2个,灰色小正方形的个数为:6+2+2=10(个)
……
第n个图形的白色小正方形的个数为n个,灰色小正方形的个数为(6+2n)个
所以第10个图形白色小正方形的个数为:10个
灰色小正方形的个数为:6+2×10=26(个)
答:第10个图形中有10个白色小正方形,26个灰色小正方形.
故答案为:10;26.
【点评】本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力.
15.【分析】由题意,可得规律:它第一次运走总量的;第二次运走余下的,即总量的(1﹣)×=;第三次运走余下的,即总量的:()×=;……第n次运走总量的:;第49次运走总量的:,则最后剩下:1﹣()=1﹣=
据此解答.
【解答】解:它第一次运走总量的;
第二次运走余下的,即总量的(1﹣)×=;
第三次运走余下的,即总量的:()×=;
……
第n次运走总量的:;
……
第49次运走总量的:,
则最后剩下:
1﹣()
=1﹣
=
答:当运走49次后,余下废料是总量的.
故答案为:
【点评】本题主要考查算术中的规律,关键运用分数的意义做题.
16.【分析】观察各式的分母,3=1×3,9=3×3,12=4×3,18=6×3,推测分母为3的连续倍数,根据此规律,将化为,化为,再观察各式的分子,1、3、5、7、9、11,为连续奇数,以此推断第十个数.
【解答】解:由分析可知,第十个的数分母为10×3=30,分子为2×10﹣1=19,
所以,第10个数为.
故答案为:.
【点评】本题主要考查了数列中的规律,先观察出分母的规律,然后改写部分项,再找出分子的规律,是本题解题的关键.
三.判断题(共5小题)
17.【分析】根据几个乘法算式找出的得数的规律,适用于所有具有同一特征算式的结果.如1×9=9、12×9=108、123×9=1107…如果第一个因数是1、12、123、1234…第二个因数都是9,其积所有数位的数字之和等于9,个位分别是9、8、7、6…十位都是0,其余数位上都是1.
【解答】解:如
1×9=9
12×9=108
123×9=1107
…
根据几个乘法算式找出的得数的规律,适用于所有具有同一特征算式的结果,这种说法正确.
故答案为:√.
【点评】只要几个乘法算式变化有一定的规律,其积也有一定规律.根据找出的规律可以写出符合这一规律所有算式的积.
18.【分析】根据图示,发现这组图形的规律:第一个点阵中点的个数:1个;第二个点阵中点的个数:1+4=5(个);第三个点阵中点的个数:1+4+4=9(个);……第n个点阵中点的个数:1+4(n﹣1)=(4n﹣3)(个).据此判断即可.
【解答】解:第一个点阵中点的个数:1个
第二个点阵中点的个数:1+4=5(个)
第三个点阵中点的个数:1+4+4=9(个)
……
第n个点阵中点的个数:1+4(n﹣1)=(4n﹣3)(个)
……
第五个点阵中点的个数:
4×5﹣3
=20﹣3
=17(个)
答:第五个点阵中点的个数是17个.所以原说法正确.
故答案为:√.
【点评】本题主要考查数与形结合的规律,关键根据图示发现这组图形的规律,并运用规律做题.
19.【分析】把分数化成小数,就会发现小数点后的数字是有规律的:=0.142857142857…,一直重复142857,所以小数点后的数字周期为6,2008÷6=334…4,每个周期第四个数为8,所以小数点后第2008位上的数字是8.
【解答】解:=1÷7=0.142857142857…,
一直重复142857,所以小数点后的数字周期为6.
2008÷6=334…4,
故小数点后第2008位上的数字是8.
故答案为:×.
【点评】考查了小数与分数的互化,算术中的规律,本题的关键是得到转化为小数,找出数字循环周期为6.
20.【分析】这组数每次递增15,所以用1415减去60,看能否被15整除即,如果能整除就是,否则不是;据此解答.
【解答】解:75﹣60=15,90﹣75=15,…,
所以这组数每次递增15,
(1415﹣60)÷15≈90.33,
所以,1415不是这组数中的数.
故答案为:√.
【点评】此题考查了数列的规律,关键是求出每次递增的数.
21.【分析】求2,4,6,8,10,……96,98,100的和即为求:2+4+6+8+10+…+100=?n=50,根据等差数列的求和公式完成计算.
【解答】解:2+4+6+8+10+…+100
=
=
=2550
所以原题计算正确.
故答案为:√.
【点评】根据等差数列求和公式进行计算,找出等差数列的公差,首项,尾项和项数是计算的关键.
四.应用题(共5小题)
22.【分析】1÷0.2=5,即1秒里面有5个0.2秒.第一张倒下后过0.2秒(1个0.2秒)会倒下2张、再过0.2秒(2个0.2秒)后会倒下4张、再过0.2秒(3个0.2秒)后会倒下8张、再过0.2秒(4个0.2秒)会倒下16张、再过0.2秒(5个0.2秒)会倒下32张.1、2、4、8、16、32.是公比为2的等比递增数列.最后把这些张数相加.
【解答】解:1÷0.2=5,即1秒里面有5个0.2秒
倒下第1张后
第1个0.2秒后会倒下2张
第2个0.2秒后会倒下4张
第3个0.2秒后会倒下8张
第4个0.2秒后会倒下16张
第5个0.2秒后会倒下32张
1+2+4+8+16+32
=1+2+(4+16)+(8+32)
=1+2+20+40
=63(张)
答:1秒钟内所倒下的骨牌数是63张.
【点评】这个数列项数是有限的,可以求出每次倒下的张数,然后再把倒下的总张数相加.如果项数较多要找规律解答.用小学知识只能这样解答.
23.【分析】15个盒子中的珠子从左到右是一个项数为15的等差数列,其中第8个盒子中的珠子数为中间项,根据等差数列的意义,与中间项相邻的左、右两项之和等于中间项,与中间项相隔1项的左、右两项之和也等于中间项……因此,这15项之和就是等于中间项乘中间项数.
【解答】解:24×15=360(颗)
答:这15个盒子中一共有360颗珠子.
【点评】解答此题的关键是明白:与中间项相邻的左、右两项之和等于中间项,与中间项相隔1项的左、右两项之和也等于中间项……
24.【分析】1+3═4=22
1+3+5═9=32
1+3+5+7═16=42
…
规律:[(首数+尾数)÷2]2=和;据此解答即可.
【解答】解:1+3═4=22
1+3+5═9=32
1+3+5+7═16=42
…
1+3+5+7+…+15═64=82
1+3+5+7+…+2017=1016064=10082
故答案为:4,22,9,32,16,42,64,82,1016064,10082.
【点评】解答此题的关键是观察所给出的算式,找出算式之间数与数的关系,得出规律,再根据规律解决问题.
25.【分析】摆1个六边形需要6根小棒,可以写作:5×1+1;摆2个需要11根小棒,可以写作:5×2+1;摆3个需要16根小棒,可以写成:5×3+1;…由此可以推理得出一般规律解答问题.
【解答】解:根据题干分析可得:摆1个六边形需要6根小棒,可以写作:5×1+1;
摆2个需要11根小棒,可以写作:5×2+1;
摆3个需要小棒:5×3+1=16;
摆n个需要小棒:5×n+1=5n+1;
当n=8时,5n+1=5×8+1=41;
答:图⑧一共需要41根小棒.
【点评】根据题干中已知的图形的排列特点及其数量关系,推理得出一般的结论进行解答,是此类问题的关键.
26.【分析】根据图示,发现其规律为:第一个图形中三角形个数:1个;第二个图形中三角形个数:1×4+1=5(个);第三个图形中三角形个数:2×4+1=9(个);第四个图形中三角形个数:3×4+1=13(个);第n个图形中三角形个数:(n﹣1)×4+1=(4n﹣3)(个),计算n的值即可.
【解答】解:第一个图形中三角形个数:1个;
第二个图形中三角形个数:1×4+1=5(个);
第三个图形中三角形个数:2×4+1=9(个);
第四个图形中三角形个数:3×4+1=13(个);
第n个图形中三角形个数:
(n﹣1)×4+1=(4n﹣3)(个)
4n﹣3=8057,n=2015.
答:n是第2015个图形.
【点评】本题主要考查数与形结合的规律,关键根据所给图示发现图示排列的规律,并运用规律做题.
五.操作题(共2小题)
27.【分析】根据图形,第一个图:2个,第二个图:4个; 第三个图:6个……所以,这组图形的规律是:图形的个数是连续的偶数个.据此作图即可.
【解答】解:如图:
【点评】本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力.
28.【分析】(1)3﹣1=2,6﹣3=3,10﹣6=4,相邻两个数的差依次是2,3,4,……,依次增加1;
(2)观察图中的星星的个数,分别是1、2、3、4……依次增加1;
(3)观察图中图形的个数,分别是10,8,6,4,……,依次减少2;
由此求解.
【解答】解:1.
2.
3.
【点评】关键是根据已知的数得出前后图形、数之间的变化关系的规律,然后再利用这个变化规律再回到问题中去解决问题.
一.选择题(共8小题)
1.5÷7的商用循环小数表示,这个小数的小数点后面第150位数字是( )
A.1 B.2 C.5 D.7
2.如图,按这样的规律第7个图形有( )个点.
A.21 B.25 C.28 D.29
3.一组有规律的数:1.1,1.2,1.3,1.4,1.5,□,1.7……框里的数是( )
A.0.5 B.1.5 C.0.6 D.1.6
4.同学们你们知道吗,在阿拉伯数字传入中国之前,我们的祖先也发明了记录数字的符号(如图),他们用横纵相间的方式来表示一个数.如:表示的是28.那:表示的是( )
A.211 B.226 C.271 D.276
5.某种细胞开始有2个,一小时后分裂成4个并死去1个,二小时分裂成6个并死去1个,三小时后分裂成10个并死去1个,按此规律,五小时后细胞存活的个数是( )
A.31 B.33 C.35 D.37
6.9,18,27,( ),45.
A.66 B.36 C.55
7.将一些半径相同的小圆按如图所示的规律摆放:第1个图形有6个小圆,第2个图形有10个小圆,第3个图形有16个小圆,第4个图形有24个小圆…依此规律,第10个图形中小圆的个数为( )
A.136 B.114 C.112 D.106
8.11÷9=1.222…,21÷9=2.333…,31÷9=3.444…,则算式61÷9的商是( )
A.4.555… B.5.666… C.6.777… D.7.888…
二.填空题(共8小题)
9.甲、乙两人在楼梯上玩石头剪子布的游戏,每次必须分出胜负.约定:每次胜者上5个台阶,负者下3个台阶.甲、乙二人同时在第50个台阶上开始玩,玩了25次后,甲的位置比乙高40个台阶.那么,甲胜了 次.
10.找规律.
(1)2,12,22, , , .
(2)95,75,55, , .
11.观察算式37×3=111,37×6=222,那么37×9= ,37×21= .
12.找出下列算式的规律,并根据规律把算式填写完整.
1×8+1=9
12×8+2=98
123×8+3=987
1234×8+4=9876
……
×8+9=
13.玩一个搭积木游戏,每一阶段增多的积木的个数相同,所搭起来的积木的形状如图所示.要搭第n个阶段的积木的形状,一共需要积木 个.现有积木数量171个,小红用上全部积木可以搭成第 阶段的立体图形.
14.观察如图,每个图形中间是白色小正方形,周围是灰色小正方形.
照这样画下去,第10个图形中有 个白色小正方形, 个灰色小正方形.
15.现有一堆建筑需要清运,它第一次运走总量的.第二次运走余下的,第三次运走余下的,第四次运走余下的,第五次运走余下的,依次规律继续运下去,当运走49次后,余下废料是总量的 .
16.在,,,,,,……第10个数为 .
三.判断题(共5小题)
17.根据几个乘法算式找出的得数的规律,适用于所有具有同一特征算式的结果. .(判断对错)
18.如图,第五个点阵中点的个数是17个. (判断对错)
19.将化成小数以后,小数点后第2008位上的数字是7. .(判断对错)
20.下面一组有规律排列的数:60、75、90、105、120,则1415不是这组数中的数. .(判断对错)
21.若一列数为:2,4,6,8,10,……96,98,100,则这列数的和是2550. (判断对错)
四.应用题(共5小题)
22.如图,小朋友们玩多米诺骨牌的游戏,假设每一张牌倒下去所用的时间是0.2秒,并且每一张骨牌倒下后会碰倒它后边的两张骨牌,那么照这样下去,1秒钟内所倒下的骨牌数是多少?
23.小华把一些珠子放在桌子上的15个盒子中,已知盒子中的珠子数按盒子从左往右的顺序成一个等差数列,任一盒子中不止两颗珠子,并且从左数第8个盒子中有24颗珠子.请问:这15个盒子中一共有多少颗珠子?
24.先计算前三题,再根据发现的规律直接写出其他算式的结果.
1+3═ =22
1+3+5═ =32
1+3+5+7═ =
…
1+3+5+7+…+15═ =
1+3+5+7+…+2017= =
25.用6根同样长的小棒可以摆成一个正六边形(如图①),再接着摆下去(如图②、③、④),图⑧一共需要多少根小棒?
26.如图,第二个图形是由第一个图形连接三边中点而得到的,第三个图形是由第二个图形中间的一个三角形连接三边中点而得到的,以此类推……分别写出第二个图形、第三个图形和第四个图形中的三角形个数.如果第n个图形中的三角形个数为8057,n是多少?
五.操作题(共2小题)
27.根据下面几幅图的规律,接着怎么画?
28.先找规律,再认真画规律.
参考答案与试题解析
一.选择题(共8小题)
1.【分析】把5÷7=0.,这个小数的循环节是714285,有6位数,150÷6=25(个,所以小数部分的第150位数字是25的最后一个数字是5,据此解答.
【解答】解:5÷7=0.,
循环节是714285六个数字;
150÷6=25(个),
所以第150位数字是第25个循环节的最后一个数字,是5.
故选:C.
【点评】解题的关键是找出循环节及循环节的数字,用150除以循环节的位数得出是第几个循环节,没有余数就是循环节的最后一个数字,有余数的,余数是几就是循环节的第几个数字.
2.【分析】认真观察图示,第1个图形点数是1,第2个图形点数是5,第3个图形点数是9,发现:相邻两个图形的点数相差是4,据此求出即可.
【解答】解:第1个图形点数是1,
第2个图形点数是5,
第3个图形点数是9,则:
第4个图形点数是:9+4=13,
第5个图形点数是:13+4=17,
第6个图形点数是:17+4=21,
第7个图形点数是:21+4=25.
故选:B.
【点评】认真观察图画,得出点数的规律是解题关键.
3.【分析】根据已知的6个数可得排列规律:从第1项开始每次递增0.1;据此解答.
【解答】解:1.5+0.1=1.6
故选:D.
【点评】数列中的规律:关键是根据已知的式子或数得出前后算式或前后数之间的变化关系和规律,然后再利用这个变化规律再回到问题中去解决问题.
4.【分析】根据纵式与横式表示数的规律,百位上两竖表示2;十位上一竖下面两横,表示7;个位一横下面一竖表示6.所以表示276.
【解答】解:表示276.
故选:D.
【点评】本题主要考查数与形结合的规律,关键根据所给图形发现规律,并运用规律做题.
5.【分析】由题意可知,1个活细胞一小时后分裂成2个.1小时后3个活的、2小时后5个活的、3小时后9个活的……3、5、9……可看作项数为1、2、3……首项为3差分别为1、4、8……的数列.5﹣3=2=21、9﹣5=4=22、17﹣9=8=23……由此可以推出:第n项为2n+1.
【解答】解:由分析所总结的规律:
25+1
=32+1
=33(个)
答:五小时后细胞存活的个数是33个.
故选:B.
【点评】解答此题的关键是根据小时数(可看作项数),与分成成的活细胞(可看作项)之间的关系找出规律,然后根据规律可求出任何小时(整数)后活细胞的个数.
6.【分析】18﹣9=9,27﹣18=9,推测规律为:后一个数等于前一个数加9,以此计算,得出结果后,验证得数和其后面的数是否符合规律.
【解答】解:由分析可知:第四项为27+9=36
45﹣36=9
所以,找到的规律是正确的.
故选:B.
【点评】本题主要考查了数列中的规律,需要学生具有较好的数感和推理能力.
7.【分析】分析数据可得:第1个图形中小圆的个数为6;第2个图形中小圆的个数为10;第3个图形中小圆的个数为16;第4个图形中小圆的个数为24;则知第n个图形中小圆的个数为n(n+1)+4;由此把n=10代入计算即可.
【解答】解:10×11+4
=110+4
=114(个)
答:第10个图形中小圆的个数为114个.
故选:B.
【点评】本题是一道找规律的题目,这类题型在中考中经常出现.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,得出通项公式,从而解决问题.
8.【分析】观察已知的三个算式,可以发现,商的整数部分等于被除数的十位数字,小数循环部分的循环节是被除数十位上数字加1,以此作答.
【解答】解:由分析可知:61÷9的商,整数部分为6,小数循环节为6+1=7,
所以,61÷9=6.7777……
故选:C.
【点评】本题主要考查了“式”的规律,需要学生具有较好的数感.
二.填空题(共8小题)
9.【分析】根据题意,每次二人相差3+5=8(个)台阶,甲比乙高40个台阶,说明甲比乙多赢40÷8=5(次),其余次数二人输赢一样多.据此解答即可.
【解答】解:[25+40÷(5+3)]÷2
=[25+40÷8]÷2
=[25+5]÷2
=30÷2
=15(次)
答:甲胜了15次.
故答案为:15.
【点评】本题主要考查算术中的规律,关键根据题意找出二人每次胜负的台阶差.
10.【分析】(1)根据每次增加10求解;
(2)根据每次减少20求解.
【解答】解:(1)2,12,22,32,42,52.
(2)95,75,55,35,15.
故答案为:32,42,52;35,15.
【点评】通过观察,分析、归纳并发现其中的规律,并应用发现的规律解决问题是应该具备的基本能力.
11.【分析】根据积的变化规律:一个因数不变,另一个因数扩大或缩小多少倍(0除外),积也会随着扩大或缩小相同的倍数,据此解答即可得到答案.
【解答】解:因为
37×3=111
37×6=222
所以
37×9=333,
37×21=37×3×7=777,
故答案为:333,777.
【点评】此题主要考查的是积的变化规律的灵活应用,关键是根据已知算式找到规律.
12.【分析】从以上几题可以看出,用自然数从一位数开始,按从小到大自然数的顺序组成不同位数的数乘以8再加前面数的个位数,发现几位与8相乘结果还是几位,只是数从高位从大到小按自然数顺序排列,根据此规律就可填出得数.
【解答】解:1×8+1=9
12×8+2=98
123×8+3=987
1234×8+4=9876
……
123456789×8+9=987654321
故答案为:123456789,987654321.
【点评】解答本题的关键是根据已知数据找出规律,然后利用规律解题.
13.【分析】根据所给图示发现:这组积木的排列规律:第1个阶段积木个数:3×1=3(个);第2个阶段积木个数:3×2=6(个);第3个阶段积木个数:3×3=9(个)……第n个阶段积木个数为:3×n=3n(个).据此解答.
【解答】解:第1个阶段积木个数:3×1=3(个)
第2个阶段积木个数:3×2=6(个)
第3个阶段积木个数:3×3=9(个)
……
第n个阶段积木个数为:3×n=3n(个)
3n=171
n=57
答:要搭第n个阶段的积木的形状,一共需要积木3n个.现有积木数量171个,小红用上全部积木可以搭成第57阶段的立体图形.
故答案为:3n;57.
【点评】本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力.
14.【分析】根据所给图示可知:这组图形的排列规律:第一个图形白色小正方形的个数为1个,灰色小正方形的个数为6+2=8(个);第二个图形白色小正方形的个数为:2个,灰色小正方形的个数为:6+2+2=10(个);……第n个图形的白色小正方形的个数为n个,灰色小正方形的个数为(6+2n)个.据此解答.
【解答】解:第一个图形白色小正方形的个数为1个,灰色小正方形的个数为6+2=8(个)
第二个图形白色小正方形的个数为:2个,灰色小正方形的个数为:6+2+2=10(个)
……
第n个图形的白色小正方形的个数为n个,灰色小正方形的个数为(6+2n)个
所以第10个图形白色小正方形的个数为:10个
灰色小正方形的个数为:6+2×10=26(个)
答:第10个图形中有10个白色小正方形,26个灰色小正方形.
故答案为:10;26.
【点评】本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力.
15.【分析】由题意,可得规律:它第一次运走总量的;第二次运走余下的,即总量的(1﹣)×=;第三次运走余下的,即总量的:()×=;……第n次运走总量的:;第49次运走总量的:,则最后剩下:1﹣()=1﹣=
据此解答.
【解答】解:它第一次运走总量的;
第二次运走余下的,即总量的(1﹣)×=;
第三次运走余下的,即总量的:()×=;
……
第n次运走总量的:;
……
第49次运走总量的:,
则最后剩下:
1﹣()
=1﹣
=
答:当运走49次后,余下废料是总量的.
故答案为:
【点评】本题主要考查算术中的规律,关键运用分数的意义做题.
16.【分析】观察各式的分母,3=1×3,9=3×3,12=4×3,18=6×3,推测分母为3的连续倍数,根据此规律,将化为,化为,再观察各式的分子,1、3、5、7、9、11,为连续奇数,以此推断第十个数.
【解答】解:由分析可知,第十个的数分母为10×3=30,分子为2×10﹣1=19,
所以,第10个数为.
故答案为:.
【点评】本题主要考查了数列中的规律,先观察出分母的规律,然后改写部分项,再找出分子的规律,是本题解题的关键.
三.判断题(共5小题)
17.【分析】根据几个乘法算式找出的得数的规律,适用于所有具有同一特征算式的结果.如1×9=9、12×9=108、123×9=1107…如果第一个因数是1、12、123、1234…第二个因数都是9,其积所有数位的数字之和等于9,个位分别是9、8、7、6…十位都是0,其余数位上都是1.
【解答】解:如
1×9=9
12×9=108
123×9=1107
…
根据几个乘法算式找出的得数的规律,适用于所有具有同一特征算式的结果,这种说法正确.
故答案为:√.
【点评】只要几个乘法算式变化有一定的规律,其积也有一定规律.根据找出的规律可以写出符合这一规律所有算式的积.
18.【分析】根据图示,发现这组图形的规律:第一个点阵中点的个数:1个;第二个点阵中点的个数:1+4=5(个);第三个点阵中点的个数:1+4+4=9(个);……第n个点阵中点的个数:1+4(n﹣1)=(4n﹣3)(个).据此判断即可.
【解答】解:第一个点阵中点的个数:1个
第二个点阵中点的个数:1+4=5(个)
第三个点阵中点的个数:1+4+4=9(个)
……
第n个点阵中点的个数:1+4(n﹣1)=(4n﹣3)(个)
……
第五个点阵中点的个数:
4×5﹣3
=20﹣3
=17(个)
答:第五个点阵中点的个数是17个.所以原说法正确.
故答案为:√.
【点评】本题主要考查数与形结合的规律,关键根据图示发现这组图形的规律,并运用规律做题.
19.【分析】把分数化成小数,就会发现小数点后的数字是有规律的:=0.142857142857…,一直重复142857,所以小数点后的数字周期为6,2008÷6=334…4,每个周期第四个数为8,所以小数点后第2008位上的数字是8.
【解答】解:=1÷7=0.142857142857…,
一直重复142857,所以小数点后的数字周期为6.
2008÷6=334…4,
故小数点后第2008位上的数字是8.
故答案为:×.
【点评】考查了小数与分数的互化,算术中的规律,本题的关键是得到转化为小数,找出数字循环周期为6.
20.【分析】这组数每次递增15,所以用1415减去60,看能否被15整除即,如果能整除就是,否则不是;据此解答.
【解答】解:75﹣60=15,90﹣75=15,…,
所以这组数每次递增15,
(1415﹣60)÷15≈90.33,
所以,1415不是这组数中的数.
故答案为:√.
【点评】此题考查了数列的规律,关键是求出每次递增的数.
21.【分析】求2,4,6,8,10,……96,98,100的和即为求:2+4+6+8+10+…+100=?n=50,根据等差数列的求和公式完成计算.
【解答】解:2+4+6+8+10+…+100
=
=
=2550
所以原题计算正确.
故答案为:√.
【点评】根据等差数列求和公式进行计算,找出等差数列的公差,首项,尾项和项数是计算的关键.
四.应用题(共5小题)
22.【分析】1÷0.2=5,即1秒里面有5个0.2秒.第一张倒下后过0.2秒(1个0.2秒)会倒下2张、再过0.2秒(2个0.2秒)后会倒下4张、再过0.2秒(3个0.2秒)后会倒下8张、再过0.2秒(4个0.2秒)会倒下16张、再过0.2秒(5个0.2秒)会倒下32张.1、2、4、8、16、32.是公比为2的等比递增数列.最后把这些张数相加.
【解答】解:1÷0.2=5,即1秒里面有5个0.2秒
倒下第1张后
第1个0.2秒后会倒下2张
第2个0.2秒后会倒下4张
第3个0.2秒后会倒下8张
第4个0.2秒后会倒下16张
第5个0.2秒后会倒下32张
1+2+4+8+16+32
=1+2+(4+16)+(8+32)
=1+2+20+40
=63(张)
答:1秒钟内所倒下的骨牌数是63张.
【点评】这个数列项数是有限的,可以求出每次倒下的张数,然后再把倒下的总张数相加.如果项数较多要找规律解答.用小学知识只能这样解答.
23.【分析】15个盒子中的珠子从左到右是一个项数为15的等差数列,其中第8个盒子中的珠子数为中间项,根据等差数列的意义,与中间项相邻的左、右两项之和等于中间项,与中间项相隔1项的左、右两项之和也等于中间项……因此,这15项之和就是等于中间项乘中间项数.
【解答】解:24×15=360(颗)
答:这15个盒子中一共有360颗珠子.
【点评】解答此题的关键是明白:与中间项相邻的左、右两项之和等于中间项,与中间项相隔1项的左、右两项之和也等于中间项……
24.【分析】1+3═4=22
1+3+5═9=32
1+3+5+7═16=42
…
规律:[(首数+尾数)÷2]2=和;据此解答即可.
【解答】解:1+3═4=22
1+3+5═9=32
1+3+5+7═16=42
…
1+3+5+7+…+15═64=82
1+3+5+7+…+2017=1016064=10082
故答案为:4,22,9,32,16,42,64,82,1016064,10082.
【点评】解答此题的关键是观察所给出的算式,找出算式之间数与数的关系,得出规律,再根据规律解决问题.
25.【分析】摆1个六边形需要6根小棒,可以写作:5×1+1;摆2个需要11根小棒,可以写作:5×2+1;摆3个需要16根小棒,可以写成:5×3+1;…由此可以推理得出一般规律解答问题.
【解答】解:根据题干分析可得:摆1个六边形需要6根小棒,可以写作:5×1+1;
摆2个需要11根小棒,可以写作:5×2+1;
摆3个需要小棒:5×3+1=16;
摆n个需要小棒:5×n+1=5n+1;
当n=8时,5n+1=5×8+1=41;
答:图⑧一共需要41根小棒.
【点评】根据题干中已知的图形的排列特点及其数量关系,推理得出一般的结论进行解答,是此类问题的关键.
26.【分析】根据图示,发现其规律为:第一个图形中三角形个数:1个;第二个图形中三角形个数:1×4+1=5(个);第三个图形中三角形个数:2×4+1=9(个);第四个图形中三角形个数:3×4+1=13(个);第n个图形中三角形个数:(n﹣1)×4+1=(4n﹣3)(个),计算n的值即可.
【解答】解:第一个图形中三角形个数:1个;
第二个图形中三角形个数:1×4+1=5(个);
第三个图形中三角形个数:2×4+1=9(个);
第四个图形中三角形个数:3×4+1=13(个);
第n个图形中三角形个数:
(n﹣1)×4+1=(4n﹣3)(个)
4n﹣3=8057,n=2015.
答:n是第2015个图形.
【点评】本题主要考查数与形结合的规律,关键根据所给图示发现图示排列的规律,并运用规律做题.
五.操作题(共2小题)
27.【分析】根据图形,第一个图:2个,第二个图:4个; 第三个图:6个……所以,这组图形的规律是:图形的个数是连续的偶数个.据此作图即可.
【解答】解:如图:
【点评】本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力.
28.【分析】(1)3﹣1=2,6﹣3=3,10﹣6=4,相邻两个数的差依次是2,3,4,……,依次增加1;
(2)观察图中的星星的个数,分别是1、2、3、4……依次增加1;
(3)观察图中图形的个数,分别是10,8,6,4,……,依次减少2;
由此求解.
【解答】解:1.
2.
3.
【点评】关键是根据已知的数得出前后图形、数之间的变化关系的规律,然后再利用这个变化规律再回到问题中去解决问题.
