人教版8年级下册数学 19.2.2 一次函数 学案 (含答案)
文档属性
| 名称 | 人教版8年级下册数学 19.2.2 一次函数 学案 (含答案) | 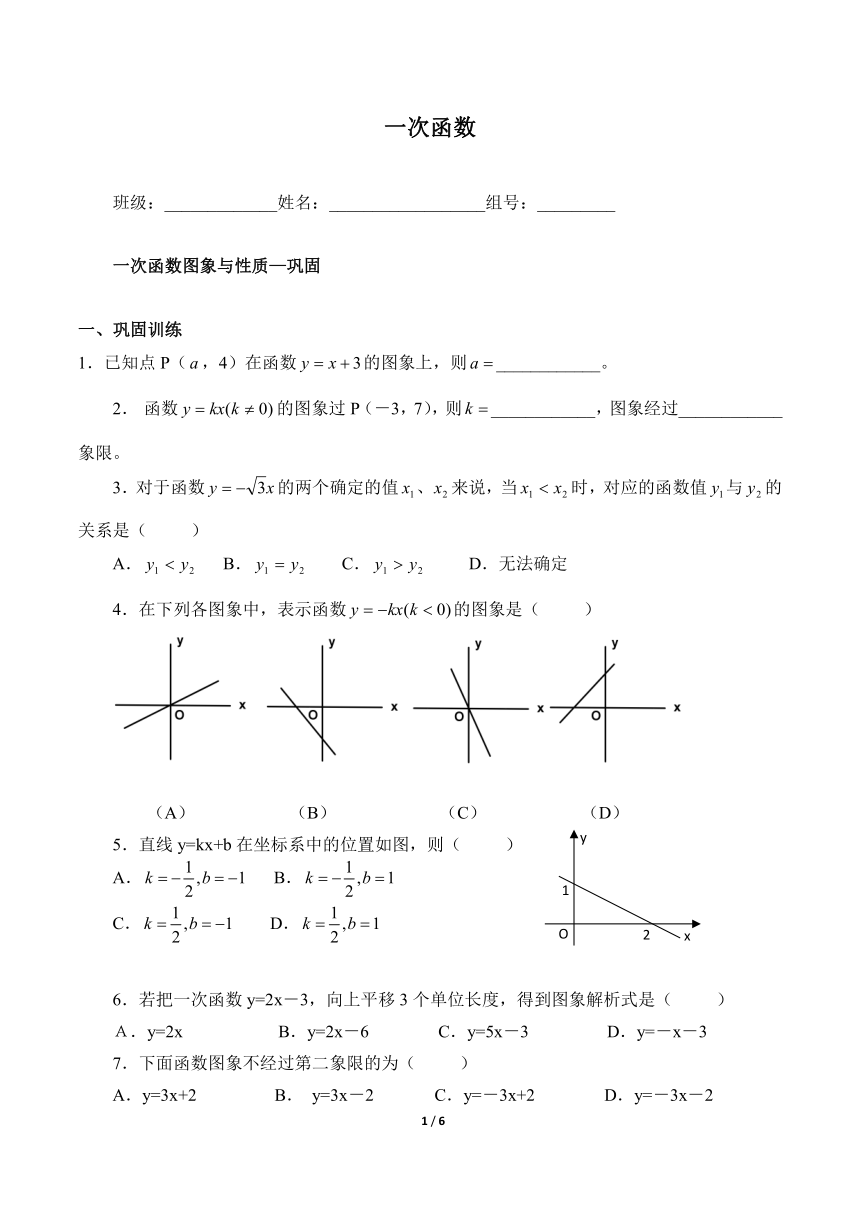 | |
| 格式 | doc | ||
| 文件大小 | 105.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-27 15:21:20 | ||
图片预览



文档简介
一次函数
班级:_____________姓名:__________________组号:_________
一次函数图象与性质—巩固
一、巩固训练
1.已知点P(,4)在函数的图象上,则____________。
2. 函数的图象过P(-3,7),则____________,图象经过____________象限。
3.对于函数的两个确定的值、来说,当时,对应的函数值与的关系是( )
A. B. C. D.无法确定
4.在下列各图象中,表示函数的图象是( )
(A) (B) (C) (D)
5.直线y=kx+b在坐标系中的位置如图,则( )
A. B.
C. D.
6.若把一次函数y=2x-3,向上平移3个单位长度,得到图象解析式是( )
A.y=2x B.y=2x-6 C.y=5x-3 D.y=-x-3
7.下面函数图象不经过第二象限的为( )
A.y=3x+2 B. y=3x-2 C.y=-3x+2 D.y=-3x-2
二、错题再现
1.已知一次函数y=kx+b的图象如图所示,则k,b的符号是( )
A.k>0,b>0 B.k>0,b<0
C.k<0,b>0 D.k<0,b<0
2.函数y=(m+1)x-(4m-3)的图象在第一、二、四象限,那么m的取值范是( )
A. B. C. D.
3.点M(-2,k)在直线y=2x+1上,求点M到x轴的距离d= 。
4.已知直线l与直线y=2x+1的交点的横坐标为2,与直线y=-x+2的交点的纵坐标为1,求直线l的函数关系式。
5.某医药研究所开发了一种新药,在实验药效时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(ug)随时间x(h)的变化情况如图所示。
(1)当成人按规定剂量服药后_______h,血液中含
药量最高,达每毫升______ug,接着逐步衰减;
(2)当成人按规定剂量服药后5h,血液中含药量为
每毫升________ug;
(3)求当x ≤ 2时,y与x之间的函数关系式;
(4)求当x ≥ 2时,y与x之间的函数关系式;
(5)若每毫升血液中含药3ug或3ug以上时,治疗疾病有效,求有效时间长度。
三、精练反馈
A组:
1.已知一次函数,函数的值随值的增大而增大,则的取值范围是 。
2.已知一次函数y=2x+4的图像经过点(m,8),则m=__________。
3.已知直线与轴,轴围成一个三角形,则这个三角形面积为 (平方单位)。
B组:
4.有甲、乙两家通迅公司,甲公司每月通话的收费标准如图所示;乙公司每月通话收费标准如表所示。
(1)观察图,甲公司用户月通话时间不超过100分钟时应付话费金额是______________元;甲公司用户通话100分钟以后,每分钟的通话费为_______________元;
月租费 通话费
25元 0.15元/分钟
(2)当通话时间为多少时,两家公司的收费是相同的?
【答案】
【巩固训练】
1.1
2.;二、四
3.C
4.A
5.B
6.A
7.B
【错题再现】
1.D
2.C
3.3
4.解:把x=2代入y=2x+1中的y=5
把y=1代入y=-x+2中的x=1
∴两交点的坐标为(2,5),(1,1)
设直线l的解析式为y=kx+b,代入得:
2k+b=5
K+b=1
解之得:k=4,b=-3
∴设直线l的解析式为y=4x-3
5.(1)2;6
(2)3
(3)设直线的解析式为,把代入得:
∴y与x之间的函数关系式
(4)设直线的解析式为,把,代入得:
∴y与x之间的函数关系式
(5)解:当x ≤ 2时,把代入得
当x ≤ 2时把代入得
∴有效的时间长度为5-1=4小时。
【精练反馈】
1.m>-2
2.2
3.18
4.(1)20;0.2
(2)解:设甲公司的直线解析式为,把
代入得:,
直线的解析式为
乙公司的解析式为,当两家公司的收费是相同时
解之得:,
答:当通话时间为500分钟时,两家公司的收费是相同。
O
x
y
1
2
y
x
甲公司
100
200
20
40
乙公司
6 / 6
班级:_____________姓名:__________________组号:_________
一次函数图象与性质—巩固
一、巩固训练
1.已知点P(,4)在函数的图象上,则____________。
2. 函数的图象过P(-3,7),则____________,图象经过____________象限。
3.对于函数的两个确定的值、来说,当时,对应的函数值与的关系是( )
A. B. C. D.无法确定
4.在下列各图象中,表示函数的图象是( )
(A) (B) (C) (D)
5.直线y=kx+b在坐标系中的位置如图,则( )
A. B.
C. D.
6.若把一次函数y=2x-3,向上平移3个单位长度,得到图象解析式是( )
A.y=2x B.y=2x-6 C.y=5x-3 D.y=-x-3
7.下面函数图象不经过第二象限的为( )
A.y=3x+2 B. y=3x-2 C.y=-3x+2 D.y=-3x-2
二、错题再现
1.已知一次函数y=kx+b的图象如图所示,则k,b的符号是( )
A.k>0,b>0 B.k>0,b<0
C.k<0,b>0 D.k<0,b<0
2.函数y=(m+1)x-(4m-3)的图象在第一、二、四象限,那么m的取值范是( )
A. B. C. D.
3.点M(-2,k)在直线y=2x+1上,求点M到x轴的距离d= 。
4.已知直线l与直线y=2x+1的交点的横坐标为2,与直线y=-x+2的交点的纵坐标为1,求直线l的函数关系式。
5.某医药研究所开发了一种新药,在实验药效时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(ug)随时间x(h)的变化情况如图所示。
(1)当成人按规定剂量服药后_______h,血液中含
药量最高,达每毫升______ug,接着逐步衰减;
(2)当成人按规定剂量服药后5h,血液中含药量为
每毫升________ug;
(3)求当x ≤ 2时,y与x之间的函数关系式;
(4)求当x ≥ 2时,y与x之间的函数关系式;
(5)若每毫升血液中含药3ug或3ug以上时,治疗疾病有效,求有效时间长度。
三、精练反馈
A组:
1.已知一次函数,函数的值随值的增大而增大,则的取值范围是 。
2.已知一次函数y=2x+4的图像经过点(m,8),则m=__________。
3.已知直线与轴,轴围成一个三角形,则这个三角形面积为 (平方单位)。
B组:
4.有甲、乙两家通迅公司,甲公司每月通话的收费标准如图所示;乙公司每月通话收费标准如表所示。
(1)观察图,甲公司用户月通话时间不超过100分钟时应付话费金额是______________元;甲公司用户通话100分钟以后,每分钟的通话费为_______________元;
月租费 通话费
25元 0.15元/分钟
(2)当通话时间为多少时,两家公司的收费是相同的?
【答案】
【巩固训练】
1.1
2.;二、四
3.C
4.A
5.B
6.A
7.B
【错题再现】
1.D
2.C
3.3
4.解:把x=2代入y=2x+1中的y=5
把y=1代入y=-x+2中的x=1
∴两交点的坐标为(2,5),(1,1)
设直线l的解析式为y=kx+b,代入得:
2k+b=5
K+b=1
解之得:k=4,b=-3
∴设直线l的解析式为y=4x-3
5.(1)2;6
(2)3
(3)设直线的解析式为,把代入得:
∴y与x之间的函数关系式
(4)设直线的解析式为,把,代入得:
∴y与x之间的函数关系式
(5)解:当x ≤ 2时,把代入得
当x ≤ 2时把代入得
∴有效的时间长度为5-1=4小时。
【精练反馈】
1.m>-2
2.2
3.18
4.(1)20;0.2
(2)解:设甲公司的直线解析式为,把
代入得:,
直线的解析式为
乙公司的解析式为,当两家公司的收费是相同时
解之得:,
答:当通话时间为500分钟时,两家公司的收费是相同。
O
x
y
1
2
y
x
甲公司
100
200
20
40
乙公司
6 / 6
