人教版8年级下册数学 19.3 课题学习 选择方案 学案(含答案)
文档属性
| 名称 | 人教版8年级下册数学 19.3 课题学习 选择方案 学案(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 117.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-27 16:17:27 | ||
图片预览


文档简介
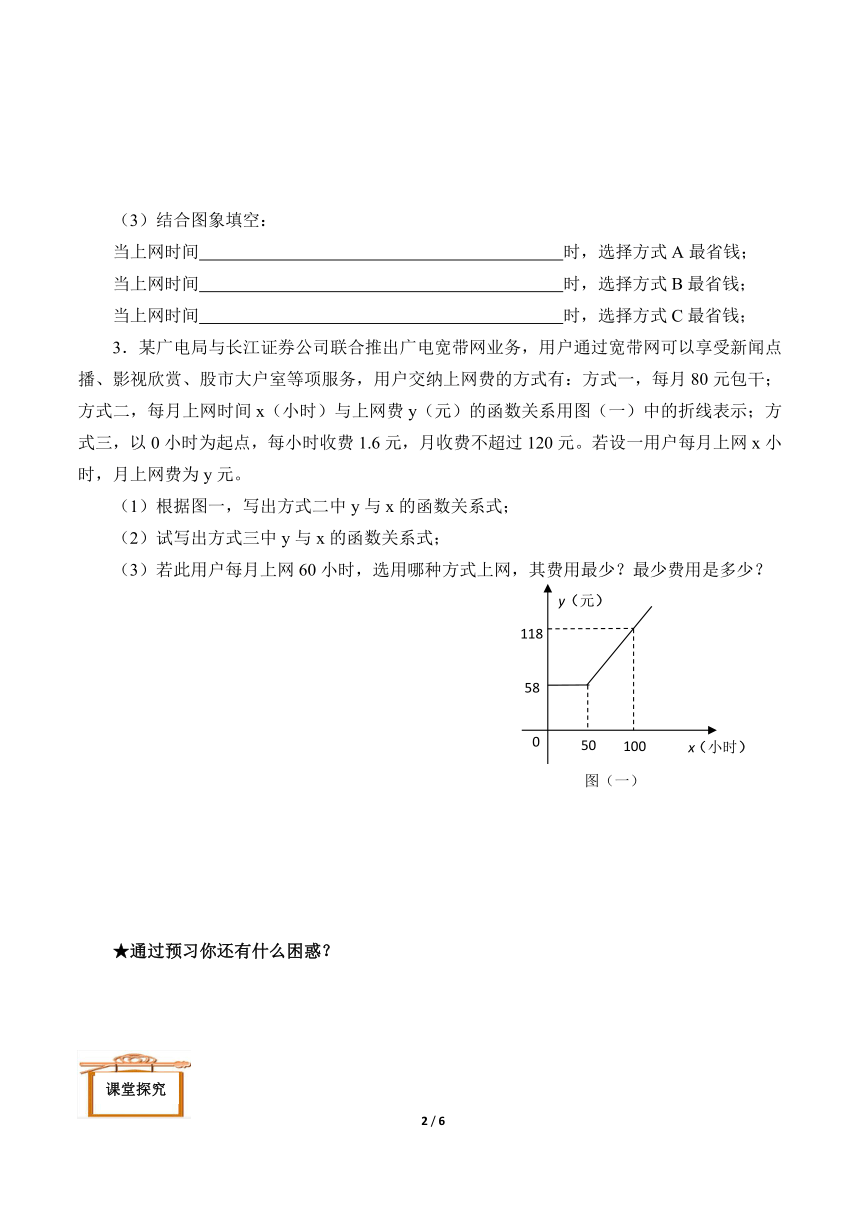
课题学习 选择方案
班级:_____________姓名:__________________组号:_________
第一课时
1.举例说明一次函数与一元一次方程,一元一次不等式之间的关系。
2.认真阅读P102的问题1,回答以下问题:
(1)设月上网时间为h,分别列出A,B,C三种收费方式,关于上网时间的函数关系式。
(2)在上图中画出它的图象。
(3)结合图象填空:
当上网时间 时,选择方式A最省钱;
当上网时间 时,选择方式B最省钱;
当上网时间 时,选择方式C最省钱;
3.某广电局与长江证券公司联合推出广电宽带网业务,用户通过宽带网可以享受新闻点播、影视欣赏、股市大户室等项服务,用户交纳上网费的方式有:方式一,每月80元包干;方式二,每月上网时间x(小时)与上网费y(元)的函数关系用图(一)中的折线表示;方式三,以0小时为起点,每小时收费1.6元,月收费不超过120元。若设一用户每月上网x小时,月上网费为y元。
(1)根据图一,写出方式二中y与x的函数关系式;
(2)试写出方式三中y与x的函数关系式;
(3)若此用户每月上网60小时,选用哪种方式上网,其费用最少?最少费用是多少?
★通过预习你还有什么困惑?
一、课堂活动、记录
如何从实际问题构建一次函数模型进行解决问题?
二、精练反馈
1.甲、乙两商场春节期间都进行让利酬宾活动。其中,甲商场对一次购物中超过200元后的价格部分打7折,如图所示,表示甲商场在让利方式下关于的函数图象,(单位:元)表示商品原价,(单位:元)表示购物金额。若乙商场所有商品按8折出售,请在同一坐标系下画出,乙商场在让利方式下关于的函数图像,并说明如何选择这两家商场购物更省钱。
三、课堂小结
1.如何从实际问题构建一次函数模型。
2.你的其他收获。
四、拓展延伸(选做题)
1.在购买某场足球赛门票时,设购买门票数为(张),总费用为(元)。现有两种购买方案:
方案一:若单位赞助广告费10000元,则该单位所购门票的价格为每张60元;
(总费用=广告赞助费+门票费)
方案二:购买门票方式如图所示。
解答下列问题:
(1)方案一中,与的函数关系式为 。
方案二中,当0≤≤100时,与的函数关系式为 ;
当>100时,与的函数关系式为 。
(2)如果购买本场足球赛门票超过100张,你将选择哪一种方案,使总费用最省?请说明理由;
(3)甲、乙两单位分别采用方案一、方案二购买本场足球赛门票共700张,花去总费用计58000元,求甲、乙两单位各购买门票多少张。
【答案】
【学前准备】
1.略
2.(1)即
同理: y3=120
(2)略
(3);;
3.解:(1)当0≤x≤50时,y=58,
当50≤x≤100时,y=1.2x-2;
(2)当0≤x≤75时,根据题意可得:y=1.6x;
(3)当用户每月上网60小时,上网的总费用应该是:
方案一:由于是包月,因此是80元;
方案二:y=1.2×60-2=70元;
方案三:y=1.6×60=96元。
因此方案二最省钱。
【课堂探究】
课堂活动、记录
略
精练反馈
1.解:乙商场的让利方式关于的函数图象如图所示
∵y乙=0.8x y甲=200+0.7(x-200)=0.7x+60
令,得x=600
当x>600元时,选择甲
当x=600元时,甲乙一样
当x<600元时,选择乙
课堂小结
略
拓展延伸(选做题)
解:(1)方案一:y=60x+10000 ;
当0≤x≤100时,y=100x ;
当x>100时,y=80x+2000.
(2)因为方案一y与x的函数关系式为y=60x+10000,
∵x>100,方案二的y与x的函数关系式为y=80x+2000;
当60x+10000>80x+2000时,即x<400时,选方案二进行购买,
当60x+10000=80x+2000时,即x=400时,两种方案都可以,
当60x+10000<80x+2000时,即x>400时,选方案一进行购买;
(3)设甲、乙单位购买本次足球赛门票数分别为a张、b张;
∵甲、乙单位分别采用方案一和方案二购买本次足球比赛门票,
∴乙公司购买本次足球赛门票有两种情况:b≤100或b>100
当b≤100时,乙公司购买本次足球赛门票费为100b,
则
解得不符合题意,舍去
当b>100时,乙公司购买本次足球赛门票费为80b+2000
则
解得符合题意
答:甲、乙单位购买本次足球赛门票分别为500张、200张
学前准备
0
50
100
x(小时)
y(元)
118
58
图(一)
课堂探究
10000
14000
100
150
O
x(张)
y(元)
6 / 6
班级:_____________姓名:__________________组号:_________
第一课时
1.举例说明一次函数与一元一次方程,一元一次不等式之间的关系。
2.认真阅读P102的问题1,回答以下问题:
(1)设月上网时间为h,分别列出A,B,C三种收费方式,关于上网时间的函数关系式。
(2)在上图中画出它的图象。
(3)结合图象填空:
当上网时间 时,选择方式A最省钱;
当上网时间 时,选择方式B最省钱;
当上网时间 时,选择方式C最省钱;
3.某广电局与长江证券公司联合推出广电宽带网业务,用户通过宽带网可以享受新闻点播、影视欣赏、股市大户室等项服务,用户交纳上网费的方式有:方式一,每月80元包干;方式二,每月上网时间x(小时)与上网费y(元)的函数关系用图(一)中的折线表示;方式三,以0小时为起点,每小时收费1.6元,月收费不超过120元。若设一用户每月上网x小时,月上网费为y元。
(1)根据图一,写出方式二中y与x的函数关系式;
(2)试写出方式三中y与x的函数关系式;
(3)若此用户每月上网60小时,选用哪种方式上网,其费用最少?最少费用是多少?
★通过预习你还有什么困惑?
一、课堂活动、记录
如何从实际问题构建一次函数模型进行解决问题?
二、精练反馈
1.甲、乙两商场春节期间都进行让利酬宾活动。其中,甲商场对一次购物中超过200元后的价格部分打7折,如图所示,表示甲商场在让利方式下关于的函数图象,(单位:元)表示商品原价,(单位:元)表示购物金额。若乙商场所有商品按8折出售,请在同一坐标系下画出,乙商场在让利方式下关于的函数图像,并说明如何选择这两家商场购物更省钱。
三、课堂小结
1.如何从实际问题构建一次函数模型。
2.你的其他收获。
四、拓展延伸(选做题)
1.在购买某场足球赛门票时,设购买门票数为(张),总费用为(元)。现有两种购买方案:
方案一:若单位赞助广告费10000元,则该单位所购门票的价格为每张60元;
(总费用=广告赞助费+门票费)
方案二:购买门票方式如图所示。
解答下列问题:
(1)方案一中,与的函数关系式为 。
方案二中,当0≤≤100时,与的函数关系式为 ;
当>100时,与的函数关系式为 。
(2)如果购买本场足球赛门票超过100张,你将选择哪一种方案,使总费用最省?请说明理由;
(3)甲、乙两单位分别采用方案一、方案二购买本场足球赛门票共700张,花去总费用计58000元,求甲、乙两单位各购买门票多少张。
【答案】
【学前准备】
1.略
2.(1)即
同理: y3=120
(2)略
(3);;
3.解:(1)当0≤x≤50时,y=58,
当50≤x≤100时,y=1.2x-2;
(2)当0≤x≤75时,根据题意可得:y=1.6x;
(3)当用户每月上网60小时,上网的总费用应该是:
方案一:由于是包月,因此是80元;
方案二:y=1.2×60-2=70元;
方案三:y=1.6×60=96元。
因此方案二最省钱。
【课堂探究】
课堂活动、记录
略
精练反馈
1.解:乙商场的让利方式关于的函数图象如图所示
∵y乙=0.8x y甲=200+0.7(x-200)=0.7x+60
令,得x=600
当x>600元时,选择甲
当x=600元时,甲乙一样
当x<600元时,选择乙
课堂小结
略
拓展延伸(选做题)
解:(1)方案一:y=60x+10000 ;
当0≤x≤100时,y=100x ;
当x>100时,y=80x+2000.
(2)因为方案一y与x的函数关系式为y=60x+10000,
∵x>100,方案二的y与x的函数关系式为y=80x+2000;
当60x+10000>80x+2000时,即x<400时,选方案二进行购买,
当60x+10000=80x+2000时,即x=400时,两种方案都可以,
当60x+10000<80x+2000时,即x>400时,选方案一进行购买;
(3)设甲、乙单位购买本次足球赛门票数分别为a张、b张;
∵甲、乙单位分别采用方案一和方案二购买本次足球比赛门票,
∴乙公司购买本次足球赛门票有两种情况:b≤100或b>100
当b≤100时,乙公司购买本次足球赛门票费为100b,
则
解得不符合题意,舍去
当b>100时,乙公司购买本次足球赛门票费为80b+2000
则
解得符合题意
答:甲、乙单位购买本次足球赛门票分别为500张、200张
学前准备
0
50
100
x(小时)
y(元)
118
58
图(一)
课堂探究
10000
14000
100
150
O
x(张)
y(元)
6 / 6
