人教版8年级下册数学 19.3 课题学习 选择方案 课时练(含答案)
文档属性
| 名称 | 人教版8年级下册数学 19.3 课题学习 选择方案 课时练(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 251.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-27 00:00:00 | ||
图片预览


文档简介
《19.3课题学习 选择方案》课时练
一、单选题
1.明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )
A.300m2 B.150m2 C.330m2 D.450m2
2.如图,点B,C分别在直线和直线上,A,D是x轴上的两点,若四边形ABCD是长方形,且,则k的值是( )
A. B. C. D.
3.张师傅驾车从甲地到乙地,两地相距500千米,汽车出发前油箱有油25升,途中加油若干升,加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.以下说法错误的是
A.加油前油箱中剩余油量y(升)与行驶时间t(小时)的函数关系是y=﹣8t+25
B.途中加油21升
C.汽车加油后还可行驶4小时
D.汽车到达乙地时油箱中还余油6升
4.某种品牌的同一种洗衣粉有A,B,C三种袋装包装,每袋分别装有400克、300克、200克的洗衣粉,售价分别为3.5元、2.8元、1.9元.A,B,C三种包装的洗衣粉,每袋的包装费用(含包装袋成本)分别为0.8元、0.6元、0.5元.厂家销售A,B,C三种包装的洗衣粉各1 200千克,获得利润最大的是( )
A.A种包装的洗衣粉 B.B种包装的洗衣粉
C.C种包装的洗衣粉 D.三种包装的都相同
5.如图是邻居张大爷去公园锻炼及原路返回时离家的距离y(千米)与时间t(分钟)之间的函数图象,根据图象信息,下列说法不正确的是( )
A.张大爷去时所用的时间多于回家的时间.
B.张大爷在公园锻炼了40分钟
C.张大爷去是走上坡路,回家时走下坡路
D.张大爷去时的速度比回家时的速度慢
6.一个生产、装箱流水线,生产前没有积压产品,开始的3小时只生产,3小时后安排装箱(生产没有停止),8小时后生产停止只安排装箱,第13小时时生产流水线刚好没有积压产品,已知流水线的生产、装箱的速度保持不变,流水线上积压产品(没有装箱产品)y(吨)与流水线工作时间x(小时)之间的函数关系如图所示,则在整个过程中,积压产品最多为( )
A.9.5吨 B.10吨 C.11吨 D.12吨
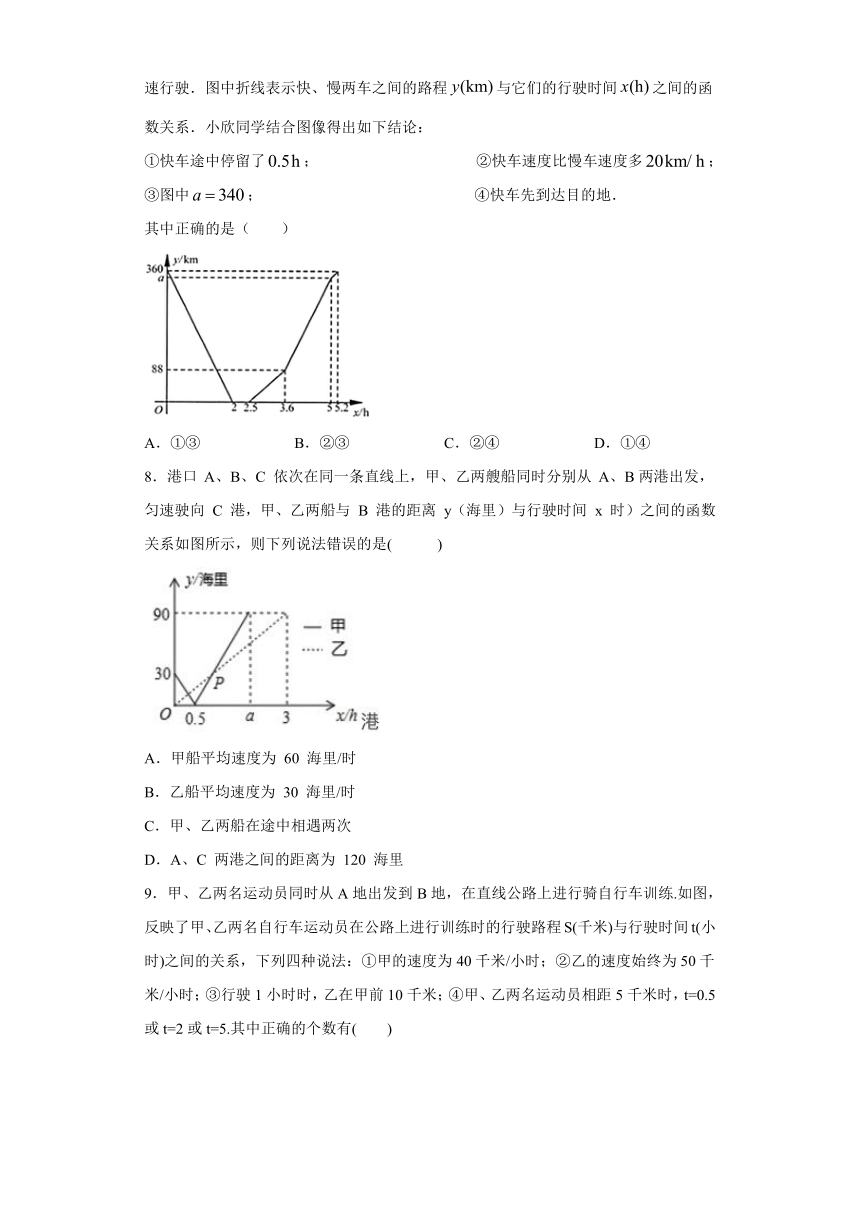
7.快车从甲地驶往乙地,慢车从乙地驶往甲地,两车同时出发并且在同一条公路上匀速行驶.图中折线表示快、慢两车之间的路程与它们的行驶时间之间的函数关系.小欣同学结合图像得出如下结论:
①快车途中停留了; ②快车速度比慢车速度多;
③图中; ④快车先到达目的地.
其中正确的是( )
A.①③ B.②③ C.②④ D.①④
8.港口 A、B、C 依次在同一条直线上,甲、乙两艘船同时分别从 A、B两港出发,匀速驶向 C 港,甲、乙两船与 B 港的距离 y(海里)与行驶时间 x 时)之间的函数关系如图所示,则下列说法错误的是( )
A.甲船平均速度为 60 海里/时
B.乙船平均速度为 30 海里/时
C.甲、乙两船在途中相遇两次
D.A、C 两港之间的距离为 120 海里
9.甲、乙两名运动员同时从A地出发到B地,在直线公路上进行骑自行车训练.如图,反映了甲、乙两名自行车运动员在公路上进行训练时的行驶路程S(千米)与行驶时间t(小时)之间的关系,下列四种说法:①甲的速度为40千米/小时;②乙的速度始终为50千米/小时;③行驶1小时时,乙在甲前10千米;④甲、乙两名运动员相距5千米时,t=0.5或t=2或t=5.其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
10.甲、乙两船沿直线航道AC匀速航行.甲船从起点A出发,同时乙船从航道AC中途的点B出发,向终点C航行.设t小时后甲、乙两船与B处的距离分别为d1,d2,则d1,d2与t的函数关系如图.下列说法:
①乙船的速度是40千米/时;
②甲船航行1小时到达B处;
③甲、乙两船航行0.6小时相遇;
④甲、乙两船的距离不小于10千米的时间段是0≤t≤2.5.其中正确的说法的是( )
A.①② B.①②③ C.①②④ D.①②③④
二、填空题
11.小明从家步行到学校,图中的折线反映了小明从家步行到学校所走的路程(米)与时间(分钟)的函数关系,根据图像提供的信息,线段表示的函数解析式是_________.
12.油箱中有油20升,油从管道中匀速流出,100分钟流完.匀速流出的过程,油箱中剩油量y(升)与流出的时间x(分钟)之间的函数关系式是_____(并写出自变量取值范围).
13.在锅中倒入了一些油,用煤气灶均匀加热,每隔20秒测一次油温,得到下表:
时间x(秒) 0 20 40 60 …
油温y(℃) 10 50 90 130 …
加热110秒时,油刚好沸腾了,估计这种油沸点的温度为_____℃.
14.本年度某单位常有集体外出学习活动,因此准备与出租车公司签订租车协议.现有甲、乙两家出租车公司供选择.设每月行驶千米,应付给甲公司元,应付给乙公司元,、分别与之间的函数关系如图所示,若这个单位估计每月需要行驶的路程为3500千米,那么为了省钱,这个单位应租__________公司.
15.我市认真落实国家“精准扶贫”政策,计划在对口帮扶的贫困县种植甲、乙两种火龙果共100亩,根据市场调查,甲、乙两种火龙果每亩的种植成本分别为0.9万元、1.1万元,每亩的销售额分别为2万元、2.5万元,如果要求种植成本不少于98万元,但不超过100万元,且所有火龙果能全部售出,则该县在此项目中获得的最大利润是_____万元.(利润=销售额﹣种植成本)
三、解答题
16.某景区售票处规定:非节假日的票价打a折售票;节假日根据团队人数x(人)实行分段售票;若x≤10,则按原展价购买;若x>10,则其中10人按原票价购买,超过部分的按原那价打b折购买.某旅行社带团到该景区游览,设在非节假日的购票款为y1元,在节假日的购票款为y2元,y1、y2与x之间的函数图象如图所示.
(1)观察图象可知:a=_______,b=_______;
(2)当x>10时,求y2与x之间的函数表达式;
(3)该旅行社在今年5月1日带甲团与5月10日(非节假日)带乙团到该景区游览,两团合计50人,共付门票款3120元,求甲团人数与乙团人数.
17.兰州市居民用电现有两种用电收费方式:
智能分时电表 普通电表
峰时(8:00﹣22:00) 谷时(22:00﹣次日8:00) 电价0.51/千瓦时
电价0.76元/千万时 电价0.26元/千瓦时
设某家庭某月用电总量为x千瓦时,其中谷时用电60千瓦时,则峰时用电(x﹣60)千瓦时,智能分时电表计价时的总价为为y1(元),普通电表计价时的总价为y2(元).请分别写出两种电表计价时的总价与用电总量之间的函数关系式.
18.某水果店每天都会进一些草莓销售.在一周销售过程中他发现每天的销售量y(单位:千克)会随售价x(单位:元/千克)的变化而变化,部分数据记录如表:
售价x(单位:元/千克) 30 25 20
每天销售量y(单位:千克) 5 45 85
如果已知草莓每天销量y与售价x(14<x<30.625)满足一次函数关系.
(1)请根据表格中数据求出这个一次函数关系式;
(2)如果进价为14元/千克,请判断售价分别定为20元/千克和25元/千克时,哪个的销售利润更高?
参考答案
1.B
2.B
3.C
4.B
5.B
6.D
7.B
8.C
9.B
10.C
11..
12.y=20﹣x(0≤x≤100)
13.230
14.甲
15.125
16.(1)6,8;(2)y2=64x+160 (x>10),(3)甲团有35人,乙团有15人.
17.,.
18.(1)y=﹣8x+245;(2)当售价为20元/千克时的销售利润更高
一、单选题
1.明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )
A.300m2 B.150m2 C.330m2 D.450m2
2.如图,点B,C分别在直线和直线上,A,D是x轴上的两点,若四边形ABCD是长方形,且,则k的值是( )
A. B. C. D.
3.张师傅驾车从甲地到乙地,两地相距500千米,汽车出发前油箱有油25升,途中加油若干升,加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.以下说法错误的是
A.加油前油箱中剩余油量y(升)与行驶时间t(小时)的函数关系是y=﹣8t+25
B.途中加油21升
C.汽车加油后还可行驶4小时
D.汽车到达乙地时油箱中还余油6升
4.某种品牌的同一种洗衣粉有A,B,C三种袋装包装,每袋分别装有400克、300克、200克的洗衣粉,售价分别为3.5元、2.8元、1.9元.A,B,C三种包装的洗衣粉,每袋的包装费用(含包装袋成本)分别为0.8元、0.6元、0.5元.厂家销售A,B,C三种包装的洗衣粉各1 200千克,获得利润最大的是( )
A.A种包装的洗衣粉 B.B种包装的洗衣粉
C.C种包装的洗衣粉 D.三种包装的都相同
5.如图是邻居张大爷去公园锻炼及原路返回时离家的距离y(千米)与时间t(分钟)之间的函数图象,根据图象信息,下列说法不正确的是( )
A.张大爷去时所用的时间多于回家的时间.
B.张大爷在公园锻炼了40分钟
C.张大爷去是走上坡路,回家时走下坡路
D.张大爷去时的速度比回家时的速度慢
6.一个生产、装箱流水线,生产前没有积压产品,开始的3小时只生产,3小时后安排装箱(生产没有停止),8小时后生产停止只安排装箱,第13小时时生产流水线刚好没有积压产品,已知流水线的生产、装箱的速度保持不变,流水线上积压产品(没有装箱产品)y(吨)与流水线工作时间x(小时)之间的函数关系如图所示,则在整个过程中,积压产品最多为( )
A.9.5吨 B.10吨 C.11吨 D.12吨
7.快车从甲地驶往乙地,慢车从乙地驶往甲地,两车同时出发并且在同一条公路上匀速行驶.图中折线表示快、慢两车之间的路程与它们的行驶时间之间的函数关系.小欣同学结合图像得出如下结论:
①快车途中停留了; ②快车速度比慢车速度多;
③图中; ④快车先到达目的地.
其中正确的是( )
A.①③ B.②③ C.②④ D.①④
8.港口 A、B、C 依次在同一条直线上,甲、乙两艘船同时分别从 A、B两港出发,匀速驶向 C 港,甲、乙两船与 B 港的距离 y(海里)与行驶时间 x 时)之间的函数关系如图所示,则下列说法错误的是( )
A.甲船平均速度为 60 海里/时
B.乙船平均速度为 30 海里/时
C.甲、乙两船在途中相遇两次
D.A、C 两港之间的距离为 120 海里
9.甲、乙两名运动员同时从A地出发到B地,在直线公路上进行骑自行车训练.如图,反映了甲、乙两名自行车运动员在公路上进行训练时的行驶路程S(千米)与行驶时间t(小时)之间的关系,下列四种说法:①甲的速度为40千米/小时;②乙的速度始终为50千米/小时;③行驶1小时时,乙在甲前10千米;④甲、乙两名运动员相距5千米时,t=0.5或t=2或t=5.其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
10.甲、乙两船沿直线航道AC匀速航行.甲船从起点A出发,同时乙船从航道AC中途的点B出发,向终点C航行.设t小时后甲、乙两船与B处的距离分别为d1,d2,则d1,d2与t的函数关系如图.下列说法:
①乙船的速度是40千米/时;
②甲船航行1小时到达B处;
③甲、乙两船航行0.6小时相遇;
④甲、乙两船的距离不小于10千米的时间段是0≤t≤2.5.其中正确的说法的是( )
A.①② B.①②③ C.①②④ D.①②③④
二、填空题
11.小明从家步行到学校,图中的折线反映了小明从家步行到学校所走的路程(米)与时间(分钟)的函数关系,根据图像提供的信息,线段表示的函数解析式是_________.
12.油箱中有油20升,油从管道中匀速流出,100分钟流完.匀速流出的过程,油箱中剩油量y(升)与流出的时间x(分钟)之间的函数关系式是_____(并写出自变量取值范围).
13.在锅中倒入了一些油,用煤气灶均匀加热,每隔20秒测一次油温,得到下表:
时间x(秒) 0 20 40 60 …
油温y(℃) 10 50 90 130 …
加热110秒时,油刚好沸腾了,估计这种油沸点的温度为_____℃.
14.本年度某单位常有集体外出学习活动,因此准备与出租车公司签订租车协议.现有甲、乙两家出租车公司供选择.设每月行驶千米,应付给甲公司元,应付给乙公司元,、分别与之间的函数关系如图所示,若这个单位估计每月需要行驶的路程为3500千米,那么为了省钱,这个单位应租__________公司.
15.我市认真落实国家“精准扶贫”政策,计划在对口帮扶的贫困县种植甲、乙两种火龙果共100亩,根据市场调查,甲、乙两种火龙果每亩的种植成本分别为0.9万元、1.1万元,每亩的销售额分别为2万元、2.5万元,如果要求种植成本不少于98万元,但不超过100万元,且所有火龙果能全部售出,则该县在此项目中获得的最大利润是_____万元.(利润=销售额﹣种植成本)
三、解答题
16.某景区售票处规定:非节假日的票价打a折售票;节假日根据团队人数x(人)实行分段售票;若x≤10,则按原展价购买;若x>10,则其中10人按原票价购买,超过部分的按原那价打b折购买.某旅行社带团到该景区游览,设在非节假日的购票款为y1元,在节假日的购票款为y2元,y1、y2与x之间的函数图象如图所示.
(1)观察图象可知:a=_______,b=_______;
(2)当x>10时,求y2与x之间的函数表达式;
(3)该旅行社在今年5月1日带甲团与5月10日(非节假日)带乙团到该景区游览,两团合计50人,共付门票款3120元,求甲团人数与乙团人数.
17.兰州市居民用电现有两种用电收费方式:
智能分时电表 普通电表
峰时(8:00﹣22:00) 谷时(22:00﹣次日8:00) 电价0.51/千瓦时
电价0.76元/千万时 电价0.26元/千瓦时
设某家庭某月用电总量为x千瓦时,其中谷时用电60千瓦时,则峰时用电(x﹣60)千瓦时,智能分时电表计价时的总价为为y1(元),普通电表计价时的总价为y2(元).请分别写出两种电表计价时的总价与用电总量之间的函数关系式.
18.某水果店每天都会进一些草莓销售.在一周销售过程中他发现每天的销售量y(单位:千克)会随售价x(单位:元/千克)的变化而变化,部分数据记录如表:
售价x(单位:元/千克) 30 25 20
每天销售量y(单位:千克) 5 45 85
如果已知草莓每天销量y与售价x(14<x<30.625)满足一次函数关系.
(1)请根据表格中数据求出这个一次函数关系式;
(2)如果进价为14元/千克,请判断售价分别定为20元/千克和25元/千克时,哪个的销售利润更高?
参考答案
1.B
2.B
3.C
4.B
5.B
6.D
7.B
8.C
9.B
10.C
11..
12.y=20﹣x(0≤x≤100)
13.230
14.甲
15.125
16.(1)6,8;(2)y2=64x+160 (x>10),(3)甲团有35人,乙团有15人.
17.,.
18.(1)y=﹣8x+245;(2)当售价为20元/千克时的销售利润更高
